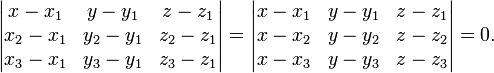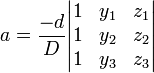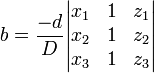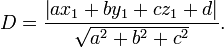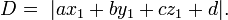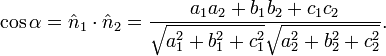Plane (geometria)

Dois planos que se cruzam no espaço tridimensional

Em matemática , um avião é uma bidimensional colector ou superfície que é perfeitamente plana. Informalmente, que pode ser pensado como um infinitamente grande e infinitamente fina folha orientada em alguns espaço. Formalmente, é um espaço afim de dimensão dois.

Ao trabalhar no espaço euclidiano bidimensional, o artigo definido é usado, o avião, para se referir a todo o espaço. Muitas funções fundamentais na geometria , trigonometria , e de gráficos são realizadas no espaço bidimensional, ou por outras palavras, no plano. Um monte de matemática pode ser e tem sido executado no plano, nomeadamente nas áreas de geometria , trigonometria , teoria dos grafos e gráficos.

Geometria euclidiana

No espaço euclidiano um avião é uma superfície de tal modo que, dado qualquer dois distintos pontos na superfície, a superfície também contém a única linha recta , que passa através daqueles pontos.

A estrutura fundamental de dois aviões deste tipo será sempre o mesmo. Em matemática isto é descrito como equivalência topológica . Informalmente, porém, isso significa que nenhum dois aviões a mesma aparência.

Um avião pode ser determinada de forma única por qualquer um dos seguintes conjuntos de () objetos:

• três pontos não colineares (isto é, não encontra-se na mesma linha )
• uma linha e um ponto não na linha
• duas linhas com um ponto de intersecção
• duas linhas paralelas

Planes embutidos em R ³

Esta seção é especificamente relacionado com aviões incorporados em três dimensões: especificamente, em ℝ ^3.

Propriedades

No espaço euclidiano tridimensional, podemos explorar os seguintes fatos que não se sustentam, nas dimensões superiores:

• Dois planos são ou paralelo ou se cruzam em uma linha.
• Uma linha ou é paralelo a um plano que intersecta ou em um ponto único ou está contido no plano.
• Duas linhas perpendicular ao plano da mesma deve ser paralelos um ao outro.
• Dois planos perpendiculares à mesma linha devem ser paralelos um ao outro.

Definem um plano com um ponto e um vetor normal

Em um espaço tridimensional, outra importante forma de definir um plano é especificando um ponto e uma vector normal ao plano.

Deixar ser o ponto que desejamos coincidir com o plano, e deixá- ser um vetor normal diferente de zero em relação ao plano. O plano desejado é o conjunto de todos os pontos 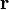tal que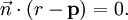

Se escrevermos 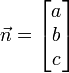, 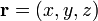e d como o produto de ponto 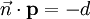, Então o plano 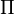é determinada pela condição 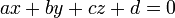, Onde a, b, c e d são números reais e a, b, c e não sejam todos zero.

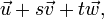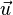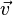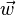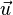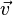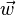Alternativamente, um avião pode ser descrito parametricamente como o conjunto de todos os pontos da forma onde s e faixa de t sobre todos os números reais, e , e são dadas vetores que definem o avião. aponta a partir da origem para um ponto arbitrário no avião, e e pode ser visualizada como a partir de 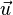e apontando em direcções diferentes ao longo do plano. 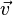e 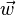pode, mas não tem que ser perpendicular (mas eles não podem ser collinear).

Definir um plano através de três pontos

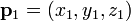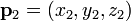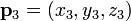• O plano que passa por três pontos , e pode ser definido como o conjunto de todos os pontos (x, y, z) que satisfazem os seguintes determinantes equações:

• Para descrever o plano como uma equação na forma 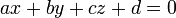, Resolver o seguinte sistema de equações:

.

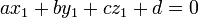
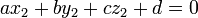
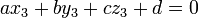Este sistema pode ser resolvido usando Cramer da Regra e manipulações básicas da matriz. Deixar 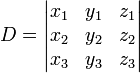. Em seguida,

.

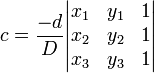Essas equações são paramétricos em d. Definir d igual a qualquer número diferente de zero e substituindo-o para essas equações irá produzir um conjunto de soluções.

• Este plano pode também ser descrito pelo "ponto e de um vector normal" receita atrás referida.

Um vector adequado o normal é dada pela produto cruzado 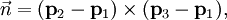e o ponto 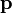pode ser tomada como sendo qualquer um dos pontos dados 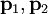ou .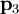

Distância de um ponto a um plano

Para um avião 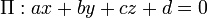e um ponto 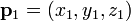não necessariamente deitado no avião, a menor distância 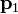para o avião está

Segue que 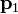se situa no plano Se e só se D = 0.

Se 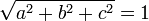o que significa que a, b e c são normalizados, em seguida, a equação torna-se

Linha de intersecção entre dois planos

Planos de interseção dadas descritos por 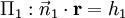e 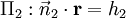, A linha de intersecção é perpendicular a ambos 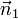e 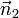e, portanto, paralela ao .

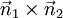Se assumirmos ainda qu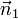e e 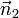são orthonormal então o ponto mais próximo na linha de intersecção com a origem é .

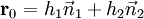Diedro

Dado dois planos de interseção descritos por 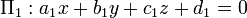e 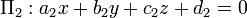, O ângulo diedro entre elas é definido como sendo o ângulo entre as suas direcções normais:

Planes em várias áreas da matemática

Em adição à sua familiarizados geométrico estrutura, com que são isomorfismos isometries no que diz respeito ao produto interno de costume, o avião pode ser visto em vários níveis de outros abstração. Cada nível de abstracção corresponde a um específico categoria.

Em um extremo, tudo geométrica e conceitos métricas podem ser largados para deixar o topológica plano, o que pode ser pensado como um idealizada homotopically folha de borracha trivial infinito, que retém uma noção de proximidade, mas não tem distâncias. O avião topológica tem um conceito de um caminho linear, mas nenhum conceito de uma linha reta. O avião topológico, ou o seu equivalente do disco aberto, é o bairro topológico de base utilizados para a construção superfícies (ou 2-variedades) classificados em topologia low-dimensional. Isomorfismos do plano topológico são todos contínuo bijeções. O avião topológico é o contexto natural para o ramo da teoria dos grafos que lida com grafos planares, e os resultados, tais como o teorema de quatro cores .

O plano pode também ser visto como um espaço afim, cujo isomorfismos são combinações de traduções e mapas lineares não-singulares. A partir deste ponto de vista não há distâncias, mas colinearidade e rácios de distâncias em qualquer linha são preservados.

A geometria diferencial exibe um plano como uma verdadeira 2-dimensional colector , um plano topológica, que é fornecida com um estrutura diferencial. Novamente neste caso, não existe uma noção de distância, mas existe agora um conceito de suavidade de mapas, por exemplo, uma diferenciável ou caminho suave (dependendo do tipo de estrutura diferencial aplicada). Os isomorfismos neste caso são bijeções com o grau escolhido de diferenciabilidade.

Na direcção oposta da abstracção, pode-se aplicar uma estrutura de campo compatível em relação ao plano geométrico, dando origem ao plano complexo e a grande área de análise complexa. O campo complexo tem apenas duas isomorfismos que deixam a verdadeira linha fixa, a identidade e conjugação.

Da mesma forma como no caso real, o avião pode também ser visto como o mais simples, de uma dimensão (ao longo dos números complexos) variedade complexa, às vezes chamado de linha complexo. No entanto, este ponto de vista contrasta com o caso de o plano como um colector verdadeira 2-dimensional. Os isomorfismos são todos bijeções conformados do plano complexo, mas as únicas possibilidades são mapas que correspondem à composição de uma multiplicação por um número complexo e tradução.

Além disso, a geometria euclidiana (que tem zero curvatura em toda a parte) não é a única geometria que o avião possa ter. O plano pode ser um dado geometria esférica usando o projeção estereográfica. Isto pode ser pensado como a colocação de uma esfera no plano (como uma bola no chão), removendo o ponto de início, e que se projecta a esfera para o avião a partir deste ponto). Esta é uma das projecções que podem ser utilizados no fabrico de um mapa plano de uma parte da superfície da Terra. A geometria resultante tem curvatura positiva constante.

Alternativamente, o plano também pode ser dada uma métrica que lhe confere curvatura negativa constante dando o plano hiperbólico. Esta última possibilidade encontra uma aplicação na teoria da relatividade especial no caso simplificado, onde existem duas dimensões espaciais e uma dimensão de tempo. (O plano hiperbólico é um timelike hipersuperfıcie em três dimensões Espaço minkowski).