
Polígono
Informações de fundo
Esta seleção é feita para as escolas de caridade infantil leia mais . Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...

Em geometria um polígono (pron .: / p ɒ l ɪ ɡ ɒ n /) É uma forma plana consistindo em linhas rectas que estão ligados para formar um cadeia fechada ou circuito.
Um polígono é tradicionalmente um avião figura que é delimitada por uma fechado percurso, composta por uma sequência finita de recta segmentos de linha (isto é, por um cadeia poligonal fechada). Estes segmentos são chamados de suas bordas ou lados, e os pontos onde duas bordas encontro são os vértices do polígono (singular: vértice) ou cantos. Um N-gon é um polígono com n lados. O interior do polígono é às vezes chamado de seu corpo. Um exemplo é um polígono 2-dimensional da mais generalizada poli-epítopo em qualquer número de dimensões.
A palavra "polígono" deriva do grego πολύς (polus) "muito", "muitos" e γωνία (Goniá) "canto", "angle", ou γόνυ (Gonu) "joelho".
A noção geométrica de base foi adaptado de várias maneiras para atender propósitos particulares. Os matemáticos são muitas vezes preocupado apenas com a cadeia poligonal fechada e com polígonos simples que não fazer auto-interseção, e podem definir um polígono em conformidade. Geometricamente dois bordos se encontram num canto são necessários para formar um ângulo que não está em frente (180 °); de outro modo, os segmentos de linha será considerado partes de uma única aresta; no entanto matematicamente, tais cantos podem, por vezes, ser permitido. Em domínios relacionados com a computação, o termo polígono assumiu um significado ligeiramente alterado derivado da forma como a forma é armazenada e manipulada em computação gráfica (geração de imagens). Algumas outras generalizações de polígonos são descritos abaixo.
Classificação
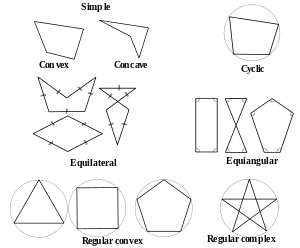
Número de lados
Os polígonos são classificados principalmente pelo número de lados. Veja tabela abaixo .
Convexidade e tipos de não-convexidade
Polígonos podem ser caracterizados pela sua convexidade ou de tipo não-convexidade:
- Convex: qualquer linha traçada através do polígono (e não tangente a uma aresta ou canto) cumpre a sua fronteira exatamente o dobro. Equivalentemente, todos os seus ângulos internos são menos de 180 °.
- Não-convexo: a linha pode ser encontrado que satisfaz seu limite mais do que duas vezes. Em outras palavras, ele contém, pelo menos, um ângulo interior com uma medida superior a 180 °.
- Simples: o limite do polígono não cruzar-se. Todos os polígonos convexos são simples.
- Côncavo: Non-convexo e simples.
- Star-shaped: todo o interior é visível a partir de um único ponto, sem atravessar toda a borda. O polígono tem de ser simples, e pode ser convexa ou côncava.
- Auto-intersecção: o limite do polígono cruza-se. Branko Grünbaum chama esses cóptico, embora este termo não parece ser amplamente utilizado. O complexo termo é usado às vezes em contraste com simples, mas este uso arrisca a confusão com a idéia de um polígono complexo como aquele que existe no complexo Hilbert plano que consiste em dois complexos dimensões.
- Estrela polígono: um polígono que se auto-intersecta de uma forma regular.
Simetria
- Equiangular: todos os seus ângulos de canto são iguais.
- Cíclicos: todos os cantos mentir em um único círculo .
- Isogonal ou vértice-transitivo: todos os cantos se encontram dentro da mesma órbita simetria. O polígono também é cíclico e equiangular.
- Equiláteros: todas as arestas são do mesmo comprimento. (Um polígono com cinco ou mais lados pode ser equilátero sem ser convexa.)
- Isotoxal ou borda-transitivo: todos os lados se encontram dentro da mesma órbita simetria. O polígono também é equilátero.
- Tangencial: todos os lados são tangentes a um círculo inscrito.
- Regular: Um polígono é regular, se é tanto cíclica e equilátero. Um polígono regular não-convexa é chamado um regular polígono estrela.
Propriedades
Geometria euclidiana é assumida por toda parte.
Angles
Qualquer polígono,, auto-intersecção regular ou irregular ou simples, tem como muitos cantos, pois tem os lados. Cada canto tem vários ângulos. Os dois mais importantes são:
- Ângulo Interior - A soma dos ângulos internos de um n-gon é simples (n - 2) π radianos ou (n - 2) 180 graus . Isto é porque qualquer n-gon simples podem ser consideradas como constituídos por (n - 2) triângulos, cada um dos quais tem um valor de ângulo π radianos ou 180 graus. A medida de qualquer ângulo interior de um n-gon regular, é convexa
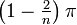 radianos ou
radianos ou 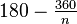 graus. Os ângulos internos de regulares polígonos estrela foram estudados pela primeira vez por Poinsot, no mesmo jornal em que ele descreve a quatro poliedros estrela regular.
graus. Os ângulos internos de regulares polígonos estrela foram estudados pela primeira vez por Poinsot, no mesmo jornal em que ele descreve a quatro poliedros estrela regular.
- Ângulo Exterior - Rastreamento em torno de um n-gon convexo, o ângulo "transformou" em um canto é o ângulo externo ou externo. Rastreando todo o caminho ao redor do polígono faz um completo por sua vez, de modo a soma dos ângulos exteriores deve ser de 360 °. Este argumento pode ser generalizado a côncavos polígonos simples, se ângulos exteriores que giram em sentido contrário são subtraídos a partir do total girado. Traçando em torno de um modo geral n-gon, a soma dos ângulos exteriores (a quantidade total de uma roda nos vértices) pode ser qualquer número inteiro d múltiplo de 360 °, por exemplo 720 ° para uma pentagrama e 0 ° C durante um angular "oito", em que d é a densidade ou Starriness do polígono. Veja também Orbit (dinâmica).
O ângulo exterior é a ângulo complementar ao ângulo interno. Deste a soma dos ângulos internos pode ser facilmente confirmada, mesmo que alguns ângulos internos são mais do que 180 °: indo no sentido horário ao redor, isso significa que um em algum momento vira à esquerda em vez da direita, que é contado como transformar um montante negativo. (Assim, podemos considerar algo como o número de enrolamento da orientação dos lados, em que em cada vértice da contribuição é entre -. 1/2 e 1/2 do enrolamento)
Área e centróide
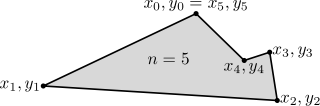
A área de um polígono é a medição da região 2-dimensional fechado por o polígono. Para um não-auto-interseção ( polígono simples) com n vértices, a área e centróide são dadas por:
Para fechar o polígono, os primeiro e último vértices são o mesmo, ou seja, x n, y n = x 0, y 0. Os vértices devem ser ordenados de acordo com a orientação positiva ou negativa (sentido anti-horário ou horário, respectivamente); Se eles estão ordenados de forma negativa, o valor dado pela fórmula área será negativo mas correcta em valor absoluto , mas quando se calcula 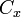 e
e 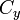 , O valor de assinatura
, O valor de assinatura 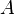 (Que neste caso é negativo) deve ser usado. Isto é comumente chamado de Fórmula de peritos.
(Que neste caso é negativo) deve ser usado. Isto é comumente chamado de Fórmula de peritos.
A fórmula área é derivado, tendo cada aresta AB, e calculando a (assinado) área do triângulo ABO, com um vértice na origem O, tomando o produto cruzado (que dá a área de um paralelogramo) e dividindo por 2. Como um envolve o polígono, esses triângulos com a área de positivo e negativo se sobrepõem, e as áreas entre a origem eo polígono será cancelada fora e somar a 0, enquanto que apenas a área dentro do triângulo de referência permanece. É por isso que a fórmula é chamado Fórmula do Surveyor, uma vez que o "inspector" está na origem; se indo sentido anti-horário, a área positivo é adicionado quando indo da esquerda para a área da direita e negativo é adicionado quando vai da direita para a esquerda, a partir da perspectiva da origem.
A fórmula foi descrito por Meister em 1769 e por Gauss em 1795. Pode-se verificar através da divisão do polígono em triângulos, mas também pode ser visto como um caso especial de O teorema de Green.
A área A de uma polígono simples também pode ser calculado, se os comprimentos dos lados, um 1, A 2, ..., n e um do ângulos exteriores, θ 1, θ 2, ..., n θ são conhecidos. A fórmula é
A fórmula foi descrita em 1963 por Lopshits.
Se o polígono poderá ser desenhado em uma grade igualmente espaçados de tal modo que todos os seus vértices são pontos da grelha, Teorema de Pick dá uma fórmula simples para a área do polígono com base nos números de pontos de grade interior eo limite.
Em cada polígono com p perímetro e área A, o desigualdade isoperimétrica 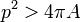 detém.
detém.
Se quaisquer dois polígonos simples de área igual são apresentados, em seguida, o primeiro pode ser cortado em pedaços poligonais que podem ser montados de novo para formar o segundo polígono. Isto é o Bolyai-Gerwien teorema.
A área de um polígono regular, também é dada em termos do raio r do seu círculo inscrito e do seu perímetro por p
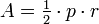 .
.
Este raio é também denominado sua apótema e é muitas vezes representado como um.
A área de um n-gon regular com Inscribed lado s num círculo unitário é
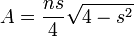 .
.
A área de um n-gon regular em termos do raio r do seu círculo circunscrito e o seu perímetro p é dada por
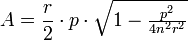 .
.
A área de um n-gon regular, inscrito em um círculo de raio unidade, com o lado interior e s θ ângulo também pode ser expressa como trigonométrica
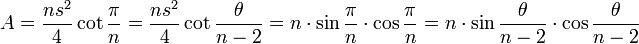 .
.
Os lados de um polígono, em geral, não se determinar a área. No entanto, se o polígono é cíclico dos lados fazer determinar a área. De todos n -gons com dados lados, aquele com a maior área é cíclica. De todos n -gons com um determinado perímetro, aquele com a maior área é regular (e, por conseguinte, cíclico).
Polígonos de auto-interseção
A área de um auto-interceptar polígono pode ser definido de duas formas diferentes, cada uma das quais dá uma resposta diferente:
- Utilizando os métodos acima para polígonos simples, descobrimos que as regiões específicas dentro do polígono pode ter a sua área multiplicado por um factor que chamamos a densidade da região. Por exemplo, o pentágono convexa central no centro de um pentagrama tem densidade 2. As duas regiões triangulares de uma cruz-quadrilátero (como uma figura 8) têm densidades opostas-assinados, e adicionando os seus domínios em conjunto pode dar uma área total de zero para a figura inteira.
- Considerando as regiões fechados como conjuntos de pontos, podemos encontrar a área do conjunto de ponto fechado. Isto corresponde à área do plano coberto pelo polígono, ou para a área de um polígono simples com o mesmo contorno que a auto-interceptar um (ou, no caso de o cruzada quadrilátero, os dois triângulos simples).
Graus de liberdade
Um N-gon tem 2 n graus de liberdade, incluindo 2 para a posição, para uma orientação de rotação, e um para o tamanho global, de modo que n 2 - 4 para moldar. No caso de um linha de simetria este último reduz a n - 2.
Vamos k ≥ 2 Para uma nk Gon com k vezes de simetria rotacional (C k), existem 2 n -. 2 graus de liberdade para a forma. Com simetria espelho de imagem adicional (D k) existem n - 1 graus de liberdade.
Produto das distâncias de um vértice para outros vértices de um polígono regular
Para um N-gon regular inscrito num círculo unitário de raio, o produto das distâncias de um dado vértice para todos os outros vértices é igual a n.
Generalizações de polígonos
Em um sentido amplo, um polígono é uma (sem fins) ou circuito seqüência de segmentos alternados (laterais) e ângulos (cantos) sem limites. Um polígono comum é ilimitado porque a seqüência de volta fecha em si mesmo em um loop ou circuito, enquanto um apeirogon (infinito polígono) é ilimitada, porque continua para sempre. A compreensão matemática moderna é descrever uma sequência estrutural desse tipo em termos de um " polígono abstrato ", que é uma parcialmente ordenado set (CPO) dos elementos. O interior (corpo) do polígono é outro elemento, e (por razões técnicas) por isso é o polytope nulo ou nullitope.
Um polígono geométrica é uma realização do polígono abstratos associados. Isso envolve algum mapeamento de elementos do abstrato para o geométrico. Tal polígono não tem que estar em um avião, ou ter lados retos, ou delimitar uma área, e elementos individuais podem sobrepor-se ou até mesmo coincidem. Por exemplo, uma polígono esférica é desenhado sobre a superfície de uma esfera, e os seus lados são arcos de círculos grandes.
Um Digon é um polígono fechado que tem dois lados e dois cantos. Dois pontos opostos sobre uma superfície esférica, unidos por dois grandes círculos diferente meia produzir um Digon. Tiling a esfera com digons produz um poliedro chamado de hosohedron. Um grande círculo com um ponto de canto adicionado, produz um monogon ou henagon.
Outras realizações desses polígonos são possíveis em outras superfícies, mas no plano euclidiano (flat), seus corpos não podem ser realizados de forma sensata e são considerados degenerada.
A idéia de um polígono tem sido generalizada de várias maneiras. Uma pequena lista de alguns casos degenerados (ou casos especiais) tem a seguinte composição:
- Digon: Interior ângulo de 0 ° no plano euclidiano. Ver observações acima sobre a esfera
- Interior ângulo de 180 °: No plano isso dá uma apeirogon (veja abaixo), na esfera uma diedro
- A polígono de inclinação não está em uma superfície plana, mas ziguezagues em três (ou mais) dimensões. O Polígonos Petrie do poliedros regulares são exemplos clássicos
- A polígono esférico é um circuito de cantos laterais e na superfície de uma esfera
- Um apeirogon é uma sequência infinita de lados e ângulos, a qual não está fechado, mas não tem extremidades porque se estende infinitamente
- A polígono complexo é uma figura semelhante a um polígono comum, que existe no plano Hilbert complexo
Naming polígonos
A palavra "polígono" vem Polygonum latim tardio (um substantivo), do grego πολύγωνον (polygōnon / polugōnon), uso de substantivo neutro de πολύγωνος (polygōnos / polugōnos, o adjetivo masculino), que significa "muitos-angular". Polígonos individuais são nomeados (e, por vezes, classificados) de acordo com o número de lados, a combinação de uma grega -derived prefixo numérico com o sufixo gon, por exemplo, pentágono, dodecagon. O triângulo , quadrilátero ou quadrilátero, e nonagon são exceções. Para grandes números, os matemáticos costumam escrever o numeral em si, por exemplo, 17-gon. Uma variável pode ser usado até mesmo, geralmente n-gon. Isto é útil se o número de lados é usado em uma fórmula .
Alguns polígonos especiais também têm os seus próprios nomes; por exemplo, a regular estrela pentágono é também conhecido como o pentagrama.
| Nome | Edges | Observações |
|---|---|---|
| henagon (ou monogon) | 1 | No plano euclidiano, degenera para uma curva fechada com um único ponto de vértice sobre ele. |
| Digon | 2 | No plano euclidiano, degenera para uma curva fechada com dois pontos de vértice sobre ele. |
| triângulo (ou trigon) | 3 | O polígono mais simples que podem existir no plano euclidiana. |
| quadrilateral (ou quadrado ou tetragon) | 4 | O polígono simples que podem cruzar-se; o polígono mais simples que pode ser côncava. |
| pentágono | 5 | O polígono mais simples que pode existir como uma estrela regular. Uma estrela pentágono é conhecido como um pentagrama ou pentagrama. |
| hexágono | 6 | Evite "sexagon" = Latina [sexo] + grego. |
| heptágono | 7 | Evite "septagon" = Latina [sept-] + grego. O polígono mais simples de tal modo que a forma regular não é construtível com régua e compasso . No entanto, ele pode ser construído usando uma Construção Neusis. |
| octógono | 8 | |
| enneagon ou nonagon | 9 | "Nonagon" é comumente usado, mas se mistura Latina [novem = 9] com o grego. Alguns autores modernos preferem "enneagon", que é puro grego. |
| decágono | 10 | |
| hendecágono | 11 | Evite "undecagon" = Latina [un -] + grego. O polígono mais simples de tal modo que a forma regular não pode ser construído com compasso, régua, e trisector ângulo. |
| dodecágono | 12 | Evite "duodecagon" = Latina [duo -] + grego. |
| tridecagon (ou triskaidecagon) | 13 | |
| tetradecagon (ou tetrakaidecagon) | 14 | |
| pentadecagon (ou quindecagon ou pentakaidecagon) | 15 | |
| hexadecagon (ou hexakaidecagon) | 16 | |
| heptadecagon (ou heptakaidecagon) | 17 | |
| octadecagon (ou octakaidecagon) | 18 | |
| enneadecagon (ou enneakaidecagon ou nonadecagon) | 19 | |
| icosagon | 20 | |
| triacontagon | 30 | |
| hectogon | 100 | "Hectogon" é o nome grego (ver hectómetro), "centagon" é um híbrido latino-grego; nem é amplamente comprovada. |
| polígono de mil lados | 1000 | René Descartes, Immanuel Kant , David Hume , e outros autores utilizaram o polígono de mil lados como um exemplo em discussão filosófica. |
| myriagon | 10.000 | |
| megagon | 1.000.000 | Como com o exemplo Rene Des 'do polígono de mil lados, o polígono milhões lados tem sido utilizada como uma ilustração de um conceito bem definido, que não pode ser visualizada. O megagon também é usado como uma ilustração da convergência de polígonos regulares a um círculo. |
| apeirogon |  | Um polígono degenerada de um número infinito de lados |
Construindo nomes mais elevados
Para construir o nome de um polígono com mais de 20 e menos de 100 bordas, combinar os prefixos como se segue
| Dezenas | e | Ones | sufixo final, | ||
|---|---|---|---|---|---|
| -kai- | 1 | -hena- | Gon | ||
| 20 | icosaedro | 2 | di- | ||
| 30 | triaconta- | 3 | -tri | ||
| 40 | tetraconta- | 4 | -tetra- | ||
| 50 | pentaconta- | 5 | -penta- | ||
| 60 | hexaconta- | 6 | -hexa- | ||
| 70 | heptaconta- | 7 | -hepta- | ||
| 80 | octaconta- | 8 | -octa- | ||
| 90 | enneaconta- | 9 | -ennea- | ||
O "kai" nem sempre é utilizado. As opiniões divergem sobre exatamente quando deveria, ou não precisa, ser utilizado (ver também exemplos acima).
Em alternativa, o sistema utilizado para a nomeação alcanos superiores (hidrocarbonetos completamente saturados) podem ser utilizados:
| Ones | Dezenas | sufixo final, | ||
|---|---|---|---|---|
| 1 | Hen- | 10 | deca- | Gon |
| 2 | Faz- | 20 | -cosa- | |
| 3 | tri- | 30 | triaconta- | |
| 4 | tetra- | 40 | tetraconta- | |
| 5 | penta | 50 | pentaconta- | |
| 6 | hexa- | 60 | hexaconta- | |
| 7 | hepta | 70 | heptaconta- | |
| 8 | octa- | 80 | octaconta- | |
| 9 | ennea- (ou nona-) | 90 | enneaconta- (ou nonaconta-) | |
Isto tem a vantagem de ser compatível com o sistema utilizado para 10- mediante figuras 19 faces.
Isto é, uma figura 42 lados seria chamado como se segue:
| Ones | Dezenas | sufixo final, | nome completo polígono |
|---|---|---|---|
| Faz- | tetraconta- | Gon | dotetracontagon |
e uma figura 50-sided
| Dezenas | e | Ones | sufixo final, | nome completo polígono |
|---|---|---|---|---|
| pentaconta- | Gon | pentacontagon | ||
Mas, além enneagons e decágonos, matemáticos profissionais geralmente preferem a notação numeral acima mencionado (por exemplo, MathWorld tem artigos sobre 17-gons e 257-gons). Exceções existem para a contagem de colaterais que são mais facilmente expressas na forma verbal.
História
Polígonos são conhecidas desde tempos antigos. O polígonos regulares eram conhecidos dos antigos gregos, ea pentagrama, um polígono regular não-convexo ( estrela polígono), aparece no vaso de Aristophonus, Caere, datado do século 7 aC polígonos não-convexos em geral não foram sistematicamente estudadas até o século 14 por Thomas Bradwardine.
Em 1952, Geoffrey Colin Shephard generalizada a ideia de polígonos para o plano complexo, onde cada real dimensão é acompanhado por uma imaginária, para criar polígonos complexos.
Polígonos na natureza
Numerosos polígonos regulares pode ser visto na natureza. No mundo da geologia , cristais têm faces planas, ou facetas, que são polígonos. Quasicristais pode até ter pentágonos regulares como rostos. Outro exemplo fascinante de polígonos regulares ocorre quando o resfriamento de lava faz áreas de hermeticamente embalados hexagonal colunas de basalto , que podem ser vistas na calçada do gigante em Irlanda , ou no Postpile do diabo em Califórnia .

Os hexágonos mais famosas na natureza são encontrados no reino animal. A cera favo de mel feita por abelhas é uma matriz de hexágonos usados para armazenar mel e pólen, e como um lugar seguro para as larvas de crescer. Também existem animais que se tomam a forma aproximada de polígonos regulares, ou, pelo menos, têm a mesma simetria. Por exemplo, estrelas do mar exibir a simetria de um pentágono ou, menos freqüentemente, a heptágono ou outros polígonos. Outro equinodermes, tal como ouriços do mar, às vezes exibir simetrias semelhantes. Embora equinodermos não apresentam exata simetria radial, medusas e Geléias de pente fazer, normalmente quatro vezes ou oito vezes.
Simetria radial (e outra simetria) também é amplamente observado no reino vegetal, particularmente entre flores, e (em menor escala) sementes e frutos, a forma mais comum de tal simetria sendo pentagonal. Um exemplo particularmente impressionante é a carambola, uma fruta ligeiramente picante popular no Sudeste Asiático, cuja secção transversal tem a forma de uma estrela pentagonal.
Afastando-se da terra para o espaço, os primeiros matemáticos que fazem cálculos usando de Newton lei da gravitação descobriu que, se dois corpos (como o sol ea terra) estão orbitando um ao outro, existem certos pontos no espaço, chamado Pontos de Lagrange, onde um corpo menor (como um asteróide ou uma estação espacial) permanecerão em uma órbita estável. O sistema Terra-Sol tem cinco pontos de Lagrange. Os dois mais estável são exatamente 60 graus à frente e atrás da Terra em sua órbita; isto é, que une o centro do Sol e da Terra e um desses pontos de Lagrange estáveis forma um triângulo equilátero. Os astrônomos já encontraram asteróides nestes pontos. Ele ainda está em discussão se é prático para manter uma estação espacial no ponto de Lagrange - embora nunca precisaria de correções de curso, ele teria que frequentemente evitar os asteróides que já estão presentes lá. Já existem satélites e observatórios espaciais nos pontos de Lagrange menos estáveis.
Polígonos em computação gráfica
Um polígono em um sistema de computação gráfica (geração de imagens) é uma forma bidimensional que é modelado e armazenados dentro de seu banco de dados. Um polígono pode ser colorido, sombreado e com textura, e a sua posição na base de dados é definida pelas coordenadas dos seus vértices (cantos).
Convenções de nomes diferem dos matemáticos:
- Um polígono simples não cruzar-se.
- um polígono côncava é um polígono simples tendo pelo menos um ângulo interno maior do que 180 °.
- Um polígono complexo faz cruzar-se.
Uso de polígonos em imagens em tempo real: O sistema de imagem chama-se a estrutura de polígonos necessários para a cena a ser criada a partir do banco de dados. Esta é transferida para a memória activa e, finalmente, para o sistema de exibição (ecrã, monitor de TV, etc.) de modo que a cena pode ser visualizado. Durante este processo, o sistema de imagens torna polígonos em perspectiva correcta pronto para a transmissão dos dados processados para o sistema de exibição. Embora os polígonos são bidimensional, por meio do sistema de computador que são colocadas numa cena visual na orientação tridimensional correcta, de modo que como o ponto de observação se move através da cena, que é percebido em 3D.
Morphing: Para evitar efeitos artificiais nas fronteiras do polígono onde os aviões de polígonos contíguos estão no ângulo diferente, os chamados "MorphingAlgorithms" são usados. Estes mistura, suavizar ou suavizar as bordas de polígonos de modo que a cena parece menos artificial e mais parecido com o mundo real.
Polígonos malha: O número de polígonos em malha ("malha" é como uma rede de pesca) pode ser até duas vezes maior que de polígonos unmeshed free-standing, particularmente se os polígonos são contíguos. Se uma malha quadrada tem n + 1 pontos (vértices) de cada lado, existem n quadrados quadrado na malha, ou 2 n ao quadrado triângulos desde há dois triângulos em um quadrado. Há (n + 1) 2/2 (N2) por vértices do triângulo. Onde n é grande, isso se aproxima de um meio. Ou, cada vértice dentro da malha quadrada conecta quatro bordas (linhas).
Contagem de polígonos: Uma vez que um polígono pode ter muitos lados e precisa de muitos pontos de defini-lo, a fim de comparar um sistema de imagem com outro ", contagem de polígonos" é geralmente considerado como um triângulo. Ao analisar as características de um sistema de imagem particular, a definição exata de contagem de polígonos deve ser obtida, uma vez que se aplica a esse sistema, pois existe uma certa flexibilidade no processamento que faz com que comparações para se tornar não-trivial.
Contagem Vertex: Embora o uso dessa métrica parece estar mais próximo da realidade que ainda deve ser tomado com um pouco de sal. Uma vez que cada vértice pode ser aumentado com outros atributos (tal como a cor ou normal) a quantidade de processamento envolvido não pode ser trivialmente inferida. Além disso, o vértice aplicado transformar deve ser contabilizada, assim informações de topologia específico para o sistema que está sendo avaliada como transformar pós-cache pode apresentar variações consistentes nos resultados esperados.
Ponto de teste polígono: Em computação gráfica e geometria computacional, muitas vezes é necessário para determinar se um dado ponto P = (x 0, y 0) encontra-se dentro de um polígono simples dada por uma sequência de segmentos de linha. É conhecido como o Ponto de teste polígono.

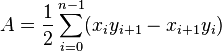
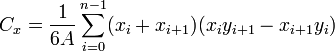
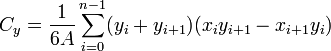
![\ Begin {align} A = \ frac12 (a_1 [a_2 \ sin (\ theta_1) + a_3 \ sin (\ theta_1 + \ theta_2) + \ cdots + a_ {n-1} \ sin (\ theta_1 + \ theta_2 + \ cdots + \ theta_ {n-2})] \\ {} + a_2 [a_3 \ sin (\ theta_2) + a_4 \ sin (\ theta_2 + \ theta_3) + \ cdots + a_ {n-1} \ sin (\ theta_2 + \ cdots + \ theta_ {n-2})] \\ {} + \ cdots + a_ {n-2} [a_ {n-1} \ sin (\ theta_ {n-2})]) \ end {align}](../../images/2168/216877.png)

