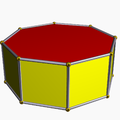
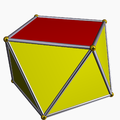
Poliedro
Você sabia ...
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
|
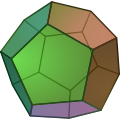
Um poliedro (poliedros plural ou poliedros) é muitas vezes definido como um geométrico objeto com faces planas e bordas retas (a palavra vem do poliedro Grego clássico πολυεδρον, a partir de poli-, haste de πολυς, "muitos", + -edron, forma de εδρον, "base", "cadeira", ou "face").
Esta definição de um poliedro não é muito preciso, e para um matemático moderna é bastante insatisfatório. Grünbaum (1994, p.43) observaram que:
O Pecado Original na teoria de poliedros remonta a Euclides , e através de Kepler , Poinsot, Cauchy e muitos outros ... [em que] em cada etapa ... os escritores não conseguiu definir o que são os "poliedros" ...
Matemáticos modernos nem mesmo concordam sobre exatamente o que faz algo um poliedro.
O que é um poliedro?
Podemos dizer que, pelo menos, um poliedro é construído a partir de diferentes tipos de elemento ou entidade, cada um associado com um número diferente de dimensões:
- 3 dimensões: O corpo é delimitada por as faces, e é geralmente o volume no seu interior.
- 2 dimensões: a cara limitada por um circuito de arestas, e é geralmente um (plano) região plana chamado um polígono . Os rostos juntos compõem a superfície poliédrica.
- 1 dimensão: An junta-se a uma aresta de vértice para outro e uma face a outra, e é normalmente uma linha de algum tipo. As bordas juntos formam o esqueleto poliédrico.
- 0 dimensões: a vértice (vértices plural) é um canto ponto.
- Dimensão -1: A nulidade é uma espécie de não-entidade exigido por abstratas teorias.
De modo mais geral em matemática e outras disciplinas ", poliedro" é usado para se referir a uma variedade de construções relacionadas, alguns geométrica e outros puramente algébrica ou abstrato.
Uma característica definidora de quase todos os tipos de poliedros é que apenas dois rostos se juntar ao longo de qualquer aresta comum. Isso garante que a superfície poliédrica está continuamente ligado e não termina abruptamente ou dividir em direções diferentes.
A poliedros é um exemplo 3-dimensional do mais geral poli-epítopo em qualquer número de dimensões.
Características
Naming poliedros
Poliedros são geralmente nomeados de acordo com o número de faces. O sistema de nomeação é novamente baseado em grego clássico, por exemplo tetraedro (4), pentaedro (5), hexaedro (6), heptahedron (7), triacontahedron (30), e assim por diante.
Muitas vezes isso é qualificado por uma descrição dos tipos de rostos presentes, por exemplo, o Dodecaedro rômbico contra o Dodecaedro pentagonal.
Outros nomes comuns que indicam alguma operação foi realizada num poliedro mais simples, por exemplo, a cubo truncado parece um cubo com seus cantos cortados, e tem 14 faces (por isso também é um exemplo de uma tetrakaidecahedron).
Alguns poliedros especial têm crescido seus próprios nomes ao longo dos anos, como O monstro de Miller ou o Szilassi poliedro.
Edges
Bordas tem duas características importantes (a menos que o poliedro é complexa ):
- Uma aresta junta-se apenas dois vértices.
- Uma aresta junta-se a apenas dois rostos.
Estas duas características são dupla uns aos outros.
Euler característica
A característica de Euler χ relaciona o número de vértices V, bordas E, F e enfrenta de um poliedro:
- χ = V - E + F.
Para simplesmente poliedro conexo, χ = 2. Para uma discussão detalhada, veja Provas e Refutações por Imre Lakatos.
Dualidade

Para cada poliedro existe uma poliedro dual ter rostos no lugar de vértices da originais e vice-versa. Na maioria dos casos, a dupla pode ser obtido pelo processo de reciprocidade esférica.
Figura Vertex
Para cada vértice pode-se definir um número de vértice que consiste nos vértices se juntou a ele. O vértice é dito para ser regular se isto é um polígono regular e simétrica em relação a toda a poliedro.
Poliedros tradicional
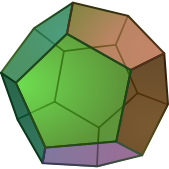
Na geometria , um poliedro é tradicionalmente uma forma tridimensional que é constituído por um número finito de poligonal rostos que são partes de aviões ; os rostos se reunir em pares ao longo bordas que estão em linha reta segmentos, e as bordas se encontram em pontos chamados vértices. Cubes , e prismas pirâmides são exemplos de poliedros. O poliedro envolve um volume limitado no espaço tridimensional; às vezes este volume interior é considerada como fazendo parte do poliedro, por vezes, apenas a superfície é considerada, e, ocasionalmente, apenas o esqueleto de arestas.
Um poliedro é dito ser Convex se a sua superfície (compreendendo as suas faces, arestas e vértices) não se cruzam em si e do segmento linha que une dois pontos quaisquer do poliedro está contido no interior e na superfície.
Poliedros simétricos
Muitos dos poliedros mais estudados são altamente simétrico .
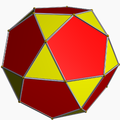
Claro que é fácil distorcer tais poliedros para que eles não são simétricas. Mas onde um nome poliédrico é dada, tal como icosidodecaedro, a geometria mais simétrica é quase sempre implícita, salvo indicação em contrário.
Alguns dos nomes mais comuns, em particular, são muitas vezes utilizados com "regular" na frente ou implícita, porque para cada existem diferentes tipos que têm pouco em comum, exceto por ter o mesmo número de rostos. Estes são o tetraedro , cubo , octaedro , dodecaedro e icosaedro:
Poliedros das maiores simetrias têm todos de algum tipo de elemento - as faces, arestas e / ou vértices, dentro de uma única órbita simetria. Existem várias classes de tais poliedros:
- Isogonal ou Vertex-transitivo se todos os vértices são o mesmo, no sentido de que para quaisquer dois vértices existe uma simetria do poliedro mapear o primeiro isometricamente para o segundo.
- Isotoxal ou -Edge transitória se todas as arestas são o mesmo, no sentido de que para quaisquer duas extremidades existe uma simetria do mapeamento poliedro isometricamente o primeiro para o segundo.
- Isohedral ou Cara-transitivo se todas as faces são o mesmo, no sentido de que para quaisquer duas faces existe uma simetria do mapeamento poliedro isometricamente o primeiro para o segundo.
- Regular se for vértice-transitivo, edge-transitiva e transitivo-face (isso implica que cada rosto é o mesmo polígono regular; isso também implica que cada vértice é regular).
- Quasi-regular, se é vértice-transitivo e edge-transitivo (e, portanto, tem rostos regulares), mas não enfrentam-transitiva. A dupla quasi-regular é transitivo-face e borda-transitivo (e, portanto, cada vértice é regular) mas não vértice-transitivo.
- Semi-regular se for vértice-transitivo, mas não borda-transitivo, e cada rosto é um polígono regular. (Esta é uma das várias definições do termo, dependendo do autor. Algumas definições se sobrepõem com a classe quasi-regular). A dupla semi-regular-face é transitivo, mas não vértice-transitivo, e cada vértice é regular.
- Uniforme se for vértice-transitivo e cada rosto é um polígono regular, ie é regular, quasi-regular ou semi-regular. A dupla-face uniforme é transitivo e tem vértices regulares, mas não é necessariamente vértice-transitivo).
- Noble se é transitivo-face e vértice-transitivo (mas não necessariamente borda-transitivo). Os poliedros regulares também são nobres; eles são a única poliedros uniformes nobre.
Um poliedro podem pertencer ao mesmo grupo de simetria global como uma das mais elevada simetria, mas terá vários grupos de elementos (por exemplo caras) em diferentes órbitas de simetria.
Poliedros uniformes e seus duais
Poliedros uniformes são vértice-transitivo e cada rosto é uma polígono regular. Eles podem ser regular, quasi-regular, ou semi-regular, e pode ser convexo ou estrelado.
O uniforme duais são face-transitivo e cada número de vértice é um polígono regular.
Face-transitividade de um poliedro corresponde ao vértice-transitividade da dupla e, inversamente, e edge-transitividade de um poliedro corresponde à beira-transitividade da dupla. Na maioria dos duos de poliedros uniformes, os rostos são polígonos irregulares. A poliedros regulares são uma excepção, uma vez que eles são dupla uns aos outros.
Cada poliedro uniforme compartilha a mesma simetria como sua dupla, com as simetrias de rostos e vértices simplesmente trocados. Devido a isso, algumas autoridades consideram os duais como uniforme também. Mas esta idéia não é mantido amplamente: um poliedro e suas simetrias não são a mesma coisa.
O poliedro uniforme e seus duais são tradicionalmente classificadas de acordo com seu grau de simetria, e se eles são convexa ou não.
| Uniforme convexo | Uniforme convexa dupla | Uniforme Estrela | Estrela uniforme dupla | |
|---|---|---|---|---|
| Regular | Sólidos platônicos | Kepler-Poinsot poliedros | ||
| Quasiregular | Sólidos de Arquimedes | Sólidos Catalão | (Sem nome especial) | (Sem nome especial) |
| Semiregular | (Sem nome especial) | (Sem nome especial) | ||
| Prismas | Dipyramids | Estrela Prismas | Estrela Dipyramids | |
| Antiprisms | Trapezohedra | Estrela Antiprisms | Estrela Trapezohedra | |
Poliedros Noble
A nobre poliedro é tanto isohedral (equal-faced) e isogonal (igual pontas). Além da poliedros regulares, existem muitos outros exemplos.
O dual de um poliedro nobre também é nobre.
Grupos de simetria
A poliédrica grupos de simetria são todos grupos de pontos e incluem:
- T - quiral simetria tetraédrica; o grupo de rotação para um regular tetraedro ; fim 12.
- T d - completa simetria tetraédrica; o grupo de simetria para um regular tetraedro ; fim 24.
- T h - simetria pyritohedral; 24. A fim de simetria de um pyritohedron.
- O - quiral simetria octaédrica, o grupo de rotação do cubo e octaedro ; fim 24.
- O h - completa simetria octaédrica; o grupo de simetria do cubo e octaedro ; fim 48.
- I - quiral simetria icosaédrica; o grupo da rotação icosaedro eo dodecaedro; fim 60.
- I h - completos simetria icosaédrica; o grupo de simetria do icosaedro eo dodecaedro; encomendar 120.
- Nv C - n vezes de simetria piramidal
- D nh - n vezes de simetria prismático
- D nv - n vezes de simetria antiprismatic
Aqueles com simetria quiral não tem simetria de reflexão e, portanto, têm dois enantiomorphous formas que são reflexos um do outro. Os arrebitado poliedros de Arquimedes têm essa propriedade.
Outros poliedros regulares com rostos
Rostos regulares iguais
Algumas famílias de poliedros, onde cada rosto é o mesmo tipo de polígono:
- Deltahedra tem de triângulo equilátero para rostos.
- No que respeita à poliedros cujas faces são todos os quadrados: se faces coplanares não são permitidos, mesmo se eles estão desligados, não é apenas o cubo. Caso contrário, existe também é o resultado de colar seis cubos para os lados de um, todos os sete do mesmo tamanho; ele tem 30 faces quadradas (contando rostos desconectadas no mesmo plano como separado). Isso pode ser estendido em um, dois ou três direções: podemos considerar a união de arbitrariamente muitas cópias destas estruturas, obtidos por traduções do (expresso em tamanhos cubo) (2,0,0), (0,2,0 ), e / ou (0,0,2), portanto, com cada par adjacente ter um cubo comum. O resultado pode ser qualquer conjunto de cubos conectado com posições (a, b, c), com números inteiros a, b, c, dos quais um, no máximo, é mesmo.
- Não há nenhum nome especial para poliedros cujas faces estão todos pentágonos equilátero ou pentagramas. Há infinitamente muitos deles, mas apenas um é convexa: o dodecaedro. O resto são montados por (colar) combinações dos poliedros regulares descrito anteriormente: o dodecaedro, o pequeno dodecaedro estrelado, o grande dodecaedro estrelado eo grande icosaedro.
Não existe nenhum poliedro cujos rostos são todos idênticos e são polígonos regulares com seis ou mais lados, porque o vértice de três hexágonos regulares define um plano. (Ver poliedro inclinação infinita para exceções com zig-zague figuras de vértice.)
Deltahedra
A deltaedro (deltahedra plural) é um poliedro cujos rostos são todos de triângulo equilátero. Há infinitamente muitos deltahedra, mas apenas oito deles são convexas:
- 3 poliedros convexos regulares (3 dos sólidos platônicos)
- 5 não uniforme poliedros convexos (5 dos sólidos Johnson)
- Dipyramid Triangular
- Dipyramid Pentagonal
- Desprezo disphenoid
- Prisma triangular Triaugmented
- Dipyramid quadrado Gyroelongated
Sólidos Johnson
Norman Johnson procurado poliedros que não uniforme tinham rostos regulares. Em 1966 , ele publicou uma lista de 92 sólidos convexos, agora conhecido como o Sólidos Johnson, e deu-lhes os seus nomes e números. Ele não conseguiu provar que havia apenas 92, mas ele fez conjectura que não houve outros. Victor Zalgaller em 1969 provou que a lista de Johnson estava completa.
Outros importantes famílias de poliedros
Pirâmides
Pyramids incluem alguns dos mais famosos de todos e poliedros consagrada pelo tempo.
Constelações e facettings
 |  |  |
 | | |  |
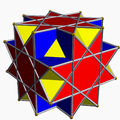
Stellation de um poliedro é o processo de alargar as faces (dentro de seus aviões) para que eles se encontram para formar um novo poliedro.
É o inverso exacta para o processo de talhar que é o processo de remoção de partes de um poliedro, sem criar quaisquer novos vértices.
Zonohedra
A zonohedron é uma poliedros convexos, onde cada rosto é um polígono com inversão simetria ou, de forma equivalente, simetria sob rotações de 180 °.
Compostos
Poliédrica compostos são formados como compostos de duas ou mais poliedros.
Estes compostos, muitas vezes compartilham os mesmos vértices como outros poliedros e muitas vezes são formados por stellation. Alguns estão listados na lista de modelos de poliedro Wenninger.
Orthogonal Polyhedra
Um poliedro ortogonal é um tudo de cujas faces se encontram em ângulo recto, e cuja totalidade das bordas são paralelas aos eixos de um sistema de coordenadas cartesiano. Além de uma caixa retangular, poliedros ortogonais são não-convexa. Eles são os análogos de 2D 3D polígonos ortogonais (também conhecidos como polígonos retilíneos). Poliedros ortogonais são utilizadas em geometria computacional, em que a sua estrutura restrita permitiu avanços na problemas não resolvidos em poliedros arbitrária, por exemplo, desdobramento a superfície de um poliedro de um net (poliedro).
Generalizações de poliedros
O nome "poliedro 'passou a ser utilizado para uma variedade de objectos com propriedades estruturais semelhantes a poliedros tradicional.
Apeirohedra
Uma superfície poliédrica clássico compreende finito, regiões planas delimitadas, juntou-se em pares ao longo das bordas. Se essa superfície se estende indefinidamente ele é chamado de apeirohedron. Os exemplos incluem:
- Pavimentações ou pavimentações do plano.
- Estruturas de esponja-como chamadas poliedros inclinação infinito.
Veja também: Apeirogon - infinito polígono regular: {∞}
Complexo poliedros
A poliedro é um complexo que é construído em unitária 3-espaço. Este espaço tem seis dimensões: três reais correspondentes ao espaço comum, com cada um acompanhado por uma dimensão imaginária. Ver, por exemplo Coxeter (1974).
Poliedros Curved
Algumas áreas de estudo permitem poliedros ter faces curvas e bordas.
Poliedros esférica
A superfície de uma esfera pode ser dividido por segmentos de linha em regiões limitadas, para formar um poliedro esférica. Grande parte da teoria de poliedros simétrico é mais convenientemente obtido desta forma.
Poliedros esféricas têm uma história longa e respeitável:
- Os primeiros conhecidos poliedros artificiais são poliedros esférico esculpida em pedra.
- Poinsot usado poliedros esférico para descobrir a quatro poliedros regulares estrela.
- Coxeter usou para enumerar todos, mas um dos poliedros uniforme.
Alguns poliedros, como hosohedra, existem apenas como poliedros esférica e não têm análogo flat-faced.
Curved poliedros spacefilling
Dois tipos importantes são os seguintes:
- Bolhas na froths e espumas.
- Spacefilling formulários utilizados na arquitetura. Ver, por exemplo, Pearce (1978).
Mais precisa ser dito sobre estes, também.
Poliedros Geral
Mais recentemente matemática definiu um poliedro como um conjunto em reais afim (ou euclidiana ) de qualquer espaço n-dimensional de que tem lados planos. Pode ser definido como a união de um número finito de poliedros convexos, onde um poliedro convexo é qualquer conjunto que é a interseção de um número finito de meias espaços. Ele pode ser delimitado ou ilimitado. Neste sentido, uma poli-epítopo é um poliedro limitada.
Todos os poliedros tradicionais são poliedros geral, e além disso, existem exemplos como:
- Um quadrante no plano. Por exemplo, a região do plano cartesiano que consiste em todos os pontos acima do eixo horizontal e para a direita do eixo vertical: {(x, y): x ≥ 0, y ≥ 0}. Os seus lados são os dois eixos positivos.
- Um octante no espaço euclidiano de 3, {(x, y, z): ≥ x 0, y ≥ 0, z ≥ 0}.
- Um prisma de extensão infinita. Por exemplo, um prisma quadrado duplamente infinito no espaço de 3, consistindo de um quadrado no -plane xy varrido ao longo do -axis z: {(x, y, z): 0 ≤ ≤ x 1, y 0 ≤ ≤ 1} .
- Cada célula numa Tessellation Voronoi é um poliedro convexo. Na disposição de Voronoi de um conjunto S, a célula de uma correspondente a um ponto c ∈ S é limitada (por conseguinte, um poliedro tradicional) quando c situa-se no interior da fecho convexo de S, e de outra forma (quando c encontra-se no limite do fecho convexo de S) Um é ilimitado.
Oco poliedros faced ou esquelético
Não é necessário preencher o rosto de uma figura antes que possamos chamá-lo de um poliedro. Por exemplo Leonardo da Vinci concebeu modelos de quadros dos sólidos regulares, que ele desenhou para O livro de Pacioli Divina Proportione. Nos tempos modernos, Branko Grünbaum (1994) fez um estudo especial desta classe de poliedros, no qual desenvolveu uma idéia inicial de poliedros abstrato. Ele definiu um rosto como um conjunto ordenado de vértices ciclicamente, e permitiu rostos para ser deforme, bem como planar.
Pavimentações ou tilings
Pavimentações ou pavimentações do plano são por vezes tratados como poliedros, porque eles têm muito em comum. Por exemplo os regulares pode ser dada Schläfli símbolos.
Poliedros não-geométrica
Várias construções matemáticas foram encontrados para ter propriedades também apresentam em poliedros tradicional.
Poliedros topológica
A polytope topológico é um espaço topológico dada juntamente com uma decomposição específica em formas que são topologicamente equivalente a polytopes convexas e que estão ligados uns aos outros de maneira regular.
Tal figura é chamado simplicial se cada uma das suas regiões é uma simplex, ou seja, em um espaço n-dimensional de cada região tem um n vértices. O dual de um politopo simplicial é chamado simples. Da mesma forma, uma classe amplamente estudada de polytopes (poliedros) é a de poliedros cúbico, quando o bloco de construção básico é um cubo de n-dimensional.
Abstract poliedros
Um poliedro é um resumo parcialmente ordenado set (CPO) dos elementos. Teorias diferem em detalhe, mas, essencialmente, os elementos do conjunto correspondem ao corpo, faces, arestas e vértices do poliedro. O conjunto vazio corresponde ao policação nulo, ou nullitope, que tem uma extensibilidade de -1. Estes posets pertencem à família maior de polytopes abstratas em qualquer número de dimensões.
Poliedros como gráficos
Qualquer poliedro dá origem a um gráfico, ou esqueleto, com vértices e arestas correspondentes. Assim terminologia gráfico e as propriedades podem ser aplicadas a poliedros. Por exemplo:
- Devido a Steinitz teorema poliedros convexos estão em correspondência um-para-um com gráficos 3-planares conectadas.
- O tetraedro dá origem a um grafo completo (K 4). É o único poliedro a fazê-lo.
- O octaedro dá origem a um fortemente gráfico regular, porque vértices adjacentes sempre tem dois vizinhos comuns, e os vértices não adjacentes têm quatro.
- O Sólidos de Arquimedes dar origem a gráficos regulares: 7 dos sólidos de Arquimedes são de grau 3, 4 do grau 4, e os restantes 2 são pares quirais de grau 5.
História
Pré-história
Pedras esculpidas em formas que mostram as simetrias de vários poliedros foram encontrados na Escócia e pode ser tanto um 4000 anos de idade. Estas pedras mostram não só a forma de vários polyehdra simétrica, mas também as relações entre a dualidade de alguns deles (ou seja, que os centros das faces do cubo dá os vértices de um octaedro, e assim por diante). Exemplos destas pedras estão em exposição no Sala de John Evans, do Ashmolean Museum em Oxford University . É impossível saber por que esses objetos foram feitas, ou como o escultor ganhou a inspiração para eles.
Outros poliedros têm naturalmente a sua marca na arquitetura - cubos e cuboids ser exemplos óbvios, com as primeiras pirâmides de quatro lados do antigo Egito também que datam da Idade da Pedra.
O Etruscos precedida gregos na sua sensibilização de, pelo menos, alguns dos poliedros regulares, como evidenciado pela descoberta perto Pádua (no norte da Itália ), no final de 1800 de um dodecaedro feito de pedra-sabão, e que datam mais de 2.500 anos (Lindemann, 1987). Pyritohedric cristais são encontrados no norte da Itália.
Gregos
Os primeiros registros escritos conhecidos de essas formas vêm de clássicos gregos autores, que também deu a primeira descrição matemática conhecido deles. Os gregos antigos estavam interessados principalmente no poliedros regulares convexa, enquanto Archimedes mais tarde expandiu seu estudo para o convexo poliedros uniforme.
Muçulmanos e chineses
Após o fim da era clássica, os estudiosos islâmicos continuou a fazer avanços, por exemplo, no século X Abu'l Wafa descritos os poliedros regulares e quasiregular esférica convexa. Enquanto isso, na China, a dissecção do cubo para a sua característica tetraedro (orthoscheme) e sólidos relacionados foi usado como a base para calcular os volumes de terra a ser movido durante escavações de engenharia.
Renascença
Muito a ser dito aqui: Piero della Francesca, Pacioli, Leonardo Da Vinci, Wenzel Jamnitzer, Durer, etc. levando até Kepler.
Poliedros Estrela
Por quase 2000 anos, o conceito de um poliedro tivesse permanecido tão desenvolvido pelos antigos matemáticos gregos.
Johannes Kepler percebeu que polígonos estrela poderia ser usado para construir poliedros estrela, que têm polígonos regulares não convexos, tipicamente pentagramas como rostos. Alguns destes poliedros estrela pode ter sido descoberto antes da época de Kepler, mas ele foi o primeiro a reconhecer que eles poderiam ser considerados "regular" se alguém removeu a restrição de que politopos regulares ser convexo. Mais tarde, Louis Poinsot percebeu que estrela figuras vértice (circuitos em torno de cada canto) também pode ser usado, e os restantes dois descoberto poliedros regulares estrela. Cauchy provou lista de Poinsot completa, e Cayley deu-lhes os seus nomes ingleses aceitos: (Kepler) a pequeno dodecaedro estrelado e grande dodecaedro estrelado, e (Poinsot de) o grande icosaedro e grande dodecaedro. Coletivamente, eles são chamados a Kepler-Poinsot poliedros.
Os poliedros Kepler-Poinsot podem ser construídos a partir dos sólidos Platônicas por um processo chamado stellation. A maioria das constelações não são regulares. O estudo das constelações dos sólidos platônicos foi dado um grande impulso por HSM Coxeter e outros em 1938, com o agora famoso papel A 59 icosahedra. Este trabalho foi recentemente re-publicado (Coxeter, 1999).
O processo recíproco para stellation é chamada talhar (ou lapidação). Cada stellation de um politopo é dupla, ou recíproco, para alguns talhar da dupla poli-epítopo. A poliedros regulares estrela também pode ser obtido por talhar os sólidos platônicos. Ponte 1974 enumerou as facettings mais simples do dodecaedro, e retribuiu-os a descobrir uma stellation do icosaedro que estava faltando do famoso "59". Mais foram descobertos desde, ea história ainda não terminou.
Veja também:
- Poliedro regular: História
- Politopo regular: História da descoberta.
Poliedros na natureza
Para ocorrências naturais de poliedros regulares, consulte Poliedro regular: História.
Poliedros irregulares aparecem na natureza como cristais .
Livros sobre poliedros
Livros introdutórios, também adequado para uso escolar
- Cromwell, P .; Polyhedra, CUP hbk (1997), pbk. (1999).
- Cundy, HM & Rollett, AP; Modelos matemáticos, primeiro Edn. hbk OUP (1951), segundo Edn. hbk OUP (1961), terceiro Edn. pbk Tarquin (1981).
- Holden; Formas, espaço e simetria, (1971), Dover pbk (1991).
- Pearce, P e Pearce, S: Polyhedra primer, Van Nost. Reinhold (maio de 1979), ISBN-10: 0442264968 ISBN-13: 978-0442264963.
- Tarquin publicações: livros de cut-out e fazer modelos de cartões.
- Wenninger, modelos M .; poliedro para a sala de aula, pbk (1974)
- Wenninger, modelos M .; poliedro, CUP hbk (1971), pbk (1974).
- Wenninger, M .; Spherical modelos, CUP.
- Wenninger, M .; dupla modelos, CUP.
Nível de graduação
- Coxeter, HSM DuVal, Flather & Petrie; O cinqüenta e nove icosahedra, 3 Edn. Tarquin.
- Coxeter, HSM Doze ensaios geométricos. Republicado como a beleza da geometria, Dover.
- Crescimento Thompson, Sir D'AW On e forma, (1943). (Não sei se esta é a categoria certa para este, eu não li).
Design e arquitetura viés
- Critchlow, K .; Ordem no espaço.
- Pearce, P .; Estrutura na natureza é uma estratégia para o projeto, MIT (1978)
- Williams, R .; A base geométrica da estrutura natural, Dover (1979).
Textos matemáticos avançados
- Coxeter, HSM; regular Polytopes 3 Edn. Dover (1973).
- Coxeter, HSM; polytopes complexos regulares, CUP (1974).
- Lakatos, Imre; Provas e Refutações, Cambridge University Press (1976) - discussão da prova de Euler característica
- Vários mais a acrescentar aqui.
Livros históricos
- Brückner, Vielecke und Vielflache (polígonos e poliedros), (1900).
- Fejes Toth, L .;