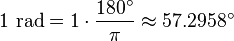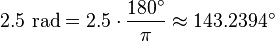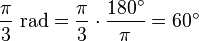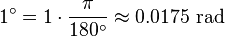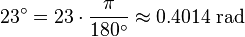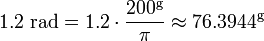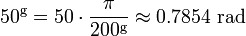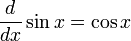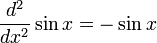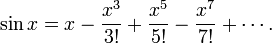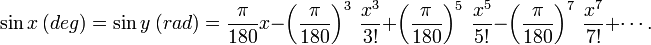Radiano

Alguns ângulos comuns, medido em radianos. Todos os polígonos são polígonos regulares.

O radiano é uma unidade de avião ângulo , igual a 180 / π graus , ou cerca de 57,2958 graus. É a unidade padrão de medição angular em todas as áreas de matemática além do nível elementar.

O radiano é representada pelo símbolo "rad" ou, mais raramente, pela c sobrescrito (por "medida circular"). Por exemplo, um ângulo de 1.2 radianos seria escrito como "1,2 rad" ou "1.2 ^c" (o segundo símbolo pode ser confundido com um grau: "1.2 °"). No entanto, o radiano é matematicamente considerado um "número puro" que não precisa de símbolo da unidade e na escrita matemática o símbolo "rad" é quase sempre omitido. Na ausência de qualquer símbolo radianos são assumidos, e quando são destinados a graus símbolo É usado.

O radiano é um antigo Unidade suplementar SI, mas esta categoria foi abolida em 1995 eo radiano é agora considerado um SI unidade derivada. A unidade SI de medição do ângulo sólido é a esterradiano.

Definição

Um ângulo de 1 radiano subtende um arco de comprimento igual ao raio do círculo .

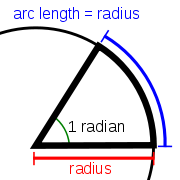
Um radiano é o ângulo subtendido no centro de um círculo por um arco de circunferência que é igual ao comprimento da raio do círculo.

De modo mais geral, a magnitude em radianos, de qualquer ângulo subtendido por dois raios é igual à razão entre o comprimento do arco fechado para o raio do círculo; isto é, = θ s / r, onde θ é o ângulo subtendido em radianos, S é o comprimento do arco, e r é o raio. Por outro lado, o comprimento do arco fechado é igual ao raio multiplicado pela grandeza do ângulo em radianos; isto é, s = rθ.

Segue-se que a magnitude em radianos de uma volta completa (360 °) é o comprimento de toda a circunferência dividido pelo raio, ou 2π r / r, ou 2π. Assim 2π radianos é igual a 360 graus, o que significa que um radiano é igual a 180 / π graus.

História

O conceito de medida radiano, em oposição ao grau de um ângulo, deveria ser creditado Roger Cotes em 1714. Ele teve o radiano em tudo, menos no nome, e ele reconheceu sua naturalidade como uma unidade de medida angular.

O termo radian apareceu pela primeira vez na imprensa em 5 de junho de 1873 , em questões do exame definido pela James Thomson (irmão de Lord Kelvin ) em Colégio Rainha, Belfast . Ele usou o termo tão cedo quanto 1871, enquanto em 1869, Thomas Muir, em seguida, da Universidade de St Andrews , vacilava entre rad, radial e radiano. Em 1874 , Muir adotado radian depois de uma consulta com James Thomson.

Conversões

Conversão entre radianos e graus

Tal como referido acima, um radiano é igual a 180 / π graus. Assim, para converter de radianos em graus, multiplique por 180 / π. Por exemplo,

Por outro lado, para converter de graus em radianos, multiplique por π / 180. Por exemplo,

Você também pode converter radianos em revoluções dividindo-se o número de radianos por 2π.

A tabela mostra a conversão de alguns ângulos comuns.

Degrees	0 °	30 °	45 °	60 °	90 °	180 °	270 °	360 °
Radians	0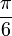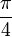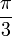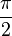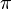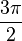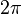

Conversão entre radianos e grados

2π radianos é igual a uma volta completa, o que é de 400 ^g. Então, para converter de radianos em graduados multiplicar por 200 / π, e converter de graduados em radianos, multiplique por π / 200. Por exemplo,

Razões pelas quais radianos são preferidos em matemática

No cálculo ea maioria dos outros ramos da matemática além geometria prática, os ângulos são universalmente medido em radianos. Isto é porque radianos tem um "naturalidade" matemática que leva a uma formulação mais elegante de um número de resultados importantes.

Mais notavelmente, os resultados em análise envolvendo funções trigonométricas são simples e elegante quando os argumentos das funções são expressos em radianos. Por exemplo, a utilização de radianos leva à simples limite de fórmula

,

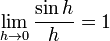que é a base de muitas outras identidades em matemática, incluindo

Devido a estas e outras propriedades, as funções trigonométricas aparecer em soluções para os problemas matemáticos que não são, obviamente, relacionados com significados geométricas das funções (por exemplo, as soluções para a equação diferencial d ² y / dx ² = - y, a avaliação de a integral ∫ dx / (1 + x ^2), e assim por diante). Em todos os casos verificou-se que os argumentos para as funções são naturalmente mais escrito na forma que corresponde, em contextos geométricas, para a medição dos ângulos radianos.

As funções trigonométricas também têm expansões em séries simples e elegante quando radianos são usados; por exemplo, a seguinte série de Taylor para sen x:

Se x foram expressos em graus, em seguida, a série iria conter factores desorganizados envolvendo poderes de π / 180: se x é o número de graus, o número de radianos é y = x π / 180, assim

Matematicamente importantes relações entre o seno e co-seno e funções da função exponencial (ver, por exemplo, A fórmula de Euler) estão, de novo, elegante quando os argumentos das funções estão em radianos e confuso contrário.

Análise dimensional

Embora o radiano é uma unidade de medida, é uma quantidade adimensional. Isto pode ser visto a partir da definição dada anteriormente: o ângulo subtendido no centro de um círculo, medido em radianos, é a razão entre o comprimento do arco fechado para o comprimento do raio do círculo. Uma vez que as unidades de medida cancelar, esta proporção é adimensional.

Outra maneira de ver a dimensionlessness do radiano é nas representações da série das funções trigonométricas, como a série de Taylor para sen x mencionado anteriormente:

Se x tinha unidades, então a soma teria sentido: o termo x linear não pode ser adicionada à (ou ter subtraído) o termo cúbico 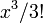ou o termo quintic 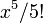, Etc. Assim, x deve ser adimensional.

Use em física

O radiano é amplamente utilizado em física quando são necessárias medições angulares. Por exemplo, a velocidade angular é normalmente medido em radianos por segundo (rad / s). Uma revolução por segundo é igual a 2π radianos por segundo.

Da mesma forma, aceleração angular é medida em radianos por segundo por segundo (rad / s ^2).

As razões são as mesmas que em matemática.

Múltiplos de unidades radian

Prefixos métricos têm uso limitado com radianos, e nenhum em matemática.

O miliradiano (0,001 rad, ou de 1 mrad) é usado em e artilharia segmentação, porque ele corresponde a um erro de 1 m, a uma gama de 1,000 m (em ângulos tão pequenos, a curvatura é negligenciável). O divergência de laser de raios também é geralmente medida em miliradianos.

Unidades menores, como microrradianos (μrads) e nanoradians (nrads) são usados em astronomia, e também pode ser utilizado para medir a qualidade do feixe de laser com ultra-baixa divergência. Da mesma forma, os prefixos menor do que milli- são potencialmente úteis na medição extremamente pequenos ângulos.

No entanto, os prefixos maiores têm nenhuma utilidade aparente, principalmente porque a exceder 2π radianos é começar do mesmo círculo (ou ciclo revolucionário) novamente.