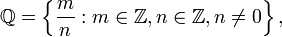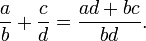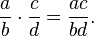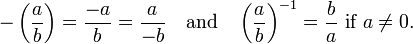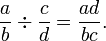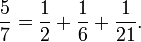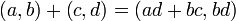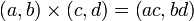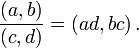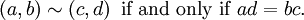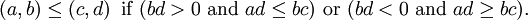Número racional

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/

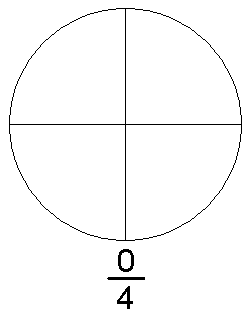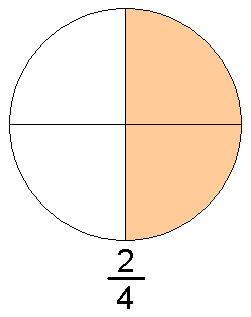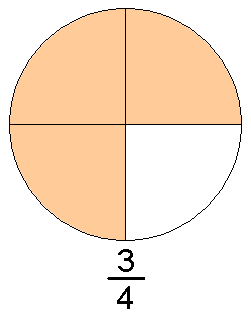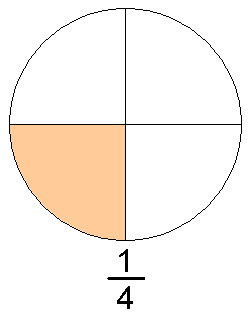
Em matemática , um número racional é um número que pode ser expresso como um razão de dois inteiros . Números racionais não inteiros (comumente chamados de frações ) são geralmente escritos como a fração vulgar 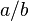$a / b$ , Onde b é não nula . um é chamado o numerador , e B, o denominador .

Cada número racional pode ser escrita em um número infinito de formas, tais como 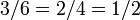$3/6 = 2/4 = 1/2$ , Mas diz-se estar na forma mais simples, quando a e b não têm comuns divisores excepto 1 (isto é, eles são coprime). Todo número racional diferente de zero tem exatamente uma forma mais simples deste tipo com um denominador positivo. Uma fracção desta forma mais simples é dito ser um fração irredutível, ou uma fracção em forma reduzida.

O expansão de um número decimal é racional periódica eventualmente (no caso de uma expansão finito os zeros que, implicitamente, o seguem formar a parte periódica). O mesmo é verdadeiro para qualquer outra base integrante acima de um, e é também verdade quando os números racionais são considerados números p-adic em vez de números reais . Por outro lado, se a expansão de um número por uma base é periódica, é periódica para todas as bases e é o número racional. Um número real que não é um número racional, é chamado um número irracional .

Alojamento

O conjunto de todos os números racionais, que constitui um campo, é denotada 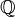$\ Mathbb {Q}$ . Usando o notação set-construtor, 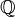$\ Mathbb {Q}$ é definido como

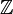$\ Mathbb {Q} = \ \ left {\ frac {m} {n}: m \ in \ mathbb {Z}, n \ in \ mathbb {Z}, n \ ne 0 \ right \},$

onde $\ Mathbb {Z}$ denota o conjunto de números inteiros.

O termo racional

No mundo matemático, o adjetivo racional, muitas vezes significa que o subjacente considerado campo é o campo 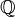$\ Mathbb {Q}$ números de racional. Por exemplo, um número inteiro racional é um algébrica inteiro que também é um número racional, o que quer dizer, um número inteiro ordinária, e uma matriz racional é uma matriz cujos coeficientes são números racionais. Polinomial racional normalmente, e mais corretamente, significa um polinômio com coeficientes racionais, também chamado de "polinômio sobre os números racionais". No entanto, função racional não significa que o campo subjacente são os números racionais, e uma curva algébrica racional não é uma curva algébrica com coeficientes racionais.

Aritmética

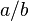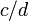Dois números racionais $a / b$ e $c / d$ são iguais se e apenas se $ad = bc$ .

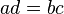Duas fracções são adicionados como se segue

$\ Frac {a} {b} + \ frac {c} {d} = \ frac {ad + bc} {} bd.$

A regra para a multiplicação é

$\ Frac {a} {b} \ cdot \ frac {c} {d} = \ frac {} {ac bd}.$

Aditivo e inversos multiplicativos existe nos números racionais

$- \ Left (\ frac {a} {b} \ right) = \ frac {-a} {b} = \ frac {a} {- b} \ quad \ mbox {e} \ quad \ left (\ frac { a} {b} \ right) ^ {- 1} = \ frac {b} {a} \ mbox {if} a \ neq 0.$

Segue-se que o quociente de duas fracções é dado pela

$\ Frac {a} {b} \ div \ frac {c} {d} = \ frac {} {bc ad}.$

Fracções egípcias

Qualquer número racional positivo pode ser expresso como uma soma de distinto recíprocos de inteiros positivos, tais como

$\ Frac {5} {7} = \ frac {1} {2} + \ frac {1} {6} + \ frac {1} {21}.$

Para qualquer número racional positivo, há uma infinidade de diferentes tais representações, chamadas Fracções egípcias, como eles foram usados pelo antigo Egípcios. Os egípcios também tinham uma notação diferente para fracções diádicas.

Construção formal

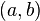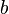Matematicamente podemos construir os números racionais como classes de equivalência de pares ordenados de números inteiros $\ Left (a, b \ right)$ , Com $b$ não é igual a zero. Podemos definir adição e multiplicação destes pares com as seguintes regras:

$\ Left (a, b \ right) + \ left (c, d \ right) = \ left (ad + bc, bd \ right)$

$\ Left (a, b \ right) \ times \ left (c, d \ right) = \ left (ac, bd \ right)$

e se c ≠ 0, por divisão

$\ Frac {\ left (a, b \ right)} {\ left (c, d \ right)} = \ left (ad, bc \ right).$

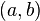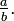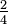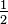A intuição é que $\ Left (a, b \ right)$ representa o número denotado por a fracção $\ Tfrac {a} {b}.$ Para estar em conformidade com a nossa expectativa de que $\ Tfrac {2} {4}$ e $\ Tfrac {1} {2}$ denotam o mesmo número, que define uma relação de equivalência 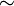$\ Sim$ sobre esses pares com a seguinte regra:

$\ Left (a, b \ right) \ sim \ left (c, d \ right) \ mbox {se e somente se ad = bc}.$

Esta relação de equivalência é uma relação de congruência: é compatível com a adição e multiplicação definido acima, e que podem definir Q ser a conjunto quociente de ~, ou seja, nós identificamos dois pares (a, b) e (c, d) se eles são equivalentes no sentido acima. (Esta construção pode ser realizada de qualquer domínio integral: ver campo de fracções).

Nós também podemos definir uma ordem total sobre Q por escrito

$\ Left (a, b \ right) \ le \ left (c, d \ right) \ mbox {if} (bd> 0 \ mbox {} e ad \ le bc) \ mbox {} ou (bd <0 \ mbox {} e ad \ ge bc).$

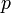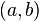Os inteiros podem ser considerados como números racionais por o que a incorporação de mapas $p \,$ para $[(P, 1)], \,$ onde $[(A, b)] \,$ denota a classe de equivalência tendo $(A, b) \,$ como membro.

Propriedades

um diagrama que ilustra o countabililty dos racionais

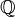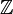O conjunto $\ Mathbb {Q}$ , Em conjunto com as operações de adição e multiplicação mostrados acima, constitui um campo, o campo de fracções dos inteiros $\ Mathbb {Z}$ .

Os racionais são o menor campo com característica zero: todos os outros campos de característica zero contém uma cópia do 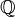$\ Mathbb {Q}$ . Os números são racionais, por conseguinte, o campo privilegiado para característica zero.

O fecho algébrico de 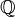$\ Mathbb {Q}$ , Isto é, o campo de raizes de polinómios racionais, é a números algébricos.

O conjunto de todos os números racionais é contável. Uma vez que o conjunto de todos os números reais é incontável, dizemos que quase todos os números reais são irracionais, no sentido de Medida de Lebesgue, ou seja, o conjunto dos números racionais é um conjunto nulo.

Os racionais são um densamente ordenou conjunto: entre quaisquer dois racionais, não fica outro, de fato infinitamente muitos outros. Qualquer totalmente ordenado conjunto que é contável, densa (no sentido acima), e não tem nenhum elemento menos ou maior é ordem isomorphic aos números racionais.

Números reais e propriedades topológicas das rationals

Os racionais são um subconjunto denso dos números reais: cada número real tem números racionais arbitrariamente próximo a ele. Uma propriedade relacionada é que os números racionais são os únicos números com expansões finitas como frações contínuas regulares.

Em virtude da sua ordem, os racionais carregam uma topologia de ordem. Os números racionais também carregam uma topologia subespaço. Os números racionais formar um espaço métrico usando a métrica d (x, y) = | x - y |, e isto produz uma terceira topologia sobre 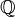$\ Mathbb {Q}$ . Todos os três topologias coincidem e transformar os racionais em um campo topológico. Os números racionais é um exemplo importante de um espaço que não é localmente compacto. Os racionais são caracterizados topologicamente como o único contável espaço sem metrizável pontos isolados. O espaço é também totalmente desconectado. 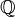Os números racionais não formam um completar espaço métrico; os números reais são a conclusão de $\ Mathbb {Q}$ .

p números -adic

Além da métrica valor absoluto mencionado acima, existem outras métricas que se transformam 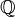$\ Mathbb {Q}$ em um campo topológico:

Deixar 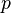$p$ ser um número primo e para qualquer inteiro diferente de zero 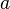$um$ deixar 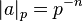$| A | _p = p ^ {- n}$ , Onde 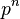$p ^ n$ é o mais alto poder de 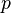$p$ divisória $um$ ;

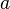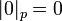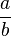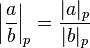Além gravação $| 0 | _p = 0$ . Para qualquer número racional $\ Frac {a} {b}$ , Definimos $\ Left | \ frac {a} {b} \ right | _p = \ frac {| a | _p} {| b | _p}$ .

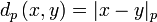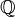Em seguida $D_P \ left (x, y \ right) = | x - y | _p$ define um métrica em $\ Mathbb {Q}$ .

O espaço métrico 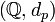$\ Left (\ mathbb {Q}, D_P \ right)$ não é completa, e a sua conclusão é a p campo de número -adic 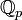$\ Mathbb {Q} _p$ . Teorema de Ostrowski afirma que qualquer não-trivial valor absoluto sobre os números racionais 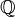$\ Mathbb {Q}$ é equivalente ao valor absoluto ou o verdadeiro habitual ou um p-adic valor absoluto.

Retirado de " http://en.wikipedia.org/w/index.php?title=Rational_number&oldid=199219044 "