
Limite de Roche
Fundo para as escolas Wikipédia
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. SOS mães cada um cuidar de uma família de crianças apadrinhadas .

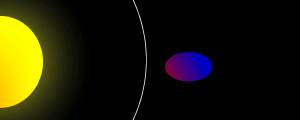


O limite de Roche ( / ʁoʃ /), por vezes referido como o raio Roche, é a distância em que um corpo celeste, realizada em conjunto apenas pela sua própria gravidade , vai se desintegrar devido a um segundo corpo celeste forças de maré gravitacional superiores a auto-atração do primeiro corpo. Dentro do limite de Roche, material de órbita tenderá a dispersar e forma anéis, enquanto fora do limite, material tenderá a aglutinam. O termo é nomeado após Édouard Roche, o francês astrônomo que primeiro calculado este limite teórico em 1848.
Explicação
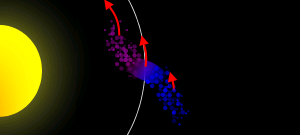
Tipicamente, o limite de Roche aplica-se a um desintegração via satélite devido à força das marés induzidas por seu primário, o corpo sobre o qual órbitas. Partes do satélite que estão mais perto do principal são atraídos pela gravidade mais forte do primário, enquanto que partes mais distantes são repelidos por forte a força centrífuga a partir de curva da órbita de satélite. Alguns satélites reais, tanto natural e artificial, pode orbitar dentro de seus limites Roche porque eles são mantidos juntos por outros do que a gravitação. forças Júpiter lua 's Metis e Saturno Lua 's Pan são exemplos de tais satélites, que prendem em conjunto por causa da sua resistência à tracção (ou seja, eles são sólidos e não facilmente puxado para além). Em casos extremos, os objectos que descansa sobre a superfície de um tal satélite poderia realmente ser levantada pelas forças gravitacionais. Um satélite mais fraca, tal como um cometa , poderia ser dividido quando se passa dentro do seu limite de Roche.
Desde forças de maré sobrecarregar a gravidade que possam manter o satélite em conjunto dentro do limite de Roche, nenhuma grande satélite pode gravitacionalmente aglutinam de partículas menores dentro desse limite. De facto, quase todos conhecidos anéis planetários estão localizados dentro de seu limite de Roche, Saturno E-Ring e Anel de Phoebe sendo exceções notáveis. Eles poderiam ser tanto de restos do planeta proto-planetário disco de acreção que não conseguiu se aglutinam em pequenas luas, ou, inversamente, ter-se formado quando uma lua passou dentro do seu limite Roche e se separaram.
Também vale a pena considerar que o limite de Roche não é o único fator que faz com que os cometas se quebre. Dividindo por estresse térmico, interno pressão do gás e divisão de rotação são maneiras mais prováveis para um cometa para dividir sob estresse.
Determinar o limite de Roche
A distância a que a limitação de um satélite pode aproximar-se sem se romper depende da rigidez do satélite. Em um extremo, um satélite completamente rígida vai manter a sua forma até que as forças de maré fragmentá-lo. No outro extremo, um satélite altamente fluido gradualmente deforma que conduz ao aumento das forças de maré, fazendo com que o satélite para alongar, agravando ainda mais as forças de maré e fazendo-a quebrar mais facilmente. A maioria dos satélites reais estaria em algum lugar entre esses dois extremos, com resistência à tração tornando o satélite nem perfeitamente rígida nem perfeitamente fluido. O limite de Roche também é geralmente calculado para o caso de uma órbita circular, embora seja fácil de alterar o cálculo a aplicar para o processo (por exemplo) de um corpo de passagem do primário numa trajectória parabólica ou hiperbólica.
Cálculo rígida-satélite
O limite de Roche de corpo rígido é um cálculo simplificado para um satélite esférica, em que a deformação do corpo por efeitos de maré é negligenciado. O corpo é assumido para manter a sua esférico forma enquanto está sendo realizada em conjunto apenas pela sua própria auto-gravidade. Outros efeitos também são negligenciadas, tais como a deformação da corrente primária, e a rotação da órbita do satélite, e a sua forma irregular. Estes pressupostos, embora irrealista, simplificar muito o cálculo Roche-limite.
O limite de Roche para um satélite esférica rígida excluindo efeitos orbitais, é a distância, 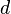 , A partir do primário em que a força gravitacional sobre a massa de ensaio sobre a superfície do objecto é exactamente igual à força de maré puxar o objecto para longe do objecto:
, A partir do primário em que a força gravitacional sobre a massa de ensaio sobre a superfície do objecto é exactamente igual à força de maré puxar o objecto para longe do objecto:
onde 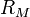 é o raio do primário,
é o raio do primário, 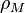 representa a densidade do primário, e
representa a densidade do primário, e 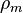 é a densidade do satélite. Isto pode ser escrito como equivalentemente
é a densidade do satélite. Isto pode ser escrito como equivalentemente
onde 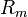 é o raio do secundário,
é o raio do secundário, 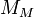 é a massa do primário, e
é a massa do primário, e 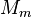 é a massa do secundário.
é a massa do secundário.
Note que este não depende de quão grande é o objeto em órbita é, mas apenas na relação de densidades. Esta é a distância orbital no interior do qual material a granel (por exemplo, regolith ou rochas soltas) sobre a superfície do satélite mais próximo do primário será puxado para fora, e do mesmo modo sobre o material do lado oposto ao do primário será também puxado para fora a partir de, em vez de para, o satélite.
Se o satélite é mais de duas vezes tão denso como o primário, como pode facilmente ser o caso de uma lua rochoso que orbita um gigante de gás, o limite de Roche estará dentro do primário e, portanto, não é relevante.
Derivação da fórmula
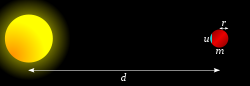
A fim de determinar o limite de Roche, considera-se uma massa pequena 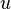 sobre a superfície do satélite mais próximo do primário. Existem duas forças nesta massa
sobre a superfície do satélite mais próximo do primário. Existem duas forças nesta massa 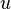 : A atração gravitacional para o satélite ea força gravitacional para o primário. Assumindo que o satélite está em queda livre em torno do primário e que o força de maré é o único termo relevante da atração gravitacional do primário. Esta suposição é uma simplificação como de queda livre só é verdadeiramente se aplica ao centro planetário, mas será suficiente para essa derivação.
: A atração gravitacional para o satélite ea força gravitacional para o primário. Assumindo que o satélite está em queda livre em torno do primário e que o força de maré é o único termo relevante da atração gravitacional do primário. Esta suposição é uma simplificação como de queda livre só é verdadeiramente se aplica ao centro planetário, mas será suficiente para essa derivação.
A atração gravitacional 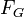 na massa
na massa 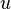 para o satélite com massa
para o satélite com massa 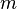 e raio
e raio  pode ser expresso de acordo com a Lei da gravitação de Newton.
pode ser expresso de acordo com a Lei da gravitação de Newton.
o força de maré 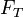 na massa
na massa 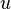 para o primário com raio
para o primário com raio 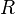 e massa
e massa 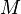 , A uma distância
, A uma distância 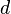 entre os centros dos dois corpos, pode ser expresso como aproximadamente
entre os centros dos dois corpos, pode ser expresso como aproximadamente
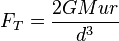 .
.
Para obter esta aproximação, determinar a diferença na força gravitacional do primário no centro do satélite e na extremidade mais próxima do satélite para o primário:
Na aproximação em que r < 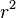 no numerador e cada termo com
no numerador e cada termo com  no denominador vai a zero, o que nos dá:
no denominador vai a zero, o que nos dá:
O limite de Roche é alcançado quando a força gravitacional ea força de maré equilibrar-se mutuamente.
ou
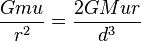 ,
,
que dá o limite de Roche, 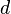 , Conforme
, Conforme
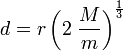 .
.
No entanto, nós realmente não quer o raio do satélite para aparecer na expressão para o limite, portanto, re-escrever este em termos de densidades.
Para uma esfera da massa 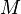 pode ser escrita como
pode ser escrita como
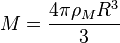 onde
onde 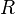 é o raio do primário.
é o raio do primário.
E da mesma forma
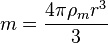 onde
onde  é o raio do satélite.
é o raio do satélite.
Substituindo para as massas na equação para o limite de Roche, e anulando 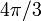 dá
dá
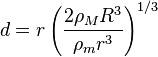 ,
,
que pode ser simplificado para o limite de Roche:
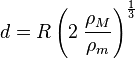 .
.
Satélites Fluidos
Uma abordagem mais precisa para o cálculo do limite de Roche leva a deformação do satélite em conta. Um exemplo seria um extremo tidally bloqueado por satélite líquido orbitando um planeta, onde nenhuma força atuando sobre o satélite iria deformar-lo em um prolate esferóide.
O cálculo é complexo e não o seu resultado pode ser representado numa fórmula algébrico exacto. Roche próprio derivado a seguinte solução aproximada para o limite de Roche:
No entanto, uma melhor aproximação que leva em conta achatamento do primário e de massa do satélite é:
onde 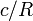 é o achatamento do primário. O factor numérico é calculado com o auxílio de um computador.
é o achatamento do primário. O factor numérico é calculado com o auxílio de um computador.
A solução do fluido é apropriado para organismos que são mantidas unidas apenas vagamente, tal como um cometa. Por exemplo, cometa Decadente órbita de Shoemaker-Levy 9 em torno de Júpiter passou dentro de seu limite de Roche em Julho de 1992, fazendo-o fragmento em um número de peças menores. Em sua próxima abordagem, em 1994, os fragmentos caiu no planeta. Shoemaker-Levy 9 foi observada pela primeira vez em 1993, mas sua órbita indicou que tinha sido capturado por Júpiter algumas décadas antes.
Derivação da fórmula
Como o caso satélite fluido é mais delicada do que a rígida, o satélite é descrito com algumas hipóteses simplificadoras. Em primeiro lugar, assumir o objecto consiste em fluido incompressível que tem densidade constante 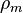 e o volume
e o volume 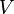 que não dependem de forças externas ou internas.
que não dependem de forças externas ou internas.
Em segundo lugar, assumir o satélite se move em uma órbita circular e permanece em rotação síncrona. Isto significa que a velocidade angular 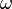 em que ele gira em torno do seu centro de massa é a mesma que a velocidade angular em que se move em torno do sistema global baricentro.
em que ele gira em torno do seu centro de massa é a mesma que a velocidade angular em que se move em torno do sistema global baricentro.
A velocidade angular 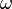 é dado pela terceira lei de Kepler :
é dado pela terceira lei de Kepler :
Quando M é muito maior do que m, esta será perto de
A rotação sincronizada implica que o líquido não se move e o problema pode ser considerado como um estático. Portanto, o viscosidade e o atrito do líquido neste modelo não desempenham um papel, uma vez que estas quantidades que desempenham um papel apenas para um fluido em movimento.
Tendo em conta estas premissas, os seguintes forças devem ser tidas em conta:
- A força da gravidade, devido ao corpo principal;
- o força centrífuga no sistema de referência rotativo; e
- o campo auto-gravitação do satélite.
Uma vez que todas estas forças são conservadoras, que pode ser expressa por meio de um potencial. Além disso, a superfície do satélite é um um equipotencial. Caso contrário, as diferenças de potencial iria dar origem a forças de movimento e de algumas partes do líquido na superfície, o que contraria o pressuposto modelo estático. Dada a distância a partir do corpo principal, o problema é determinar a forma da superfície que satisfaça a condição equipotencial.
À medida que a órbita foi assumido circular, a força gravitacional total e a força centrífuga que actua no corpo principal cancelar. Portanto, a força que afecta as partículas do líquido é a força das marés, o qual depende da posição em relação ao centro de massa, já considerado no modelo rígido. Para corpos pequenos, a distância das partículas de líquido a partir do centro do corpo é pequena em relação à distância d para o corpo principal. Assim, a força de maré pode ser linearizado, resultante da mesma fórmula para F T como indicado acima. Enquanto esta força no modelo rígido depende apenas do raio r do satélite, no caso de líquidos temos de considerar todos os pontos da superfície e da força de corrente depende da distância Δd do centro de massa de uma dada partícula projectada na linha que une o satélite e o corpo principal. Chamamos Δd a distância radial. Uma vez que a força de maré é linear em Δd, o potencial relacionado é proporcional ao quadrado da variável e para 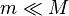 temos
temos
Queremos determinar a forma do satélite para os quais a soma do potencial de auto-gravitação e 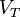 é constante sobre a superfície do corpo. Em geral, um tal problema é muito difícil de resolver, mas neste caso específico, pode ser resolvido por uma suposição hábil devido à dependência quadrado do potencial de corrente em que a distância radial Δd
é constante sobre a superfície do corpo. Em geral, um tal problema é muito difícil de resolver, mas neste caso específico, pode ser resolvido por uma suposição hábil devido à dependência quadrado do potencial de corrente em que a distância radial Δd
Uma vez que o potencial V T muda apenas numa direcção, isto é, a direcção do corpo principal, o satélite pode-se esperar que tomam uma forma axialmente simétrica. Mais precisamente, podemos assumir que é preciso uma forma de sólido de revolução. A auto-potencial na superfície de tal forma de um sólido de revolução só pode depender da distância radial ao centro de massa. Na verdade, o cruzamento do satélite e um plano perpendicular à linha que une os organismos é um disco cujo limite por nossas suposições é um círculo de potencial constante. No caso de a diferença entre o potencial V e auto-gravitação t ser uma constante, ambos os potenciais deve depender da mesma maneira em Δd. Em outras palavras, a auto-potencial tem de ser proporcional ao quadrado da Δd. Em seguida, pode-se mostrar que a solução equipotential é um elipsóide de revolução. Dada uma densidade e volume constante do potencial de auto-tal corpo depende apenas da excentricidade ε do elipsóide:
onde 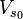 é a auto-potencial constante na intersecção da aresta circular do corpo e o plano central de simetria dado pela equação Δd = 0.
é a auto-potencial constante na intersecção da aresta circular do corpo e o plano central de simetria dado pela equação Δd = 0.
A função adimensional f é para ser determinada a partir da solução precisas para o potencial do elipsóide
e, surpreendentemente, não depende do volume do satélite.
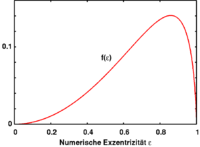
Embora a forma explícita da função f olha complicado, é claro que podem e não escolher o valor de ε de modo a que o potencial V T é igual a V S mais uma constante independente da variável Δd. Por inspeção, isso ocorre quando
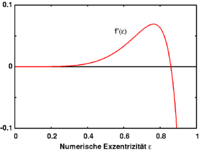
Esta equação pode ser resolvida numericamente. O gráfico indica que há duas soluções e, assim, o menor representa a forma de equilíbrio estável (a elipsóide com a excentricidade menor). Esta solução determina a excentricidade do elipsóide corrente como uma função da distância ao corpo principal. A derivada da função f tem um zero onde a excentricidade máxima é alcançada. Isto corresponde ao limite de Roche.
Mais precisamente, o limite de Roche é determinado pelo facto de que a função f, que pode ser considerado como uma medida linear da força de compressão do elipsóide para uma forma esférica, é limitada para que não haja uma excentricidade em que este se torne máxima força de contração . Uma vez que a força de corrente aumenta quando o satélite se aproxima do corpo principal, é evidente que existe uma distância crítica em que o elipsóide está rasgado.
A excentricidade máxima pode ser calculado numericamente como o zero do derivado de f '. Obtém-se
que corresponde à relação do elipsóide eixos 1: 1,95. A inserção deste na fórmula para a função f pode-se determinar a distância mínima na qual existe a elipsóide. Este é o limite de Roche,
Roche limites para exemplos selecionados
A tabela abaixo mostra a densidade média e o raio equatorial de objetos selecionados no Sistema Solar .
| Primário | Densidade (kg / m³) | Raio (m) |
|---|---|---|
| Sol | 1408 | 696000000 |
| Júpiter | 1326 | 71492000 |
| Terra | 5513 | 6378137 |
| Lua | 3346 | 1738100 |
| Saturno | 687 | 60268000 |
| Urano | 1318 | 25559000 |
| Netuno | 1638 | 24764000 |
Usando esses dados, os limites da Roche para corpos rígidos e fluido pode ser facilmente calculado. A densidade média de cometas é considerado como sendo cerca de 500 kg / m³.
A tabela abaixo apresenta os limites Roche expressos em metros e em raios primário. O limite de Roche verdadeiro para um satélite depende da sua densidade e rigidez.
| Corpo | Satélite | Limite de Roche (rígida) | Limite de Roche (líquido) | ||
|---|---|---|---|---|---|
| Distância (km) | R | Distância (km) | R | ||
| Terra | Lua | 9496 | 1.49 | 18.261 | 2.86 |
| Terra | cometa média | 17.880 | 2.80 | 34.390 | 5.39 |
| Sol | Terra | 554400 | 0.80 | 1066300 | 1.53 |
| Sol | Júpiter | 890700 | 1.28 | 1713000 | 2.46 |
| Sol | Lua | 655300 | 0.94 | 1260300 | 1.81 |
| Sol | cometa média | 1234000 | 1.78 | 2374000 | 3,42 |
Se o primário é menos da metade tão denso quanto o satélite, o limite de Roche de corpo rígido é menor que o raio do primário, e os dois corpos podem colidir antes do limite de Roche é atingido.
O quão perto estão as luas do Sistema Solar para seus limites Roche? A tabela abaixo dá raio da órbita de cada satélite interior dividido por seu próprio raio Roche. Ambos cálculos de corpo rígido e fluidos são dadas. Nota Pan, Metis, e Naiad, em particular, o que pode ser bastante próximo de seus pontos de break-up reais.
Na prática, as densidades da maioria dos satélites internos de planetas gigantes não são conhecidos. Nestes casos, mostrado em itálico, valores susceptíveis têm sido assumido, mas o seu limite real Roche pode variar desde o valor indicado.
| Primário | Satélite | Limite Orbital Radius / Roche | |
|---|---|---|---|
| (Rígida) | (Fluido) | ||
| Sol | Mercúrio | 104: 1 | 54: 1 |
| Terra | Lua | 41: 1 | 21: 1 |
| Marte | Phobos | 172% | 89% |
| Deimos | 451% | 234% | |
| Júpiter | Mestiço | ~ 186% | ~ 94% |
| Adrástea | ~ 188% | ~ 95% | |
| Amalthea | 175% | 88% | |
| Tebe | 254% | 128% | |
| Saturno | Panela | 142% | 70% |
| Atlas | 156% | 78% | |
| Prometeu | 162% | 80% | |
| Pandora | 167% | 83% | |
| Epimeteu | 200% | 99% | |
| Jano | 195% | 97% | |
| Urano | Cordelia | ~ 154% | ~ 79% |
| Ophelia | ~ 166% | ~ 86% | |
| Bianca | ~ 183% | ~ 94% | |
| Cressida | ~ 191% | ~ 98% | |
| Desdemona | ~ 194% | ~ 100% | |
| Juliet | ~ 199% | ~ 102% | |
| Netuno | Náiade | ~ 139% | ~ 72% |
| Thalassa | ~ 145% | ~ 75% | |
| Despina | ~ 152% | ~ 78% | |
| Galatea | 153% | 79% | |
| Larissa | ~ 218% | ~ 113% | |
| Plutão | Charon | 12,5: 1 | 6.5: 1 |

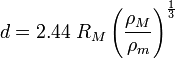
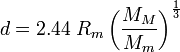
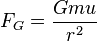
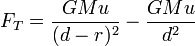
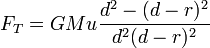
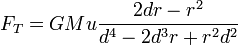
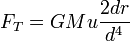
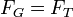
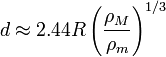
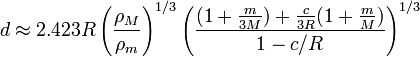
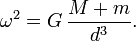
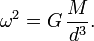

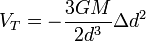
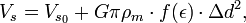
![f (\ epsilon) = \ frac {1 - \ epsilon ^ 2} {\ epsilon ^ 3} \ cdot \ left [\ left (3- \ epsilon ^ 2 \ right) \ cdot \ mathrm {arcsinh} \ left (\ frac {\ epsilon} {\ sqrt {1- \ epsilon ^ 2}} \ right) -3 \ epsilon \ right]](../../images/1502/150266.png)
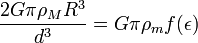
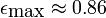
![d \ approx 2 {.} 423 \ cdot R \ cdot \ sqrt [3] {\ frac {\ rho_M} {\ rho_m}} \ ,.](../../images/1502/150277.png)
