
Simetria
Fundo para as escolas Wikipédia
Crianças SOS têm produzido uma seleção de artigos da Wikipédia para escolas desde 2005. Crianças SOS é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.
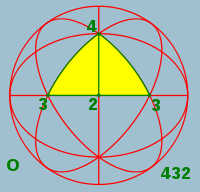
Simétrica no uso comum geralmente transmite dois significados primários. O primeiro é um sentido impreciso da proporcionalidade e equilíbrio harmonioso ou esteticamente agradável; de tal forma que ele reflete a beleza ou perfeição. O segundo significado é um conceito preciso e bem definido de equilíbrio ou "modelado auto-similaridade" que pode ser demonstrada ou provada de acordo com as regras de um sistema formal: por geometria , através de física ou de outra forma.
Embora os significados são distinguíveis, em alguns contextos, ambos os significados de "simetria" estão relacionadas e discutido em paralelo.
As noções "preciso" de simetria tem várias medidas e definições operacionais. Por exemplo, a simetria pode ser observado:
- no que diz respeito à passagem do tempo ;
- como uma relação espacial;
- através geométrica tais como transformações dimensionamento, reflexão, e rotação;
- através de outros tipos de transformações funcionais; e
- como um aspecto objetos abstratos, modelos teóricos, língua , música e até mesmo o próprio conhecimento.
Este artigo descreve essas noções de simetria a partir de três perspectivas. A primeira é a de matemática , em que são definidas as simetrias e categorizadas com precisão. A segunda perspectiva descreve simetria que se refere à ciência e tecnologia . Neste contexto, simetrias subjacentes a alguns dos resultados mais profundos da moderna física , incluindo os aspectos de espaço e tempo. Finalmente, uma terceira perspectiva discute simetria nas humanidades , cobrindo seu uso rico e variado na história , arquitetura , arte e religião .
O oposto de simetria é assimetria.
Simetria em matemática
Em termos formais, dizemos que um objecto é simétrico em relação a um dado operação matemática, se, quando aplicada ao objeto, esta operação não altera o objeto ou a sua aparência. Dois objectos são simétricas uma à outra em relação a um determinado grupo de operações se for obtida a partir da outra por algumas das operações (e vice-versa).
Simetrias pode também ser encontrada em organismos vivos incluindo seres humanos e outros animais (ver simetria bilateral abaixo). Na geometria 2D os principais tipos de simetria de interesse são com respeito à base Isometries plano euclidiano: traduções, rotações, reflexões, e deslizar reflexões.
Modelo matemático para simetria
O conjunto de todas as operações de simetria considerado, em todos os objetos em um conjunto X, pode ser modelado como uma a ação do grupo g: G × X → X, onde a imagem de g em G e x em X é escrita como g · x. Se, por algum g, g · x = y então x e y são ditos ser simétricas uma à outra. Para cada objecto X, para o qual as operações de g g-x = x formam um grupo , o grupo de simetria do objecto, um subgrupo de G. Se o grupo de simetria X é o grupo trivial então x é dito para ser assimétrica, de outra forma simétrica. Um exemplo geral é que G é um grupo de bijeções g: V → V agindo sobre o conjunto de funções x: V → W por (gx) (V) = x (g -1 (v)) (ou um conjunto restrito de tais funções de que é fechado sob a ação do grupo). Assim, um grupo de bijeções de espaço induz uma ação de grupo em "objetos" na mesma. O grupo de simetria x consiste de todos g para o qual x (v) = x (G (v)) para todos v. G é o grupo de simetria do próprio espaço, e de qualquer objecto que é uniforme ao longo do espaço. Alguns subgrupos de G não pode ser o grupo de simetria de qualquer objecto. Por exemplo, se o grupo contém para cada v e w em V de tal forma que um g G (V) = W, em seguida, apenas os grupos de simetria de funções constante de x que contêm grupo. No entanto, o grupo de simetria de funções constante é a própria L.
Numa versão modificada para campos vectoriais, temos (GX) (v) = h (x g, (g-1 (v))), onde h gira quaisquer vectores e pseudovectors em x, e inverte quaisquer vectores (mas não pseudovectors) de acordo com a rotação e inversão em g, ver simetria na física. O grupo de simetria x consiste de todos g para o qual X (v) = h (g, x (G (V))) para todos v. Neste caso, o grupo de simetria de uma função constante pode ser um subgrupo adequada de L: um vector constante tem apenas simetria de rotação em relação à rotação em torno de um eixo, se é que o eixo no sentido do vector, e só se simetria de inversão é zero.
Para uma noção comum de simetria no espaço euclidiano , G é o Grupo euclidiana e (n), o grupo de isometries, e V é o espaço euclidiano. O grupo de um objecto de rotação é o grupo de simetria se G é restrito para E + (N), o grupo de isometries directos. (Para generalizações, consulte a próxima subseção.) Os objetos podem ser modeladas como funções x, dos quais um valor pode representar uma seleção de propriedades como cor, densidade, composição química, etc. Dependendo da selecção considerarmos apenas simetrias de conjuntos de pontos (x é apenas um função booleana de posição v), ou, no outro extremo, por exemplo, a simetria da mão direita e esquerda com toda a sua estrutura.
Para um dado grupo de simetria, as propriedades da parte do objecto, definir completamente todo o objecto. Considerando pontos equivalente que, devido à simetria, têm as mesmas propriedades, os classes de equivalência são os órbitas da ação do grupo no próprio espaço. Precisamos do valor de x em um ponto em cada órbita para definir o objeto inteiro. Um conjunto de tais representantes forma uma domínio fundamental. O menor domínio essencial não tem uma simetria; neste sentido, pode-se dizer que a simetria dependa assimetria.
Um objecto com uma simetria desejado pode ser produzido por escolha para cada órbita um único valor de função. A partir de um determinado objeto x que pudermos por exemplo:
- tomar os valores em um domínio fundamental (ou seja, adicionar cópias do objeto)
- tomar para cada órbita algum tipo de média ou a soma dos valores de x, nos pontos da órbita (idem, em que as cópias possam sobrepor)
Se for desejado não ter mais do que a simetria do grupo de simetria, em seguida, o objecto a ser copiado deve ser assimétrica.
Como indicado acima, alguns grupos de isometrias não são o grupo de simetria de qualquer objeto, exceto no modelo modificado para campos vetoriais. Por exemplo, isto aplica-se em 1D para o grupo de todas as traduções. O domínio fundamental é apenas um ponto, por isso não podemos torná-lo assimétrica, portanto, qualquer "padrão" invariante sob a tradução também é invariante sob reflexão (estes são os "padrões" uniformes).
Na versão campo vectorial simetria de translação contínuo não implica simetria reflectional: o valor da função é constante, mas se ele contém vectores diferentes de zero, não existe qualquer simetria reflectional. Se também houver simetria reflectional, o valor da função constante não contém vetores diferentes de zero, mas pode conter pseudovectors diferentes de zero. Um exemplo 3D correspondente é um infinito cilindro com uma corrente perpendicular ao eixo; o campo magnético (a pseudovetor) é, na direcção do cilindro, constante, mas diferente de zero. Para vectores (em particular o densidade de corrente) que tem simetria em cada plano perpendicular ao do cilindro, bem como simetria cilíndrica. Esta simetria cilíndrica espelho sem planos através do eixo também só é possível na versão campo vetorial do conceito de simetria. Um exemplo semelhante é um cilindro que gira em torno do seu eixo, em que o campo magnético e densidade de corrente são substituídos por momento angular e velocidade , respectivamente.
Um grupo de simetria é dito para agir sobre um recurso transitively repetida de um objecto se, para cada par de ocorrências da característica não é uma operação de simetria mapeamento do primeiro para o segundo. Por exemplo, em 1D, o grupo de simetria de {..., 1,2,5,6,9,10,13,14, ...} transitively actua em todos estes pontos, enquanto {..., 1, 2,3,5,6,7,9,10,11,13,14,15, ...} não actua transitively em todos os pontos. Equivalentemente, o primeiro conjunto é apenas um classe de conjugação no que respeita ao isometries, enquanto a segunda tem duas classes.
Simetria não isométrico
Como mencionado acima, G (o grupo de simetria do próprio espaço) pode ser diferente da Grupo euclidiana, o grupo de isometries.
Exemplos:
- G é o grupo de transformações de similaridade, ou seja, transformações afins com uma matriz A que é um vezes um escalares matriz ortogonal. Assim dilatações são adicionados, auto-semelhança é considerada uma simetria
- G é o grupo de transformações afins com uma matriz com um determinante 1 ou -1, ou seja, a transformação que preservam área; isto adiciona por exemplo oblíqua simetria de reflexão.
- G é o grupo de todas as transformações afins bijective
- Em geometria inversiva, G inclui reflexões círculo, etc.
- Em termos mais gerais, uma involução define uma simetria em relação a que a involução.
Simetria direcional
Ver simetria direcional.
Simetria de reflexão
Ver simetria de reflexão.
Simetria reflexão, espelho simetria, espelho de imagem simetria, ou simetria bilateral é simetria em relação à reflexão.
É o tipo mais comum de simetria. Em 2D não é um eixo de simetria, em 3D de um plano de simetria. Um objeto ou figura que se confunde com a sua imagem transformada é chamado de espelho simétrico (ver imagem de espelho).
O eixo de simetria de uma figura bidimensional é uma linha de modo a que, se uma perpendicular é construída, quaisquer dois pontos que ficam na perpendicular a distâncias iguais do eixo de simetria são idênticos. Outra maneira de pensar sobre isso é que, se a forma fosse para ser dobrado ao meio sobre o eixo, as duas metades seria idêntico: as duas metades são imagem de espelho um do outro. Assim, um quadrado tem quatro eixos de simetria, porque há quatro maneiras diferentes para dobrá-lo e têm as bordas durante toda a partida. Um círculo tem infinitas eixos de simetria, pela mesma razão.
Se a letra T é reflectido ao longo de um eixo vertical, parece que a mesma. Note que este é às vezes chamado simetria horizontal e vertical, simetria, por vezes! Pode-se utilizar melhor uma formulação inequívoca, por exemplo, "T tem um eixo de simetria vertical."
Os triângulos são simetria com este isósceles , os quadriláteros com esta simetria são o pipas e os isósceles trapézios.
Para cada linha ou plano de reflexão, o grupo de simetria é isomorfo com Cs (veja grupos de pontos em três dimensões), um dos três tipos de ordem dois (Involuções), daí algebricamente C2. O domínio fundamental é um semi-plano ou semi-espaço.
Bilateria (bilaterais animais, incluindo os seres humanos) são mais ou menos simétrica em relação à plano sagital.
Em certos contextos, há simetria rotacional de qualquer maneira. Em seguida, espelho de imagem simetria é equivalente com inversão simetria; em tais contextos da física moderna, o termo P-simetria é usado para ambos (P significa paridade).
Para os tipos mais gerais de reflexão não são correspondentes tipos mais gerais de simetria de reflexão. Exemplos:
- com respeito a um não- isométrica afim involução (uma reflexão em uma linha oblíqua, avião, etc).
- em relação a círculo de inversão
Simetria rotacional
Ver simetria rotacional.
Simetria rotacional é simetria em relação a algumas ou todas as rotações em m-dimensional espaço euclidiano. Rotações são isometries diretos, ou seja, isometrias preservação orientação. Por conseguinte, um grupo de simetria de simetria de rotação é um subgrupo de E + (m) (ver Grupo euclidiana).
Simetria em relação a todas as rotações em torno de todos os pontos implica a simetria de translação em relação a todas as traduções, e o grupo de simetria é toda a E + (m). Isto não se aplica para os objetos porque torna espaço homogêneo, mas pode aplicar para leis físicas.
Por simetria em relação a rotações em torno de um ponto, podemos tomar esse ponto como origem. Estas rotações formar o grupo ortogonal especial SO (m), o grupo de m × m matrizes ortogonais com determinante 1. Para m = 3 este é o grupo de rotação.
Em outro sentido da palavra, o grupo de um objeto de rotação é o grupo de simetria dentro E + (n), o grupo de isometrias diretos; em outras palavras, a intersecção do grupo de simetria completa e o grupo de isometries directos. Para objectos quirais é o mesmo que o grupo de simetria completa.
Leis da física são SO (3) -invariant se eles não distinguem diferentes direções no espaço. Por causa de Teorema de Noether, a simetria de rotação de um sistema físico é equivalente à lei de conservação do momento angular. Veja também invariância rotacional.
Simetria translacional
Ver artigo principal simetria de translação.
Simetria translacional deixa uma invariante objeto em um grupo discreto ou contínuo de traduções 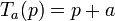
Glide simetria de reflexão
A deslize simetria de reflexão (em 3D: um plano de simetria deslize) significa que uma reflexão em uma linha ou plano combinado com uma translação ao longo da linha / no plano, resulta no mesmo objecto. Implica simetria translacional com o dobro do vetor de translação.
O grupo de simetria é isomorfo com Z.
Rotoreflection simetria
Em 3D, ou rotoreflection rotação indevido no sentido estrito é a rotação em torno de um eixo, combinada com reflexão num plano perpendicular a esse eixo. Como grupos de simetria em relação a um roto-reflexão, podemos distinguir:
- o ângulo não tem divisor comum com 360 °, o grupo de simetria não é discreto
- 2 vezes de n rotoreflection (ângulo de 180 ° / n) com grupo de simetria S 2n de ordem 2 n (não ser confundido com grupos simétricos, para que a mesma notação é usada; Resumo grupo C 2n); Um caso especial é n = 1, inversão, porque não dependem do eixo e o plano, que é caracterizada por apenas o ponto de inversão.
- C nh (ângulo de 360 ° / n); para impar n esta é gerada por uma única simetria, e o grupo C é 2n resumo, para ainda n esta não é uma simetria de base, mas uma combinação. Veja também grupos de pontos em três dimensões.
Simetria helicoidal

Simetria helicoidal é o tipo de simetria visto em tais objetos do cotidiano como molas, Brinquedos furtivos, brocas, e augers. Ele pode ser pensado como simetria de rotação juntamente com translação ao longo do eixo de rotação, o eixo parafuso). O conceito de simetria helicoidal pode ser visualizado como o rastreio em três dimensões do espaço, que resulta de rodar um objecto contra um mesmo velocidade angular, ao mesmo tempo movendo-se a outro, mesmo a velocidade ao longo do seu eixo de rotação (tradução). Em qualquer ponto no tempo, esses dois movimentos se combinam para dar um ângulo de enrolamento que ajuda a definir as propriedades do traçado. Quando o objeto traçar gira rapidamente e traduz-se lentamente, o ângulo de enrolamento estará próximo de 0 °. Por outro lado, se a rotação é lento e a tradução rápida, o ângulo de enrolamento vai se aproximar de 90 °.
Três classes principais de simetria helicoidal podem ser distinguidos com base na interação do ângulo de bobinamento e de tradução simetrias ao longo do eixo:
- Simetria helicoidal infinito. Se não existem características distintas ao longo do comprimento de um hélice ou hélice-como objeto, o objeto terá simetria infinita muito parecida com a de um círculo, mas com a exigência adicional de tradução ao longo do eixo do objeto de devolvê-lo à sua aparência original. Um objecto em hélice é aquele que tem em cada ponto o ângulo regulares de enrolamento de uma hélice, mas que também pode ter um secção transversal de alta complexidade indefinidamente, com a única condição existe precisamente a mesma secção transversal (normalmente depois de uma rotação) em todos os pontos ao longo do comprimento do objecto. Exemplos simples incluem uniformemente enrolada molas, slinkies, brocas, e augers. Indicar com maior precisão, um objeto tem simetrias helicoidais infinitas, se por qualquer pequena rotação do objeto em torno de seu eixo central existe um ponto próximo (a distância tradução) em que o eixo em que o objeto vai aparecer exatamente como fazia antes. É esta simetria helicoidal infinito que dá origem à ilusão curioso de movimento ao longo do comprimento de um parafuso sem fim ou parafuso de bit que está sendo girada. Ele também fornece a capacidade útil mecanicamente de tais dispositivos para mover materiais ao longo do seu comprimento, desde que eles são combinados com uma força como a gravidade ou fricção que permite que os materiais para resistir simplesmente rotativa, juntamente com a broca ou sem-fim.
- n vezes simetria helicoidal. Se o requisito de que cada secção transversal do objecto helicoidal ser idênticos é relaxado, simetrias helicoidais menores adicionais tornam-se possíveis. Por exemplo, a secção transversal do objecto helicoidal pode mudar, mas ainda se repete de uma forma regular ao longo do eixo do objecto helicoidal. Por conseguinte, objectos deste tipo irá apresentar uma simetria, após uma rotação de ângulo fixo por alguns
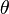 e uma tradução feita alguma distância fixa, mas não vai, em geral, ser invariante para qualquer ângulo de rotação. Se o ângulo (rotação) na qual a simetria ocorre uniformemente divide em uma volta completa (360 °), o resultado é o equivalente helicoidal de um polígono regular. Este processo é chamado de simetria helicoidal N vezes, onde N = 360 ° /
e uma tradução feita alguma distância fixa, mas não vai, em geral, ser invariante para qualquer ângulo de rotação. Se o ângulo (rotação) na qual a simetria ocorre uniformemente divide em uma volta completa (360 °), o resultado é o equivalente helicoidal de um polígono regular. Este processo é chamado de simetria helicoidal N vezes, onde N = 360 ° / 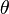 Ver, por exemplo dupla hélice. Este conceito pode ser mais generalizado para incluir os casos
Ver, por exemplo dupla hélice. Este conceito pode ser mais generalizado para incluir os casos 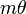 é um múltiplo de 360 °, isto é, o ciclo se repetir, eventualmente, mas apenas depois de mais do que uma rotação completa do objecto helicoidal.
é um múltiplo de 360 °, isto é, o ciclo se repetir, eventualmente, mas apenas depois de mais do que uma rotação completa do objecto helicoidal.
- Não-repetição simetria helicoidal. Este é o caso em que o ângulo de rotação
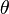 necessária para observar a simetria é um número irracional, tal como
necessária para observar a simetria é um número irracional, tal como 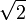 radianos que nunca se repete exatamente, não importa quantas vezes a hélice é rodado. Tais simetrias são criados usando um não-repetição ponto grupo em duas dimensões. ADN é um exemplo deste tipo de simetria helicoidal não-repetição.
radianos que nunca se repete exatamente, não importa quantas vezes a hélice é rodado. Tais simetrias são criados usando um não-repetição ponto grupo em duas dimensões. ADN é um exemplo deste tipo de simetria helicoidal não-repetição.
Simetria escala e fractais
Escala de simetria refere-se a ideia de que se um objecto é expandido ou reduzido em tamanho, o novo objecto tem as mesmas propriedades que o original. Escala simetria é notável pelo fato de que ele não existe para a maioria dos sistemas físicos, um ponto que foi discernida pela primeira vez por Galileo . Exemplos simples da falta de simetria escala em todo o mundo físico incluem a diferença na força e tamanho das pernas de elefantes contra ratinhos , e a observação de que, se uma vela de cera macia foi ampliado para o tamanho de uma árvore de altura, desmoronaria imediatamente sob seu próprio peso.
A forma mais sutil de simetria escala é demonstrado por fractais . Tal como concebido por Mandelbrot, fractais são um conceito matemático em que a estrutura de uma forma complexa parece exatamente o mesmo, não importa o grau de ampliação é usado para examiná-lo. A costa é um exemplo de um fractal que ocorre naturalmente, uma vez que retém aproximadamente comparável e de aparência semelhante em cada nível de complexidade do ponto de vista de um satélite para um exame microscópico de forma a água regaços-se contra os grãos de areia individuais. A ramificação das árvores, o que permite que as crianças a usar pequenos galhos como stand-ins para árvores cheias em dioramas, é outro exemplo.
Esta semelhança com fenômenos que ocorrem naturalmente fornece fractais com uma familiaridade cotidiana não tipicamente visto com funções matematicamente gerados. Como conseqüência, eles podem produzir resultados espantosamente belas, como o conjunto de Mandelbrot . Curiosamente, fractais também ter encontrado um lugar em CG, ou os efeitos de filmes gerados por computador, onde sua capacidade de criar as curvas muito complexas com simetrias fractais resultado em mais realista mundos virtuais.
Combinações de simetria
Ver combinações de simetria.
Simetria na ciência
Simetria na física
Simetria na física foi generalizado para dizer invariância, isto é, a falta de qualquer mudança visível sob qualquer tipo de transformação. Este conceito tornou-se uma das mais poderosas ferramentas de física teórica, como se tornou evidente que praticamente todas as leis da natureza são originários de simetrias. Na verdade, esse papel inspirou o Prêmio Nobel PW Anderson para escrever em seu amplamente ler artigo 1972 é mais diferente que "só é ligeiramente exagero dizer que a física é o estudo da simetria." Ver Teorema de Noether (que, como uma simplificação grosseira, indica que, para cada simetria matemática contínuo, existe uma quantidade conservada correspondente; uma corrente conservada, na língua de origem de Noether); e também, A classificação de Wigner, que diz que as simetrias das leis da física determinar as propriedades das partículas encontradas na natureza.
Simetria em objetos físicos
Objetos clássicos
Embora um objecto quotidiano pode aparecer exactamente o mesmo após uma operação de simetria, tais como uma rotação ou uma troca de duas partes idênticas foi realizada sobre ele, é facilmente evidente que uma tal simetria é verdadeiro apenas como uma aproximação para qualquer objecto físico normal.
Por exemplo, se uma roda de um alumínio precisamente usinado triângulo equilátero 120 graus em torno de seu centro, um observador casual trazido antes e depois da rotação será incapaz de decidir se quer ou não uma tal rotação ocorreu. No entanto, a realidade é que cada canto de um triângulo sempre aparece único quando examinado com suficiente precisão. Um observador armado com equipamento de medição suficientemente detalhadas, como óptico ou microscópios eletrônicos não será enganado; ele vai imediatamente reconhecer que o objeto tenha sido rodado, procurando por detalhes como cristais ou deformidades menores.
Essa simples experiências de pensamento mostrar que as afirmações de simetria em objetos físicos diários são sempre uma questão de semelhança aproximado em vez de mesmice de matemática precisa. A consequência mais importante desta natureza aproximada de simetrias em objetos físicos todos os dias é que essas simetrias têm impactos mínimos ou nenhum sobre a física de tais objetos. Por conseguinte, só o mais profundo simetrias de espaço e tempo desempenham um papel importante na física clássica, isto é, a física dos objetos grandes, todos os dias.
Objetos quânticos
Notavelmente, existe um reino da física para que afirmações matemáticas de simetrias simples em objetos reais deixam de ser aproximações. Que é o domínio da física quântica , que em sua maior parte é a física do muito pequeno, objetos muito simples, tais como elétrons , prótons , luz e átomos .
Ao contrário de objetos do cotidiano, objetos como elétrons têm número muito limitado de configurações, chamado estados, em que pode existir. Isto significa que, quando as operações de simetria, tais como trocando as posições dos componentes são aplicados a elas, as configurações resultantes novos muitas vezes não podem ser distinguidos dos originais não importa como um diligente observador está. Consequentemente, para suficientemente pequenas e simples objetos do genérico afirmação simetria matemática F (x) = x deixa de ser aproximada e, em vez torna-se uma descrição experimentalmente preciso e exato da situação no mundo real.
Consequências da simetria quântica
Enquanto faz sentido que simetrias poderia se tornar exata quando aplicada aos objetos muito simples, a intuição imediata é que tal detalhe não deve afetar a física de tais objetos de qualquer forma significativa. Isto é em parte porque é muito difícil de ler o conceito de semelhança exacta como fisicamente significativa. A nossa imagem mental de tais situações é invariavelmente o mesmo que usamos para objetos grandes: Nós retratar objetos ou configurações que são muito, muito semelhante, mas para as quais se poderia "olhar mais de perto" ainda seria capaz de dizer a diferença.
No entanto, a suposição de que simetrias exatas em objetos muito pequenos não deve fazer qualquer diferença em sua física foi descoberta no início de 1900 para ser espetacularmente errada. A situação foi sucintamente resumido por Richard Feynman nas transcrições diretas de sua Feynman Lectures on Physics, Volume III, Seção 3.4, partículas idênticas. (Infelizmente, a citação foi editado fora da versão impressa da mesma conferência.)
- "... Se houver uma situação física em que é impossível dizer que assim que aconteceu, ele sempre interfere, que nunca falha."
A palavra " interfere "neste contexto é uma maneira rápida de dizer que tais objetos são abrangidos pelas regras da mecânica quântica , em que eles se comportam mais como ondas que interferem do que como todos os dias objetos grandes.
Em suma, quando um objeto se torna tão simples que uma afirmação simetria da forma F (x) = x torna-se uma declaração exata da mesmice experimentalmente verificável, x deixa de seguir as regras da física clássica e devem ser modeladas utilizando as regras de intuitivo mais complexas-e muitas vezes muito menos de física quântica .
Essa transição também fornece uma informação importante sobre por que a matemática da simetria são tão profundamente entrelaçados com os de mecânica quântica. Quando os sistemas físicos fazer a transição de simetrias que são aproximados para aqueles que são exatas, as expressões matemáticas dessas simetrias deixará de ser aproximações e são transformados em definições precisas da natureza subjacente dos objetos. A partir desse ponto, a correlação de tais objetos para suas descrições matemáticas torna-se tão perto que é difícil separar os dois.
Symmetry como um princípio unificador da geometria
O geômetra alemão Felix Klein enunciou uma muito influente Programa de Erlangen, em 1872, sugerindo a simetria como unificador e organizar princípio da geometria (numa altura em que foi lido 'geometrias'). Esta é uma ampla em vez de princípio profunda. Inicialmente, conduziu ao interesse nos grupos ligados a geometrias, e a palavra de ordem geometria transformação (um aspecto da New Math, mas dificilmente controverso na prática matemática moderna). Até agora ele tem sido aplicado em diversas formas, como tipo de ataque padrão em problemas.
Simetria em matemática
Um exemplo de uma expressão matemática que exibe simetria é um ² c + 3 + ab b c ². Se a e b são trocadas, a expressão permanece inalterada devido ao commutativity de adição e multiplicação.
Como na geometria, para os termos existem duas possibilidades:
- ele próprio é simétrica
- que tem um ou mais outros termos simétricos com ele, de acordo com o tipo de simetria
Veja também função simétrica, dualidade (matemática)
Simetria na lógica
A relação diádica R é simétrica se e somente se, sempre que seja verdade que Rab, é verdade que Rba. Assim, "é a mesma idade que" é simétrica, pois se Paul é a mesma idade de Mary, Mary, em seguida, é a mesma idade de Paul.
Binário simétrico conectivos lógicos são " e "(∧, 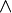 Ou &), " ou "(∨)," bicondicional "( sse) (↔), NAND ("não-e"), XOR ("não-bicondicional"), e NOR ("não-ou").
Ou &), " ou "(∨)," bicondicional "( sse) (↔), NAND ("não-e"), XOR ("não-bicondicional"), e NOR ("não-ou").
Generalizações de simetria
Se temos um dado conjunto de objetos com alguma estrutura, então é possível que uma simetria para converter meramente apenas um objeto em outro, em vez de agir sobre todos os objetos possíveis simultaneamente. Isto requer uma generalização do conceito de grupo de simetria ao de um grupóide.
Os físicos têm surgido com outras direcções de generalização, como supersimetria e grupos quânticos.
Simetria bilateral
Ver simetria (biologia) e simetria facial.
Simetria em Química
A simetria é importante para a química porque explica observações em espectroscopia , química quântica e cristalografia. Ele se baseia fortemente na teoria do grupo .
Simetria na história, religião e cultura
Em todo o esforço humano para que um resultado visual impressionante é parte do objetivo desejado, simetrias desempenhar um papel profundo. O apelo inato de simetria pode ser encontrada em nossas reações a acontecendo em toda objetos naturais altamente simétricas, tais como cristais precisamente formados ou conchas lindamente espiralados. Nossa primeira reação em encontrar tal objeto é muitas vezes a pensar se temos encontrado um objeto criado por um sujeito humano, seguido rapidamente por surpresa que as simetrias que me chamou a atenção derivam da própria natureza. Em ambas as reações nós damos a nossa inclinação para ver simetrias tanto como bonito e, de alguma forma, informativo do mundo que nos rodeia.
Simetria em símbolos religiosos
A tendência das pessoas para ver propósito na simetria sugere, pelo menos, uma razão pela qual simetrias são muitas vezes parte integrante dos símbolos das religiões do mundo. Apenas alguns dos muitos exemplos incluem o sêxtuplo simetria de rotação do judaísmo 's Estrela de David, a dupla apontar simetria do Taoísmo 's Taijitu ou Yin-Yang, o simetria bilateral do cristianismo 's atravessar e Sikhismo 's Khanda, ou a simetria quádrupla ponto de Versão antiga (e pacificamente a que se destina) de Jain da suástica . Com suas fortes proibições contra o uso de imagens representacionais, Islam , e em particular o Ramo sunita do Islã, desenvolveu alguns dos usos mais intrincado e visualmente impressionante de simetrias para usos decorativos de qualquer religião principal.
A antiga Imagem Taijitu do taoísmo é um uso particularmente fascinante de simetria em torno de um ponto central, combinado com inversão preto-e-branco da cor em distâncias opostas a partir desse ponto central. A imagem, que é muitas vezes incompreendido no Mundo ocidental como representando bom (branco) contra o mal (preto), é realmente pretende ser um representante gráfica da necessidade complementar para dois conceitos abstratos de "masculinidade" (branco) e "feminilidade" (preto). A simetria do símbolo, neste caso, é usado não apenas para criar um símbolo que chama a atenção do olho, mas para fazer uma declaração significativa sobre as crenças filosóficas das pessoas e grupos que a utilizam. Também um importante símbolo religioso simétrico é o xintoísta "Torii" "A porta das aves", geralmente à porta dos templos xintoístas chamados "Jinjas".
Simetria nas interações sociais
Pessoas observar a natureza simétrica, muitas vezes incluindo equilíbrio assimétrico, de interações sociais em uma variedade de contextos. Estes incluem avaliações de reciprocidade, empatia, desculpa, diálogo, respeito, justiça e vingança. Interações simétricas enviar a mensagem "somos todos iguais", enquanto interações assimétricas enviar a mensagem "Eu sou especial; melhor do que você". Relações entre pares são baseados em simetria, as relações de poder são baseadas em assimetria.
Simetria na arquitetura
Outra atividade humana em que o resultado visual desempenha um papel vital no resultado global é arquitetura . Tanto nos tempos antigos, a capacidade de uma grande estrutura para impressionar ou até mesmo intimidar seus telespectadores tem sido muitas vezes uma parte importante da sua finalidade, bem como a utilização de simetria é um aspecto inevitável de como realizar esses objetivos.
Apenas alguns exemplos de antigos exemplos de arquiteturas que fizeram uso poderoso de simetria para impressionar aqueles em torno deles incluiu a egípcia Pirâmides , o grego Parthenon , ea primeira e segunda Templo de Jerusalém, da China Cidade Proibida, Cambodia 's Angkor Wat complexo, e os muitos templos e pirâmides do antigo Civilizações pré-colombianas. Mais recentes exemplos históricos de arquiteturas enfatizando simetrias incluem Catedrais góticas, arquitetura e americana presidente Thomas Jefferson 's Monticello casa. India 's incomparável Taj Mahal está em uma categoria por si só, uma vez que pode ser indiscutivelmente um dos usos mais impressionantes e belas de simetria em arquitetura que o mundo já viu.

Um exemplo interessante de um quebra de simetria na arquitetura é a torre inclinada de Pisa , cuja notoriedade decorre em grande parte, não para a simetria pretendido de seu design, mas pela violação do que a simetria do lean que desenvolveu enquanto ele ainda estava em construção. Exemplos modernos de arquiteturas que fazem uso impressionante ou complexo de várias simetrias incluem Austrália 's surpreendente Sydney Opera House e Houston, Texas 's mais simples Astrodome.
Simetria encontra suas maneiras em arquitetura em todas as escalas, desde os pontos de vista globais externos, através da disposição do indivíduo planos de chão, e para baixo para o projeto de elementos de construção individuais, tais como portas intricada cedeu, vitrais , mosaicos , frisos, escadas, corrimões de escadas, e balustradess. Por pura complexidade e sofisticação na exploração de simetria como um elemento arquitectónico, islâmicos edifícios como o Taj Mahal, muitas vezes eclipse aqueles de outras culturas e idades, em parte devido à proibição geral do Islã contra o uso de imagens de pessoas ou animais.
Links relacionados à simetria na arquitetura incluem:
- Williams: Symmetry em Arquitetura
- Aslaksen: Matemática em Arte e Arquitetura
Simetria em vasos de cerâmica e metal

Desde os primeiros usos de rodas de cerâmica para ajudar vasos de barro forma, cerâmica teve uma forte relação de simetria. No mínimo, a cerâmica criada usando uma roda necessariamente começa com simetria rotacional integral na sua secção transversal, ao mesmo tempo permitindo a liberdade de forma substancial na direcção vertical. Após esta inerentemente simétricos culturas de ponto de partida desde os tempos antigos têm tendência para acrescentar outros padrões que tendem a explorar ou em muitos casos, reduzir a simetria rotacional completo original para um ponto onde alguns objectivo visual específica é conseguida. Por exemplo, persa cerâmica que datam do quarto milênio aC e usado anteriormente ziguezagues simétricas, praças, cruzamentos eclosões e repetições de números para produzir projetos globais mais complexas e visualmente impressionante.
Vasos de metal fundido faltava a simetria rotacional inerente feitos à roda de oleiro, mas caso contrário, proporcionou uma oportunidade semelhante para decorar suas superfícies com padrões agradáveis para aqueles que os usados. A antiga chinês, por exemplo, usou padrões simétricos em suas peças fundidas em bronze, logo no 17o vasos século BC Bronze exibiu tanto um motivo principal bilateral e um design fronteira traduzido repetitivo.
Links:
- Chinavoc: The Art of Bronzes chineses
- Grant: Cerâmica iraniana no Instituto Oriental
- O Metropolitan Museum of Art - Arte Islâmica
Simetria em colchas

Como mantas são feitos a partir de blocos quadrados (normalmente 9, 16, 25 ou peças para um bloco) com cada pedaço menor que geralmente consiste em triângulos de tecido, a embarcação se presta facilmente à aplicação de simetria.
Links:
- Quate: Explorando Geometria Através Quilts
Simetria em tapetes e carpetes

Uma longa tradição do uso de simetria em carpete e padrões do tapete se estende por uma variedade de culturas. Americana índios Navajo usado diagonais corajosas e motivos retangulares. Muitos tapetes orientais têm centros refletidas e beiras intrincados que traduzem um padrão. Não surpreendentemente, tapetes retangulares normalmente usam quadrilátero simetria, ou seja, motivos que se refletem em ambos os eixos horizontal e vertical.
Links:
- Mallet: Tapetes Orientais tribais
- Dilucchio: Navajo Tapetes
Simetria na música
Simetria é, naturalmente, não se restringe às artes visuais. O seu papel na história da música toca muitos aspectos da criação e percepção da música.
Forma musical
Simetria tem sido usado como um constrangimento formal, por muitos compositores, tais como a forma de arco (ABCBA) usado por Steve Reich, Béla Bartók, e James Tenney (ou inchar). Na música clássica, Bach usou os conceitos de simetria de permutação e invariância; ver (link externo "Fugue No. 21," pdf ou Shockwave).
Estruturas de pitch
Simetria é também uma consideração importante na formação de escalas e acordes, tradicional ou música tonal sendo constituídas por grupos não-simétricos de arremessos, tais como a escala diatônica ou o acorde maior. Escalas ou acordes simétricas, como a escala hexafônica, acorde aumentado ou diminuído acorde de sétima (diminuída-diminuída sétimo), são disse a direção falta ou uma sensação de movimento para a frente, são ambíguas quanto à tecla central ou tonal, e têm a menos específica funcionalidade diatônica. No entanto, compositores como Alban Berg, Bartók Béla, e George Perle ter usado eixos de simetria e / ou ciclos de intervalo de uma forma análoga à chaves ou não- tonais tonais centros.
Perle (1992) explica "CE, DF #, [e] Eb-G, são diferentes instâncias do mesmointervalo ... outro tipo de identidade. ..has a ver com eixos de simetria. CE pertence a uma família de díades simetricamente relacionadas como segue: "
| D | D # | E | F | F # | G | G # | ||||||
| D | C # | C | B | A # | A | G # |
Assim, além de ser parte da família intervalo de 4, CE é também uma parte da família soma-4 (com C igual a 0).
| + | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||
| 2 | 1 | 0 | 11 | 10 | 9 | 8 | |||||||
| 4 | 4 | 4 | 4 | 4 | 4 | 4 |
Ciclos de intervalo são simétricos e, portanto, não Diatónica. No entanto, um segmento de sete passo do C5 (o ciclo das quintas, que são enharmonic com o ciclo de quartos) irá produzir a maior escala diatônica. Tonais cíclicos progressões nas obras de compositores românticos, como Gustav Mahler e Richard Wagner formar uma ligação com as sucessões passo cíclico na música atonal de modernistas, como Bartók, Alexander Scriabin, Edgard Varèse, e da escola de Viena. Ao mesmo tempo, estas progressões sinalizar o final da tonalidade.
A primeira composição alargada de forma consistente com base em relações de passo simétrico foi, provavelmente, de Alban Berg Quartet , Op. 3 (1910). (Perle, 1990)
Equivalência
Linhas tom ouclasse campoconjuntos que sãoinvariantes sobretrógrada são horizontalmente simétricas, sobinversão na vertical. Veja também ritmo assimétrico.
Simetria em outras artes e ofícios

O conceito de simetria é aplicada ao design de objetos de todas as formas e tamanhos. Outros exemplos incluem beadwork,mobiliário,pinturas de areia,knotwork,máscaras,instrumentos musicais, e muitos outros empreendimentos.
Simetria em estética
A relação de simetria para a estética é complexo. Certos simetrias simples, e, em particular, simetria bilateral, parecem ser profundamente enraizada na percepção inerente por seres humanos da saúde provável ou adequação de outros seres vivos, como pode ser visto pela simples experiência de distorcer um lado da imagem de um atraente enfrentar e pedindo aos espectadores para avaliar a atratividade da imagem resultante. Consequentemente, essas simetrias que imitam biologia tendem a ter um apelo inato que por sua vez aciona uma poderosa tendência para criar artefatos com simetria similar. Um só precisa de imaginar a dificuldade em tentar comercializar um altamente assimétrico carro ou caminhão para compradores de automóveis gerais a compreender o poder de simetrias de inspiração biológica, tais como simetria bilateral.
Outro apelo mais sutil de simetria é o da simplicidade, que por sua vez tem uma implicação de segurança, e familiaridade. Um quarto altamente simétrico, por exemplo, é inevitavelmente também uma sala em que qualquer coisa fora do lugar ou potencialmente ameaçador pode ser identificado com facilidade e rapidez. Pessoas que tenham, por exemplo, cresceram em casas cheias de ângulos retos exatos e precisamente artefatos idênticos podem encontrar a sua primeira experiência em se hospedar em um quarto com não há ângulos retos exatos e não há artefatos exatamente idênticas para ser altamente inquietante. Simetria, portanto, pode ser uma fonte de conforto, não apenas como um indicador de saúde biológica, mas também de um ambiente seguro e bem compreendido.
Contrapondo-se a essa é a tendência para a simetria excessiva de ser percebido como chato ou desinteressante. Os seres humanos, em particular, têm um forte desejo de explorar novas oportunidades ou explorar novas possibilidades, e um grau excessivo de simetria pode transmitir uma falta de tais oportunidades.
Ainda outra possibilidade é que quando as simetrias se tornar muito complexos ou muito desafiador, a mente humana tem uma tendência a "afinar-los para fora" e percebê-los em mais uma moda: comoruído que transmite nenhuma informação útil.
Finalmente, percepções e valorização de simetrias também são dependentes de fundo cultural. O uso muito maior de simetrias geométricas complexas em muitos islâmicos culturas, por exemplo, torna mais provável que as pessoas de tais culturas irão apreciar tais formas de arte (ou, inversamente, a rebelar-se contra eles).
Como em muitos empreendimentos humanos, o resultado da confluência de muitos desses fatores é que o uso eficaz de simetria em arte e arquitetura é complexa, intuitivo e altamente dependente das habilidades dos indivíduos que devem tecem e combinar tais fatores dentro de seu próprio criativo trabalho. Juntamente com textura, cor, proporção, e outros factores, a simetria é um ingrediente poderoso em qualquer síntese; um só precisa examinar o Taj Mahal para poderoso papel que a simetria execuções na determinação do apelo estético de um objeto.
Alguns exemplos do uso mais explícita de simetrias em arte pode ser encontrada na arte notável deMC Escher, o design criativo do conceito matemático de umgrupo papel de parede, e os muitos aplicativos (tanto matemáticas e reais) deladrilhos.
Simetria em jogos e quebra-cabeças
- Veja também jogos simétrica.
- Vejasudoku.
Jogos de tabuleiro
- O Xadrez Colecção Symmetrical
Simetria na literatura
Ver palindrome.
Simetria moral
- Olho por olho
- Reciprocidade
- Regra De Ouro
- Empatia & Simpatia
- Equilíbrio reflexivo


