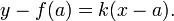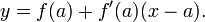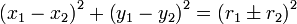Tangente

Assuntos Relacionados: Matemática

Fundo para as escolas Wikipédia

Esta seleção é feita para as escolas de caridade infantil leia mais . Patrocinar uma criança para fazer uma diferença real.

Tangente a uma curva.

Na geometria , a linha tangente (ou simplesmente a tangente) a uma curva num dado ponto é a linha reta que "apenas toca" a curva naquele ponto (no sentido explicado mais precisamente abaixo). À medida que passa através do ponto de tangência, a linha tangente está "indo na mesma direção", como a curva e, nesse sentido, é o melhor em linha reta aproximação à curva naquele ponto. A mesma definição aplica-se a curvas espaciais e curvas em n-dimensional espaço euclidiano .

De um modo semelhante, o plano tangente para uma superfície num determinado ponto é o plano que "apenas toca" a superfície nesse ponto. O conceito de uma tangente é uma das noções mais fundamentais em geometria diferencial e tem sido amplamente generalizada - ver Espaço tangente.

A palavra "tangente" vem do latim tangere, que significa "tocar".

A linha tangente a uma curva

Uma tangente, uma corda, e uma secante a um circulo.

A noção intuitiva de que uma tangente "apenas toca" uma curva pode ser mais explícita, considerando a sequência de linhas retas ( linhas secantes) que passam através de dois pontos, A e B, que se encontram na curva. A tangente em que A é o limite da progressão das linhas secantes como B move-se cada vez mais próximo de A. A existência e unicidade da linha tangente depende de um certo tipo de suavidade matemática, conhecido como "diferenciabilidade". Por exemplo, se dois arcos circulares encontram-se num ponto afiado (um vértice), então não há tangente exclusivamente definido no vértice porque o limite da progressão das linhas secantes depende da direcção na qual "ponto B" se aproxima do vértice.

Na maioria dos casos vulgarmente encontradas, a tangente a uma curva não atravessa a curva no ponto de tangência (embora possa, quando continuada, atravessar a curva em outros lugares longe do ponto de tangência). Isto é verdade, por exemplo, de todas as tangentes a um círculo ou um parábola. No entanto, nos pontos de chamada excepcionais pontos de inflexão, a linha tangente faz atravessar a curva no ponto de tangência. Um exemplo é o ponto (0,0) sobre o gráfico cúbico da parábola y = x ^3.

Por outro lado, pode acontecer que a curva está inteiramente de um lado de uma linha reta passando por um ponto sobre ele, e ainda esta linha reta não é uma linha tangente. Este é o caso, por exemplo, para uma linha que passa através do vértice de um triângulo e não interecting o triângulo - em que a linha tangente não existe, pelas razões explicadas anteriormente. Em geometria convexa, tais linhas são chamadas apoiar linhas.

Abordagem analítica

A ideia geométrico da linha tangente como o limite das linhas secantes serve como a motivação para métodos analíticos que são usados para encontrar linhas tangentes explicitamente. A questão de encontrar a linha tangente a um gráfico, ou o problema linha tangente, foi uma das questões centrais que levaram ao desenvolvimento de cálculo no século 17. No segundo livro da sua geometria René Descartes disse sobre o problema de construir a tangente a uma curva, "E eu ouso dizer que este não é apenas o problema mais útil e mais geral na geometria que eu sei, mas mesmo que eu já desejava saber."

Descrição intuitiva

Suponha-se que uma curva é dada como o gráfico de uma função , y = f (x). Para encontrar a linha tangente no ponto p = (a, f (a)), considerar um outro ponto q nas proximidades = (a + h, f (a + h)) na curva. O inclinação da A linha secante passando por p e q é igual ao diferença quociente

$\ Frac {f (a + h) -f (a)} {h}.$

À medida que o ponto Q se aproxima de p, o que corresponde a h tornando cada vez menor, o quociente de diferença deve aproximar-se de um certo valor limite K, que é a inclinação da linha tangente no ponto P. Se k é conhecido, a equação da linha tangente pode ser encontrado sob a forma de ponto de inclinação

$y-f (a) = K (X-a). \,$

Descrição mais rigorosa

Para fazer o raciocínio anterior rigorosa, é preciso explicar o que se entende pelo quociente diferença se aproxima de um determinado valor limite k. A formulação matemática precisa foi dada por Cauchy no século 19 e se baseia na noção de limite . Suponha que o gráfico não ter uma pausa ou uma borda afiada em p e não é nem prumo, nem muito perto wiggly p. Depois, há um valor único de k tal que quando h tende a 0, o quociente diferença fica cada vez mais perto de k, ea distância entre eles se torna insignificante em comparação com o tamanho do h, se h é pequeno o suficiente. Isto leva à definição da inclinação da linha tangente à curva como o limite dos quocientes diferença para a função f. Este limite é a derivada da função f em x = a, denotado f '(a). A utilização de derivados, a equação da reta tangente pode ser declarado como segue:

$y = f (a) + f '(a), (X-a). \,$

Cálculo fornece regras para calcular os derivados de funções que são dadas pelas fórmulas, como o função de potência, funções trigonométricas , função exponencial , logaritmo , e suas várias combinações. Assim, as equações de tangentes às gráficos de todas estas funções, assim como muitas outras, podem ser encontradas pelos métodos de cálculo.

Quando o método falha

Cálculo também demonstra que existem funções e os seus pontos de gráficos para os quais não existe o limite de determinação da inclinação da linha tangente. Para esses pontos a função f é não-diferenciável. Existem duas razões possíveis para o método de encontrar as tangentes, com base nos limites e derivados de falhar: ou a tangente geométrico existe, mas é uma linha vertical, que não pode ser dada sob a forma de ponto de inclinação, uma vez que não têm um inclinação, ou o gráfico é muito mal comportado de admitir uma tangente geométrica.

O gráfico y = x ^1/3 ilustra a primeira possibilidade: aqui o quociente diferença em a = 0 é igual a ^1/3 h / h = h ^{- 2/3,} que se torna muito grande quando h se aproxima de 0. A linha tangente esta curva na origem é vertical.

O gráfico y = | x | do valor absoluto função consiste em duas linhas retas com diferentes inclinações se juntou na origem. Como ponto q se aproxima da origem da direita, a linha secante sempre tem inclinação 1. Como ponto q se aproxima da origem a partir da esquerda, a linha secante sempre tem inclinação -1. Portanto, não há nenhuma tangente única para o gráfico na origem (embora, em certo sentido, existem duas meias-tangentes, correspondentes a duas orientações possíveis da abordagem da origem).

Círculos tangente.

Círculos tangente

Dois círculos , com raios de r _i e no centros (x _i, y _i), para i = 1, 2 são referidos como sendo tangentes entre si se

$\ Left (x_1 x_2-\ right) ^ 2 + \ left (y_1-y_2 \ right) ^ 2 = \ left (r_1 \ pm r_2 \ right) ^ 2$

Superfícies e manifolds de dimensão superior

O plano tangente a um superfície num dado ponto P é definido de uma forma análoga à linha tangente no caso de curvas. Ele é a melhor aproximação da superfície por um plano de p, e podem ser obtidos como a posição limite dos planos que passam através de três pontos distintos na superfície perto de p uma vez que estes pontos convirjam para p. De modo mais geral, existe uma -dimensional k espaço tangente em cada ponto de um k-dimensional colector no n -dimensional espaço euclidiano .

Retirado de " http://en.wikipedia.org/w/index.php?title=Tangent&oldid=205103638 "