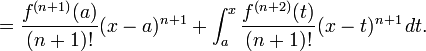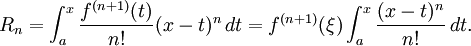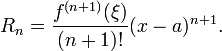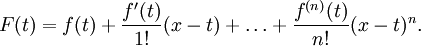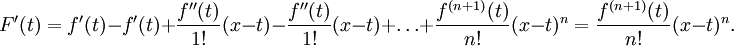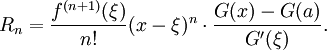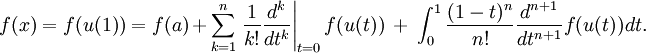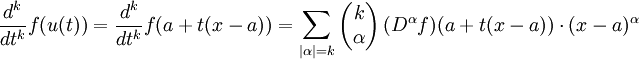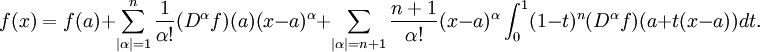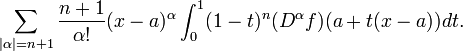Teorema de Taylor
Você sabia ...
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
No cálculo , o teorema de Taylor dá uma sequência de aproximações de um diferenciável função perto de um determinado ponto por polinômios (os polinômios Taylor dessa função) cujos coeficientes depende apenas dos derivados da função nesse ponto. O teorema também fornece estimativas precisas sobre o tamanho do erro na aproximação. O teorema é nomeado após o matemático Brook Taylor, que afirmou que em 1712, mesmo que o resultado foi descoberto 41 anos mais cedo em 1671 por James Gregory.
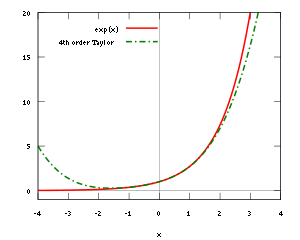
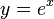 (Linha contínua vermelho) eo correspondente polinômio de Taylor de grau de quatro em torno da origem (linha verde tracejada).
(Linha contínua vermelho) eo correspondente polinômio de Taylor de grau de quatro em torno da origem (linha verde tracejada). Teorema de Taylor em uma variável
Um exemplo simples do teorema de Taylor é a aproximação da função exponencial 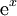 perto de x = 0:
perto de x = 0:
A indicação exacta do teorema é como se segue: Se n ≥ 0 é um número inteiro e F é uma função que é N vezes continuamente diferenciável no intervalo fechado [A, X] e N + 1 vezes diferenciável no intervalo aberto (a, x), então temos
Aqui, n! indica o fatorial de n, e R n (x) é um termo restante, que denota a diferença entre o polinómio de Taylor de grau n e a função original. O termo resto R n (x) depende de x e é pequeno, se x é perto o suficiente para um. Diversas expressões estão disponíveis para ele.
O Lagrange forma de resto o termo indica que existe um número ξ entre um e x tal que
Isso expõe o teorema de Taylor como uma generalização do teorema do valor médio. Na verdade, o teorema do valor médio é usado para provar o teorema de Taylor com o termo restante Lagrange.
O Forma de Cauchy do termo restante indica que existe um número ξ entre um e x tal que
De modo mais geral, se G (t) é uma função contínua em [A, X], que é diferenciável com derivado não-nulo em (a, x), então existe um número ξ entre um e x tal que
Isso expõe o teorema de Taylor como uma generalização do Cauchy teorema do valor médio.
O integrante formulário do termo restante é
desde que, como é frequentemente o caso, f (n) é absolutamente contínua em [a, x]. Isso mostra o teorema a ser uma generalização do teorema fundamental do cálculo .
Para algumas funções f (x), pode-se mostrar que o termo resto R n se aproxima de zero como n se aproxima do ∞; estas funções pode ser expressa como uma série de Taylor de uma vizinhança do ponto um e são chamados analítica.
O teorema de Taylor (com a formulação integral do termo restante) também é válido se a função f tem complexos ou valores vector valores. Além disso, existe uma versão do teorema de Taylor para funções de várias variáveis.
Para funções complexas analítica em uma região que contém um círculo em torno de um C e o seu interior, que tem um contorno expressão integral para o restante
dentro de C válida.
As estimativas do restante
Outra versão comum do teorema de Taylor mantém em um intervalo (a - r, a + r) onde a variável x é assumida a ter seus valores. Esta formulação do teorema tem a vantagem de que muitas vezes é possível controlar explicitamente o tamanho dos restantes termos, e, assim, chegar a uma aproximação de uma função válida em conjunto com um intervalo de limites precisos sobre a qualidade da aproximação.
A versão precisa do teorema de Taylor sob esta forma é a seguinte. Suponhamos que f é uma função que é N vezes continuamente diferenciável no intervalo fechado [A - R, A + R] e N + 1 vezes diferenciável no intervalo aberto (A - R, A + R). Se existe uma verdadeira constante Mn positivo tal que | f (n + 1) (x) | ≤ Mn para todo x ∈ (A - R, A + R), seguida
onde a função resto R n satisfaz a desigualdade (conhecida como estimativa de Cauchy):
para todo x ∈ (A - R, A + R). Isto é chamado um estimativa uniforme do erro no polinómio de Taylor, centrada num, porque mantém uniformemente para todos os x no intervalo.
Se, além disso, é f infinitamente diferenciável em [a - r, A + R] e
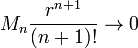 como
como 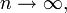
então f é analítica sobre (a - r, a + r). Em outras palavras, uma função analítica é a limite uniforme de sua polinômios Taylor em um intervalo. Isso faz com que a idéia de que preciso funções analíticas são aquelas que são iguais a sua série de Taylor.
Teorema de Taylor para diversas variáveis
O teorema de Taylor pode ser generalizada para várias variáveis como se segue. Seja B um bola em R N centrado em um ponto um, e f uma função real definida na encerramento 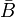 n ter um derivadas parciais contínuas em todos os pontos. Teorema de Taylor afirma que, para qualquer
n ter um derivadas parciais contínuas em todos os pontos. Teorema de Taylor afirma que, para qualquer 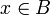 ,
,
onde a soma estende-se por multi-índices α (este usa a fórmula notação multi-índice).
Os termos restantes satisfazer a desigualdade
para todos α com | α | n = 1. Como foi o caso com uma variável, os termos restante pode ser descrita explicitamente. Veja a prova para obter detalhes.
Prova: o teorema de Taylor em uma variável
Versão Integral
Nós primeiro provar o teorema de Taylor com o prazo restante integral.
O teorema fundamental do cálculo afirma que
que pode ser rearranjada para:
Agora podemos ver que um pedido de Integração por partes rendimentos:
(A primeira equação é chegado por deixá 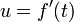 e
e 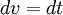 ; a segunda equação, observando que
; a segunda equação, observando que 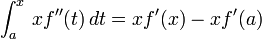 ; a terceira apenas fatores de alguns termos comuns.)
; a terceira apenas fatores de alguns termos comuns.)
Outro rendimentos de aplicação:
Repetindo esse processo, podemos derivar o teorema de Taylor para maiores valores de n.
Isso pode ser formalizado através da aplicação da técnica de indução. Então, suponha que o teorema de Taylor é válido para a n particular, isto é, suponha que
Podemos reescrever a integral usando integração por partes. Um anti derivada de (x - T) n como uma função de t é dado por - (x - T) n-1 / (n + 1), assim
Substituindo isso em (*) comprova o teorema de Taylor para n + 1, e, portanto, para todos os inteiros não negativos n.
O termo restante sob a forma de Lagrange pode ser derivada pela teorema do valor médio da seguinte forma:
A última integral pode ser resolvido imediatamente, o que leva a
Teorema do valor médio
Uma prova alternativa, que detém sob hipóteses técnicas mais suaves sobre a função f, pode ser fornecido usando o Cauchy teorema do valor médio. Seja G um função real contínua em [a, x] e diferenciável com derivado não de fuga em (a, x). Deixar
Por teorema do valor médio de Cauchy,
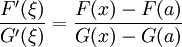 (1)
(1)
para alguns ∈ ξ (a, x). Note-se que o numerador de F (x) - F (a) R = n é o restante do Taylor polinomial para f (x). Por outro lado, a computação f (t),
Colocando esses dois fatos juntos e reorganizando os termos de rendimentos (1)
que era para ser mostrado.
Note-se que a forma de Lagrange o restante vem de tomar G (t) = (T - a), n 1, e dada a forma de Cauchy do restante vem de tomar G (t) = (T - a).
Prova: várias variáveis
Seja x = (x 1, ..., x N) encontram-se na esfera B com um centro. Parametrizar o segmento de linha entre um e x por u (t) = A + T (Xa). Nós aplicamos a versão de uma variável do teorema de Taylor para a função f (u (t)):
Pelo regra da cadeia para diversas variáveis,
onde  é o multinominal coeficiente para o α multi-índice. Desde
é o multinominal coeficiente para o α multi-índice. Desde 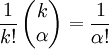 , Obtemos
, Obtemos
O termo restante é dada pela
Os termos deste somatório são formas explícitas para o α R na demonstração do teorema. Estes são facilmente visto para satisfazer a estimativa necessário.

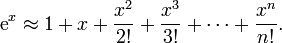
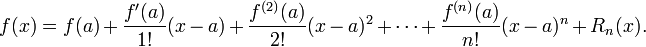
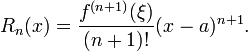
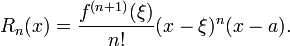
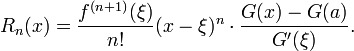
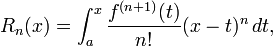
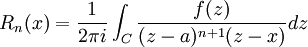
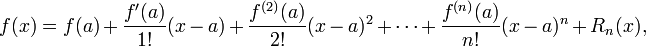
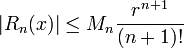
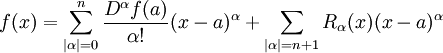
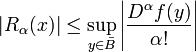
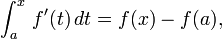
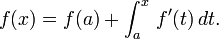
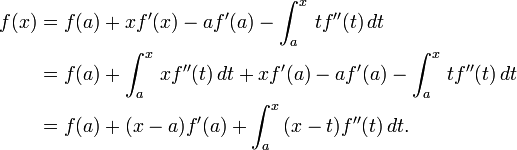
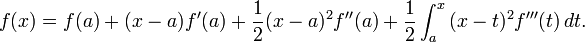
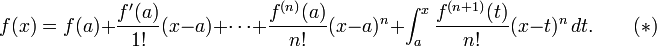
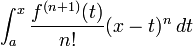
![{} = - \ Left [\ frac {f ^ {(n + 1)} (t)} {(n + 1) n!} (X - t) ^ {n + 1} \ right] _a ^ x + \ int_a ^ x \ frac {f ^ {(n + 2)} (t)} {(n + 1) n!} (x - t) ^ {n + 1} \, dt](../../images/127/12701.png)