
Volume
Você sabia ...
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Visite o site da SOS Children at http://www.soschildren.org/
O volume de qualquer sólido, líquido, ou gás é quanto três dimensional do espaço que ocupa, muitas vezes quantificados numericamente. Figuras unidimensionais (tais como linhas ) e formas bidimensionais (por exemplo, quadrados ) são atribuídos volume zero no espaço tridimensional.
Volumes de formas com bordas retas e circulares são calculados usando fórmulas aritméticas. Volumes de outras formas curvas são calculadas usando cálculo integral , através da aproximação do corpo dado com uma grande quantidade de pequenos cubos ou concêntrica cascas cilíndricas, e adicionando os volumes individuais dessas formas. O volume de objectos de forma irregular pode ser determinada pela deslocamento. Se um objeto de forma irregular é menos denso do que o líquido, você vai precisar de um peso para anexar ao objeto flutuante. Um peso suficiente fará com que o objeto a afundar. O volume final do objecto desconhecido pode ser encontrado através da subtracção do volume do objecto pesado em anexo e o volume total de fluido deslocado.
A generalização do volume para arbitrariamente muitas dimensões é chamado conteúdo. Na geometria diferencial , o volume é expressa por meio do forma de volume.
Volume e capacidade são, por vezes distinto, com capacidade de ser utilizado para o quanto um recipiente pode conter (com conteúdos medidos comumente em litros ou suas unidades de derivados) e de volume sendo a quantidade de espaço desloca um objeto (geralmente medido em metros cúbicos ou suas unidades de derivados). O volume de um gás disperso, é a capacidade do seu recipiente. Se mais de gás é adicionada a um recipiente fechado, o recipiente, quer se expande (como em um balão) ou o pressão no interior do recipiente aumenta.
Volume e capacidade são também distinguidos em um ambiente de gerenciamento de capacidade, onde a capacidade é definida como o volume durante um período de tempo especificado.
O volume é um parâmetro fundamental para a termodinâmica e é conjugado pressão.
| Variáveis conjugadas da termodinâmica | |
|---|---|
| Pressão | Volume |
| ( Estresse) | ( Strain) |
| Temperatura | Entropy |
| Potencial químico | Número de partículas |
Desconto fórmulas
| Comuns equações para o volume: | ||
|---|---|---|
| Forma | Equação | Variáveis |
| Um cubo : | 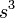 | s = comprimento de qualquer lado |
| Um rectangular prisma: | 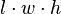 | l = l ength, w = w idth, h = h oito |
| A cilindro (prisma circular): | 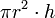 | r = raio de face circular, h = altura |
| Qualquer prisma que tem uma área de secção transversal constante ao longo da altura **: | 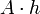 | A = área da base, h = altura |
| A esfera : | 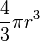 | r = raio da esfera que é o integrante do Área de superfície de uma esfera |
| Um elipsóide: | 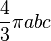 | a, b, c = semi-eixos de elipsóide |
| A pirâmide: | 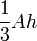 |
A = área da base, h = altura da pirâmide |
| A cone (pirâmide circular como base): | 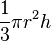 | r = raio do círculo na base, h = distância da base à ponta |
| Qualquer figura ( cálculo exigido) | 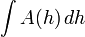 | h = qualquer dimensão da figura, A (h) = área das secções transversais perpendiculares ao h descrita como uma função da posição ao longo h. Isto irá funcionar para qualquer figura, se a sua área transversal pode ser determinado a partir h (não importa se o prisma é inclinada ou as secções transversais mudar de forma). ^ * |
(As unidades de volume depende das unidades de comprimento - se os comprimentos são, em metros, o volume será em metros cúbicos, etc.)
O volume de um paralelepípedo é o valor absoluto do produto escalar triplo dos vectores subtendem, ou equivalente, o valor absoluto do determinante da matriz correspondente.
O volume de qualquer tetraedro , dado seus vértices a, b, c e d, é (1/6) · | det (a - b, b - c, c - d) |, ou qualquer outra combinação de pares de vértices que formar um simplesmente conexa grafo.
Medidas de volume: Reino Unido
O Reino Unido está passando metrication e está usando cada vez mais o Unidades do sistema métrico SI de volume, ou seja, metro cúbico e litro. No entanto, alguns ex-unidades de volume ainda estão em diferentes graus de uso:
Imperial de volume de:
- Fluido Reino Unido onça, cerca de 28,4 ml (esta é igual ao volume de um avoirdupois onça de água sob certas condições)
- Reino Unido pint = 20 onças fluidas, ou cerca de 568 mL
- Reino Unido quart = 40 onças ou dois pints1.137 L
- Reino Unido galão = 4 quart, ou exatamente 4.546 09 L
O quart agora está obsoleta eo fl oz extremamente raros. O galão é utilizado apenas para fins de transporte, (que é ilegal para a gasolina e diesel a ser vendido pelo galão). A cerveja é a única unidade imperial que está em uso todos os dias, para a venda de cerveja e cidra (engarrafada e cerveja em lata é vendida principalmente em unidades SI) e para o leite (isso também é cada vez mais sendo vendido em unidades SI, principalmente Litros) .
Medidas de volume: cozinhar
Medidas tradicionais de cozinha para o volume também incluem:
- colher de chá = 1/6 US onças fluidas (cerca de 4,929 mL)
- colher de chá = 1/6 onças fluidas Imperial (cerca de 4.736 ml)
- colher de chá = 5 mL (métrico)
- colher de sopa = ½ US onças fluidas ou 3 colheres de chá (cerca de 14,79 mL)
- colher de sopa = ½ fluidas imperial onça ou 3 colheres de chá (cerca de 14,21 mL)
- colher de sopa = 15 mL ou 3 colheres de chá (métricas)
- colher de sopa = 5 fluidrams (cerca de 17,76 mL) (British)
- xícara = 8 US onças fluidas ou ½ US pinta líquido (cerca de 237 mL)
- xícara = 8 onças fluidas imperiais ou ½ litro de líquidos (cerca de 227 mL)
- copo = 250 mL (métrico)
Relação com a densidade
A densidade de um objecto é definida como a massa por unidade de volume.
O termo volume específico é utilizado para o volume dividido pela massa. Isto é o recíproco da densidade de massa , expressa em unidades tais como metros cúbicos por quilograma (metros cúbicos · kg -1).
Fórmula de derivação de volume
| Forma | Fórmula de derivação de volume |
|---|---|
| Esfera | O volume de uma esfera é o integrante de lajes circulares infinitesimais de largura 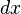 . . O cálculo do volume de uma esfera com centro de 0 e raio r é como se segue.
|

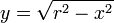
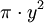
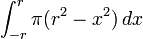
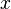 por
por 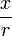 , De modo que os limites integrais tornar -1 e +1, obtemos
, De modo que os limites integrais tornar -1 e +1, obtemos 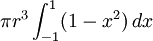
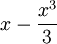
![\ Pi r ^ 3 \ cdot [1-1 / 3 - (- 1 + 1/3)]](../../images/206/20619.png) =
= 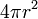 . O volume da esfera consiste em camadas de placas esféricas infinitesimais, e o volume é igual a esfera
. O volume da esfera consiste em camadas de placas esféricas infinitesimais, e o volume é igual a esfera 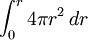 =
= 