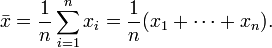Media aritmética

En matemáticas y estadísticas , la aritmética media (o simplemente la media) de una lista de números es la suma de todos los miembros de la lista, dividido por el número de elementos de la lista. Si la lista es un población estadística, a continuación, la media de la población que se llama una media de la población. Si la lista es una muestra estadística , llamamos a la resultante estadística de una media muestral.

La media es el tipo más comúnmente utilizado de promedio y se refiere a menudo simplemente como la media. El término "significa" o "media aritmética" es el preferido en las matemáticas y estadísticas para distinguirla de la otra promedios tales como la mediana y la de modo.

Introducción

Si denotamos un conjunto de datos por X = (x _1, x _2, ..., x _n), entonces el medio de muestra es típicamente denota con una barra horizontal sobre la variable ( 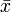, Enunciado "x bar").

El símbolo μ (griego: mu) se utiliza para denotar la media aritmética de toda una población. O, para una número aleatorio que ha definido una media, μ es la media probabilístico o valor esperado del número aleatorio. Si el conjunto X es una colección de números aleatorios con media probabilística de μ, a continuación, para cualquier muestra individual, x _i, a partir de esa colección, μ = E {x _i} es el valor esperado de esa muestra.

En la práctica, la diferencia entre μ y 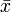es que μ es típicamente inobservable porque se observa sólo una muestra más que toda la población, y si la muestra se extrae al azar, entonces uno puede tratar 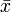, Pero no μ, como una variable aleatoria , la atribución de una distribución de probabilidad a la misma (la distribución muestral de la media).

Ambos se calculan de la misma manera:

Si X es una variable aleatoria , entonces la valor esperado de X puede ser visto como el largo plazo media aritmética que se produce en las mediciones repetidas de X. Este es el contenido de la ley de los grandes números. Como resultado, la media de la muestra se utiliza para estimar valores esperados desconocidos.

Tenga en cuenta que varios otros "medios" han sido definidos, incluyendo la Media generalizada, la f-media generalizada, la media armónica, la aritmético-geométrica media, y varios medios ponderados.

Ejemplos

• Si usted tiene 3 números después añadirlas y dividirlos por 3:
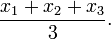
• Ellos y dividir Si tiene 4 números por añadir 4:

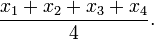
Problemas con algunos usos de la media

Mientras que la media se utiliza a menudo para informar tendencia central, puede que no sea apropiado para describir distribuciones asimétricas, ya que es fácilmente malinterpretados. La media aritmética está fuertemente influenciado por valores atípicos. Estas distorsiones pueden ocurrir cuando la media es diferente de la mediana. Cuando esto sucede, la mediana puede ser una mejor descripción de tendencia central.

Un ejemplo clásico es ingreso promedio. La media aritmética puede ser mal interpretado dar a entender que los ingresos de la mayoría de las personas son más altos que en realidad es el caso. Cuando se presentan con un uno "promedio" puede ser llevado a creer que los ingresos de la mayoría de la gente son cerca de este número. Este (media aritmética) de ingresos "promedio" es mayor que los ingresos de la mayoría de la gente, porque los valores extremos altos ingresos sesgar el resultado más alto (en contraste, el ingreso medio "resiste" tal inclinación). Sin embargo, este "promedio" no dice nada sobre el número de personas cerca de la renta mediana (ni tampoco dice nada sobre el ingreso modal que la mayoría de la gente está cerca). Sin embargo, debido a que se podría relacionar con descuido "promedio" y "la mayoría de la gente", uno de forma incorrecta podría suponer que los ingresos de la mayoría de la gente serían más altos (más cerca de esta inflada "promedio") de lo que son. Por ejemplo, informar de la "media" patrimonio neto en Medina, Washington como la media aritmética de todos los valores netos anuales producirían un número sorprendentemente alto debido a Bill Gates . Considere las puntuaciones (1, 2, 2, 2, 3, 9). La media aritmética es de 3.17, pero cinco de los seis valores están por debajo de este.

En ciertas situaciones, la media aritmética es la medida de la tendencia central mal del todo. Por ejemplo, si una acción cayó 10% en el primer año, y aumentó un 30% en el segundo año, entonces sería incorrecto reportar su incremento "promedio" por año durante este período de dos años como la media aritmética (-10% + 30%) / 2 = 10%; la media correcta en este caso es la media geométrica que produce un incremento promedio anual de sólo 8,2%. La razón para esto es que cada uno de esos porcentajes tienen diferentes puntos de partida. Si la acción comienza en $ 30 y cae 10%, ahora está en $ 27. Si la acción se eleva al 30%, es ahora de $ 35.1. La media aritmética de estas subidas es de 10%, pero dado que la acción subió por 5,1 dólares en 2 años, un promedio de 8,2% resultaría en la final de $ 35,1 figura [$ 30 (10.1%) (1 + 30%) = $ 30 (1 + 8,2%) (1 + 8,2%) = $ 35.1]. Si uno utilizó la media aritmética del 10% de la misma manera, uno no conseguir el aumento real [$ 30 (1 + 10%) (1 + 10%) = $ 36.3].

Debe tenerse especial cuidado cuando se utilicen los datos cíclicos tales como fases o ángulos. Tomando la media aritmética de 1 grado y 359 grados se obtiene un resultado de 180 grados, mientras que 1 y 359 son ambos adyacente a 360 grados, que puede ser un valor promedio más correcto. En aplicación general tal descuido conducirá al valor promedio móvil de forma artificial hacia el centro del rango numérico. Una solución a este problema es usar la formulación de optimización, y redefinir la diferencia como una distancia modular.