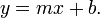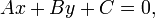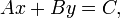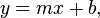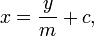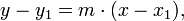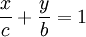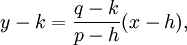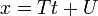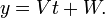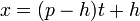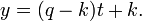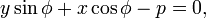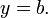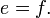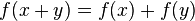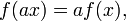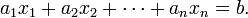Ecuación lineal
Antecedentes
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

Una ecuación lineal es una ecuación algebraica en la que cada plazo es o bien una constante o el producto de una constante por la primera potencia de una variable. Tal ecuación es equivalente a igualar una polinomio de primer grado a cero. Estas ecuaciones se llaman "lineal" porque representan líneas rectas en coordenadas cartesianas . Una forma común de una ecuación lineal en las dos variables 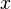 y
y 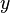 es
es
De esta forma, la constante 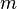 determinará el pendiente o gradiente de la línea; y la término constante
determinará el pendiente o gradiente de la línea; y la término constante 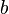 determinará el punto en el que la línea cruza el eje y. Ecuaciones con términos tales como x ², y un tercio, y xy se no lineal.
determinará el punto en el que la línea cruza el eje y. Ecuaciones con términos tales como x ², y un tercio, y xy se no lineal.
Los formularios para las ecuaciones lineales en 2D
Ecuaciones lineales complicadas, como las anteriores, pueden reescribirse usando las leyes de álgebra elemental en varias formas más simples. En lo que sigue x, y, t son variables; otras letras representan constantes (no especificadas pero los números fijos).
Forma general
- donde A y B no son ambos iguales a cero. La ecuación se escribe generalmente de modo que A ≥ 0, por convención. El gráfico de la ecuación es una línea recta , y cada línea recta puede ser representado por una ecuación en la forma anteriormente. Si A es distinto de cero, entonces la interceptación x, que es la x - de coordenadas del punto donde la gráfica cruza el eje x (y es cero), es - C / A. Si B es distinto de cero, entonces la interceptación y, que es la coordenada y del punto donde la gráfica cruza el eje y (x es cero), es - C / B, y el pendiente de la línea es - A / B.
Forma estándar
- donde A, B, y C son números enteros cuyos máximo común divisor es 1, A y B no son ambos igual a cero y, A es no negativo (y si A = 0 entonces B tiene que ser positivo). La forma estándar se puede convertir a la forma general, pero no siempre a todas las otras formas si A o B es cero.
Forma pendiente-intersección
Y-eje fórmula
- donde m es la pendiente de la línea y b es la interceptación, que es la coordenada y del punto donde la línea cruza el eje y. Esto puede ser visto por dejar
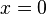 , Lo que da inmediatamente
, Lo que da inmediatamente 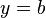 .
.
Fórmula eje X
- donde m es la pendiente de la línea y c es la interceptación x, que es la coordenada x del punto donde la línea cruza el eje x. Esto puede ser visto por dejar
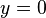 , Lo que da inmediatamente
, Lo que da inmediatamente  .
.
Forma punto-pendiente
- donde m es la pendiente de la línea y (x 1, y 1) es cualquier punto en la línea. Las formas de punto-pendiente y pendiente y de ordenadas son fácilmente intercambiables.
- La forma punto-pendiente expresa el hecho de que la diferencia en la coordenada y entre dos puntos en una línea (es decir,
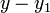 ) Es proporcional a la diferencia en la coordenada x (es decir,
) Es proporcional a la diferencia en la coordenada x (es decir, 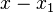 ). La constante de proporcionalidad es m (la pendiente de la línea).
). La constante de proporcionalidad es m (la pendiente de la línea).
Forma Intercepción
- donde c y b deben ser distinto de cero. La gráfica de la ecuación tiene x interceptación c ey interceptación b. La forma de intersección y se puede convertir en la forma estándar mediante el establecimiento de A = 1 / c, B = 1 / B y C = 1.
Forma de dos puntos
- donde p ≠ h. La gráfica pasa por los puntos (h, k) y (p, q), y tiene pendiente m = (q - k) / (p - h).
Forma paramétrica
- y
- Dos ecuaciones simultáneas en términos de un parámetro variable t, con pendiente m = V / T, x interceptación (VU - WT) / V e y interceptación (WT - VU) / T.
- Esto también puede estar relacionado con la forma de dos puntos, donde T = P - H, U = H, V = q - k, y W = k:
- y
- En este caso t varía de 0 en el punto (h, k) a 1 en el punto (p, q), con valores de t entre 0 y 1 que proporciona la interpolación y otros valores de t proporcionar extrapolación.
Forma normal
- donde φ es el ángulo de inclinación de la normal y p es la longitud de la normal. La normalidad se define como el segmento más corto entre la línea de que se trate y el origen. Forma normal se puede derivar de forma general dividiendo todos los coeficientes por
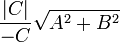 . Esta forma también llamado Hesse forma estándar, el nombre de un matemático alemán Ludwig Otto Hesse.
. Esta forma también llamado Hesse forma estándar, el nombre de un matemático alemán Ludwig Otto Hesse.
Casos especiales
- Este es un caso especial de la forma estándar en la que A = 0 y B = 1, o de la forma pendiente-intersección donde la pendiente M = 0. La gráfica es una línea horizontal con y interceptación igual a b. No hay x interceptación, a menos que b = 0, en cuyo caso la gráfica de la línea es el eje x, y así todo número real x es un interceptación.
- Este es un caso especial de la forma estándar en la que A = 1 y B = 0. La gráfica es una línea vertical con x interceptación igual a c. La pendiente no está definida. No hay interceptación y, a menos que c = 0, en cuyo caso la gráfica de la línea es el eje y, y por lo que cada número real y es un interceptación.
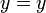 y
y 
- En este caso todas las variables y constantes han cancelado, dejando a un trivialmente verdadera declaración. La ecuación original, por lo tanto, sería llamado una identidad y que normalmente no considerarían su gráfica (que sería todo el plano xy xy). Un ejemplo es 2 x 4 + y = 2 (x + 2 y). Las dos expresiones a ambos lados del signo igual son siempre iguales, sin importar lo que los valores se utilizan para x e y.
- En situaciones donde la manipulación algebraica lleva a una afirmación como 1 = 0, entonces la ecuación original se llama inconsistente, lo que significa que no es cierto para cualquier valor de x e y (es decir, su gráfica sería la vacío set) Un ejemplo sería 3 x + 2 = 3 x - 5.
Conexión con funciones lineales y operadores
En todas las formas arriba mencionadas (suponiendo que el gráfico no es una línea vertical), la variable y es una función de x, y el gráfico de esta función es la gráfica de la ecuación.
En el caso particular de que la línea pasa por el origen, si la ecuación lineal se escribe en la forma y = f (x), entonces f tiene las propiedades:
y
donde A es cualquier escalar. Una función que satisface estas propiedades se llama una función lineal, o más generalmente una mapa lineal. Esta propiedad hace que las ecuaciones lineales particularmente fácil de resolver y razonar sobre.
Ecuaciones lineales se producen con gran regularidad en las matemáticas aplicadas . Mientras que surjan de forma natural al modelar muchos fenómenos, que son particularmente útiles, ya que muchos ecuaciones no lineales se pueden reducir a ecuaciones lineales suponiendo que las cantidades de interés varían a sólo una pequeña medida, de algún estado "fondo".
Ecuaciones lineales con más de dos variables
Una ecuación lineal puede implicar más de dos variables. La ecuación lineal general en n variables es:
De esta forma, a 1, a 2, ..., a n son los coeficientes, x 1, x 2, ..., x n son las variables, y b es la constante. Cuando se trata de tres o menos variables, es común para reemplazar x 1 con sólo x, x 2 con y, y z x 3 con, según el caso.
Tal ecuación representará una (n -1) -dimensional hiperplano en n-dimensional espacio euclidiano (por ejemplo, un plano en el 3-espacio).