
Volumen
Sabías ...
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/
El volumen de cualquier sólido, líquido, o gas es la cantidad de tres espacio tridimensional que ocupa, a menudo cuantificó numéricamente. Figuras unidimensionales (tales como líneas ) y formas de dos dimensiones (como cuadrados ) se asignan volumen cero en el espacio tridimensional.
Los volúmenes de formas de bordes rectos y circulares se calculan utilizando fórmulas aritméticas. Los volúmenes de otras formas curvas se calculan utilizando el cálculo integral , mediante la aproximación del cuerpo dada con una gran cantidad de pequeños cubos o concéntrica conchas cilíndricos, y la adición de los volúmenes individuales de esas formas. El volumen de objetos de forma irregular puede ser determinada por desplazamiento. Si un objeto de forma irregular es menos denso que el líquido, tendrá un peso para insertarse en el objeto flotante. Un peso suficiente hará que el objeto se hunda. El volumen final del objeto desconocido se puede encontrar restando el volumen del objeto pesado adjunto y el volumen total de fluido desplazado.
La generalización de volumen a arbitrariamente muchas dimensiones se llama contenido. En la geometría diferencial , el volumen se expresa por medio de la forma volumen.
Volumen y capacidad a veces se distinguen, con capacidad de ser utilizado por cuánto puede contener un recipiente (con contenidos medidos comúnmente en litros o sus unidades derivadas), y el volumen es la cantidad de espacio un objeto se desplaza (comúnmente miden en metros cúbicos o sus unidades derivadas). El volumen de un gas dispersado es la capacidad de su contenedor. Si más gas se añade a un recipiente cerrado, el recipiente o bien se expande (como en un globo) o la presión dentro de los aumentos de contenedores.
El volumen y la capacidad también se distinguen en un entorno de gestión de capacidad, donde la capacidad se define como el volumen durante un período de tiempo especificado.
El volumen es un parámetro fundamental en la termodinámica y es conjugado presión.
| Variables conjugadas de la termodinámica | |
|---|---|
| Presión | Volumen |
| ( Estrés) | ( Strain) |
| Temperatura | Entropía |
| El potencial químico | Número de la partícula |
Fórmulas Volumen
| Comunes ecuaciones para el volumen: | ||
|---|---|---|
| Forma | Ecuación | Variables |
| Un cubo : | 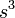 | s = longitud de cualquier lado |
| A rectangular prisma: | 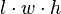 | l = l ength, w = w IDþ, h = h ocho |
| La cilindro (prisma circular): | 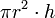 | r = radio de la cara circular, h = altura |
| Cualquier prisma que tiene un área de sección transversal constante a lo largo de la altura **: | 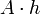 | A = área de la base, h = altura |
| Una esfera : | 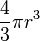 | r = radio de la esfera que es la integral de la Área de la superficie de una esfera |
| Una elipsoide: | 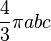 | a, b, c = semiejes de elipsoide |
| La pirámide: | 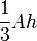 |
A = área de la base, h = altura de la pirámide |
| La cono (circular basado en pirámide): | 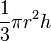 | r = radio del círculo en la base, h = distancia desde la base hasta la punta |
| Cualquier cifra ( cálculo requiere) | 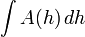 | h = cualquier dimensión de la figura, A (h) = área de las secciones transversales perpendiculares a h descrito como una función de la posición a lo largo h. Esto funcionará para cualquier figura si su área de sección transversal puede determinarse a partir h (no importa si el prisma es inclinada o las secciones transversales cambiar de forma). ^ * |
(Las unidades de volumen dependen de las unidades de longitud - si las longitudes son en metros, el volumen será en metros cúbicos, etc)
El volumen de una paralelepípedo es el valor absoluto de la triple producto escalar de los vectores que subtienden, o equivalentemente el valor absoluto de la determinante de la matriz correspondiente.
El volumen de cualquier tetraedro , dado sus vértices a, b, c y d, es (1/6) · | det (a - b, b - c, c - d) |, o cualquier otra combinación de pares de vértices que formar una simplemente conexo gráfico.
Las mediciones de volumen: Reino Unido
El Reino Unido está experimentando métrico y está utilizando cada vez más la Unidades del SI del sistema métrico de volumen, es decir, metro cúbico y litros. Sin embargo, algunas antiguas unidades de volumen se encuentran todavía en diversos grados de uso:
Unidades imperiales de volumen:
- Fluido Reino Unido oz, alrededor de 28,4 ml (esto es igual al volumen de una onza peso de agua bajo ciertas condiciones)
- Reino Unido pinta = 20 fl oz, o alrededor de 568 ml
- Reino Unido cuarto = 40 onzas o dos pints1.137 L
- Reino Unido galón = 4 cuartos, o exactamente 4,546 09 L
El cuarto ha quedado obsoleta y la onza de líquido extremadamente raro. El galón sólo se utiliza para usos de transporte, (que es ilegal para la gasolina y el diesel que se vende por galones). La pinta es la única unidad Imperial que se encuentra en el uso diario, para la venta de cerveza y la sidra (embotellado y cerveza en lata se vende principalmente en unidades del SI) y la leche (esto también es cada vez más se vende en unidades del SI, principalmente Litros) .
Las mediciones de volumen: cocinar
Medidas tradicionales de cocina para el volumen también se incluyen:
- = 1/6 cucharadita de US onza de líquido (aproximadamente 4.929 ml)
- cucharadita = 1/6 onza de líquido Imperial (aproximadamente 4.736 ml)
- cucharadita = 5 ml (métrico)
- = ½ cucharada de US onza líquida o 3 cucharaditas (unos 14,79 ml)
- = ½ cucharada de líquido Imperial onzas o 3 cucharaditas (unos 14,21 ml)
- cucharada = 15 ml o 3 cucharaditas (métricas)
- cucharada = 5 fluidrams (alrededor de 17,76 ml) (British)
- taza = 8 onzas líquidas de EE.UU. o ½ EE.UU. pinta líquido (aproximadamente 237 ml)
- taza = 8 onzas de líquido Imperial o ½ litro de líquido (aproximadamente 227 ml)
- taza = 250 ml (métrico)
Relación con la densidad
La densidad de un objeto se define como masa por unidad de volumen.
El término volumen específico se utiliza para el volumen dividido por la masa. Este es el recíproco de la densidad de masa , expresada en unidades tales como metros cúbicos por kilogramo (m³ · kg -1).
Volumen fórmula derivación
| Forma | Volumen fórmula derivación |
|---|---|
| Esfera | El volumen de una esfera es la integral de las losas circulares infinitesimales de ancho 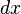 . . El cálculo para el volumen de una esfera con el centro 0 y el radio r es la siguiente.
|

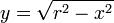
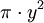
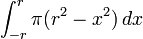
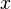 por
por 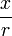 , De modo que los extremos de la integral se convierten en -1 y 1, obtenemos
, De modo que los extremos de la integral se convierten en -1 y 1, obtenemos 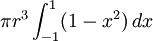
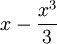
![\ Pi r ^ 3 \ cdot [1-1 / 3 - (- 1 + 1/3)]](../../images/206/20619.png) =
= 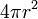 . El volumen de la esfera consiste en capas de losas esféricas infinitesimales, y el volumen de la esfera es igual a
. El volumen de la esfera consiste en capas de losas esféricas infinitesimales, y el volumen de la esfera es igual a 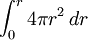 =
= 