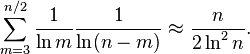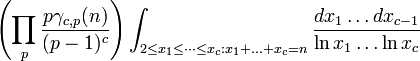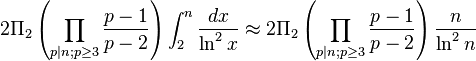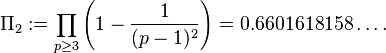La conjetura de Goldbach

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

Esta selección se hace para las escuelas por caridad para niños leer más . ¿Quieres saber sobre el patrocinio? Ver www.sponsorachild.org.uk

La conjetura de Goldbach es uno de los más antiguos problemas sin resolver en la teoría de números y en todas las matemáticas . Dice lo siguiente:

Cada incluso número entero mayor que 2 puede escribirse como la suma de dos números primos .

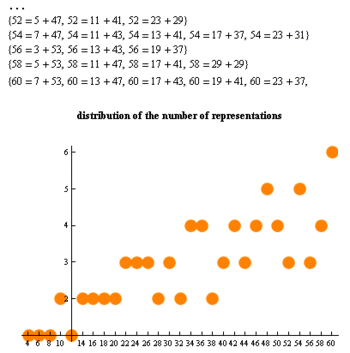
La expresión de un número dado incluso como una suma de dos números primos se llama un Goldbach partición del número. Por ejemplo,

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7

...

En otras palabras, la conjetura de Goldbach afirma que cada número incluso mayor que o igual a cuatro es un número Goldbach, un número que puede expresarse como la suma de dos números primos. Ver también La conjetura de Levy.

Una ilustración de la conjetura de Goldbach.

Orígenes

En 7 de junio de 1742, la Prusiana matemático Christian Goldbach escribió una carta a Leonhard Euler (carta XLIII) en el que propuso la siguiente conjetura:

Cada número entero mayor que 2 puede escribirse como la suma de tres números primos.

Consideró 1 a ser un número primo , una convención posteriormente abandonado. Una versión moderna de la conjetura de Goldbach inicial es:

Cada número entero mayor que 5 puede escribirse como la suma de tres números primos.

Euler, de interesarse en el problema, respondió señalando que esta conjetura es equivalente con otra versión:

Cada entero par mayor que 2 puede escribirse como la suma de dos números primos,

agregando que él consideraba esto un todo seguro teorema ("ein ganz gewisses Theorema"), a pesar de su incapacidad para demostrarlo.

Versión de Euler es la forma en la que la conjetura se expresa por lo general en la actualidad. También se conoce como el " fuerte "," incluso ", o" binario "conjetura de Goldbach, para distinguirlo de un corolario más débil. El fuerte conjetura de Goldbach implica la conjetura de que todos los números impares mayores que 7 son la suma de tres primos impares, lo que hoy se conoce indistintamente como la "Débil" conjetura de Goldbach, el "extraño" Goldbach conjetura, o la "ternario" Conjetura de Goldbach. Ambas cuestiones han quedado sin resolver desde entonces, a pesar de la forma débil de la conjetura parece ser mucho más cercano a la resolución de la fuerte. Si el fuerte conjetura de Goldbach es verdadera, la conjetura débil de Goldbach será verdad por implicación.

Resultados verificados

Para valores pequeños de n, el fuerte conjetura de Goldbach (y por tanto la conjetura débil de Goldbach) pueden verificarse directamente. Por ejemplo, N. Pipping en 1938 verificó laboriosamente la conjetura hasta 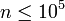$n \ leq 10 ^ 5$ . Con la llegada de las computadoras, muchos más pequeños valores de n se han comprobado; T. 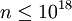Oliveira e Silva está ejecutando una búsqueda informática distribuida que ha verificado la conjetura de $n \ leq 10 ^ {18}$ .

La conjetura de Goldbach no dice que un número debe ser la suma de un único par de números primos. Los ejemplos de este artículo muestran que más de un par de números primos puede resumir con el mismo número.

Justificación heurística

Consideraciones estadísticas que se centran en la distribución probabilística de los números primos pruebas informal presente en favor de la conjetura (tanto en las formas débiles y fuertes) para suficientemente grandes números enteros: cuanto mayor es el número entero, los más formas no están disponibles para ese número para ser representada como la suma de otros dos o tres números, y la más "probable" se hace que al menos una de estas representaciones se compone enteramente de números primos .

Número de maneras de escribir un número par n como la suma de dos números primos (4 ≤ n ≤ 1,000)

Número de formas de escribir un número par n como la suma de dos números primos (4 ≤ n ≤ 1.000.000)

Una versión muy cruda de la argumento probabilístico heurístico (para la forma fuerte de la conjetura de Goldbach) es como sigue. La teorema del número primo afirma que un m entero seleccionado al azar tiene más o menos un 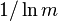$1 / \ ln m \, \!$ posibilidad de ser primo. Así, si n es un número entero grande, incluso y m es un número entre 3 y n / 2, entonces uno podría esperar que la probabilidad de m y la MN siendo a la vez primordial para estar $1 \ grande / \ grande [\ ln m \, \ ln (n-m) \ grande]$ . 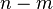Esta heurística no es riguroso para un número de razones; por ejemplo, se supone que los eventos que M y $n-m$ son primos son estadísticamente independientes entre sí. Sin embargo, si uno persigue esta heurística, uno podría esperar que el número total de maneras de escribir un gran n entero par como la suma de dos primos impares sea más o menos

$\ Sum_ {m = 3} ^ {n / 2} \ frac {1} {\ ln m} {1 \ over \ ln (nm)} \ aprox \ frac {n} {2 \ ln ^ 2 n}.$

Desde esta cantidad tiende a infinito cuando n aumenta, esperamos que cada número entero grande, incluso tiene no sólo una representación como la suma de dos números primos, pero en realidad tiene muy muchos de tales representaciones.

El argumento heurístico anterior es en realidad algo inexacto, porque ignora cierta dependencia entre los eventos de m y 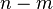$n-m$ siendo primordial. Por ejemplo, si m es impar entonces 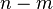$n-m$ También es extraño, y si m es par, entonces 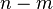$n-m$ incluso, una relación no trivial porque (además de 2) sólo números impares puede ser primordial. Del mismo modo, si n es divisible por 3, y m era ya un primer distinto de 3, entonces 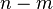$n-m$ sería también coprimeros a 3 y por lo tanto ser ligeramente más probabilidades de ser primo de un número general. 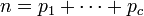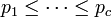Persiguiendo este tipo de análisis con más cuidado, Hardy y Littlewood en 1923 conjeturó (como parte de su famosa Hardy-Littlewood tupla primer conjetura) que para cualquier fijo c ≥ 2, el número de representaciones de un gran número entero n como la suma de los números primos c $n = p_1 + \ dotsb + p_c$ con $p_1 \ leq \ dotsb \ leq p_c$ debería ser asintóticamente igual a

$\ Left (\ prod_p \ frac {p \ gamma_ {c, p} (n)} {(p-1) ^ c} \ right) \ int_ {2 \ leq x_1 \ leq \ dotsb \ leq X_c: x_1 + \ ldots + X_c = n} \ frac {dx_1 \ ldots dx_ {c-1}} {\ ln x_1 \ ldots \ ln X_c}$

donde el producto es sobre todos los números primos p, y 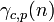$\ Gamma_ {c, p} (n)$ es el número de soluciones de la ecuación 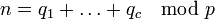$n = q_1 + \ ldots + q_c \ mod p$ en la aritmética modular , con sujeción a la restricciones 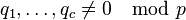$q_1, \ ldots, q_c \ neq 0 \ mod p$ . Esta fórmula ha sido rigurosamente probado ser asintóticamente válida para c ≥ 3 de los trabajos de Vinogradov, pero sigue siendo sólo una conjetura cuando 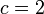$c = 2$ . En este último caso, la fórmula anterior se simplifica a 0 cuando n es impar, y para

$2 \ Pi_2 \ dejó (\ prod_ {p | n; p \ geq 3} \ frac {p-1} {p-2} \ right) \ int_2 ^ n \ frac {dx} {\ ln ^ 2 x} \ aprox 2 \ Pi_2 \ dejó (\ prod_ {p | n; p \ geq 3} \ frac {p-1} {p-2} \ right) \ frac {n} {\ ln ^ 2 n}$

cuando n es par, donde 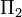$\ Pi_2$ es el constante primos gemelos

$\ Pi_2: = \ {prod_ p \ geq 3} \ left (1 - \ frac {1} {(p-1) ^ 2} \ right) = 0,6601618158 \ ldots.$

Este asintótica es a veces conocido como la conjetura de Goldbach extendida. La fuerte conjetura de Goldbach es de hecho muy similar a la Conjetura de los números primos gemelos, y los dos conjeturas se cree que son de dificultad más o menos comparable.

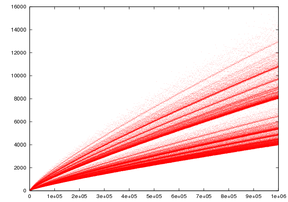
Las funciones de partición que se muestran aquí se pueden mostrar como histogramas que ilustran informativamente las ecuaciones anteriores. Ver Cometa de Goldbach.

Resultados rigurosos

La conjetura débil de Goldbach está bastante cerca de la resolución.

La fuerte conjetura de Goldbach es mucho más difícil. El trabajo de Vinogradov en 1937 y Theodor Estermann (1902-1991) en 1938 mostró que casi todos los números pares se pueden escribir como la suma de dos números primos (en el sentido de que la fracción de los números pares que pueden ser tan escriben tiende hacia 1). En 1930, Lev Schnirelmann demostró que todo número par n ≥ 4 se pueden escribir como la suma de un máximo de 300.000 números primos. Este resultado fue posteriormente mejorado por muchos autores; Actualmente, el resultado más conocido es debido a Olivier Ramare, que en 1995 mostraron que cada número par n ≥ 4 es, de hecho, la suma de a lo sumo seis números primos. De hecho, la resolución de la conjetura débil de Goldbach también implica directamente que todo número par n ≥ 4 es la suma de a lo sumo cuatro números primos.

Chen Jingrun mostró en 1973 utilizando los métodos de la teoría de que cada tamiz suficientemente grande número par puede escribirse como la suma de cualquiera de dos números primos, o un primer y un semiprimo (el producto de dos números primos) -por ejemplo, 100 = 23 + 7 · 11.

En 1975, Hugh Montgomery y Robert Charles Vaughan mostró que "la mayoría" de los números pares eran expresable como la suma de dos números primos. Más precisamente, mostraron que existía constantes positivas 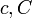$c, C$ de tal manera que para todos los números N suficientemente grande, cada número incluso menor que N es la suma de dos números primos, con a lo sumo 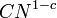$C N ^ {1-c}$ excepciones. En particular, el conjunto de los enteros incluso que no son la suma de dos números primos tiene densidad cero.

Roger Heath-Brown y Jan-Christoph Schlage-Puchta mostró en 2002 que cada suficientemente grande entero par es la suma de dos números primos y exactamente 13 potencias de 2.

Uno puede plantear preguntas similares cuando los números primos son reemplazados por otros conjuntos especiales de números, como los cuadrados. Por ejemplo, era probado por Lagrange que cada número entero positivo es la suma de cuatro cuadrados. Ver El problema de Waring.

Intento de pruebas

Al igual que con muchas conjeturas famosos en matemáticas, hay una serie de supuestas pruebas de la conjetura de Goldbach, ninguno de los cuales están actualmente aceptado por la comunidad matemática.

Debido a que es fácil de entender por los laicos, la conjetura de Goldbach es un destino popular para los matemáticos aficionados, que a menudo tratan de probar o refutar que utilizando sólo matemáticas a nivel de la escuela secundaria. Comparte este destino con el teorema de cuatro colores y el último teorema de Fermat , los cuales también tienen un problema fácil de fijar, pero sin embargo parece ser solucionable sólo a través de métodos extraordinariamente elaboradas.

En la cultura popular

Para generar publicidad para el libro El tío Petros y la conjetura de Goldbach por Apostolos Doxiadis, editor británico Tony Faber ofreció un premio de $ 1.000.000 para una demostración de la conjetura en 2000, si una prueba se presentó antes de abril de 2002. El premio nunca fue reclamado.
El drama de la televisión Lewis contó con un profesor de matemáticas en la Universidad de Oxford que había ganado el Los campos medalla por su trabajo en la conjetura de Goldbach, que era una característica principal argumento.
El cuento de Isaac Asimov "Sesenta Millones Trillones Combinaciones" presentó un matemático que sospechaba que su trabajo en la conjetura de Goldbach había sido robado.
En el Película española "La habitación de Fermat" (2007), dirigida por Luis Piedrahita y Rodrigo Sopeña, un joven matemático afirma haber resuelto la conjetura.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Goldbach%27s_conjecture&oldid=208155239 "

We provide Linux to the World