
Entero
Acerca de este escuelas selección Wikipedia
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países

Los números enteros (de la América entera, lo que significa que con integridad intacta, entero) son el conjunto de números que constan de los números naturales , incluyendo 0 ( 0 , 1 , 2, 3, ...) y sus negativos (0, -1, -2, -3, ...). Son números que se pueden escribir sin un componente fraccionario o decimal, y caen dentro del conjunto {... -2, -1, 0, 1, 2, ...}. Por ejemplo, 65, 7, y -756 son números enteros; 1.6 y 1½ no son números enteros. En otros términos, los enteros son los números que puede contar con elementos tales como las manzanas o los dedos, y sus aspectos negativos, incluyendo 0.
Más formalmente, los enteros son la única dominio integral cuyos elementos son positivos bien ordenado, y en qué orden se conserva por adición . Al igual que los números naturales, los enteros forman un conjunto infinito numerable. La conjunto de todos los números enteros a menudo se indica mediante un negrita Z (o pizarra negrita 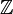 , Unicode U + 2124), lo que significa Zahlen ( alemán para los números).
, Unicode U + 2124), lo que significa Zahlen ( alemán para los números).
En teoría algebraica de números, estos enteros comúnmente entendidos, incrustado en el campo de los números racionales , se hace referencia a los enteros racionales para distinguirlos de la forma más amplia definida enteros algebraicos.
Propiedades algebraicas
Al igual que los números naturales, Z es cerrado bajo la operaciones de adición y multiplicación , es decir, la suma y el producto de dos enteros es un número entero. Sin embargo, con la inclusión de los números naturales negativos, y, sobre todo, cero , Z (a diferencia de los números naturales) también se cierra bajo la resta . Z no está cerrada bajo la operación de división , ya que el cociente de dos números enteros (por ejemplo, 1 dividido por 2), no se necesita ser un entero.
A continuación se enumeran algunas de las propiedades básicas de suma y multiplicación para cualquier enteros a, b y c.
| adición | multiplicación | |
| cierre: | a + b es un número entero | a × b es un número entero |
| asociatividad : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| conmutatividad : | a + b = b + a | a × b = b × a |
| existencia de una elemento de identidad: | a + 0 = a | a × 1 = a |
| existencia de elementos inversos: | a + (- a) = 0 | |
| distributividad: | a × (b + c) = (a × b) + (a × c) | |
| No divisores de cero: | Si ab = 0, entonces o bien a = 0 o b = 0 (o ambos) | |
En el lenguaje del álgebra abstracta , los primeros cinco propiedades mencionadas anteriormente para la adición dicen que Z bajo la adición es una grupo abeliano. Como grupo bajo la adición, Z es un grupo cíclico , ya que cada número entero distinto de cero puede ser escrita como una suma finita 1 + 1 + 1 o ... (-1) + (-1) + ... + (-1) . De hecho, Z bajo la adición es el único grupo cíclico infinito, en el sentido de que cualquier grupo cíclico infinito es isomorfo a Z.
Los primeros cuatro propiedades mencionadas anteriormente para la multiplicación dicen que Z bajo la multiplicación es una monoide conmutativo. Sin embargo, tenga en cuenta que no todo entero tiene un inverso multiplicativo; por ejemplo, no hay x número entero tal que 2 x = 1, debido a que el lado izquierdo es par, mientras que el lado derecho es impar. Esto significa que Z bajo la multiplicación no es un grupo.
Todas las reglas de la tabla de propiedades anteriormente, a excepción de la última, tomados juntos dicen que Z junto con la suma y la multiplicación es un conmutativa sonar con la unidad. Adición de la última propiedad dice que Z es un dominio integral. De hecho, Z proporciona la motivación para definir una estructura de este tipo.
La falta de inversos multiplicativos, que es equivalente al hecho de que Z no está cerrada en la división, significa que Z no es una campo. El campo más pequeño que contiene los números enteros es el campo de los números racionales . Este proceso puede ser imitado para formar el campo de fracciones de cualquier dominio integral.
Aunque la división ordinaria no está definido en Z, no poseen una propiedad importante llamado algoritmo de la división: es decir, le dieron dos números enteros a y b con b ≠ 0, existen enteros únicos q y r tales que a = q × b + r y 0 ≤ r <| b |, donde | b | denota el valor absoluto de b. El número entero q se llama el cociente y r se llama resto, que resulta de la división de a entre b. Esta es la base para la Algoritmo de Euclides para calcular máximo común divisor .
Una vez más, en el lenguaje del álgebra abstracta, lo anterior dice que Z es un Dominio euclidiana. Esto implica que Z es una dominio de ideales principales y cualquier número entero positivo se puede escribir como el producto de números primos de una manera esencialmente único. Este es el teorema fundamental de la aritmética .
Propiedades de orden teórico
Z es una conjunto totalmente ordenado y sin límite superior o inferior. El ordenamiento de Z está dada por
- ... <-2 <-1 <0 <1 <2 <...
Un entero es positivo si es mayor que cero y negativo si es menor que cero. Zero se define como ni negativo ni positivo.
El orden de los números enteros es compatible con las operaciones algebraicas de la siguiente manera:
- si a <b y c <d, entonces a + c <b + d
- si a <b y 0 <c, entonces ac <bc. (A partir de este hecho, se puede demostrar que si c <0, entonces ac> bc.)
De ello se deduce que Z junto con el ordenamiento anterior es un anillo de pedida.
Construcción
Los enteros pueden ser construidos a partir de los números naturales mediante la definición clases de equivalencia de pares de números naturales N × N bajo una relación de equivalencia , "~", donde
precisamente cuando
Teniendo 0 ser un número natural, los números naturales pueden ser considerados para ser números enteros por parte de la incrustación de que los mapas de n [(n, 0)], donde [(a, b)] denota la clase de equivalencia que tiene (a, b) como un miembro.
La adición y multiplicación de números enteros se definen como sigue:
Se comprueba fácilmente que el resultado es independiente de la elección de los representantes de las clases de equivalencia.
Típicamente, [(a, b)] se denota por
donde
Si los números naturales se identifican con los números enteros correspondientes (usando la incrustación se ha mencionado anteriormente), esta convención no crea ninguna ambigüedad.
Esta notación se recupere lo familiar la representación de los números enteros como {..., - 3, -2, -1,0,1,2,3, ...}.
Algunos ejemplos son:
Los enteros en informática
Un número entero (a veces conocido como un "int", del nombre de un tipo de datos en el lenguaje de programación C ) es a menudo una primitiva tipo de datos en lenguajes de programación . Sin embargo, los tipos de datos enteros sólo pueden representar un subconjunto de todos los enteros, ya que las computadoras son prácticos de capacidad finita. También, en el común representación de complemento a dos, la definición inherente signo que distingue entre "negativo" y "no negativo" en lugar de "negativo, positivo y 0". (Es, sin embargo, ciertamente posible para un ordenador para determinar si un valor entero es realmente positiva).
Representaciones de longitud variable de enteros, como bignums, pueden almacenar cualquier número entero que cabe en la memoria del ordenador. Otros tipos de datos enteros se implementan con un tamaño fijo, por lo general un número de bits que es una potencia de 2 (4, 8, 16, etc.) o un número memorable de dígitos decimales (por ejemplo, 9 o 10).
En contraste, los modelos teóricos de los ordenadores digitales , tales como Máquinas de Turing, por lo general no tienen infinita (pero sólo sin límites finitos) de capacidad.
Cardinalidad
La cardinalidad del conjunto de los enteros es igual a 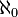 . Esto se demuestra fácilmente mediante la construcción de una biyección, es decir, una función que es inyectiva y surjective de
. Esto se demuestra fácilmente mediante la construcción de una biyección, es decir, una función que es inyectiva y surjective de 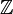 a
a 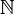 . Considere la función
. Considere la función
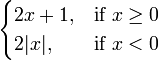 .
.
Si el dominio está restringido a 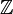 entonces cada uno de los miembros de
entonces cada uno de los miembros de  tiene una y sólo una miembro correspondiente de
tiene una y sólo una miembro correspondiente de  y por la definición de igualdad cardenal los dos conjuntos tienen la misma cardinalidad.
y por la definición de igualdad cardenal los dos conjuntos tienen la misma cardinalidad.

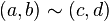
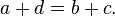
![[(A, b)] + [(c, d)]:. = [(A + c, b + d)] \,](../../images/94/9425.png)
![[(A, b)] \ cdot [(c, d)]:. = [(Ac + bd, ad + bc)] \,](../../images/94/9426.png)
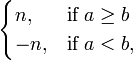
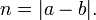
![\ Begin {align} 0 & = [(0,0)] y = [(1,1)] & = \ cdots & & = [(k, k)] \\ 1 & = [(1,0)] & = [(2,1)] y = \ cdots & & = [(k + 1, k)] -1 \\ & = [(0,1)] y = [(1,2)] y = \ cdots & & = [(k, k + 1)] 2 \\ & = [(2,0)] y = [(3,1)] y = \ cdots & & = [(k + 2, k)] \\ -2 & = [(0,2)] y = [(1,3)] & = \ cdots & & = [(k, k + 2)] \ end {align}](../../images/94/9429.png)
