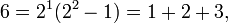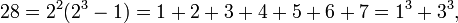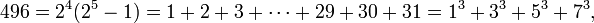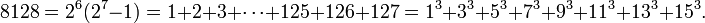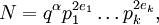Nombre parfait

Contexte des écoles Wikipédia

Les articles de cette sélection écoles ont été organisés par sujet du programme d'études grâce aux bénévoles d'enfants SOS. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .

Ensembles d'entiers base divisibilité-

Vue d'ensemble	Factorisation Entier Diviseur Diviseur unitaire Fonction diviseur Premier facteur Théorème fondamental de l'arithmétique

Les formes de factorisation	Nombre premier Numéro Composite Nombre semi-premier numéro Nombre oblong Nombre sphénique Numéro sans Square- Nombre puissant Puissance parfaite Numéro d'Achille Nombre lisse Nombre régulier Chiffre approximatif Nombre inhabituel

Sommes contraints de diviseurs	Nombre parfait Nombre presque parfait Nombre quasi parfait Nombre parfait multiple numéro de Hemiperfect Nombre hyperparfait Numéro Superperfect Nombre parfait unitaire Nombre semi-parfait Numéro Pratique

Avec de nombreux diviseurs	Nombre abondant Nombre abondant Primitive Nombre hautement abondant Nombre superabondant Nombre colossalement abondant Nombre hautement composé Nombre hautement composé Supérieur Nombre étrange

Relatif à séquences aliquotes	Nombre intouchable Numéro amiable Nombre sociable Numéro fiancée

Autres séries	Nombre déficient Numéro bienvenus Numéro solitaire Nombre sublime Numéro de diviseur harmonique Nombre frugal Nombre équidigital Nombre extravagant

En mathématiques, un nombre parfait est défini comme un entier positif qui est la somme de ses propres positifs diviseurs , ce est la somme des diviseurs positifs non compris le nombre lui-même. De manière équivalente, un nombre parfait est un nombre qui est la moitié de la somme de tous ses diviseurs positifs, ou σ (n) = 2 n.

Le premier numéro est parfaite 6, parce que 1, 2, et 3 sont ses diviseurs positifs appropriés et 1 + 2 + 3 = 6. Le prochain numéro est parfaite 28 = 1 + 2 + 4 + 7 + 14. Les prochaines nombres parfaits sont 496 et 8128 (séquence A000396 dans OEIS ).

Ces quatre premiers nombres parfaits sont les seuls connus au début Mathématiques grecques.

Même nombres parfaits

Euclide a découvert que les quatre premiers nombres parfaits sont générés par la formule 2 ^{n -1} (2 ⁿ - 1):

pour n = 2: ¹ 2 (février ^2-1) = 6

pour n = 3: 2 ^{2 (3-1} février) = 28

pour n = 5: 2 ^{4 (5-1} février) = 496

pour n = 7: 2 ^{6 (7 à} 1 février) = 8,128.

Remarquant que 2 ⁿ - 1 est un nombre premier , dans chaque cas, Euclide a prouvé que la formule 2 ^{n -1} (2 ⁿ - 1) donne un nombre pair parfait chaque fois 2 ⁿ - (. Euclide, Prop IX.36) 1 est premier .

Mathématiciens anciens ont fait de nombreuses hypothèses sur les nombres parfaits basés sur les quatre qu'ils savaient, mais la plupart de ces hypothèses seraient plus tard se révéler inexactes. L'une de ces hypothèses est que depuis 2, 3, 5 et 7 sont précisément les quatre premiers nombres premiers, le cinquième nombre idéal serait obtenu lorsque n = 11, la cinquième écoute. Cependant, ¹¹ à 1 fév 2047 = = 23 × 89 ne est pas premier, et donc n = 11 ne donne pas un nombre parfait. Deux autres hypothèses étaient mauvaises:

Le cinquième nombre parfait aurait cinq chiffres en base 10 depuis les premiers quatre avaient une, deux, trois et quatre chiffres respectivement.
Les nombres parfaits seraient alternativement terminer en six ou huit.

Le cinquième nombre parfait ( 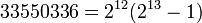$33550336 = 2 ^ {12} (2 ^ {13} -1)$ ) Dispose de 8 chiffres, réfutant ainsi la première hypothèse. Pour la seconde hypothèse, le cinquième nombre parfait se termine bien avec un 6. Toutefois, la sixième (8 589 869 056) se termine également dans un 6. Il est facile de montrer que le dernier chiffre d'un nombre pair parfaite doit être 6 ou 8 .

Dans le but de 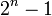$2 ^ n-1$ d'être premier, il est nécessaire, mais ne suffit pas que 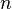$n$ devrait être premier. Les nombres premiers de la forme 2 ⁿ - 1 sont connus comme Nombres premiers de Mersenne, après le moine du XVIIe siècle Marin Mersenne, qui a étudié la théorie des nombres et nombres parfaits.

Plus d'un millénaire après Euclide, Ibn al-Haytham (Alhazen) vers 1000 AD réalisé que chaque nombre pair parfaite est de la forme 2 ^{n -1} (2 ⁿ - 1), où 2 ⁿ - 1 est premier , mais il ne était pas en mesure de prouver ce résultat. Ce ne était pas jusqu'à ce que le 18ème siècle que Leonhard Euler a prouvé que la formule 2 ^{n -1} (2 ⁿ - 1) donnera tous les numéros, même parfaites. Ainsi, il existe une association en béton d'un à un entre les nombres parfaits et même nombres premiers de Mersenne. Ce résultat est souvent dénommé "Euclide-théorème d'Euler". En Septembre 2007, seulement 44 nombres premiers de Mersenne sont connus, ce qui signifie qu'il ya 44 nombres parfaits connus, le plus grand étant de 2 × ^{32582656 (32582657} 2 - 1) avec 19.616.714 chiffres.

Les 39 premiers nombres parfaits sont même 2 ^{n -1} (2 ⁿ - 1) pour

n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917 (séquence A000043 dans OEIS )

L'autre 5 connus sont pour n = 20996011, 24036583, 25964951, 30402457, 32582657. On ne sait pas se il ya d'autres entre eux.

Il est encore incertain se il ya infinité de nombres premiers de Mersenne et nombres parfaits. La recherche de nouveaux nombres premiers de Mersenne est l'objectif de la GIMPS distribué projet de calcul.

Depuis ne importe quel nombre, même parfaite a la forme 2 ^{n -1} (2 ⁿ - 1), ce est un nombre triangulaire, et, comme tous les nombres triangulaires, ce est la somme de tous les nombres naturels jusqu'à un certain point; dans ce cas: 2 ⁿ - 1. En outre, ne importe quel nombre, même parfait, sauf le premier est la somme des deux premiers ^{(n-1) / 2} cubes impairs:

$6 = 2 ^ 1 (2 ^ 2-1) = 1 + 2 + 3, \,$

$28 = 2 ^ 2 (2 ^ 3-1) = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 1 ^ 3 ^ 3 + 3, \,$

$496 = 2 ^ 4 (2 ^ 5-1) = 1 + 2 + 3 + \ cdots + 29 + 30 + 31 = 1 ^ 3 + 3 + 3 ^ 5 ^ 3 ^ 7 + 3, \,$

$8128 = 2 ^ 6 (2 ^ 7-1) = 1 + 2 + 3 + \ cdots + 125 + 126 + 127 = 1 ^ 3 + 3 ^ 3 + 5 + 7 ^ 3 ^ 3 + 9 + 11 ^ 3 ^ 3 + 13 + 15 ^ 3 ^ 3. \,$

Même nombres parfaits (sauf 6) donnent reste 1 lorsque divisé par 9. Cela peut être reformulé comme suit. En ajoutant les chiffres de tout nombre pair parfaite (sauf 6), puis en ajoutant les chiffres du nombre résultant, et en répétant ce processus jusqu'à l'obtention d'un seul chiffre - le nombre de resuting est appelé racine numérique - produit le numéro 1. Par exemple, la racine numérique de 8128 = 1, étant donné que 8 + 1 + 2 + 8 = 19, 9 + 1 = 10 et 1 + 0 = 1.

Nombres parfaits impairs

Liste des problèmes non résolus en mathématiques
Y at-il nombres parfaits impairs?

On ne sait pas se il ya des nombres parfaits impairs. Différents résultats ont été obtenus, mais aucun qui a contribué à localiser une ou autrement résoudre la question de leur existence. Carl Pomerance a présenté un Principe d'économie qui suggère qu'aucun nombres parfaits impairs existent. En outre, il a été supposé qu'il n'y a pas impair Nombres harmoniques de minerai. Si cela est vrai, cela signifierait qu'il n'y a pas nombres parfaits impairs.

Toute étrange parfaite nombre N doit satisfaire aux conditions suivantes:

N> 10 ^300. Une recherche est à prouver que N> 10 ⁵⁰⁰ est également requise.
N est de la forme

$N = q ^ {\ alpha} ^ {p_1 2e_1} \ ldots p_k ^ {} 2e_k,$

où:

q, p _1, ..., p _k sont des nombres premiers distincts (Euler).
q ≡ α ≡ 1 ( mod 4) (Euler).
Le plus petit facteur premier de N est inférieur à (2 k + 8) / 3 (Grün 1952).
La relation 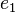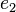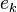$e_1$ ≡ $E_2$ ... ≡ $E K$ ≡ 1 ( mod 3) ne est pas satisfaite (McDaniel 1970).
Soit q ^α> 10 ^20, ou 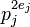$P_j ^ {} 2e_j$ > 10 ²⁰ pour certains j (Cohen 1987).
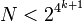$N <2 ^ {4 ^ {k + 1}}$ (Nielsen, 2003).

Le plus grand facteur premier de N est supérieur à 10 ⁸ (Takeshi Yasuo Goto et Ohno, 2006).
Le deuxième plus grand facteur premier est supérieur à 10 ^4, et le troisième plus grand facteur premier est supérieur à 100 (Iannucci 1999, 2000).
N a au moins 75 facteurs premiers; et au moins neuf facteurs premiers distincts. Si 3 ne est pas l'un des facteurs de N, N, puis a au moins 12 facteurs premiers distincts (Nielsen 2006; Kevin Hare 2005).

Quand 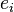≤ 2 pour chaque i
- Le plus petit facteur premier de N est au moins 739 (Cohen 1987).
- α ≡ 1 ( mod 12) ou α ≡ 9 (mod 12) (McDaniel 1970).

Citation

En 1888, Sylvester a déclaré:

... Une méditation prolongée sur le sujet m'a convaincu que l'existence de toute une telle [nombre parfait impair] -son
échapper, pour ainsi dire, de la toile complexe de conditions qui ourlent dans toutes les parties-serait peu court d'un miracle.

Résultats mineures

Même nombres parfaits ont une forme très précise; nombres parfaits impairs sont rares, si elles existent. Il ya un certain nombre de résultats sur les nombres parfaits qui sont en fait assez facile à prouver mais néanmoins impressionnante en apparence; certains d'entre eux viennent aussi sous Richard Guy loi forte des petits nombres:

Un nombre parfait impair ne est pas divisible par 105 (Kühnel 1949).
Chaque nombre parfait impair est de la forme 12 m + 1 ou 36 m (+ 9 Touchard 1953; Holdener 2002).
Le nombre que même parfaite de la forme 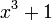$x ^ 3 + 1$ est 28 (Makowski 1962).
Un Nombre de Fermat ne peut pas être un nombre parfait (Luca 2000).
En divisant la définition par le biais par le nombre parfait N, le inverses des facteurs d'un nombre parfait N doit ajouter jusqu'à 2:
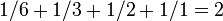- Pour 6, nous avons $6.1 + 3.1 + 2.1 + 1.1 = 2$ ;
- Pour 28, nous avons 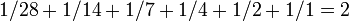$1/28 + 1/14 + 1/7 + 1/4 + 1/2 + 1/1 = 2$ , Etc.
Le nombre de diviseurs d'un nombre parfait (si pair ou impair) doit être encore, puisque N ne peut pas être un carré parfait.
- De ces deux résultats, il se ensuit que tout nombre parfait est un Numéro de l'harmonique de minerai.

Concepts associés

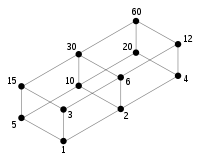
La somme des diviseurs propres donne divers autres types de numéros. Nombres, où la somme est inférieur au nombre se sont appelés déficiente, et où il est plus grand que le nombre, abondante. Ces termes, ainsi que lui-même parfait, viennent du grec la numérologie. Une paire de nombres qui sont la somme de chaque autres diviseurs propres sont appelés cycles à l'amiable, en plus importantes de numéros sont appelés sociable. Un nombre entier positif tel que tout nombre entier positif plus petit est une somme de diviseurs distincts de celui-ci est un nombre pratique.

Par définition, un nombre parfait est un point fixe de la restriction (n) = σ de la fonction de diviseur (n) - n, et la aliquote séquence associée à un nombre idéal est une constante séquence .

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Perfect_number&oldid=198739385 "

We provide Linux to the World