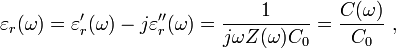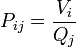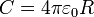Capacitance
Contexte des écoles Wikipédia
SOS Enfants produite ce site pour les écoles ainsi que ce site de vidéo sur l'Afrique . Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?
| Electromagnétisme |
|---|
 |
Électrostatique
|
Magnétostatique
|
Électrodynamique
|
Réseau électrique
|
Formulation covariante Tenseur électromagnétique ( tenseur-énergie)
|
Dans l'électromagnétisme et de l'électronique , la capacité est la capacité d'un corps à retenir une charge électrique. La capacité est également une mesure de la quantité de énergie électrique stockée (ou séparés) pour une donnée potentiel électrique. Une forme courante de dispositif de stockage d'énergie est une plaque parallèle condensateur. Dans un condensateur à plaques parallèles, la capacité est directement proportionnelle à la surface des plaques conductrices et inversement proportionnelle à la distance de séparation entre les plaques. Si les charges sur les plaques et + Q - Q et V indique la tension entre les plaques, puis la capacité est donnée par
Le Unité SI de capacité est le farad; 1 Farad est une coulomb par volts .
L' énergie (mesurée en joules) stockée dans un condensateur est égale au travail accompli pour le charger. Considérons une capacité C, la tenue d'une charge + q sur une plaque et - q de l'autre. Déplacement d'un petit élément de la charge d q d'une plaque à l'autre contre la différence de potentiel V = q / C nécessite le travail d W:
où W est le travail mesurée en joules, q est la charge mesurée en coulombs et C est la capacité, mesurée en farads.
L'énergie stockée dans un condensateur est obtenu par intégration de cette équation. A partir d'une capacité non chargé (q = 0) et déplacement des charges d'une plaque à l'autre jusqu'à ce que les plaques ont charge + Q et - Q nécessite le travail W:
Condensateurs
La capacité de la majorité des condensateurs utilisés dans les circuits électroniques est de plusieurs ordres de grandeur inférieure à celle du Farad. Les sous-unités les plus courantes de capacité en usage aujourd'hui sont les millifarad (MF), microfarad (uF), nanofarad (NF) et picofarad (pF).
La capacité peut être calculée si la géométrie des conducteurs et les propriétés diélectriques de l'isolant entre les conducteurs sont connus. Par exemple, la capacité d'un condensateur à plaques parallèles constitué de deux plaques parallèles à la fois de la zone A séparées par une distance d est sensiblement égale à ce qui suit:
où
- C est la capacité;
- A est la zone de chevauchement des deux plaques;
- ε r est la permittivité statique relative (parfois appelé la constante diélectrique) de la matière entre les plaques (pour le vide, ε r = 1);
- ε 0 est la constante électrique (de 0 ε ≈ 8,854 × 10 -12 F m -1); et
- d est la séparation entre les plaques.
La capacité est proportionnelle à la zone de recouvrement et inversement proportionnelle à la distance entre des feuilles conductrices. Les feuilles sont plus proches les uns des autres, plus la capacité. L'équation est une bonne approximation si d est petit par rapport aux autres dimensions des plaques de sorte que le champ dans le condensateur au cours de la majeure partie de sa surface est uniforme, et le champ dite franges autour de la périphérie fournit une faible contribution. En CGS unités l'équation est de la forme:
où C dans ce cas a les unités de longueur.
En combinant l'équation IS pour la capacité de l'équation ci-dessus pour l'énergie emmagasinée dans un condensateur, d'un condensateur à plaques planes l'énergie stockée est la suivante:
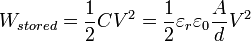 .
.
où W est l'énergie, en joules, C est la capacité, en farads; et V est la tension, en volts.
condensateurs dépendant de la tension
La constante diélectrique d'un certain nombre de changements diélectriques très utiles en tant que fonction du champ électrique appliqué, par exemple matériaux ferroélectriques, de sorte que la capacité de ces dispositifs est plus complexe. Par exemple, en chargeant un condensateur par exemple l'augmentation de la tension différentielle de charge est régie par:
où la dépendance de la tension de la capacité, C (V), vient du domaine, qui, dans un appareil à plaques parallèles de grande surface est donnée par d = ε / V. Ce champ polarise le diélectrique, qui polarisation, dans le cas d'un ferro-électrique, est un S fonction non linéaire en forme de champ, qui, dans le cas d'un dispositif à plaques parallèles de grande surface, se traduit par une capacité qui est une fonction non linéaire de la tension provoquant le terrain.
Correspondant à la capacité dépendant de la tension, pour charger le condensateur à la tension V une relation intégrale est trouvé:
ce qui concorde avec Q = CV que lorsque C est tension indépendante.
De même, l'énergie stockée dans le condensateur à présent est donnée par
Intégration:
où l'échange de la Afin d'intégration est utilisé.
La capacité non linéaire d'une sonde de microscope balayée le long d'une surface ferro-électrique est utilisé pour étudier la structure du domaine des matériaux ferroélectriques.
Un autre exemple de la capacité dépendant de la tension se produit dans des dispositifs semiconducteurs tels que les semi-conducteurs des diodes, où la dépendance de tension ne vient pas d'un changement de constante diélectrique mais dans une dépendance de la tension de l'espacement entre les charges sur les deux côtés du condensateur.
condensateurs dépendant de la fréquence
Si un condensateur est entraîné par une tension variant dans le temps qui change assez rapidement, alors la polarisation du diélectrique ne peut pas suivre le signal. A titre d'exemple de l'origine de ce mécanisme, les dipôles microscopiques internes contribuent à la constante diélectrique ne peuvent pas se déplacer instantanément, et ainsi que la fréquence d'une tension alternative appliquée augmente, la réponse de dipôle est limitée et la constante diélectrique diminue. Un changement de la constante diélectrique à la fréquence est appelée diélectrique dispersion, et est régie par processus de relaxation diélectriques, tels que Relaxation Debye. Dans des conditions transitoires, le champ de déplacement peut être exprimée comme (voir susceptibilité électrique):
indiquant le décalage en réponse à la dépendance temporelle de ε r, calculé en principe à partir d'une analyse au microscope sous-jacent, par exemple, du comportement de dipôle dans le diélectrique. Voir, par exemple, fonction de réponse linéaire. L'intégrale se étend sur l'histoire passée ensemble jusqu'à l'heure actuelle. Un Transformée de Fourier à temps, se traduit par:
où ε r (ω) est maintenant un fonction complexe, avec une partie imaginaire liés à l'absorption de l'énergie du champ par le milieu. Voir permittivité. La capacitance étant proportionnelle à la constante diélectrique, présente également ce problème de fréquence. Transformation de Fourier la loi de Gauss avec cette forme de champ de déplacement:
où j est l' unité imaginaire , V (ω) est la composante de tension à la fréquence angulaire ω, G (ω) est la partie réelle du courant, appelé la conductance, et C (ω) détermine la partie imaginaire du courant et est la capacité. Z (ω) est l'impédance complexe.
Quand un condensateur à plaques parallèles est rempli d'un diélectrique, la mesure des propriétés diélectriques du milieu est basée sur la relation:
où un seul premier désigne la partie réelle et une partie à double amorcer le imaginaire, Z (ω) est l'impédance complexe de la présente diélectrique, C (ω) est la capacité que l'on appelle un complexe avec la présente diélectrique, et C 0 est la capacité sans le diélectrique. (Mesure «sans le diélectrique« en principe un moyen de mesure dans espace libre, un objectif inatteignable dans la mesure où même le vide quantique est prévu pour présenter un comportement non idéale, comme dichroïsme. Pour des raisons pratiques, lorsque des erreurs de mesure sont prises en compte, dans une mesure souvent vide terrestre, ou simplement un calcul de C 0, est suffisamment précis. )
En utilisant cette méthode de mesure, la constante diélectrique peut présenter une résonance à certaines fréquences correspondant à des fréquences de réponse caractéristique (énergies d'excitation) de contributeurs à la constante diélectrique. Ces résonances sont la base d'un certain nombre de techniques expérimentales pour détecter des défauts. La méthode de mesure de conductance absorption en fonction de la fréquence. En variante, la réponse temporelle de la capacité peut être utilisé directement, comme dans niveau profond spectroscopie transitoire.
Un autre exemple de la capacité dépendant de la fréquence se produit avec Des condensateurs MOS, où la génération lente de porteurs minoritaires que le moyen à haute fréquence des mesures de capacitance seulement la réponse de porteurs majoritaires, alors que dans les basses fréquences les deux types de support répondre.
A des fréquences optiques, des semi-conducteurs de la structure des pièces constante diélectrique liée à la structure de bande du solide. Sophistiqué méthodes de mesure de la spectroscopie de modulation basés sur la modulation de la structure cristalline par la pression ou par d'autres contraintes et en observant les changements connexes dans l'absorption ou la réflexion de la lumière ont fait progresser notre connaissance de ces matériaux.
matrice de capacité
La discussion ci-dessus est limitée au cas de deux plaques conductrices, bien que de taille et de forme arbitraire. La définition C = Q / V détient toujours pour une seule plaque donnée une charge, dans ce cas, les lignes de champ produites par cette charge se terminent comme si la plaque ont été au centre d'une sphère de charge opposée à l'infini.
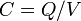 ne se applique pas quand il ya plus de deux plaques chargées, ou lorsque la charge nette sur les deux plaques est non nulle. Pour gérer ce cas, Maxwell a présenté ses «coefficients de potentiel». Si trois plaques sont donnés charges
ne se applique pas quand il ya plus de deux plaques chargées, ou lorsque la charge nette sur les deux plaques est non nulle. Pour gérer ce cas, Maxwell a présenté ses «coefficients de potentiel». Si trois plaques sont donnés charges 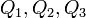 , Alors la tension de la plaque 1 est donnée par
, Alors la tension de la plaque 1 est donnée par
 ,
,
et de même pour les autres tensions. Maxwell a montré que les coefficients de potentiel sont symétriques, de sorte que 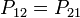 , Etc. Ainsi, le système peut être décrit par une collection de coefficients connus sous le nom "réciproque Capacité Matrix" est utilisé, qui est défini comme:
, Etc. Ainsi, le système peut être décrit par une collection de coefficients connus sous le nom "réciproque Capacité Matrix" est utilisé, qui est défini comme:
De là, la capacité mutuelle 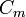 entre deux objets peuvent être définis par la résolution de la charge totale Q et l'utilisation
entre deux objets peuvent être définis par la résolution de la charge totale Q et l'utilisation 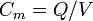 .
.
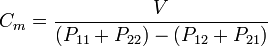
Comme aucun dispositif réel tient parfaitement charges égales et opposées sur chacun des deux «plaques», ce est la capacité mutuelle qui est rapporté sur les condensateurs. La collection de coefficients 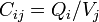 qui est connu en tant que matrice de capacité et décrit également la capacité du système.
qui est connu en tant que matrice de capacité et décrit également la capacité du système.
Auto-capacité
Dans les circuits électriques, la capacité à long terme est habituellement un raccourci pour le capacité mutuelle entre deux conducteurs adjacents, tels que les deux plaques d'un condensateur. Il existe également une propriété appelée auto-capacité, qui est le montant de la charge électrique qui doit être ajouté à un conducteur isolé à augmenter son potentiel électrique par un volt. Le point de ce potentiel de référence est une sphère théorique creuse conductrice, de rayon infini, centrée sur le conducteur. En utilisant ce procédé, la capacité propre d'une sphère de rayon R conductrice est donnée par:
Exemples de valeurs de l'auto-capacité sont:
- pour la "plaque" sommet d'une générateur de Van de Graaff, généralement une sphère de 20 cm de rayon: 20 pF
- la planète Terre : environ 700 nF
Élastance
L'inverse de la capacité est appelée élastance. L'unité de élastance est le daraf.
Capacité parasite
Les deux conducteurs adjacents peuvent être considérés comme un condensateur, bien que la capacité sera faible à moins que les conducteurs sont rapprochées pour longtemps. Cet effet (souvent indésirables) est appelé «capacité parasite". Capacité parasite peut permettre aux signaux des fuites entre les circuits autrement isolés (un effet appelé diaphonie), et il peut être un facteur limitant pour le bon fonctionnement de circuits à haute fréquence.
Capacité parasite est souvent rencontré dans les circuits d'amplification dans la forme de "traversée" capacité qui interconnecte les nœuds d'entrée et de sortie (à la fois défini par rapport à un terrain d'entente). Il est souvent pratique à des fins analytiques pour remplacer cette capacité avec une combinaison d'une capacité entrée-sol et une capacité de sortie-sol. (La configuration d'origine - y compris la capacité d'entrée-sortie - est souvent considéré comme un pi-configuration.) Le théorème de Miller peut être utilisé pour effectuer ce remplacement. Le théorème de Miller indique que, si le rapport de gain de deux noeuds est de 1 / K, puis un impédance Z reliant les deux noeuds peut être remplacé par a / (1-k) de l'impédance Z entre le premier noeud et la masse et a / (K-1) d'impédance KZ entre le second noeud et la masse. (Depuis impédance varie inversement avec la capacité, la capacité des entre-noeuds, C, sera considéré comme ayant été remplacée par une capacité de KC de l'entrée à la terre et une capacité de (K-1) C / K de la sortie à la terre.) Lorsque le le gain d'entrée-à-sortie est très grande, l'impédance d'entrée équivalent-sol est très faible alors que l'impédance de sortie-sol est sensiblement égale à la (entrée-sortie) impédance initiale.
Capacité des systèmes simples
Calcul de la capacité d'un système revient à résoudre le ∇ 2 Laplace équation φ = φ 0 avec un potentiel constant sur la surface des conducteurs. Ce est trivial dans les cas de haute symétrie. Il n'y a aucune solution en termes de fonctions élémentaires dans les cas plus complexes.
Pour les situations bidimensionnels quasi fonctions analytiques peuvent être utilisées pour mapper des géométries différentes les unes aux autres. Voir également Cartographie Schwarz-Christoffel.
| Type | Capacitance | Commentaire |
|---|---|---|
| Condensateur à plaques parallèles | 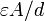 | A: Espace d: Distance ε: Permittivité |
| Câble coaxial | 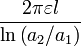 | 1: Rayon interne 2: Rayon extérieur 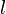 : Longueur : Longueur |
| Paire de fils parallèles | 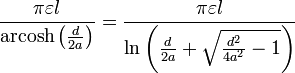 | a: rayon de fil d: Distance, d> 2a 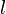 : Longueur de la paire : Longueur de la paire |
| Fil parallèle à mur | 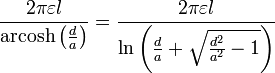 | a: rayon de fil d: Distance, d> une 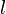 : Longueur du fil : Longueur du fil |
| Deux parallèles bandes coplanaires | 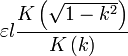 | d: Distance w 1, w 2: Largeur de la bande k i: d / (2W I + D) k 2: k 1 k 2 |
| Sphères concentriques | 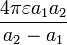 | 1: Rayon interne 2: Rayon extérieur |
| Deux sphères, rayon égal | 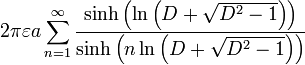 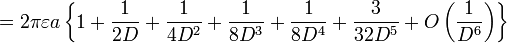 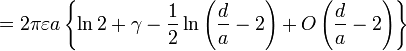 | a: Radius d: Distance, d> 2a D = d / 2a γ: La constante d'Euler |
| Sphère en face de la paroi | 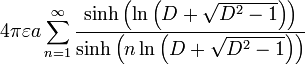 | a: Radius d: Distance, d> une D = d / a |
| Sphère | 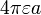 | a: Radius |
| Disque circulaire | 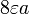 | a: Radius |
| Fil droit Thin, longueur finie | ![\ Frac {2 \ pi \ varepsilon l} {\ lambda} \ left \ {1+ \ frac {1} {\ lambda} \ left (1- \ ln 2 \ right) + \ frac {1} {\ lambda ^ {2}} \ left [1+ \ left (1- \ ln 2 \ right) ^ {2} - \ frac {\ pi ^ {2}} {12} \ right] + O \ left (\ frac {1 } {\ lambda ^ {3}} à droite) \ right \ \}](../../images/786/78639.png) | a: rayon de fil 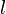 : Longueur : Longueur Λ: ln ( 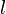 / A) / A) |

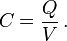
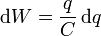
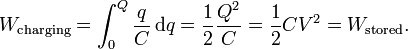
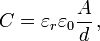
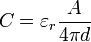
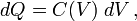
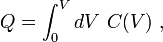
![dW = Q dV = \ left [\ ^ int_0 V \ DV '\ C (V') \ right] \ DV \.](../../images/786/78608.png)
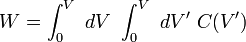
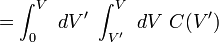
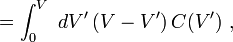
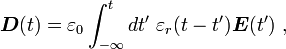
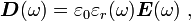
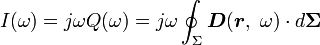
![= \ Left [G (\ omega) + j \ omega C (\ omega) \ right] V (\ omega) = \ frac {V (\ omega)} {Z (\ omega)} \,](../../images/786/78615.png)