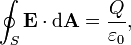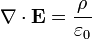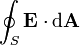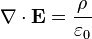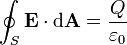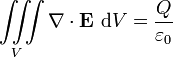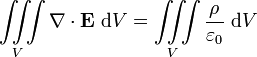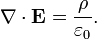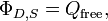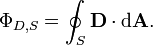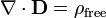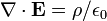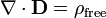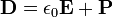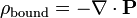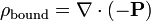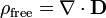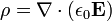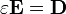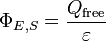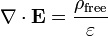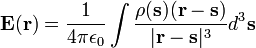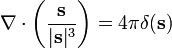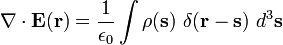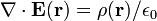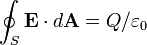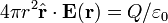La loi de Gauss

Electromagnétisme
Électricité Magnétisme
Électrostatique Charge électrique Électricité statique Champ électrique Conducteur Isolant Triboélectricité Décharge électrostatique Induction La loi de Coulomb La loi de Gauss Flux électrique / énergie potentielle Moment dipolaire électrique Polarisation
Magnétostatique La loi d'Ampère Champ magnétique Magnétisation Flux magnétique Loi de Biot-Savart Moment de dipôle magnétique La loi de Gauss à magnétisme
Électrodynamique Droit de la force de Lorentz Induction électromagnétique La loi de Faraday La loi de Lenz Déplacement actuel Les équations de Maxwell Champ électromagnétique Un rayonnement électromagnétique Tenseur de Maxwell Vecteur de Poynting Potentiel Liénard-Wiechert Les équations de Jefimenko À courant de Foucault
Réseau électrique Courant électrique Potentiel électrique Tension Résistance La loi d'Ohm circuit de la série Circuit parallèle Courant continu Courant alternatif Force électromotrice Capacitance Inductance Impédance Cavités résonnantes Guides d'ondes
Formulation covariante Tenseur électromagnétique ( tenseur-énergie) Four à courant continu Potentiel électromagnétique à quatre
Les scientifiques Ampère Coulomb Faraday Gauss Heaviside Henri Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

Dans la physique , de la loi, également connu sous le théorème de Gauss Gauss flux, est une loi relative à la distribution des charges électriques résultant au champ électrique . La loi de Gauss stipule que:

La loi a été formulée par Carl Friedrich Gauss en 1835, mais n'a pas été publié jusqu'en 1867. Il est l'un des quatre équations de Maxwell qui forment la base de électrodynamique classique, les trois autres étant La loi de Gauss pour le magnétisme, La loi d'induction de Faraday, et La loi d'Ampère avec correction de Maxwell. La loi de Gauss peut être utilisée pour dériver la loi de Coulomb , et vice versa.

La loi de Gauss peut être exprimé sous sa forme intégrale:

où le côté gauche de l'équation est une intégrale de surface désignant le flux électrique à travers une surface fermée S, et le côté droit de l'équation est la charge totale délimitée par S divisé par le constante électrique.

La loi de Gauss a aussi une forme différentielle:

· ∇ où E est le divergence du champ électrique , et ρ est la la densité de charge.

Les formes intégrales et différentielles sont liés par le théorème de la divergence, aussi appelé le théorème de Gauss. Chacune de ces formes peut aussi être exprimée de deux façons: en termes de relation entre le champ électrique E et la charge électrique totale, ou en termes de champ électrique de déplacement D et le charge électrique libre.

La loi de Gauss a une similitude mathématique étroite avec un certain nombre de lois dans d'autres domaines de la physique, comme La loi de Gauss pour le magnétisme et Théorème de Gauss. En fait, ne importe quel " loi de l'inverse carré "peut être formulé d'une manière similaire à la loi de Gauss: Par exemple, la loi de Gauss se est essentiellement équivalente à l'inverse du carré loi de Coulomb , et Théorème de Gauss est essentiellement équivalente à l'inverse du carré La loi de la gravitation de Newton.

La loi de Gauss peut être utilisé pour démontrer que tous les champs électriques à l'intérieur d'un Cage de Faraday ont une charge électrique. La loi de Gauss est quelque chose d'un analogue électrique La loi d'Ampère, qui traite avec le magnétisme.

En termes de charge totale

Forme intégrale

Pour un volume V de surface S, la loi de Gauss indique que

où Φ _{E, S} est le flux électrique à travers S, Q est la charge totale à l'intérieur V, et ε ₀ est la constante électrique. Le flux électrique est donnée par un surface intégrale sur S:

où E est le champ électrique, d A est un vecteur représentant un élément infinitésimal de la zone , et représente l'· produit scalaire ..

Application de la forme intégrale

Si le champ électrique est connu partout, la loi de Gauss, il est assez facile, en principe, de trouver la répartition de la charge électrique: La charge dans une région donnée peut être déduite en intégrant le champ électrique pour trouver le flux.

Cependant, beaucoup plus souvent, ce est le problème inverse qui doit être résolu: la distribution de charge électrique est connue, et le champ électrique a besoin d'être calculée. Ce est beaucoup plus difficile, car si vous connaissez le flux total à travers une surface donnée, qui donne presque aucune information sur le champ électrique, qui (pour tout ce que vous savez) pourrait aller dans et hors de la surface dans les modèles arbitrairement compliquées.

Une exception est se il ya une symétrie dans la situation, qui exige que le champ électrique traverse la surface de manière uniforme. Ensuite, si le flux total est connu, le champ lui-même peut en déduire à chaque point. Des exemples courants de symétries qui se prêtent à la loi de Gauss comprennent symétrie cylindrique, la symétrie plane, et la symétrie sphérique. Voir l'article Surface de Gauss pour des exemples où ces symétries sont exploitées pour calculer les champs électriques.

Forme différentielle

En forme différentielle , la loi de Gauss déclare:

où ∇ · désigne divergence, E est le champ électrique, et ρ est la totale électrique la densité de charge (y compris les frais à la fois libre et lié), et ε ₀ est la constante électrique. Ce est mathématiquement équivalente à la forme intégrale, en raison de la théorème de la divergence.

Équivalence des formes intégrales et différentielles

Les formes intégrales et différentielles sont mathématiquement équivalente, par le théorème de la divergence. Voici l'argument plus spécifiquement:

La forme intégrale de la loi de Gauss est:

pour toute surface fermée S contenant une charge Q. Par le théorème de la divergence, cette équation est équivalente à:

pour tout volume V contenant une charge Q. Par la relation entre la charge et la densité de charge, cette équation est équivalente à:

pour chaque volume V. Pour cette équation pour être simultanément vraies pour chaque volume V possible, il est nécessaire (et suffisante) pour les intégrandes soient égaux partout. Par conséquent, cette équation est équivalente à:

Ainsi, les formes intégrales et différentielles sont équivalentes.

En termes de charge libre

Gratuit fonction de la charge liée

La charge électrique qui se pose dans les situations de manuels simples serait classé comme "charge libre" -par exemple, la charge qui est transférée dans l'électricité statique ou la charge d'un plaque de condensateur. En revanche, "la charge liée" ne se pose que dans le contexte de des matériaux diélectriques (polarisables). (Tous les matériaux sont polarisable dans une certaine mesure). Lorsque ces matériaux sont placés dans un champ électrique externe, les électrons restent liés à leurs atomes respectifs, mais se déplacent d'une distance microscopique en réponse au champ, de sorte qu'ils ne sont plus sur un côté de l'atome que l'autre. Tous ces déplacements microscopiques se additionnent pour donner une distribution nette macroscopique de charge, ce qui constitue la «charge limite".

Bien au microscope, tous les frais est fondamentalement la même, il ya souvent des raisons pratiques de vouloir traiter différemment des charges liées charge libre. Le résultat est que la loi plus «fondamentale» de Gauss, en termes de E, est parfois mis dans la forme équivalente ci-dessous, qui est en fonction de D et la charge autorisée.

Forme intégrale

Cette formulation de la loi de Gauss indique que, pour chaque volume V dans l'espace, avec la surface S, l'équation suivante est vérifiée:

où Φ _{D, S} est le flux de la déplacement de champ électrique D à S, Q et _gratuit est la charge libre contenu dans V. Le flux Φ _{D, S} est définie de manière analogue au flux Φ _{E, S} du champ électrique E à S. Plus précisément, elle est donnée par l'intégrale de surface

Forme différentielle

La forme différentielle de la loi de Gauss, impliquant la charge autorisée, déclare:

· ∇ où D est le divergence du champ de déplacement électrique, et ρ est la densité _libre sans charge électrique.

Le formulaire de différentiel et forme intégrale sont mathématiquement équivalent. La preuve consiste principalement à théorème de la divergence.

Equivalence des totaux et libres états de charge

Preuve que les formulations de la loi de Gauss en termes de charge libre sont équivalentes aux formulations impliquant charge totale.

Dans cette preuve, nous allons montrer que l'équation est équivalente à l'équation Notez que nous ne traitant qu'avec les formes différentielles, pas les formes intégrales, mais ce est suffisant, car le différentiel et formes intégrales sont équivalents dans chaque cas, par le théorème de la divergence. Nous introduisons la densité polarisation P, qui a la relation suivante pour E et D: et la relation suivante à la charge liée: Maintenant, considérons les trois équations: L'idée essentielle est que la somme des deux premières équations est la troisième équation. Ceci complète la preuve: La première équation est vrai, par définition, et donc la seconde équation est vrai si et seulement si la troisième équation est vrai. Ainsi, les deuxième et troisième équations sont équivalentes, ce qui est ce que nous voulions prouver.

Dans les matériaux linéaires

Dans homogène, isotrope, non dispersif, matériaux linéaires, il ya une belle, simple relation entre E et D:

où ε est la permittivité du matériau. Dans ces conditions, il est encore une autre paire de formulations équivalentes de la loi de Gauss:

Rapport à la loi de Coulomb

Issu de la loi de Gauss de la loi de Coulomb

La loi de Gauss peut être déduite de la loi de Coulomb , qui stipule que le champ électrique dû à un arrêt charge ponctuelle est:

où

e _r est le radiale vecteur unité,

r est le rayon, | r |,

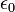est le constante électrique,

q est la charge de la particule, qui est supposé être situé à la origine.

En utilisant l'expression de la loi de Coulomb, nous obtenons le champ total au r en utilisant une partie intégrante de la somme du champ au r due à la charge infinitésimale à chaque autre point s dans l'espace, pour donner

où 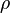est la densité de charge. Si nous prenons la divergence des deux côtés de cette équation par rapport à r, et utilisons le théorème connu

où δ (s) est la Fonction delta de Dirac, le résultat est

En utilisant le " tamisage propriété "de la fonction de Dirac, nous arrivons à

qui est la forme différentielle de la loi de Gauss, comme on le souhaite.

Notez que, depuis la loi de Coulomb se applique uniquement aux charges fixes, il ne ya aucune raison de se attendre à la loi de Gauss de tenir des frais fondé sur cette seule dérivation déplacer. En fait, la loi de Gauss ne détient des charges en mouvement, et à cet égard la loi de Gauss est plus générale que la loi de Coulomb.

Issu de la loi de Coulomb de la loi de Gauss

Strictement parlant, la loi de Coulomb ne peut être dérivé de la loi de Gauss seul, depuis la loi de Gauss ne donne aucune information concernant la boucle de E (voir Décomposition de Helmholtz et La loi de Faraday). Cependant, la loi de Coulomb peut être démontré à partir de la loi de Gauss si l'on suppose, en outre, que le champ électrique à partir d'un charge ponctuelle est sphérique symétrique (cette hypothèse, comme la loi de Coulomb lui-même, est tout à fait vrai si la charge est fixe, et approximativement vrai si la charge est en mouvement).

Prenant S dans la forme intégrale de la loi de Gauss pour être une surface sphérique de rayon r, centrée au point charge Q, nous avons

Par l'hypothèse de symétrie sphérique, l'intégrale est une constante qui peut être retiré de l'intégrale. Le résultat est

où 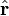est un vecteur unitaire pointant radialement à l'écart de la charge. Encore une fois par symétrie sphérique, points de E dans la direction radiale, et ainsi nous sommes

qui est essentiellement équivalente à la loi de Coulomb. Ainsi, la l'inverse du carré de dépendance de la loi du champ électrique dans la loi de Coulomb découle de la loi de Gauss.