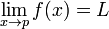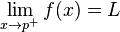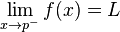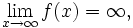Limite d'une fonction

En mathématiques , la limite d'une fonction est un concept fondamental dans le calcul et l'analyse concernant le comportement de cette fonction à proximité d'un particulier entrée. Officieusement, une fonction attribue un sortie f (x) pour chaque entrée x. La fonction a une limite L à une entrée p si f (x) est «proche» de L lorsque x est «proche» de p. En d'autres mots, f (x) deviennent de plus en plus proche de L comme x se rapprochent de plus en plus à la page. Plus précisément, lorsque f est appliqué à chaque entrée suffisamment proche de p, le résultat est une valeur de sortie qui est arbitrairement proche de L. Si les entrées "Fermer" pour p sont prises à des valeurs qui sont très différentes, la limite est dit de ne pas exister. Définitions formelles, premier conçus au début du 19ème siècle , sont donnés ci-dessous.

Histoire

Bien implicite dans le développement du calcul des 17e et 18e siècles, la notion moderne de la limite d'une fonction remonte à Bolzano qui, en 1817, a présenté les bases du epsilon-delta technique. Cependant, son travail ne était pas connu de son vivant. Cauchy discuté limites dans son Cours d'analyser (1821) et semble avoir exprimé l'essence de l'idée, mais pas de façon systématique. La première présentation publique rigoureuse de la technique a été rendu par Weierstrass dans les années 1850 et 1860 et est depuis devenu la méthode standard pour traiter les limites.

La notation écrite en utilisant l'abréviation lim avec la flèche ci-dessous est due à Hardy dans son livre Un cours de mathématiques pures en 1908.

Explication

Imaginez un avion survolant un paysage représenté par le graphe de y = f (x). Sa position horizontale est mesurée par la valeur de x, de façon similaire à la position donnée par une carte de la terre ou par un système de positionnement global. Son altitude est donnée par la coordonnée y. Il vole vers la position horizontale donnée par x = p. Comme il le fait, il se aperçoit que son altitude approches L. Si par la suite demandé de deviner l'altitude au-dessus x = p, il serait alors répondre L, même si elle ne avait jamais atteint cette position.

Qu'est-ce que cela signifie de dire que son altitude approches L? Cela signifie que son altitude se rapproche et plus proche de L, sauf pour une éventuelle petite erreur dans la précision. Par exemple, supposons que nous fixons un objectif de précision notamment pour le plan: il doit obtenir dans les dix mètres de L. Le plan rend compte qu'il peut obtenir dans les dix mètres de L, car il indique que quand il est à moins de cinquante mètres horizontaux de p, son altitude est toujours dix mètres ou moins de L.

Nous changeons donc notre objectif de précision: peut-il obtenir moins d'un mètre? Oui. Si ce est moins de sept mètres horizontaux de p, puis son altitude reste moins d'un mètre de la cible L. En résumé, pour dire que l'altitude de l'avion se approche de L que sa position horizontale approche p signifie que pour chaque objectif d'exactitude cible, il ya une zone de p dont l'altitude reste dans cet objectif de précision.

La déclaration informelle initiale peut maintenant être explicitée:

La limite d'une fonction f (x) lorsque x tend vers p est un nombre L ayant la propriété suivante: compte tenu de ne importe quelle distance de la cible à partir de L, il existe une distance de p dans lequel les valeurs de f (x) restent à l'intérieur de la distance de la cible.

Cette déclaration explicite est assez proche de la définition formelle de la limite d'une fonction à valeurs dans un espace topologique.

Définitions

Les définitions suivantes sont ceux généralement reconnus pour la limite d'une fonction dans divers contextes.

Fonctions sur la ligne réelle

Supposons que f: R → R est défini sur la ligne réelle et p, L ∈ R alors nous disent que la limite de f quand x tend vers p est L et à écrire

si et seulement si pour tout réel ε> 0, il existe un réel δ> 0 tel que 0 <| x - p | <δ implique | f (x) - L | <ε. A noter que la valeur de la limite ne dépend pas de la valeur de f (p).

Une définition plus générale se applique pour les fonctions définies sur des sous-ensembles de la ligne réelle. Soit (a, b) être un intervalle ouvert de R, et p un point de (a, b). Soit f une fonction réelle définie sur l'ensemble de (a, b) sauf peut-être à la p. On dit alors que la limite de f quand x tend vers p L est si et seulement si, pour chaque ε réel> 0, il existe un réel δ> 0 tel que 0 <| x - p | <δ et x ∈ (a, b ) implique | f (x) - L | <ε. Notez que la limite ne dépend pas de f (p) est bien définie.

Limites unilatérales

En variante peuvent se approcher x p à partir de ci-dessus (à droite) ou en dessous (à gauche), auquel cas les limites peuvent être écrites en tant que

ou

respectivement. Si ces deux limites sont égaux à L, alors cela peut être considéré comme la limite de f (x) à la p. A l'inverse, se ils ne sont pas tous deux égaux à L puis la limite, en tant que tel, ne existe pas.

Une définition formelle est la suivante. La limite de f (x) lorsque x tend vers p est au-dessus de L si, pour tout ε> 0, il existe un δ> 0 tel que | f (x) - L | <ε chaque fois que 0 <x - p <δ. La limite de f (x) lorsque x tend vers p est au-dessous de L si, pour tout ε> 0, il existe un δ> 0 tel que | f (x) - L | <ε chaque fois que 0 <p - x <δ.

Si la limite ne existe pas, il se agit d'un non-zéro oscillation.

Fonctions sur les espaces métriques

Supposons f: (M, _M d) → (N, _N d) est définie entre deux espaces métriques, avec x ∈ M, p a point de M et L ∈ N limite. Nous disons que la limite de f quand x tend vers p est L et écrivons

si et seulement si pour tout ε> 0, il existe un δ> 0 tel que, d _N (f (x), L) <ε chaque fois que 0 <d _M (x, p) <δ. Encore une fois, notez que p ne est pas nécessairement dans le domaine de f, pas plus que L besoin d'être dans la gamme de f.

Une autre définition en utilisant le concept de quartier est la suivante:

si et seulement si pour tout voisinage V de L en N, il existe un voisinage U de p dans M, tel que f (U - {p}) ⊆ V.

Fonctions sur les espaces topologiques

Supposons que X, Y sont espaces topologiques avec un Y Espace séparé. Soit p un point de limite de X, Y et L ∈. Pour une fonction f: X - {p} → Y, nous disons que la limite de f quand x tend vers p est L (ie, f (x) → L comme x → p) et écrire

si et seulement si pour tout voisinage V de L, il existe un voisinage U de p tel que f (U - {p}) ⊆ V.

A noter que le domaine de f n'a pas besoin de contenir p. Si ce est le cas, la valeur de f p est sans rapport avec la définition de la limite. La dernière partie de la définition peut également être formulée "il existe une Module: Neighbourhood_ (mathématiques) ( parler · · hist · · liens · sous-pages essais - résultats) U de p telle que f (U) ⊆ V ".

On peut formuler d'autres définitions similaires de la limite dans un espace topologique. Dans une version, le domaine de la fonction f est un sous-ensemble de Ω de l'espace topologique X. Dans ce cas, le point p doit être un point de Ω limite, et la limite est prise par rapport à la topologie induite sur Ω ( limites unilatérales, où la limite est prise à l'intérieur d'un intervalle à l'une des extrémités, sont un cas particulier de cette).

En particulier, si le domaine de f est X - {p} (ou la totalité de X), puis la limite de f en x → p existe et est égale à L si et seulement si pour tous les sous-ensembles Ω de X avec point limite p la limite de la restriction de f à Ω existe et est égale à L. Parfois, ce critère est utilisé pour établir la non-existence de la limite des deux côtés d'une fonction sur R en montrant que les limites unilatérales soit ne parviennent pas à exister ou ne sont pas d'accord. Ce point de vue est fondamentale dans le domaine de topologie générale, où les limites et la continuité en un point sont définis en termes de familles particulières de sous-ensembles, appelé les filtres, ou des séquences connues sous le nom généralisées filets.

Alternativement, l'exigence que Y un espace séparé peut être assouplie à l'hypothèse que Y un espace topologique général, mais alors la limite d'une fonction ne sera pas unique. En particulier, on ne peut plus parler de la limite d'une fonction en un point, mais plutôt une limite ou l'ensemble des limites à un point.

Une fonction est continue dans un point de limite de p et dans son domaine et seulement si f (p) est «le» (ou dans le cas général: "a") la limite de f (x) lorsque x tend vers p.

Limite d'une fonction à l'infini

La limite de cette fonction à l'infini existe.

Si le affine étendu système de nombre réel (droite réelle étendue) R est considérée, à savoir, R ∪ {-∞, + ∞}, alors il est possible de définir des limites d'une fonction à l'infini.

Si f (x) est une fonction réelle, alors la limite de f lorsque x tend vers l'infini est L, notée

si et seulement si pour tous 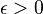il existe S> 0 tel que 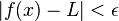lorsque x> S.

De même, la limite de f quand x tend vers l'infini est infini, notée

si et seulement si pour tout R> 0, il existe S> 0 tel que f (x)> R lorsque x> S.

D'une manière analogue, les termes suivants peuvent être définis:

.

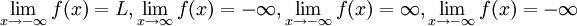Ces notions de limite une tentative de fournir une interprétation métrique de l'espace à des limites à l'infini. Toutefois, notez que ces notions d'une limite sont compatibles avec la définition de l'espace topologique de limite si

• un voisinage de -∞ est défini pour contenir un intervalle [-∞, c) où c ∈ R
• un quartier de ∞ est défini pour contenir un intervalle (c, ∞] où c ∈ R
• un voisinage de a ∈ R est défini de la manière habituelle espace métrique R

Dans ce cas, R est un espace topologique et toute fonction de la forme f: X → Y avec X, Y ⊆ R est subordonné à la définition d'une limite topologique. A noter que cette définition topologique, il est facile de définir des limites infinite finis, en des points qui ne ont pas été définies ci-dessus dans le sens métrique.

Évaluation limites à l'infini pour les fonctions rationnelles

Il ya trois règles de base pour l'évaluation des limites à l'infini pour une fonction rationnelle f (x) = p (x) / q (x):

• Si le degré de p est plus grand que le degré de q, puis la limite est infini positif ou négatif selon les signes des coefficients d'attaque;
• Si le degré de p et q sont égaux, la limite est le premier coefficient de p divisé par le premier coefficient de q;
• Si le degré de p est inférieur au degré de q, la limite est fixée à 0.

. Si la limite à l'infini existe, il représente une asymptote horizontale à x = L polynômes ne ont pas asymptotes horizontales; ils peuvent se produire avec des fonctions rationnelles.

fonctions de valeur complexe

Le plan complexe avec métrique 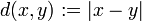est également un espace métrique. Il existe deux types de limites différentes lorsque l'on considère les fonctions à valeurs complexes.

Limite d'une fonction à un point

Si f est une fonction à valeurs complexes, puis

si et seulement si pour tout ε> 0, il existe un δ> 0 tel que pour tous les nombres réels x avec 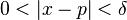, Nous avons .

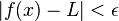Ce est juste un cas particulier de fonctions plus les espaces métriques avec M et N sont le plan complexe.

Limite d'une fonction de plusieurs variables

En notant que | x - p | représente une distance, la définition d'une limite peut être étendue aux fonctions de plusieurs variables. Dans le cas d'une fonction f: R → R ^2,

si et seulement si

pour chaque ε> 0, il existe un δ> 0 tel que pour tout (x, y) avec 0 <|| (x, y) - (p, q) || <δ, on a | f (x, y) - L | <ε

où || (x, y) - (p, q) || représente le Distance euclidienne. Cela peut être étendue à ne importe quel nombre de variables.

Propriétés

Pour dire que la limite d'une fonction f en p est L équivaut à dire

pour chaque séquence convergente _{(x n)} M avec limite égale à p, la séquence (f (x _n)) converge avec la limite L.

Si les ensembles A, B, ... forment une partition du domaine fini de fonction, , ... Et la limite relative pour chacun de ces ensembles existe et est l'égal, par exemple, L, il existe alors la limite pour le point x et est égal à L.

La fonction f est continue à la p si et seulement si la limite de f (x) lorsque x tend vers p existe et est finie. De façon équivalente, f transforme chaque séquence en M qui converge vers p dans une séquence dans laquelle N converge vers f (p).

Encore une fois, si N est un espace vectoriel normé, alors l'opération limite est linéaire dans le sens suivant: si la limite de f (x) quand x tend vers p est L et la limite de g (x) quand x tend vers p est P, puis la limite de f (x) + g (x) lorsque x tend vers p est L + P. Si a est un scalaire de la base champ, puis la limite de af (x) quand x tend vers p est Al.

Prenant la limite des fonctions est compatible avec les opérations algébriques, à condition que les limites sur les côtés droit de l'identité ci-dessous existent:

(Le dernier à condition que le dénominateur est différent de zéro). Dans chaque cas ci-dessus, lorsque les limites du droit ne existent pas, ou, dans le dernier cas, lorsque les limites à la fois dans le numérateur et le dénominateur sont égaux à zéro, néanmoins la limite sur la gauche peut encore existe - cela dépend de qui les fonctions F et G sont.

Ces règles sont également valables pour les limites d'un seul côté, pour le cas p = ± ∞, et aussi pour les limites infinies en utilisant les règles

• q + ∞ = ∞ pour q ≠ -∞
• q x ∞ = ∞ si q> 0
• q × ∞ = -∞ si q <0
• q / ∞ = 0 si q ≠ ± ∞

(Voir étendue réelle ligne de numéro).

Notez qu'il n'y a pas de règle générale pour le cas q / 0; tout dépend de la façon dont 0 est approché. Formes indéterminées - par exemple, 0/0, 0 × ∞, ∞-∞ et ∞ / ∞ - ne sont pas couverts par ces règles, mais les limites correspondantes peuvent souvent être déterminées avec Règle de L'Hôpital ou Théorème des gendarmes.