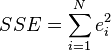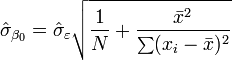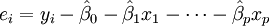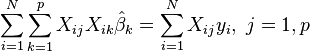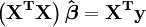A análise de regressão

Assuntos Relacionados: Matemática

Você sabia ...

Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...

A análise de regressão é uma técnica utilizada para a modelação e análise de dados numéricos consistindo de valores de um variável dependente (variável de resposta) e de um ou mais variáveis independentes (variáveis explicativas). A variável dependente na equação de regressão é modelada como uma função das variáveis independentes, correspondendo parâmetros ("constantes"), e uma termo de erro. O termo de erro é tratado como uma variável aleatória . Ela representa variação não explicada na variável dependente. Os parâmetros são estimados de forma a dar um "melhor ajuste" dos dados. Mais vulgarmente o melhor ajuste é avaliada pela utilização de mínimos quadrados método, mas outros critérios também têm sido utilizados.

Modelagem de dados pode ser utilizado sem que haja qualquer conhecimento sobre os processos subjacentes que geraram os dados; neste caso, o modelo é um modelo empírico. Além disso, no conhecimento de modelagem da distribuição de probabilidade dos erros não é necessária. A análise de regressão exige pressupostos a serem feitas a respeito de distribuição de probabilidade dos erros. Os testes estatísticos são feitos com base nestes pressupostos. Na análise de regressão, o termo "modelo" abrange tanto a função utilizada para modelar os dados e os pressupostos relativos a distribuições de probabilidade.

Regressão pode ser utilizado para predição (incluindo previsão de dados de séries temporais), inferência, teste de hipóteses, e modelagem de relações causais. Esses usos de regressão dependem fortemente de os pressupostos subjacentes estar satisfeito. A análise de regressão tem sido criticado como sendo mal utilizada para esses fins, em muitos casos em que os pressupostos apropriados não podem ser verificadas para segurar. Um fator que contribui para o mau uso de regressão é que ela pode levar consideravelmente mais habilidade para criticar um modelo do que ajustar um modelo.

História da análise de regressão

A mais antiga forma de regressão foi o método dos mínimos quadrados , que foi publicado pela Legendre em 1805, e por Gauss em 1809. O termo "mínimos quadrados" é a partir de termo de Legendre, moindres carrés. No entanto, Gauss alegou que ele havia conhecido o método desde 1795.

Legendre e Gauss tanto aplicado o método para o problema de determinar, a partir de observações astronômicas, as órbitas dos corpos sobre o sol. Euler tinha trabalhado no mesmo problema (1748), sem sucesso. Gauss publicou um maior desenvolvimento da teoria de mínimos quadrados em 1821, incluindo uma versão do Gauss-Markov teorema.

O termo "regressão" foi cunhado no século XIX para descrever um fenômeno biológico, ou seja, que a prole de indivíduos excepcionais tendem a ser, em média, menos excepcional do que seus pais e mais como seus antepassados mais distantes. Francis Galton, primo de Charles Darwin , estudou esse fenômeno e aplicou o termo um pouco enganador " regressão para a mediocridade "para ele. Para Galton, a regressão só tinha este significado biológico, mas o seu trabalho foi posteriormente prorrogado por Udny Yule e Karl Pearson para um contexto mais geral estatística. Hoje em dia o termo "regressão" é muitas vezes sinónimo de "mínimos quadrados curva de ajuste ".

Suposições subjacentes

A amostra deverá ser representativa da população para a previsão de inferência.
A variável dependente é sujeita a erro. Este erro é assumido como sendo uma variável aleatória , com uma média de zero. O erro sistemático pode estar presente, mas o seu tratamento está fora do âmbito da análise de regressão.
A variável independente é livre de erros. Se assim não for, modelagem deve ser feito usando Com erros nas variáveis técnicas modelo.
Os preditores deve ser linearmente independentes, isto é, não deve ser possível expressar qualquer preditor como uma combinação linear dos outros. Ver Multicollinear.
Os erros são não correlacionado, que é, o matriz de variância-covariância dos erros é diagonal e cada elemento diferente de zero é a variância do erro.
A variação do erro é constante ( homocedasticidade). Se não, os pesos devem ser usados.
Os erros seguem uma distribuição normal . Se não, o modelo linear generalizado deve ser usado.

Regressão linear

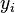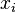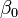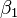Na regressão linear, a especificação do modelo é que a variável dependente, $y_i$ é um combinação linear dos parâmetros (mas não precisam de ser lineares nas variáveis independentes). Por exemplo, no modelo de regressão linear simples não é uma variável independente, $x_i$ , E dois parâmetros, $\ Beta_0$ e $\ Beta_1$ :

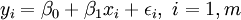
linha reta: $y_i = \ beta_0 + \ beta_1 x_i + \ epsilon_i, \ i = 1, m \!$

Na regressão linear múltipla, existem várias variáveis ou funções de variáveis independentes independentes. Por exemplo, a adição de um termo em ² x _i com a regressão anterior dá:

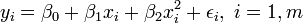
parábola: $y_i = \ beta_0 + \ beta_1 x_i + \ beta_2 x_i ^ 2 + \ epsilon_i, \ i = 1, m \!$

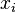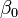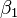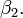
Esta ainda é a regressão linear como embora a expressão do lado direito é quadrática na variável independente $x_i$ , É linear nos parâmetros $\ Beta_0$ , $\ Beta_1$ e $\ Beta_2.$

Em ambos os casos, 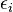$\ Epsilon_i$ é um termo de erro e o subscrito 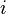$eu$ indexa uma observação particular. Dada uma amostra aleatória da população, estimamos os parâmetros populacionais e obter o modelo de regressão linear de exemplo: 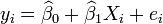$y_i = \ widehat {\ beta} _0 + \ widehat {\ beta} _1 x_i + e_i$ O termo 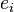$e_i$ é o resíduo, 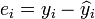$e_i = y_i - \ widehat {y} _i$ . Um método de estimativa é ordinário [Mínimos Quadrados]. Este método obtém estimativas de parâmetros que minimizam a soma do quadrado resíduos, SSE:

$SSE = \ sum_ {i = 1} ^ {} N ^ 2 e_i$

Minimização desta função resulta em um conjunto de equações normais, um conjunto de equações lineares nos parâmetros, os quais são resolvidos para se obter os estimadores de parâmetros, 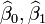$\ Widehat {\ beta} _0, \ widehat {\ beta} _1$ . Ver coeficientes de regressão para propriedades estatísticas desses estimadores.

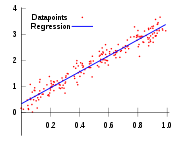
Ilustração de regressão linear em um conjunto de dados (pontos vermelhos).

No caso de regressão simples, as fórmulas para as estimativas de mínimos quadrados são

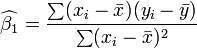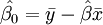
$\ Widehat {\ beta_1} = \ frac {\ sum (x_i- \ bar {x}) (y_i- \ bar {y})} {\ sum (x_i- \ bar {x}) ^ 2}$ e $\ Hat {\ beta_0} = \ bar {y} - \ hat {\ beta} \ bar {x}$

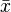onde $\ Bar {x}$ é a média (média) do 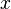$x$ e os valores 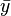$\ Bar {y}$ é a média da 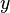$y$ valores. Ver lineares de mínimos quadrados (linha reta encaixe) para a derivação destas fórmulas e um exemplo numérico. Sob a hipótese de que o termo de erro população tem uma variância constante, a estimativa de variância que é dado por: 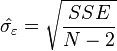$\ Hat {\ sigma _ {\ varepsilon}} = \ sqrt {\ frac {SSE} {N-2}}$ Isso é chamado de erro quadrático médio (RMSE) da regressão. O os erros padrão das estimativas dos parâmetros são dadas por

$\ Hat \ sigma _ {\ beta_0} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {N} + \ frac {\ bar {x} ^ 2} {\ sum (x_i- \ bar x) ^ 2}}$

$\ Hat \ sigma _ {\ beta_1} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {\ sum (x_i- \ bar x) ^ 2}}$

Sob a suposição adicional de que o termo de erro população é normalmente distribuída, o pesquisador pode usar esses erros estimados padrão para criar intervalos de confiança e testes de hipóteses realizar sobre os parâmetros populacionais.

Modelo de dados linear geral

No modelo de regressão múltipla mais geral, existem p variáveis independentes: 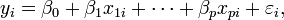$y_i = \ beta_0 + \ beta_1 x_ {} 1i + \ cdots + \ beta_p x_ {pi} + \ varepsilon_i,$ As estimativas de mínimos quadrados do parâmetro são obtidos por p equações normais. O resíduo pode ser escrito como

$e_i = y_i - \ hat \ beta_0 - \ hat \ beta_1 x_1 - \ cdots - \ hat \ beta_p x_p$

O equações normais são

$\ Sum_ {i = 1} ^ {N} \ sum_ {k = 1} ^ {p} X_ {ij} X_ {ik} \ hat \ beta_k = \ sum_ {i = 1} ^ {N} X_ {ij} y_i, \ j = 1, p \,$

Em notação matricial, as equações normais são escritos como

$\ Mathbf {\ left (X ^ TX \ right) \ hat \ boldsymbol \ beta = X ^ Ty}$

Para ver um exemplo numérico de regressão linear (exemplo)

Diagnósticos de regressão

Uma vez que um modelo de regressão foi construído, é importante para confirmar o qualidade de ajuste do modelo eo significância estatística dos parâmetros estimados. Cheques utilizados comumente de bondade de ajuste incluem o Análises do padrão de R-quadrado, resíduos e testes de hipóteses. A significância estatística é verificada por um F-teste do ajuste global, seguida por teste-t de parâmetros individuais.

Interpretações destes testes de diagnóstico descansar pesadamente sobre os pressupostos do modelo. Embora o exame dos residuais pode ser utilizado para invalidar um modelo, os resultados de um teste-t ou F-teste não têm significado se os pressupostos de modelagem estão satisfeitos.

O termo de erro pode não têm uma distribuição normal. Ver modelo linear generalizado.
A variável resposta pode ser não-contínuo. Para as variáveis binário (zero ou um), há o probit e modelo logit. O modelo probit multivariada torna possível estimar conjuntamente a relação entre diversas variáveis dependentes binárias e algumas variáveis independentes. Para variáveis categóricas com mais do que dois valores, há o logit multinomial. Para variáveis ordinais com mais do que dois valores, há o logit ordenado e modelos probit ordenado. Uma alternativa para tais procedimentos é a regressão linear baseado em correlações policóricas ou polyserial entre as variáveis categóricas. Tais procedimentos diferem nos pressupostos relativos à distribuição das variáveis na população. Se a variável é positivo, com valores baixos e representa a repetição da ocorrência de um evento, como a contagem de modelos A regressão de Poisson ou o modelo binomial negativo pode ser usado

Interpolação e extrapolação

Os modelos de regressão prever um valor de 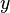$y$ os valores das variáveis indicadas conhecidos do 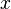$x$ variáveis. Se a previsão é para ser feito dentro da gama de valores da 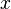$x$ variáveis utilizados para construir o modelo, isto é conhecido como interpolação . Predição fora do intervalo dos dados utilizados para construir o modelo é conhecido como extrapolação e é mais arriscado.

Regressão não linear

Quando a função de modelo não é linear nos parâmetros a soma dos quadrados deve ser minimizada através de um procedimento iterativo. Isso introduz muitas complicações que são resumidas em Diferenças entre linear e de mínimos quadrados não lineares

Outros métodos

Embora os parâmetros de um modelo de regressão são normalmente estimada usando o método dos mínimos quadrados, outros métodos que têm sido utilizados incluem:

Métodos Bayesianos
Minimização de desvios absolutos, levando a regressão quantílica
Regressão não paramétrica. Esta abordagem requer um grande número de observações, como os dados são utilizados para construir a estrutura do modelo, bem como estimar os parâmetros do modelo. Eles são geralmente computacionalmente intensiva.

Software

Todos os principais pacotes de software estatísticos executar os tipos mais comuns de análise de regressão corretamente e de forma amigável. A regressão linear simples pode ser feito em alguns aplicativos de planilha. Há uma série de programas de software que executam formas especializadas de regressão, e os peritos podem optar por escrever seu próprio código para usar linguagens de programação estatísticos ou software de análise numérica.

Retirado de " http://en.wikipedia.org/w/index.php?title=Regression_analysis&oldid=198424867 "

We provide Linux to the World