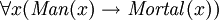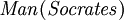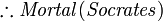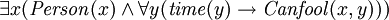La lógica de primer orden
Sabías ...
SOS Children, una organización benéfica educación , organizó esta selección. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.
La lógica de primer orden (FOL) es un oficial sistema deductivo utilizado por los matemáticos, filósofos, lingüistas e informáticos. Se conoce por muchos nombres, entre ellos: el cálculo de predicados de primer orden (FOPC), el cálculo de predicados inferior, el lenguaje de la lógica de primer orden o de la lógica de predicados. A diferencia de las lenguas naturales, tales como Inglés, FOL utiliza un totalmente inequívoca lenguaje formal interpretado por estructuras matemáticas. FOL es un sistema de deducción se extiende la lógica proposicional, permitiendo la cuantificación sobre los individuos de un determinado dominio (universo) del discurso. Por ejemplo, se puede afirmar en FOL "Todo individuo tiene la propiedad P".
Mientras ofertas lógica proposicional con proposiciones declarativas simples, lógica de primer orden, además, las cubiertas predicados y cuantificación. Tomemos, por ejemplo, las siguientes frases: "Sócrates es un hombre", "Platón es un hombre". En la lógica de proposiciones estos serán dos proposiciones no relacionados, denotadas por ejemplo p y q. En la lógica de primer orden, sin embargo, ambas oraciones estarían conectados por la misma propiedad: Hombre (x), donde el Hombre (x) significa que x es un hombre. Cuando x = Sócrates obtenemos la primera proposición, p, y cuando x = Platón obtenemos la segunda proposición, q. Dicha construcción permite una lógica mucho más potente cuando se introducen los cuantificadores, como "para cada x ...", por ejemplo, "para todo x, si el Hombre (x), entonces ...". Sin cuantificadores, cada argumento válido en FOL es válida en la lógica proposicional, y viceversa.
Una teoría de primer orden consiste en un conjunto de axiomas (generalmente finito o recursivamente enumerable) y las declaraciones deducible de ellos dada la relación de deducibilidad subyacente. Por lo general, lo que se entiende por 'teoría de primer orden "es un conjunto de axiomas junto con los de una (y sonido) axiomatización completa de la lógica de primer orden, cerrado bajo las reglas de FOL. (Cualquier sistema FOL dará lugar a la misma relación de deducibilidad abstracto, así que no tiene por qué tener un sistema axiomático fijo en mente.) Un lenguaje de primer orden tiene suficiente poder expresivo de formalizar dos teorías matemáticas importantes: ZFC la teoría de conjuntos y Aritmética de Peano. Un lenguaje de primer orden no puede, sin embargo, categóricamente expresar la noción de rendición a pesar de que es expresable en la teoría de primer orden ZFC bajo la interpretación pretendida del simbolismo de ZFC. Tales ideas se pueden expresar categóricamente con lógica de segundo orden.
¿Por qué es necesaria la lógica de primer orden?
La lógica proposicional no es adecuada para la formalización de argumentos válidos que se basan en la estructura interna de las proposiciones implicadas. Para ver esto, considere la válida argumento silogístico:
- Todos los hombres son mortales
- Sócrates es un hombre
- Por lo tanto, Sócrates es mortal
que tras la traducción a rendimientos lógica proposicional:
- La
- B
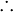 C
C
(Toma 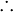 en el sentido de "por lo tanto").
en el sentido de "por lo tanto").
De acuerdo con la lógica proposicional, esta traducción no es válido: La lógica proposicional valida argumentos en función de su estructura, y nada en la estructura de este argumento traducido (C sigue de A y B, por arbitraria A, B, C) sugiere que es válido. Una traducción que preserve la validez intuitiva (y formal) del argumento debe tener en cuenta la estructura más profunda de las proposiciones, tales como las nociones esenciales de la predicación y la cuantificación. Ofertas de lógica proposicional sólo con validez verdad-funcional: cualquier asignación de valores de verdad a las variables del argumento debe hacer, ya sea la conclusión verdadera o al menos una de las premisas falsas. Claramente podemos (uniforme) asignamos valores de verdad a las variables del argumento anterior tal que A, B son ambas verdaderas pero C es falsa. De ahí que el argumento es verdad funcionalmente válido. Por otro lado, es imposible (uniformemente) asignar valores de verdad para el argumento "A sigue de (A y B)" de tal manera que (A y B) es verdadera (por lo tanto, A es verdadero y B es verdadero) y un falso .
Por el contrario, este argumento se puede traducir fácilmente en la lógica de primer orden:
(Donde " 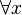 "Significa" para todo x ","
"Significa" para todo x ","  "Significa" implica ",
"Significa" implica ", 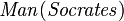 significa "Sócrates es un hombre", y
significa "Sócrates es un hombre", y 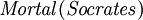 significa "Sócrates es mortal".) En la llanura Inglés, esto indica que
significa "Sócrates es mortal".) En la llanura Inglés, esto indica que
- para todo x, si x es un hombre entonces x es mortal
- Sócrates es un hombre
- por lo tanto, Sócrates es mortal
FOL también puede expresar la existencia de algo ( 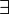 ), Así como predicados ("funciones" que son verdaderas o falsas) con más de un parámetro. Por ejemplo, "hay alguien que puede ser engañado cada vez que" se puede expresar como:
), Así como predicados ("funciones" que son verdaderas o falsas) con más de un parámetro. Por ejemplo, "hay alguien que puede ser engañado cada vez que" se puede expresar como:
Donde " 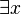 "Significa" existe (a) x ","
"Significa" existe (a) x "," 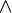 "Significa" y ", y
"Significa" y ", y 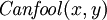 medios "(persona) x puede ser engañado (en el tiempo) y".
medios "(persona) x puede ser engañado (en el tiempo) y".
Definición lógica de primer orden
Un cálculo de predicados consiste en
- reglas de formación (es decir, definiciones recursivas para la formación fórmulas bien formadas).
- reglas de transformación (es decir, reglas de inferencia para derivar teoremas).
- axiomas o esquemas axioma (posiblemente infinito numerable).
Los axiomas son considerados aquí axiomas lógicos que forman parte del FOL clásica. Es importante señalar que FOL se puede formalizar en muchas formas equivalentes; no hay nada canónico sobre los axiomas y reglas de inferencia que figuran en este artículo. Hay un número infinito de formalizaciones equivalentes todas las cuales producen los mismos teoremas y no teoremas, y todos los cuales tienen igual derecho al título "FOL".
FOL se utiliza como "bloques de construcción" básico para muchas teorías matemáticas. FOL proporciona varias reglas incorporadas, tales como el axioma 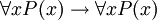 (Si P (x) es verdadera para cada x entonces P (x) es verdadera para cada x). Se añaden axiomas no-lógicos adicionales para producir teorías de primer orden específicas basadas en los axiomas de la FOL clásica; estas teorías construidas sobre FOL se llaman teorías de primer orden clásicas. Un ejemplo de una teoría clásica de primer orden es Aritmética de Peano, que se suma al axioma
(Si P (x) es verdadera para cada x entonces P (x) es verdadera para cada x). Se añaden axiomas no-lógicos adicionales para producir teorías de primer orden específicas basadas en los axiomas de la FOL clásica; estas teorías construidas sobre FOL se llaman teorías de primer orden clásicas. Un ejemplo de una teoría clásica de primer orden es Aritmética de Peano, que se suma al axioma 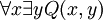 (Es decir, para cada x existe y tal que y = x + 1, donde Q (x, y) se interpreta como "y = x + 1"). Este axioma adicional es un axioma no-lógico; no es parte de FOL, pero en su lugar es un axioma de la teoría (un axioma de la aritmética en vez de la lógica). Axiomas de la última clase son también llamados axiomas de teorías de primer orden. Los axiomas de teorías de primer orden no se consideran verdades de la lógica en sí misma, sino como verdades de la teoría particular que por lo general ha asociado a él una interpretación pretendida de sus símbolos no lógicos. (Ver una idea análoga en lógica frente símbolos no lógico.) Por lo tanto, el axioma sobre Q (x, y) es cierto sólo con la interpretación de la relación Q (x, y) como "y = x + 1", y sólo en la teoría de la Aritmética de Peano. FOL clásica no tiene asociada con ella una interpretación pretendida de su vocabulario no lógico (excepto posiblemente un símbolo que denota la identidad, dependiendo de si uno considera un símbolo como lógico). Clásica set-teoría es otro ejemplo de una teoría de primer orden (una teoría construida sobre FOL).
(Es decir, para cada x existe y tal que y = x + 1, donde Q (x, y) se interpreta como "y = x + 1"). Este axioma adicional es un axioma no-lógico; no es parte de FOL, pero en su lugar es un axioma de la teoría (un axioma de la aritmética en vez de la lógica). Axiomas de la última clase son también llamados axiomas de teorías de primer orden. Los axiomas de teorías de primer orden no se consideran verdades de la lógica en sí misma, sino como verdades de la teoría particular que por lo general ha asociado a él una interpretación pretendida de sus símbolos no lógicos. (Ver una idea análoga en lógica frente símbolos no lógico.) Por lo tanto, el axioma sobre Q (x, y) es cierto sólo con la interpretación de la relación Q (x, y) como "y = x + 1", y sólo en la teoría de la Aritmética de Peano. FOL clásica no tiene asociada con ella una interpretación pretendida de su vocabulario no lógico (excepto posiblemente un símbolo que denota la identidad, dependiendo de si uno considera un símbolo como lógico). Clásica set-teoría es otro ejemplo de una teoría de primer orden (una teoría construida sobre FOL).
Vocabulario
Antes de configurar las reglas de formación, hay que describir el "vocabulario", que se compone de
- Un conjunto de variables determinantes (o relaciones) cada uno con un poco de valencia (o aridad, varios de sus argumentos) ≥1, que a menudo se designan por letras mayúsculas P, Q, R, ....
- Por ejemplo, P (x) es una las variables determinantes de valencia 1. Puede significar "x es un hombre", por ejemplo.
- Q (x, y) es una las variables determinantes de valencia 2. Puede significar "x es mayor que y" en aritmética o "x es el padre de y", por ejemplo.
- Es posible permitir que las relaciones de valencia 0; éstos podrían ser considerados como variables proposicionales. Por ejemplo, P, que puede presentarse a cualquier declaración.
- Mediante el uso de funciones (véase más adelante), es posible prescindir de todas las variables determinantes con valencia mayor que uno. Por ejemplo, "x> y" (un predicado de valencia 2, del tipo Q (x, y)) se puede sustituir por un predicado de valencia 1 sobre la par ordenado (x, y).
- Un conjunto de constantes, a menudo indicado por letras minúsculas al comienzo del alfabeto a, b, c, ....
- Ejemplos: una puede presentarse a Sócrates. En aritmética , puede presentarse a 0. En la teoría de conjuntos , una constante de este tipo puede presentarse a la conjunto vacío.
- Un conjunto de funciones, cada uno de algunos de valencia ≥ 1, que a menudo se denota con letras minúsculas f, g, h, ....
- Ejemplos: f (x) puede significar "el padre de x". En aritmética , puede significar "-x". En la teoría de conjuntos , puede significar "la conjunto potencia de x ". En aritmética , f (x, y) puede significar "x + y". En la teoría de conjuntos , puede significar "la unión de xey".
- Una constante es realmente una función de la valencia 0. Sin embargo, es tradicional el uso del término "función" sólo para funciones de valencia al menos 1.
- Uno puede, en principio, abstenernos por completo de funciones de aridad> 2 y predicados de aridad> 1 si hay un símbolo de la función de aridad 2 representa un par ordenado (o símbolos de predicado de aridad 2 que representan las relaciones de proyección de un par ordenado). La pareja o proyecciones necesitan satisfacer los axiomas naturales.
- Uno puede, en principio, prescindir por completo de funciones y constantes. Por ejemplo, en lugar de utilizar una constante 0 se puede utilizar un predicado 0 (x) (interpretado como "x = 0"), y reemplazar cada predicado tales como P (0, y) con
 x 0 (x)
x 0 (x)  P (x, y). Una función como f (x1, x2 ...) de manera similar será reemplazado por un predicado F (x1, x2 ..., y) (interpretado como "y = f (x1, x2 ...)").
P (x, y). Una función como f (x1, x2 ...) de manera similar será reemplazado por un predicado F (x1, x2 ..., y) (interpretado como "y = f (x1, x2 ...)").
- Un conjunto infinito de variables, a menudo indicado por letras minúsculas al final del alfabeto x, y, z, ....
- Símbolos que denotan operadores lógicos (o conectores):
 ( no es lógico),
( no es lógico),  ( condicional lógico).
( condicional lógico).  (Φ
(Φ 
 ψ) es lógicamente equivalente a φ
ψ) es lógicamente equivalente a φ 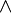 ψ ( lógico y). φ
ψ ( lógico y). φ 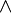 ψ puede ser visto como una forma rápida para esto. Alternativamente, se puede añadir el
ψ puede ser visto como una forma rápida para esto. Alternativamente, se puede añadir el 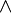 símbolo como un operador lógico al vocabulario y axiomas apropiados.
símbolo como un operador lógico al vocabulario y axiomas apropiados.  φ
φ  ψ es lógicamente equivalente a φ
ψ es lógicamente equivalente a φ  ψ ( lógico o). φ
ψ ( lógico o). φ  ψ puede ser visto como una forma rápida para esto. Alternativamente, se puede añadir el
ψ puede ser visto como una forma rápida para esto. Alternativamente, se puede añadir el  símbolo como un operador lógico al vocabulario y axiomas apropiados.
símbolo como un operador lógico al vocabulario y axiomas apropiados. - Del mismo modo, (φ
 ψ)
ψ) 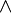 (Ψ
(Ψ  φ) es lógicamente equivalente a φ
φ) es lógicamente equivalente a φ 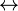 ψ ( bicondicional lógico), y uno puede utilizar este último como un atajo para esto, o, alternativamente, añadir este al vocabulario y añadir axiomas apropiados. A veces φ
ψ ( bicondicional lógico), y uno puede utilizar este último como un atajo para esto, o, alternativamente, añadir este al vocabulario y añadir axiomas apropiados. A veces φ 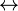 ψ se escribe como φ
ψ se escribe como φ  ψ.
ψ.
- Símbolos que denotan cuantificadores:
 ( cuantificación universal, lea típicamente como "para todos").
( cuantificación universal, lea típicamente como "para todos"). 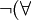 x
x  φ) es lógicamente equivalente a
φ) es lógicamente equivalente a 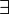 x φ ( cuantificación existencial, lea típicamente como "existe"). Este último puede ser utilizado ya sea como una abreviatura para este, o añadido al vocabulario junto con axiomas apropiados.
x φ ( cuantificación existencial, lea típicamente como "existe"). Este último puede ser utilizado ya sea como una abreviatura para este, o añadido al vocabulario junto con axiomas apropiados.
- La izquierda y la derecha paréntesis.
- Hay muchas convenciones diferentes sobre dónde poner entre paréntesis; por ejemplo, uno podría escribir
 x o (
x o (  x). A veces uno utiliza dos puntos o puntos en lugar de paréntesis para hacer fórmulas ambiguas. Una convención interesante pero bastante inusual es " Notación polaca ", donde se omite todos los paréntesis, y escribe
x). A veces uno utiliza dos puntos o puntos en lugar de paréntesis para hacer fórmulas ambiguas. Una convención interesante pero bastante inusual es " Notación polaca ", donde se omite todos los paréntesis, y escribe  ,
,  , Y así sucesivamente delante de sus argumentos en vez de entre ellos. Notación polaca es compacto y elegante, pero rara porque es difícil para los seres humanos lo lean.
, Y así sucesivamente delante de sus argumentos en vez de entre ellos. Notación polaca es compacto y elegante, pero rara porque es difícil para los seres humanos lo lean.
- Hay muchas convenciones diferentes sobre dónde poner entre paréntesis; por ejemplo, uno podría escribir
- Un símbolo de la identidad o la igualdad = a veces, pero no siempre se incluye en el vocabulario.
- Si la igualdad se considera que es una parte de la lógica de primer orden, entonces el símbolo de la igualdad comporta sintácticamente como un predicado binario. Este caso se llama a veces lógica de primer orden con igualdad.
Hay varias variaciones menores adicionales listados a continuación:
- El conjunto de símbolos primitivos (operadores y cuantificadores) varía a menudo. Es posible incluir otros operadores como primitivos, como
 (FIB),
(FIB),  (Y) y
(Y) y  (O), la verdad constantes T para la "verdadera" y F para "false" (estos son los operadores de valencia 0), y / o el Sheffer carrera (P | Q, alias NAND). El número mínimo de símbolos primitivos necesarios es uno, pero si nos limitamos a los operadores mencionados anteriormente, necesitamos tres, como antes.
(O), la verdad constantes T para la "verdadera" y F para "false" (estos son los operadores de valencia 0), y / o el Sheffer carrera (P | Q, alias NAND). El número mínimo de símbolos primitivos necesarios es uno, pero si nos limitamos a los operadores mencionados anteriormente, necesitamos tres, como antes. - Algunos libros y papeles utilizan la notación φ
 ψ para φ
ψ para φ  ψ. Esto es especialmente común en la teoría de la prueba en caso
ψ. Esto es especialmente común en la teoría de la prueba en caso  se confunde fácilmente con la flecha consecuente. Se ve también ~ φ para
se confunde fácilmente con la flecha consecuente. Se ve también ~ φ para  φ, φ y ψ para φ
φ, φ y ψ para φ 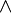 ψ, y una gran cantidad de anotaciones para cuantificadores; por ejemplo,
ψ, y una gran cantidad de anotaciones para cuantificadores; por ejemplo,  x φ se puede escribir como (x) φ. Esta última notación es común en los textos sobre teoría de la repetición.
x φ se puede escribir como (x) φ. Esta última notación es común en los textos sobre teoría de la repetición. - A menudo es más fácil en la práctica de utilizar una notación más simple que soporta operadores infijos y omite paréntesis innecesarios. Así, si P es una relación de valencia 2, escribimos a menudo "un P b" en lugar de "P ab"; por ejemplo, escribimos 1 <2 en lugar de <(1 2). Del mismo modo, si f es una función de la valencia 2, a veces nos escribimos "afb" en lugar de "f (ab)"; por ejemplo, escribimos 1 + 2 en lugar de + (1 2). Por convención, los operadores infijos tienden a utilizar nombres de funciones no alfabéticos. También es común a omitir algunos paréntesis, si esto no conduce a la ambigüedad (que conduce a la definición de una prioridad).
- A veces es útil decir que "P (x) tiene exactamente un x", que se puede expresar como
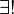 x P (x). Esta notación se puede tomar para abreviar una fórmula como
x P (x). Esta notación se puede tomar para abreviar una fórmula como 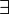 x (P (x)
x (P (x) 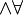 y (P (y)
y (P (y)  (X = y))).
(X = y))).
Los programas de ordenador que aceptan representaciones lógicas de primer orden serán normalmente aceptar al menos estos cuantificadores y operadores (aunque pueden usar diferentes símbolos para representarlos):  (Para todos),
(Para todos), 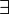 (Existe),
(Existe),  (No),
(No), 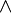 (Y),
(Y),  (O),
(O),  (Implica), y
(Implica), y 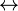 (Si y solo si). La exclusivo u operador "xor" también es común.
(Si y solo si). La exclusivo u operador "xor" también es común.
Los conjuntos de constantes, funciones y relaciones suelen ser considerados para formar una lengua, mientras que las variables, operadores lógicos, y cuantificadores se consideran generalmente pertenecen a la lógica. Por ejemplo, el lenguaje de la teoría de grupos consiste en una constante (el elemento de identidad), una función de la valencia 1 (la inversa) una función de la valencia 2 (el producto), y una relación de valencia 2 (igualdad), lo que sería omitido por autores que incluyen la igualdad en la lógica subyacente.
Reglas de formación
Las reglas de formación definen los términos y fórmulas de la lógica de primer orden. Cuando los términos y fórmulas se representan como cadenas de símbolos, estas reglas se pueden utilizar para escribir una gramática formal para los términos y fórmulas. El concepto de variable libre se utiliza para definir las frases como un subconjunto de las fórmulas.
Condiciones
El conjunto de términos se definen recursivamente por las siguientes reglas:
- Cualquier constante es un término.
- Cualquier variable es un término.
- Cualquier expresión f (t 1, ..., t n) de n ≥ 1 argumentos (donde cada argumento t i es un término y F es un símbolo de la función de la valencia n) es un término.
- Cláusula de cierre: Nada más es un término. Por ejemplo, los predicados no son términos.
Fórmulas
El conjunto de fórmulas bien formadas (generalmente llamados s WFF o simplemente fórmulas) es recursiva definidos por las siguientes reglas:
- Predicados simples y complejas Si P es una relación de valencia n ≥ 1 y el un i son términos entonces P (a, ..., a n 1) está bien formada. Si la igualdad se considera parte de la lógica, entonces (a 1 = a 2) está bien formado. Todas estas fórmulas se dice que son atómica.
- Cláusula inductiva I: Si φ es una wff, a continuación,
 φ es un wff.
φ es un wff. - Cláusula inductiva II: Si φ y ψ son s WFF, entonces (φ
 ψ) es un wff.
ψ) es un wff. - Cláusula inductiva III: Si φ es una wff yx es una variable, luego
 x φ es un wff.
x φ es un wff. - Cierre Cláusula: Nada más es un wff.
Por ejemplo,  x
x  y (P (f (x))
y (P (f (x)) 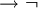 (P (x)
(P (x)  Q (f (y), x, z))) es una fórmula bien formada, si f es una función de la valencia 1, P un predicado de valencia 1 y Q un predicado de valencia 3.
Q (f (y), x, z))) es una fórmula bien formada, si f es una función de la valencia 1, P un predicado de valencia 1 y Q un predicado de valencia 3.  xx
xx  no es una fórmula bien formada.
no es una fórmula bien formada.
En Informática terminología, una fórmula implementa un tipo "boolean" incorporado, mientras que un término implementa todos los otros tipos.
Variables libres y combinados
- Fórmulas atómicas Si φ es una fórmula atómica entonces x es libre en φ si y sólo si x se produce en φ.
- Inductivo Cláusula I: x está libre en
 φ si y sólo si x está libre en φ.
φ si y sólo si x está libre en φ. - Cláusula inductiva II: x está libre en (φ
 ψ) si y sólo si x está libre en φ y no se produce en ψ, o x es libre en ψ y no se produce en φ, o x es libre en tanto φ y ψ.
ψ) si y sólo si x está libre en φ y no se produce en ψ, o x es libre en ψ y no se produce en φ, o x es libre en tanto φ y ψ. - Cláusula inductiva III: x está libre en
 y φ si y sólo si x está libre en φ y x es un símbolo diferente de y.
y φ si y sólo si x está libre en φ y x es un símbolo diferente de y. - Cierre Cláusula: x es encuadernado en φ si y sólo si x se produce en φ y x no es libre en φ.
- Por ejemplo, en
 x
x  y (P (x)
y (P (x)  Q (x, f (x), z) de variables), X e Y están unidos, z es una variable libre, y w es ni porque no se produce en la fórmula.
Q (x, f (x), z) de variables), X e Y están unidos, z es una variable libre, y w es ni porque no se produce en la fórmula.
Ejemplo
En matemáticas el lenguaje de los grupos abelianos ordenado tiene una constante 0, una función unaria -, una función binaria +, y una relación binaria ≤. Por lo tanto:
- 0, x, y son términos atómicos
- + (X, y), + (x, + (y, - (z))) son términos, por lo general escribe como x + y, x + y - z
- = (+ (X, y), 0), ≤ (+ (x, + (y, - (z))), + (x, y)) son fórmulas atómicas, generalmente escrito como x + y = 0, x + y - z ≤ x + y,
- (
 x
x  y ≤ (+ (x, y), z))
y ≤ (+ (x, y), z))  (
(  x = (+ (x, y), 0)) es una fórmula, generalmente escrito como (
x = (+ (x, y), 0)) es una fórmula, generalmente escrito como (  x
x  y z y ≤ x +)
y z y ≤ x +)  (
(  x x + y = 0).
x x + y = 0).
Sustitución
Si t es un término y φ (x) es una fórmula que contiene posiblemente x como una variable libre, entonces φ (t) se define como el resultado de reemplazar todas las instancias gratuitas de x por t, siempre que ninguna variable libre de t se convierte en obligado en este proceso. Si alguna variable libre de t llega a unirse, a continuación, para sustituir t por x, primero es necesario cambiar los nombres de las variables ligadas de φ a algo distinto de las variables libres de t.
Para ver por qué esta condición es necesario, considerar la fórmula φ (x) dada por  y y x ≤ ("x es máxima"). Si t es un término sin y como una variable libre, entonces φ (t) sólo significa t es máxima. Sin embargo, si t es y la fórmula φ (y) es
y y x ≤ ("x es máxima"). Si t es un término sin y como una variable libre, entonces φ (t) sólo significa t es máxima. Sin embargo, si t es y la fórmula φ (y) es  s s ≤ y que no dice que y es máxima. El problema es que la variable y libre de t (= y) quedó obligado cuando sustituimos y por x en φ (x). Así que para formar φ (y) debemos primero cambiar la variable ligada a de φ a otra cosa, decir z, de modo que φ (y) es entonces
s s ≤ y que no dice que y es máxima. El problema es que la variable y libre de t (= y) quedó obligado cuando sustituimos y por x en φ (x). Así que para formar φ (y) debemos primero cambiar la variable ligada a de φ a otra cosa, decir z, de modo que φ (y) es entonces  z ≤ z y. Olvidando esta condición es una causa notoria de errores.
z ≤ z y. Olvidando esta condición es una causa notoria de errores.
Las reglas de inferencia
Una regla de inferencia es una función de los conjuntos de fórmulas (bien formados), llamado locales, a conjuntos de fórmulas llamados conclusiones. En sistemas deductivos más conocidos, reglas de inferencia toman un conjunto de fórmulas para una sola conclusión. (Tenga en cuenta que esto es cierto incluso en el caso de la mayoría cálculos consecuente.)
Las reglas de inferencia se utilizan para demostrar teoremas , que son fórmulas demostrables en o miembros de una teoría. Si el instalaciones de una regla de inferencia son teoremas, entonces su conclusión es un teorema también. En otras palabras, se utilizan reglas de inferencia para generar "nuevos" teoremas de los "viejos" - están theoremhood preservando. Los sistemas para la generación de teorías a menudo se llaman cálculos subyacentes. Estos se describen en una sección de abajo.
Una regla de inferencia importante, modus ponens, establece que si φ y φ  ψ son los dos teoremas, entonces ψ es un teorema. Esto se puede escribir de la siguiente manera;
ψ son los dos teoremas, entonces ψ es un teorema. Esto se puede escribir de la siguiente manera;
- si
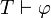 y
y 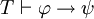 , A continuación,
, A continuación, 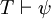
donde 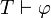 indica
indica  es demostrable en la teoría T. Hay sistemas deductivos (conocido como De estilo Hilbert sistemas deductivos) en el que el modus ponens es la única regla de inferencia; en tales sistemas, la falta de otras reglas de inferencia se compensa con una gran cantidad de esquemas de axiomas lógicos.
es demostrable en la teoría T. Hay sistemas deductivos (conocido como De estilo Hilbert sistemas deductivos) en el que el modus ponens es la única regla de inferencia; en tales sistemas, la falta de otras reglas de inferencia se compensa con una gran cantidad de esquemas de axiomas lógicos.
Una segunda regla de inferencia es importante Generalización universal. Se puede afirmar que
- si
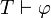 , A continuación,
, A continuación, 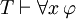
Que dice: si φ es un teorema, entonces "para cada x, φ" es un teorema también. El esquema de aspecto similar 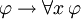 no tiene fundamento, en general, a pesar de que sin embargo tiene casos válidos, como cuando x no ocurre libre en φ (ver Generalización (lógica)).
no tiene fundamento, en general, a pesar de que sin embargo tiene casos válidos, como cuando x no ocurre libre en φ (ver Generalización (lógica)).
Axiomas
Aquí sigue una descripción de los axiomas de la lógica de primer orden. Como se explicó anteriormente, una teoría de primer orden dado tiene más, axiomas no-lógicos. Los siguientes axiomas lógicos caracterizan un cálculo de predicados por ejemplo de la lógica de primer orden de este artículo.
Para cualquier teoría, es de interés saber si el conjunto de axiomas puede ser generado por un algoritmo, o si hay un algoritmo que determina si una fórmula bien formada es un axioma.
Si hay un algoritmo para generar todos los axiomas, entonces se dice que el conjunto de axiomas para ser recursivamente enumerable.
Si hay un algoritmo que determina después de un número finito de pasos si una fórmula es un axioma o no, entonces se dice que el conjunto de axiomas para ser recursivo o decidible. En ese caso, también se puede construir un algoritmo para generar todos los axiomas: este algoritmo se basa simplemente todas las fórmulas posibles, uno por uno (con la creciente longitud), y para cada fórmula el algoritmo determina si se trata de un axioma.
Axiomas de la lógica de primer orden son siempre decidible. Sin embargo, en una teoría de primer orden axiomas no-lógicos no son necesariamente así.
Axiomas cuantificador
Axiomas cuantificador cambian de acuerdo a cómo se define el vocabulario, cómo funciona el procedimiento de sustitución, ¿cuáles son las reglas de formación y las que se utilizan reglas de inferencia. Aquí sigue un ejemplo específico de estos axiomas
- PRED-1:
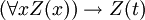
- PRED-2:
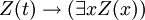
- PRED-3:
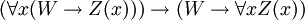
- PRED-4:
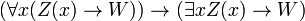
Estas son en realidad esquemas axioma: la expresión W representa cualquier wff en la que x no es libre, y la expresión Z (x) representa cualquier wff con el convenio adicional que Z (t) representa el resultado de la sustitución del término t por x en Z (x). Así, esta es una conjunto recursivo de axiomas.
Otro axioma,  , Por Z en la que no se produce x, se añade a veces.
, Por Z en la que no se produce x, se añade a veces.
Igualdad y sus axiomas
Hay varias convenciones diferentes para el uso de la igualdad (o identidad) en la lógica de primer orden. Esta sección resume los principales. Las diversas convenciones todos dan esencialmente los mismos resultados con la misma cantidad de trabajo, y se diferencian principalmente en la terminología.
- La convención más común para la igualdad es incluir el símbolo de la igualdad como un símbolo lógico primitivo, y añadir los axiomas de igualdad a los axiomas de la lógica de primer orden. Los axiomas de igualdad son
- x = x
- x = y → f (..., x, ...) = f (..., y, ...) para cualquier función f
- x = y → (P (..., x, ...) → P (..., y, ...)) para cualquier relación P (incluida la propia relación de igualdad)
- Estos son, también, esquemas axioma: definen un algoritmo que decide si una fórmula dada es un axioma. Así, esta es una conjunto recursivo de axiomas.
- La próxima convención más común es incluir el símbolo de la igualdad como una de las relaciones de una teoría, y añadir los axiomas de igualdad a los axiomas de la teoría. En la práctica esto es casi indistinguible de la convención anterior, salvo en el caso inusual de teorías que no tienen noción de igualdad. Los axiomas son los mismos, y la única diferencia es si uno llama a algunos de ellos axiomas lógicos o axiomas de la teoría.
- En las teorías que no tienen funciones y un número finito de relaciones, es posible definir la igualdad en términos de las relaciones, mediante la definición de los dos términos s y t ser iguales si ninguna relación no se ha modificado cambiando s en t en cualquier argumento.
- Por ejemplo, en la teoría de conjuntos con una relación
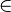 , Podemos definir s = t ser una abreviatura de
, Podemos definir s = t ser una abreviatura de  x (s
x (s 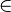 x
x 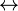 t
t 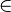 x)
x) 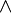
 x (x
x (x  s
s  x
x  t). Esta definición de la igualdad entonces satisface automáticamente los axiomas de igualdad.
t). Esta definición de la igualdad entonces satisface automáticamente los axiomas de igualdad. - Por otra parte, si uno lo hace utilizar el símbolo de igualdad como una relación de la teoría o de la lógica, entonces habría que añadir axiomas. En el ejemplo anterior, habría que añadir el axioma
 s
s  t (
t (  x (x
x (x  s
s 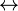 x
x 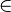 t))
t))  s = t.
s = t.
- Por ejemplo, en la teoría de conjuntos con una relación
- En algunas teorías es posible dar definiciones ad hoc de la igualdad. Por ejemplo, en una teoría de órdenes parciales con una relación ≤ podríamos definir s = t ser una abreviatura para s ≤ t
 t ≤ s.
t ≤ s.
El cálculo de predicados
El cálculo de predicados es una extensión apropiada del cálculo proposicional que define qué enunciados de la lógica de primer orden son demostrables. Muchos (pero no todos) teorías matemáticas se pueden formular en el cálculo de predicados. Si el cálculo proposicional se define con un conjunto adecuado de axiomas y la única regla de inferencia modus ponens (esto se puede hacer de muchas maneras), entonces el cálculo de predicados pueden ser definidos por anexar al cálculo proposicional varios axiomas y la regla de inferencia llamada "generalización universal". Como axiomas para el cálculo de predicados tomamos:
- Todos los tautologías del cálculo de proposiciones, tomadas esquemáticamente de manera que se permite la sustitución uniforme de una carta esquemática por una fórmula.
- Los axiomas cuantificador, dado anteriormente.
- Los axiomas anteriores para la igualdad, si la igualdad es considerado como un concepto lógico.
Una frase se define para ser demostrable en la lógica de primer orden si se puede derivar de los axiomas del cálculo de predicados, aplicando repetidamente las reglas de inferencia "modus ponens" y "generalización universal". En otras palabras:
- Un axioma del cálculo de predicados es demostrable en la lógica de primer orden, por definición.
- Si el instalaciones de una regla de inferencia son demostrables en lógica de primer orden, también lo es su conclusión.
Si tenemos una teoría T (un conjunto de estados, llamados axiomas, en algún idioma) y luego un φ frase se define a ser demostrable en la teoría T si
es demostrable en la lógica de primer orden, para algún conjunto finito de axiomas  de la teoría T. En otras palabras, si uno puede probar en la lógica de primer orden que φ se sigue de los axiomas de T. Esto también significa, que sustituimos el procedimiento anterior para encontrar frases demostrables, por el siguiente:
de la teoría T. En otras palabras, si uno puede probar en la lógica de primer orden que φ se sigue de los axiomas de T. Esto también significa, que sustituimos el procedimiento anterior para encontrar frases demostrables, por el siguiente:
- Un axioma de T es demostrable en T.
- Un axioma del cálculo de predicados es demostrable en T.
- Si el instalaciones de una regla de inferencia son demostrables en T, entonces también lo es su conclusión.
Un problema evidente con esta definición de demostrabilidad es que parece bastante ad hoc: hemos tomado alguna colección aparentemente aleatoria de axiomas y reglas de inferencia, y no está claro que no hemos perdido accidentalmente algún axioma vital o regla. Exhaustividad teorema de Gödel nos asegura que esto no es realmente un problema: cualquier declaración verdadera en todos los modelos (semánticamente verdaderos) es demostrable en la lógica de primer orden (sintácticamente cierto). En particular, cualquier definición razonable de "demostrable" en lógica de primer orden debe ser equivalente a la anterior (aunque es posible que las longitudes de pruebas difieran mucho de las diferentes definiciones de demostrabilidad).
Hay muchas maneras diferentes (pero equivalentes) para definir demostrabilidad. La definición anterior es típico de un cálculo "estilo Hilbert", que tiene muchos axiomas pero muy pocas reglas de inferencia. Por el contrario, una "Estilo Gentzen" cálculo de predicados tiene pocos axiomas pero muchas reglas de inferencia.
Identidades demostrables
Las siguientes frases se pueden llamar "identidades", porque el término de enlace principal en cada uno es la bicondicional. Todos ellos son demostrables en FOL, y son útiles en la manipulación de los cuantificadores:
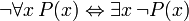
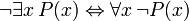
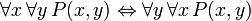
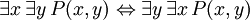
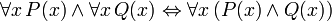
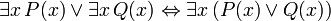
 (Donde
(Donde 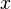 no debe ocurrir en libre
no debe ocurrir en libre 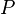 )
)  (Donde
(Donde 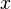 no debe ocurrir en libre
no debe ocurrir en libre 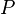 )
)
Reglas de inferencia demostrables
El conectivo principal en las siguientes frases, también demostrable en FOL, es la condicional. Estas frases pueden ser vistos como la justificación de las reglas de inferencia, además de modus ponens y generalización universal, examinadas anteriormente y se asumieron válida:
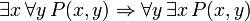
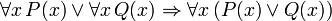
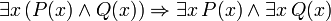
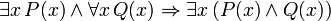
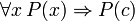 (Si c es una variable, entonces no debe ser cuantificada previamente en P (x))
(Si c es una variable, entonces no debe ser cuantificada previamente en P (x)) 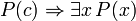 (Debe haber ningún caso libre de x en P (c))
(Debe haber ningún caso libre de x en P (c))
Teoremas metalógicos de la lógica de primer orden
Algunos teoremas metalógicos importantes se enumeran a continuación en forma de viñetas. Lo que quieren decir es que más o menos una oración es válida si y sólo si es demostrable. Además, se puede construir un algoritmo que funciona de la siguiente manera: si una frase es demostrable, el algoritmo nos dicen que en una cantidad finita pero desconocido de tiempo. Si una frase es indemostrable, el algoritmo se ejecutará siempre, y no vamos a saber si la frase es indemostrable o demostrable y el algoritmo todavía no nos lo ha dicho. Tal algoritmo se llama semidecidable o recursivamente enumerable.
Uno puede construir un algoritmo que determinará en número finito de pasos si una oración es demostrable (un algoritmo decidible) sólo para clases simples de la lógica de primer orden.
- El problema de decisión para la validez es recursivamente enumerable; En otras palabras, hay una Máquina de Turing que cuando se les da ninguna pena como entrada, se detendrá si y sólo si la sentencia es válida (cierto en todos los modelos).
- Como Espectáculos teorema de completitud de Gödel, para cualquier fórmula válida P, P es demostrable. A la inversa, suponiendo que la consistencia de la lógica, cualquier fórmula demostrable es válido.
- La máquina de Turing puede ser uno que genera todas las fórmulas demostrables de la siguiente manera: para un finito o recursivamente enumerable conjunto de axiomas, una máquina de este tipo puede ser uno que genera un axioma, a continuación, genera una nueva fórmula demostrable mediante la aplicación de axiomas y reglas de inferencia ya generados, a continuación, generar otro axioma, y así sucesivamente. Dada una frase como entrada, la máquina de Turing simplemente seguir y genera todas las fórmulas demostrables uno por uno, y se detendrá si genera la sentencia.
- A diferencia de la la lógica proposicional, lógica de primer orden es indecidible, siempre que el lenguaje tiene al menos un predicado de valencia, al menos, 2 que no sea la igualdad. Esto significa que no hay procedimiento de decisión que determina correctamente si una fórmula arbitraria es válido. Debido a que existe una máquina de Turing como se ha descrito anteriormente, la indecidibilidad está relacionada con la insolubilidad de la Problema de la parada: no hay algoritmo que determina después de un número finito de pasos si la máquina de Turing jamás alto por una sentencia dada como su entrada, por lo tanto, si la sentencia es demostrable. Este resultado se estableció de forma independiente por Iglesia y Turing .
- La lógica de predicados Monádica (es decir, la lógica de predicados con sólo predicados de un argumento y no hay funciones) es decidible.
- La Clase Bernays-Schönfinkel de fórmulas de primer orden también es decidible.
La traducción de lenguaje natural para la lógica de primer orden
Conceptos expresados en lenguaje natural deben ser "traducidos" a la lógica de primer orden (FOL) antes de FOL puede utilizarse para abordarlos, y hay una serie de peligros potenciales en esta traducción. En FOL, 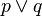 significa "p, q o, o ambos", es decir, que es inclusivo. En Inglés, la palabra "o" es a veces incluido (por ejemplo, "crema o azúcar?"), Pero a veces es exclusiva (por ejemplo, "el café o té?" Se destina generalmente para significar uno o el otro, pero no ambos). Del mismo modo, la palabra Inglés "algo" puede significar "al menos uno, posiblemente todos", pero otras veces puede significar "no todos, posiblemente ninguno". La palabra Inglés "y" a veces se debe traducir como "o" (por ejemplo, "los hombres y las mujeres pueden aplicar").
significa "p, q o, o ambos", es decir, que es inclusivo. En Inglés, la palabra "o" es a veces incluido (por ejemplo, "crema o azúcar?"), Pero a veces es exclusiva (por ejemplo, "el café o té?" Se destina generalmente para significar uno o el otro, pero no ambos). Del mismo modo, la palabra Inglés "algo" puede significar "al menos uno, posiblemente todos", pero otras veces puede significar "no todos, posiblemente ninguno". La palabra Inglés "y" a veces se debe traducir como "o" (por ejemplo, "los hombres y las mujeres pueden aplicar").
Las limitaciones de la lógica de primer orden
Todas las notaciones matemáticas tienen sus puntos fuertes y débiles;aquí están algunos de esos problemas con la lógica de primer orden.
Dificultad que representa if-then-else
Por extraño que parezca, FOL con igualdad (tal como se define normalmente) no incluye ni permite la definición de un if-then-else predicado o función si (c, a, b), donde "c" es una condición expresa como una fórmula, mientras que una y b son o bien ambos términos o ambas fórmulas, y su resultado sería "a" si c es verdadera, y "b" si es falso. El problema es que en FOL, ambos predicados y funciones sólo pueden aceptar los términos ("no-booleanos") como parámetros, pero la representación "evidente" de la enfermedad es una fórmula ("booleano"). Esto es lamentable, ya que muchas funciones matemáticas se expresan convenientemente en términos de si-entonces-más, y si-entonces-else es fundamental para la descripción de la mayoría de los programas de ordenador.
Matemáticamente, es posible volver a definir un conjunto completo de nuevas funciones que responden a los operadores de fórmula, pero esto es bastante torpe. Un predicado si (c, a, b) se puede expresar en FOL si reescrito como 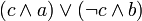 , pero esto es torpe si la condición c es compleja. Muchos se extienden FOL para agregar un predicado caso especial denominada "si (condición, a, b)" (donde a y b son fórmulas) y / o la función "ite (condición, a, b)" (donde ayb son términos ), ambos de los cuales acepta una fórmula como la condición, y es igual a "a" si la condición es verdadera y "b" si es falso. Estas extensiones hacen FOL más fácil de usar para algunos problemas, y hacer algunos tipos de automática más fácil teorema de probar. Otros extienden FOL más por lo que las funciones y predicados pueden aceptar ambos términos y fórmulas en cualquier posición.
, pero esto es torpe si la condición c es compleja. Muchos se extienden FOL para agregar un predicado caso especial denominada "si (condición, a, b)" (donde a y b son fórmulas) y / o la función "ite (condición, a, b)" (donde ayb son términos ), ambos de los cuales acepta una fórmula como la condición, y es igual a "a" si la condición es verdadera y "b" si es falso. Estas extensiones hacen FOL más fácil de usar para algunos problemas, y hacer algunos tipos de automática más fácil teorema de probar. Otros extienden FOL más por lo que las funciones y predicados pueden aceptar ambos términos y fórmulas en cualquier posición.
Typing (Sorts)
FOL no incluye tipos (ordena) en la misma notación, aparte de la diferencia entre las fórmulas ("booleanos") y los términos ("no-booleanos"). Algunos argumentan que esta falta de tipos es una gran ventaja, pero muchos otros se encuentran ventajas en la definición y el uso de tipos (clases), como ayudar a rechazar algunas especificaciones erróneas o indeseables. Aquellos que deseen indicar tipos deben proporcionar dicha información a través de la notación disponible en FOL. Si lo hace, puede hacer que tales expresiones más complejas, y también puede ser fácil equivocarse.
Predicados Single-parámetro se puede utilizar para implementar la noción de tipos en su caso. Por ejemplo, en: 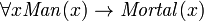 el predicado
el predicado 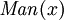 puede ser considerado una especie de "tipo de afirmación" (es decir, que
puede ser considerado una especie de "tipo de afirmación" (es decir, que 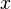 debe haber un hombre). Los predicados también se puede utilizar con la "existe" cuantificador para identificar los tipos, pero esto generalmente se debe hacer con el "y" operador en lugar, por ejemplo:
debe haber un hombre). Los predicados también se puede utilizar con la "existe" cuantificador para identificar los tipos, pero esto generalmente se debe hacer con el "y" operador en lugar, por ejemplo: 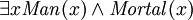 ("no existe algo que es a la vez un hombre y es mortal"). Es fácil de escribir
("no existe algo que es a la vez un hombre y es mortal"). Es fácil de escribir 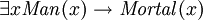 , pero esto sería equivalente a
, pero esto sería equivalente a  ("hay algo que no es un hombre, y / o existe algo que es mortal"), que normalmente no es lo que se pretendía. Del mismo modo, las afirmaciones pueden hacer que un tipo es un subtipo de otro tipo, por ejemplo:
("hay algo que no es un hombre, y / o existe algo que es mortal"), que normalmente no es lo que se pretendía. Del mismo modo, las afirmaciones pueden hacer que un tipo es un subtipo de otro tipo, por ejemplo:  ("para todos
("para todos  , si
, si  es un hombre, entonces
es un hombre, entonces 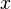 es un mamífero ").
es un mamífero ").
Dificultad en la finitud o rendición de caracterización
Se desprende de lo Löwenheim-Skolem teorema de que no es posible caracterizar finitud o rendición en la lógica de primer orden. Por ejemplo, en la lógica de primer orden no se puede afirmar la propiedad menos superior con destino a conjuntos de números reales , que establece que todos los delimitada, conjunto no vacío de números reales tiene un supremo; La se necesita la lógica de segundo orden para eso.
Graph accesibilidad no se puede expresar
Muchas situaciones pueden ser modeladas como un gráfico de nodos y conexiones dirigidas (bordes). Por ejemplo, la validación de muchos sistemas requiere que demuestra que un estado "malo" no se puede llegar desde un estado "bueno", y estas interconexiones de los estados a menudo puede ser modelado como un gráfico. Sin embargo, se puede demostrar que la conexión no puede expresarse plenamente en la lógica de predicados. En otras palabras, no existe una fórmula predicado-lógica 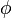 y
y 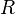 como su único símbolo predicado (de aridad 2) de tal manera que
como su único símbolo predicado (de aridad 2) de tal manera que 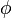 sostiene en una interpretación
sostiene en una interpretación  si y sólo si la extensión de
si y sólo si la extensión de  en
en  describe un gráfico conectado: es decir, gráficas conectados pueden no ser axiomatizada.
describe un gráfico conectado: es decir, gráficas conectados pueden no ser axiomatizada.
Nótese que dada una relación binaria que codifica un gráfico, se puede describir
que codifica un gráfico, se puede describir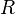 en términos de un conjunto de fórmulas de primer orden, y escribir una fórmula
en términos de un conjunto de fórmulas de primer orden, y escribir una fórmula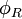 que es satisfiable si y sólo si
que es satisfiable si y sólo si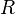 está conectado.
está conectado.
Comparación con otras lógicas
- Lógica de primer orden con tipo permite variables y términos que tienen distintos tipos (o clases ). Si sólo hay un número finito de tipos, esto realmente no difiere mucho de la lógica de primer orden, porque uno puede describir los tipos con un número finito de predicados unarios y algunos axiomas. A veces hay un tipo Ω especial de valores de verdad, en el que las fórmulas de casos son sólo términos de tipo Ω.
- La lógica de primer orden con las condiciones de dominio agrega condiciones de dominio (DC) a la lógica de primer orden clásico, lo que permite el manejo de las funciones parciales; estas condiciones pueden ser probados "en el lado" de una manera similar a las condiciones de tipo de corrección del PVS. También agrega if-then-else para mantener definiciones y pruebas manejables (llegaron a ser demasiado complejo sin ellos).
- El estándar SMT-LIB define un lenguaje utilizado por muchos grupos de investigación para las teorías de módulo satisfacibilidad; la lógica completa se basa en FOL con la igualdad, pero añade ordena (tipos), if-then-else para los términos y fórmulas (ite () y si .. entonces .. otra cosa ..), un let construyen para los términos y fórmulas ( y dejar que flet), y una clara construcción declarar un conjunto de valores que figuran como distinta. Sus conectores son no , implica , y , o , xor , y si y sólo si .
- Lógica de segundo orden débilpermite la cuantificación sobre subconjuntos finitos.
- Lógica de segundo orden Monádicapermite la cuantificación sobre subconjuntos, o en otras palabras másunariospredicados.
- La lógica de segundo orden permite la cuantificación sobre subconjuntos y las relaciones, o en otras palabras más de todos los predicados. Por ejemplo, el axioma de extensionalidad puede afirmar en la lógica de segundo orden que x = y ≡ def
 P ( P ( x ) ↔ P ( y )). Las fuertes semántica de la lógica de segundo orden dan tales oraciones un significado mucho más fuerte que la semántica de primer orden.
P ( P ( x ) ↔ P ( y )). Las fuertes semántica de la lógica de segundo orden dan tales oraciones un significado mucho más fuerte que la semántica de primer orden. - Lógicas de orden superior permite la cuantificación sobre los tipos más altos que de segundo orden permisos lógicas. Estos tipos más altos son las relaciones entre las relaciones, las funciones de las relaciones a las relaciones entre las relaciones, etc.
- Lógica de primer orden intuicionista utiliza intuicionista en lugar de cálculo proposicional clásica; por ejemplo, ¬¬φ no necesita ser equivalente a φ. Del mismo modo, primer orden lógicas fuzzy son extensiones de primer orden de la lógica fuzzy proposicionales en lugar de la lógica clásica.
- La lógica modaltiene extrasoperadores modalescon significados que se pueden caracterizar de manera informal como, por ejemplo, "es necesario que φ" y "es posible que φ".
- En cálculo de predicados monádicopredicados se limitan a tener un solo argumento.
- Lógica infinitary permite oraciones infinitamente largos. Por ejemplo, se puede permitir que una conjunción o disyunción de una infinidad de fórmulas o cuantificación sobre una infinidad de variables. Infinitamente frases largas surgen en áreas de las matemáticas, incluyendo la topología y la teoría de modelos.
- La lógica de primer orden con cuantificadores adicionalestiene nuevas cuantificadoresQx, ..., con significados como "hay muchosxtal que ... ". Véase también cuantificadores de ramificación y loscuantificadores plurales deGeorge Boolos y otros.
- Predicado lógica con definiciones (PLD, o D-lógica) modifica FOL agregando formalmente definiciones sintácticas como un tipo de valor (además de fórmulas y términos); estas definiciones se pueden utilizar dentro de los términos y fórmulas.
- Lógica Independencia amistosase caracteriza porcuantificadores de ramificación, que le permiten a uno para expresar la independencia entre las variables cuantificadas.
La mayor parte de estas lógicas se encuentran en algunas extensiones de los sentidos de FOL: incluyen todos los cuantificadores y operadores lógicos de FOL con el mismo significado. Lindström mostró que FOL no tiene extensiones (que no sean en sí) que satisfacen tanto el teorema de compacidad y la baja teorema Löwenheim-Skolem. Una declaración precisa del teorema de Lindström requiere algunas condiciones técnicas que la lógica se supone satisfacer; por ejemplo, el cambio de los símbolos de una lengua debe hacer ninguna diferencia esencial para que las oraciones son verdaderas.
Algebraizations
Tres formas de eliminar las variables cuantificadas de FOL, y que no implican la sustitución de cuantificadores con otros operadores variables vinculantes plazo, son conocidos:
- Álgebra cilíndrico, porAlfred Tarski y sus compañeros de trabajo;
- Álgebra poliádicos, porPaul Halmos;
- La lógica de predicados funtor, debido principalmente aWillard Quine.
Estasálgebras:
- ¿Son todas las extensiones propias de lade dos elementos álgebra de Boole, y por lo tanto soncelosías;
- Hacer por FOL lohace Lindenbaum-Tarski álgebra dela lógica proposicional;
- Permitir resultados deálgebra abstracta,álgebra universal, yla teoría para ser ejercida sobre FOL.
Tarski y Givant (1987) muestran que el fragmento de FOL que no tiene sentencia atómica tumbado en el ámbito de aplicación de más de tres cuantificadores, tiene el mismo poder expresivo como álgebra relación. Este fragmento es de gran interés, ya que es suficiente para la aritmética de Peano y más teoría axiomática de conjuntos , incluyendo el canónica ZFC. También demuestran que FOL con una primitiva par ordenado es equivalente a un álgebra de relación con dos pares ordenados funciones de proyección.
Automatización
Teorema de pruebas para la lógica de primer orden es uno de los subcampos más maduros de demostración automática de teoremas. La lógica es lo suficientemente expresiva para permitir la especificación de los problemas arbitrarias, a menudo en una forma razonablemente natural e intuitiva. Por otro lado, todavía es semidecidable, y un número de sonido y completos los cálculos se han desarrollado, permitiendo sistemas totalmente automatizados. En 1965 J. Alan Robinson logró un importante avance con su enfoque de resolución; para demostrar un teorema que trata de refutar el teorema negada, de una manera dirigida a objetivos, lo que resulta en un método mucho más eficaz para demostrar teoremas automáticamente en FOL. Lógicas más expresivos, como de orden superior y lógicas modales, permiten la expresión práctica de una amplia gama de problemas que la lógica de primer orden, pero el teorema de pruebas para estas lógicas está menos desarrollado.
Una nueva tecnología moderna y particularmente perjudicial es el desolucionadores de SMT, que se suman la aritmética y el apoyo de proposiciones a las clases poderosas desolucionadores SAT.