
Symétrie
Contexte des écoles Wikipédia
Enfants SOS ont produit une sélection d'articles de wikipedia pour les écoles depuis 2005. SOS enfants est le plus grand organisme de bienfaisance dans le monde en donnant aux enfants orphelins et abandonnés la chance de la vie familiale.

Symétrique dans l'usage commun transmet généralement deux significations primaires. Le premier est un sens imprécis de proportionnalité et équilibre harmonieux ou esthétique, qui; de telle sorte qu'il reflète la beauté ou de la perfection. Le deuxième sens est un concept précis et bien défini d'équilibre ou de "motifs auto-similarité" qui peut être démontré ou prouvé selon les règles d'un système formel: par la géométrie , à travers la physique ou autrement.
Bien que les significations sont à distinguer, dans certains contextes, les deux significations de «symétrie» sont liées et discutés en parallèle.
Les notions "précises" de symétrie ont diverses mesures et les définitions opérationnelles. Par exemple, la symétrie peut être observé:
- en ce qui concerne le passage du temps ;
- comme un relation spatiale;
- travers géométrique tels que les transformations mise à l'échelle, réflexion, et rotation;
- par d'autres types de transformations fonctionnelles; et
- en tant qu'élément de des objets abstraits, modèles théoriques, la langue , la musique et même connaissance elle-même.
Cet article décrit ces notions de symétrie à partir de trois perspectives. Le premier est celui de mathématiques , dans lequel symétries sont définis et classés avec précision. La seconde perspective décrit symétrie en ce qui concerne la science et la technologie . Dans ce contexte, symétries sous-tendent certains des résultats les plus profondes de moderne physique , y compris les aspects de espace et le temps. Enfin, une troisième perspective discute symétrie dans les sciences humaines , couvrant son utilisation riche et variée dans l'histoire , l'architecture , l'art et la religion .
Le contraire de la symétrie est asymétrie.
Symétrie en mathématiques
Sur le plan formel, nous disons qu'un objet est symétrique par rapport à une donnée opération mathématique, si, lorsqu'elle est appliquée à l'objet, cette opération ne change pas l'objet ou de son apparence. Deux objets sont symétriques les unes aux autres par rapport à un groupe donné d'opérations si l'on obtient à partir de l'autre par une partie des opérations (et vice versa).
Symétries peuvent également être trouvés dans les organismes vivants, y compris les humains et les autres animaux (voir la symétrie en biologie ci-dessous). En géométrie 2D les principaux types de symétrie d'intérêt sont par rapport à la base Euclidiennes isométries planes: traductions, rotations, réflexions, et glisser réflexions.
Modèle mathématique pour la symétrie
L'ensemble des opérations de symétrie considérée, sur tous les objets dans un ensemble X, peut être modélisée comme une l'action Groupe G: G × X → X, où l'image de g dans G et x dans X se écrit g · x. Si, pour une g, g · x = y, alors x et y sont dits être symétriques l'une de l'autre. Pour chaque objet x, opérations pour lesquelles g g · x = x former un groupe , le groupe de symétrie de l'objet, un sous-groupe de G. Si le groupe de symétrie de x est le groupe trivial alors x est dite asymétrique, sinon symétrique. Un exemple général est que G est un groupe de bijections g: V → V agissant sur l'ensemble des fonctions x: V → W par (gx) (v) = x (g -1 (v)) (ou un ensemble restreint de ces fonctions qui est fermé sous l'action de groupe). Ainsi, un groupe de bijections de l'espace induit une action de groupe sur les "objets" en elle. Le groupe de symétrie de x se compose de tous g pour lesquels x (v) = x (g (v)) pour tout v. G est le groupe de symétrie de l'espace lui-même, et de tout objet qui est uniforme dans tout l'espace. Certains sous-groupes de G peuvent ne pas être le groupe de symétrie d'un objet quelconque. Par exemple, si le groupe contient pour chaque v et w dans un V g telle que g (v) = w, alors que les groupes de symétrie des fonctions constantes x contiennent ce groupe. Toutefois, le groupe de symétrie des fonctions constantes G est elle-même.
Dans une version modifiée de champs de vecteurs, on a (gx) (v) = h (x (g, g -1 (v))) où h tourne tous les vecteurs et pseudovectors en x, et inverse des vecteurs (mais pas pseudovectors) selon la rotation et l'inversion en g, voir symétrie en physique. Le groupe de symétrie x se compose de tous g pour lesquels X (v) = h (x, g (g (v))) pour tous les v. Dans ce cas, le groupe de symétrie d'une fonction constante peut être un sous-groupe convenable de G: un vecteur constant a seulement une symétrie de rotation par rapport à la rotation autour d'un axe si cet axe est dans la direction du vecteur, et que la symétrie d'inversion si elle est zéro.
Pour une notion commune de la symétrie dans l'espace euclidien , G est le Groupe euclidien E (n), le groupe de isométries, et V est l'espace euclidien. Le groupe d'un objet de rotation est le groupe de symétrie si G est limitée à E + (n), le groupe des isométries directes. (Pour généralisations, voir le prochain paragraphe.) Les objets peuvent être modélisés comme des fonctions x, dont une valeur peut représenter une sélection de propriétés telles que la couleur, la densité, composition chimique, etc., selon la sélection que nous considérons seulement symétries d'ensembles de points (x est juste un fonction booléenne de la position v), ou, à l'autre extrême, par exemple symétrie de droite et main gauche avec toute leur structure.
Pour un groupe de symétrie donnée, les propriétés d'une partie de l'objet, définissent complètement la totalité de l'objet. Compte tenu des points équivalent qui, en raison de la symétrie, les mêmes propriétés, les classes d'équivalence sont les orbites de l'action de groupe sur l'espace lui-même. Nous avons besoin de la valeur de x à un point dans chaque orbite pour définir l'objet complet. Un ensemble de ces représentants forme une domaine fondamental. Le plus petit domaine fondamental n'a pas une symétrie; dans ce sens, on peut dire que la symétrie se appuie sur asymétrie.
Un objet avec une symétrie désiré peut être produit en choisissant pour chaque orbite une valeur de fonction unique. À partir d'un objet x donné que nous pouvons par exemple:
- prendre les valeurs dans un domaine fondamental (ie, ajouter des copies de l'objet)
- prendre pour chaque orbite une sorte de moyenne ou la somme des valeurs de x aux points de l'orbite (idem, où les copies peuvent se chevaucher)
Se il est désiré de ne pas avoir plus de symétrie que dans le groupe de symétrie, puis l'objet à copier doit être asymétrique.
Comme indiqué plus haut, certains groupes de isometries ne sont pas le groupe de symétrie d'un objet quelconque, sauf dans le modèle modifié de champs de vecteurs. Par exemple, cela se applique en 1D pour le groupe de toutes les traductions. Le domaine fondamental est un seul point, nous ne pouvons pas faire asymétrique, de sorte que toute "pattern" invariante par translation est également invariante par réflexion (ce sont les "modèles" uniformes).
Dans la version de vecteur champ symétrie de translation continue ne implique pas symétrie de réflexion: la valeur de fonction est constante, mais se il contient des vecteurs non nuls, il n'y a pas symétrie de réflexion. Se il n'y a également symétrie de réflexion, la valeur de la fonction constante ne contient pas de vecteurs non nuls, mais il peut contenir pseudovectors non nuls. Un exemple 3D correspondant est un infini cylindre avec un courant perpendiculaire à l'axe; la champ magnétique (une pseudo-vecteur) est, dans la direction du cylindre, constante, mais différente de zéro. Pour les vecteurs (en particulier le densité de courant), on a une symétrie dans chaque plan perpendiculaire au cylindre, ainsi que la symétrie cylindrique. Cette symétrie cylindrique sans plans de miroir à travers l'axe est également possible que dans la version du champ de vecteurs de la notion de symétrie. Un exemple similaire est un cylindre tournant autour de son axe, où le champ magnétique et la densité de courant sont remplacés par le moment angulaire et de vitesse , respectivement.
Un groupe de symétrie est dit transitivement à agir sur une fonction d'un objet répété si, pour chaque paire d'occurrences de l'élément il existe une opération de symétrie cartographie de la première à la seconde. Par exemple, en 1D, le groupe de symétrie du {..., 1,2,5,6,9,10,13,14, ...} est transitif sur tous ces points, tandis que {..., 1, 2,3,5,6,7,9,10,11,13,14,15, ...} ne agit pas transitivement sur tous les points. Équivalente, la première série est seule classe conjugaison par rapport à isometries, tandis que le second a deux classes.
Symétrie non-isométrique
Comme mentionné ci-dessus, G (le groupe de symétrie de l'espace lui-même) peut différer de la Groupe euclidien, le groupe de isométries.
Exemples:
- G est le groupe de transformations de similarité, soit transformations affines avec une matrice A qui est une fois un scalaires matrice orthogonale. Ainsi dilatations sont ajoutés, auto-similarité est considéré comme une symétrie
- G est le groupe de transformations affines avec une matrice A de déterminant 1 ou -1, ce est à dire la transformation qui préservent zone; ce qui ajoute par exemple oblique symétrie de réflexion.
- G est le groupe de toutes les transformations affines bijectives
- En Inversion, G inclut des réflexions de cercle, etc.
- Plus généralement, un involution définit une symétrie par rapport à cette involution.
Symétrie directionnelle
Voir symétrie directionnelle.
Symétrie de réflexion
Voir symétrie de réflexion.
Symétrie de réflexion, la symétrie miroir, image-miroir symétrie, ou symétrie bilatérale est une symétrie par rapport à la réflexion.
Ce est le type le plus commun de symétrie. En 2D, il ya un axe de symétrie, en 3D d'un plan de symétrie. Un objet ou une figure qui ne se distingue pas de son image transformée est appelé miroir symétrique (voir image miroir).
L'axe de symétrie d'une figure à deux dimensions est une ligne de telle sorte que, si une perpendiculaire est construit, deux points quelconques situés sur la perpendiculaire à égale distance de l'axe de symétrie sont identiques. Une autre façon de penser, ce est que si la forme devait être plié en deux sur l'axe, les deux moitiés seraient identiques: les deux moitiés sont l'image de l'autre dans un miroir. Ainsi, un carré a quatre axes de symétrie, car il ya quatre façons différentes de le plier et ont les bords durant tout le match. Un cercle a une infinité de axes de symétrie, pour la même raison.
Si la lettre T est réfléchi le long d'un axe vertical, il apparaît les mêmes. Notez que ce est parfois appelé symétrie horizontale, et la symétrie verticale parfois! On peut mieux utiliser une formulation sans ambiguïté, par exemple "T a un axe de symétrie vertical."
Les triangles avec cette symétrie est isocèle , les quadrilatères avec cette symétrie est le cerfs-volants et les isocèle trapèzes.
Pour chaque ligne ou plan de réflexion, le groupe de symétrie est isomorphe avec Cs (voir groupes de points en trois dimensions), l'un des trois types d'ordre deux (involutions), donc algébriquement C2. Le domaine fondamentale est un demi-plan ou demi-espace.
Bilateria bilatéraux (animaux, y compris l'homme) sont plus ou moins symétrique par rapport à la plan sagittal.
Dans certains contextes, il est une symétrie de rotation de toute façon. Puis symétrie spéculaire est équivalent à symétrie d'inversion; dans de tels contextes physique moderne le terme P-symétrie est utilisé pour les deux (P = parité).
Pour plus de types généraux de réflexion il ya des types plus généraux de symétrie de réflexion correspondant. Exemples:
- par rapport à une non isométrique affine involution (une réflexion oblique en ligne, avion, etc.).
- en ce qui concerne cercle inversion
La symétrie de rotation
Voir une symétrie de rotation.
La symétrie de rotation est symétrie par rapport à une partie ou toutes les rotations en dimension m espace euclidien. Rotations sont isométries directes, ce est à dire, isométries préservant orientation. Par conséquent, un groupe de symétrie de la symétrie de rotation est un sous-groupe de E + (m) (voir Groupe euclidienne).
Symétrie par rapport à toutes les rotations sur tous les points implique la symétrie de translation par rapport à toutes les traductions, et le groupe de symétrie est l'ensemble E + (m). Cela ne se applique pas pour les objets car il rend l'espace homogène, mais elle peut se appliquer des lois physiques.
Pour symétrie par rapport aux rotations autour d'un point nous pouvons prendre ce point comme origine. Ces rotations constituent le groupe spécial orthogonal SO (m), le groupe de m × m avec matrices orthogonales déterminant une. Pour m = 3 ce est la groupe rotation.
Dans un autre sens du mot, le groupe d'un objet de rotation est le groupe de symétrie au sein de E + (n), le groupe des isométries directes; en d'autres termes, l'intersection du groupe de symétrie complète et le groupe des isométries directes. Pour les objets chiraux il est le même que le groupe de symétrie complète.
Lois de la physique sont SO (3) -invariante se ils ne distinguent pas des directions différentes dans l'espace. À cause de Le théorème de Noether, la symétrie de rotation d'un système physique est équivalente à la loi angulaire de conservation de quantité de mouvement. Voir également invariance par rotation.
Symétrie de translation
Voir l'article principal symétrie de translation.
Symétrie de translation laisse un invariant de l'objet sous un groupe discret ou continu de traductions 
Glide symétrie de réflexion
Un glisse symétrie de réflexion (en 3D: un plan de symétrie de descente) signifie qu'un reflet dans une ligne ou un plan combiné à une translation le long de la ligne / dans le plan, les résultats dans le même objet. Elle implique la symétrie de translation par deux fois le vecteur de translation.
Le groupe de symétrie est isomorphe avec Z.
Rotoreflection symétrie
En 3D, ou rotoreflection Antirotation au sens strict est une rotation autour d'un axe, combinée avec la réflexion dans un plan perpendiculaire à cet axe. Comme groupes de symétrie en ce qui concerne un roto-réflexion, nous pouvons distinguer:
- l'angle ne est pas commun diviseur à 360 °, le groupe de symétrie ne est pas discrète
- 2 n -fois rotoreflection (angle de 180 ° / n) avec le groupe de symétrie S 2n d'ordre 2 n (à ne pas confondre avec groupes symétriques, pour lesquels la même notation est utilisée; abstraite groupe C 2n); un cas particulier est n = 1, inversion, car elle ne dépend pas de l'axe et le plan, il est caractérisé par que le point d'inversion.
- C NH (angle de 360 ° / n); pour n impair ce est générée par une seule symétrie, et le groupe est abstraite C 2n, même pour n ce ne est pas une symétrie de base, mais une combinaison. Voir également groupes de points en trois dimensions.
Symétrie hélicoïdale

Symétrie hélicoïdale est le genre de symétrie vu dans ces objets du quotidien que ressorts, Jouets Slinky, forets, et tarières. Il peut être considéré comme une symétrie de rotation avec translation le long de l'axe de rotation, la axe de la vis). Le concept de symétrie hélicoïdale peut être visualisé comme le tracé tridimensionnel dans l'espace qui résulte de la rotation d'un objet à un même vitesse angulaire tout en se déplaçant simultanément à une autre vitesse, même le long de son axe de rotation (traduction). A tout moment, ces deux motions se combinent pour donner un angle d'enroulement qui aide à définir les propriétés du tracé. Lorsque l'objet de traçage tourne rapidement et traduit lentement, l'angle d'enroulement sera proche de 0 °. A l'inverse, si la rotation est lente et rapide la traduction, l'angle d'enroulement se approcher de 90 °.
Trois grandes classes de symétrie hélicoïdale peuvent être différencié en fonction du jeu de l'angle d'enroulement et de traduction symétries long de l'axe:
- Infini symétrie hélicoïdale. Se il n'y a pas de caractéristiques distinctives le long de la longueur d'un hélice ou un objet de type hélice, l'objet auront symétrie infinie peu comme celle d'un cercle, mais avec l'exigence supplémentaire de translation le long de l'axe long de l'objet à retourner à son aspect d'origine. Un objet de type hélice est celui qui a à chaque point de l'angle de l'enroulement régulier d'une hélice, mais qui peut aussi avoir un indéfiniment section transversale de grande complexité, à la condition seulement que ce est précisément la même section transversale existe (en général après une rotation) en tout point le long de la longueur de l'objet. Voici quelques exemples simples uniformément enroulés ressorts, Slinky, forets, et tarières. Dit plus précisément, un objet a symétries infinies hélicoïdales si pour une petite rotation de l'objet autour de son axe central, il existe un point à proximité (la distance de translation) sur cet axe au cours de laquelle l'objet apparaîtra exactement comme avant. Ce est cette infinie symétrie hélicoïdale qui donne lieu à l'illusion curieux de mouvement le long de la longueur d'un bit de la vis ou de la vis qui est entraînée en rotation. Il offre également la possibilité mécaniquement utile de ces dispositifs pour déplacer les matériaux le long de leur longueur, à condition qu'elles soient combinées avec une force telle que la gravité ou de frottement qui permet de résister à des matériaux avec une simple rotation du foret ou une tarière.
- n-symétrie hélicoïdale. Si l'exigence que chaque section transversale de l'objet hélicoïdale être identique est détendue, symétries hélicoïdaux moins supplémentaires deviennent possibles. Par exemple, la section transversale de l'objet en hélice peut être modifié, mais encore se répète de manière régulière le long de l'axe hélicoïdal de l'objet. Par conséquent, les objets de ce type vont présenter une symétrie après une rotation d'un certain angle fixe
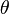 et une traduction d'une certaine distance fixe, mais ne sera pas en général être invariant de ne importe quel angle de rotation. Si l'angle (rotation) au cours de laquelle la symétrie se divise uniformément dans un cercle complet (360 °), le résultat est l'équivalent hélicoïdale d'un polygone régulier. Ce cas est appelé n-symétrie hélicoïdale, où n = 360 ° /
et une traduction d'une certaine distance fixe, mais ne sera pas en général être invariant de ne importe quel angle de rotation. Si l'angle (rotation) au cours de laquelle la symétrie se divise uniformément dans un cercle complet (360 °), le résultat est l'équivalent hélicoïdale d'un polygone régulier. Ce cas est appelé n-symétrie hélicoïdale, où n = 360 ° / 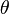 , Voir par exemple double hélice. Ce concept peut encore être généralisée à inclure les cas où
, Voir par exemple double hélice. Ce concept peut encore être généralisée à inclure les cas où 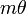 est un multiple de 360 °, ce est-, le cycle ne se répète par la suite, mais seulement après plus d'un tour complet de l'objet hélicoïdale.
est un multiple de 360 °, ce est-, le cycle ne se répète par la suite, mais seulement après plus d'un tour complet de l'objet hélicoïdale.
- Non répétable symétrie hélicoïdale. Ce est le cas dans lequel l'angle de rotation
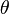 tenue de respecter la symétrie est un nombre irrationnel comme
tenue de respecter la symétrie est un nombre irrationnel comme 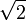 radians que ne se répète jamais exactement ne importe combien de fois l'hélice tourne. Ces symétries sont créés en utilisant un non répétable Point groupe en deux dimensions. ADN est un exemple de ce type de symétrie non-répétition hélicoïdale.
radians que ne se répète jamais exactement ne importe combien de fois l'hélice tourne. Ces symétries sont créés en utilisant un non répétable Point groupe en deux dimensions. ADN est un exemple de ce type de symétrie non-répétition hélicoïdale.
La symétrie d'échelle et fractales
La symétrie d'échelle renvoie à l'idée que si un objet est agrandie ou réduite en taille, le nouvel objet a les mêmes propriétés que l'original. La symétrie d'échelle est notable pour le fait qu'il ne existe pas pour la plupart des systèmes physiques, un point qui a d'abord été perçue que par Galileo . Des exemples simples de l'absence de symétrie d'échelle dans le monde physique comprennent la différence dans la force et la taille des jambes de éléphants contre les souris , et l'observation que si une bougie en cire molle a été agrandi à la taille d'un grand arbre, il se effondrerait immédiatement sous son propre poids.
Une forme plus subtile de symétrie d'échelle est démontrée par fractales . Comme conçu par Mandelbrot, fractales sont un concept mathématique dans lequel la structure d'une forme complexe ressemble exactement la même, peu importe le degré de grossissement est utilisé pour l'examiner. Un côte est un exemple de fractale naturelle, car il conserve à peu près comparable et d'apparence semblable complexité à tous les niveaux de la vue d'un satellite à un examen microscopique de la façon dont l'eau clapote contre grains individuels de sable. La ramification des arbres, qui permet aux enfants d'utiliser de petites brindilles que stand-ins pour arbres entiers dans dioramas, est un autre exemple.
Cette similitude de phénomènes naturels fournit des fractales avec une familiarité quotidienne généralement pas vu avec fonctions générées mathématiquement. En conséquence, ils peuvent produire une beauté frappante des résultats tels que l' ensemble de Mandelbrot . Curieusement, fractales ont également trouvé une place dans CG, ou les effets des films générés par ordinateur, où leur capacité à créer des courbes très complexes avec symétries fractales résultats dans plus réaliste mondes virtuels.
combinaisons de symétrie
Voir combinaisons de symétrie.
Symétrie dans la science
Symétrie en physique
Symétrie en physique a été généralisée pour signifier invariance qui est, le manque de tout changement pour l'application visible tout type de transformation. Ce concept est devenu l'un des outils les plus puissants de la physique théorique, car il est devenu évident que pratiquement toutes les lois de la nature proviennent de symétries. En fait, ce rôle a inspiré le lauréat du prix Nobel PW Anderson à écrire dans son très lu l'article 1972 Plus est différent que «ce ne est exagéré légèrement le cas de le dire que la physique est l'étude de symétrie." Voir Théorème de Noether (qui, comme une simplification grossière, stipule que pour chaque symétrie mathématique continue, il ya une quantité conservée correspondant; un courant conservé, dans la langue originale de Noether); et aussi, La classification de Wigner, qui dit que les symétries des lois de la physique déterminent les propriétés des particules trouvées dans la nature.
Symétrie dans les objets physiques
Objets classiques
Même si un objet usuel peut apparaître exactement le même après une opération de symétrie comme une rotation ou un échange de deux parties identiques a été réalisée sur lui, il est évident qu'une telle symétrie est vrai seulement comme une approximation pour tout objet physique ordinaire.
Par exemple, si une tourne un aluminium usiné avec précision triangle équilatéral de 120 degrés autour de son centre, un observateur occasionnel mis en avant et après la rotation sera incapable de décider si oui ou non une telle rotation a eu lieu. Cependant, la réalité est que chaque coin d'un triangle apparaîtra toujours unique lorsque examiné avec suffisamment de précision. Un observateur armé avec des équipements de mesure suffisamment détaillés tels que optique ou microscopes électroniques ne seront pas dupes; il reconnaîtra immédiatement que l'objet a été mis en rotation par la recherche de détails tels que des cristaux ou des déformations mineures.
Si simple expériences de pensée montrent que les affirmations de symétrie dans les objets physiques quotidiennes sont toujours une question de similitude approximative plutôt que de similitude mathématique précise. La conséquence la plus importante de cette nature approximative des symétries dans les objets physiques quotidiennes est que ces symétries ont peu d'impacts ou pas sur la physique de ces objets. Par conséquent, seul le plus profond symétries d'espace et le temps jouent un rôle majeur dans la physique qui est classique, la physique des grandes, des objets du quotidien.
Objets quantiques
Remarquablement, il existe un domaine de la physique pour lequel affirmations mathématiques de symétries simples objets réels cessent d'être des approximations. Ce est le domaine de la physique quantique , qui, pour la plupart, est la physique des objets très petits, très simples telles que des électrons , protons , la lumière , et atomes .
Contrairement aux objets de tous les jours, des objets tels que les électrons ont un nombre très limité de configurations, appelé états, dans lesquels ils peuvent exister. Cela signifie que lorsque les opérations de symétrie comme l'échange les positions des composants leur sont appliquées, les nouvelles configurations résultant souvent ne peuvent pas être distingués des originaux ne importe comment diligente une observateur. Par conséquent, pour les petites et suffisamment simples objets l'affirmation de symétrie mathématique générique F (x) = x cesse d'être approximative, et devient à la place une description expérimentale précise et exacte de la situation dans le monde réel.
Conséquences de symétrie quantique
Se il est logique que les symétries pourraient devenir exacte lorsqu'elle est appliquée à des objets très simples, l'intuition immédiate est qu'un tel détail ne devrait pas affecter la physique de ces objets de manière significative. Ce est en partie parce qu'il est très difficile de voir la notion de similitude exacte que physiquement significative. Notre image mentale de ces situations est toujours le même que celui que nous utilisons pour les objets volumineux: Nous représentons des objets ou des configurations qui sont très, très semblable, mais pour lesquels si nous pouvions "regarder de plus près" nous serions encore en mesure de faire la différence.
Toutefois, l'hypothèse que les symétries exactes dans de très petits objets ne devraient pas faire de différence dans leur physique a été découvert dans les années 1900 pour être spectaculaire incorrect. La situation a été succinctement résumée par Richard Feynman dans les transcriptions directes de son Feynman Cours de Physique, Volume III, section 3.4, particules identiques. (Malheureusement, la citation a été édité sur la version imprimée de la même conférence.)
- "... Se il ya une situation physique dans lequel il est impossible de dire de quel côté il est arrivé, il interfère toujours; il ne manque jamais."
Le mot " interfère »dans ce contexte est un moyen rapide de dire que ces objets tombent sous les règles de la mécanique quantique , dans laquelle ils se comportent plus comme des ondes qui interfèrent que comme tous les jours de grands objets.
En bref, quand un objet devient si simple que une assertion de la symétrie de la forme F (x) = x devient une déclaration exacte de la mêmeté expérimentalement vérifiables, x cesse de suivre les règles de la physique classique et doit plutôt être modélisé en utilisant les règles-intuitive plus complexes et souvent beaucoup moins de la physique quantique .
Cette transition fournit également des indications importantes sur la raison pour laquelle les mathématiques de symétrie sont si profondément imbriqués avec ceux de la mécanique quantique. Lorsque les systèmes physiques à faire la transition de symétries qui sont environ à ceux qui sont exacte, les expressions mathématiques de ces symétries cessent d'être des approximations et sont transformés en définitions précises de la nature sous-jacente des objets. A partir de là, la corrélation de ces objets à leurs descriptions mathématiques devient si étroite qu'il est difficile de séparer les deux.
Symétrie comme principe unificateur de la géométrie
Le géomètre allemand Felix Klein énoncé un très influent Programme d'Erlangen en 1872, ce qui suggère que la symétrie unification et principe organisateur dans la géométrie (à un moment où cela a été lu «géométries»). Ce est un large plutôt que de principe profond. Initialement, il a conduit à l'intérêt pour les groupes attachés à géométries, et le slogan la géométrie de la transformation (un aspect de la New Math, mais guère controversée dans la pratique mathématique moderne). A présent, il a été appliqué dans de nombreuses formes, comme une sorte d'attaque standard sur les problèmes.
Symétrie en mathématiques
Un exemple d'une expression mathématique présentant une symétrie est un ² c + 3 ab + b ² c. Si A et B sont échangées, l'expression reste inchangé en raison de la commutativité de l'addition et la multiplication.
Comme dans la géométrie, pour les termes il ya deux possibilités:
- il est lui-même symétrique
- il a un ou plusieurs autres termes symétriques avec elle, en fonction du type de symétrie
Voir également fonction symétrique, la dualité (mathématiques)
Symétrie dans la logique
Un relation dyadique R est symétrique si et seulement si, chaque fois que ce est vrai que Rab, il est vrai que Rba. Ainsi, "est le même âge que" est symétrique, car si Paul est du même âge que Marie, alors Marie est le même âge que Paul.
Binaire symétrique connecteurs logiques sont " et "(∧, 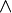 Ou &) ", ou "(∨)," biconditional "( ssi) (↔), NAND ("pas et"), XOR («non-biconditional"), et NOR ("pas-ou").
Ou &) ", ou "(∨)," biconditional "( ssi) (↔), NAND ("pas et"), XOR («non-biconditional"), et NOR ("pas-ou").
Généralisations de symétrie
Si nous avons un ensemble d'objets avec une certaine structure, alors il est possible pour une symétrie de convertir seulement un seul objet dans un autre, au lieu d'agir sur tous les objets possibles simultanément. Cela nécessite une généralisation du concept de groupe de symétrie à celle d'un groupoïde.
Les physiciens ont mis au point avec d'autres directions de la généralisation, comme supersymétrie et groupes quantiques.
Symétrie en biologie
Voir symétrie (biologie) et symétrie faciale.
Symétrie dans la chimie
Symétrie est important de la chimie parce qu'il explique observations à la spectroscopie , la chimie quantique et cristallographie. Il se appuie fortement sur la théorie des groupes .
Symétrie dans l'histoire, la religion et la culture
Dans toute entreprise humaine pour lequel un résultat visuel impressionnant, ce est une partie de l'objectif recherché, symétries jouent un rôle profonde. L'appel innée de symétrie peut être trouvée dans nos réactions se passe à travers des objets naturels très symétriques, tels que des cristaux formés précisément ou de coquillages magnifiquement spiralées. Notre première réaction à trouver un tel objet est souvent à se demander si nous avons trouvé un objet créé par un être humain, rapidement suivi par surprise que les symétries qui ont attiré notre attention sont dérivées de la nature elle-même. Dans les deux réactions nous donnons notre inclination pour voir symétries fois aussi belle et, d'une certaine façon, informative du monde qui nous entoure.
Symétrie dans les symboles religieux

La tendance des gens à voir fin en symétrie suggère au moins une des raisons pourquoi les symétries sont souvent partie intégrante des symboles des religions du monde. Juste un peu de nombreux exemples incluent le sextuplé symétrie de rotation judaïsme s ' Étoile de David, le double signaler symétrie du taoïsme s ' Taijitu ou Yin-Yang, le symétrie bilatérale du christianisme s ' traverser et le sikhisme s ' Khanda, ou le point de symétrie quadruple Ancienne (et pacifiquement prévu) version Jain de la croix gammée . Avec ses fortes interdictions contre l'utilisation d'images de représentation, l'islam , et dans le particulier Branche de l'islam sunnite, a mis au point certains de l'utilisation la plus complexe et visuellement impressionnant des symétries pour des utilisations décoratives de toute religion majeure.
L'ancien L'image Taijitu de taoïsme est une utilisation particulièrement fascinant de symétrie autour d'un point central, combinée avec inversion noir et blanc de la couleur à des distances opposées de ce point central. L'image, qui est souvent mal compris dans le Monde occidental comme représentant bonne (blanc) contre le mal (noir), est en fait conçu comme un représentant graphique de la nécessité complémentaire pour deux concepts abstraits de "masculinité" (blanc) et "féminité" (noir). La symétrie du symbole dans ce cas est utilisé non seulement pour créer un symbole qui attire l'attention de l'œil, mais de faire une déclaration importante sur les croyances philosophiques des personnes et des groupes qui l'utilisent. Aussi un symbole religieux important symétrique est le shintoïste "Torii" "La porte des oiseaux», habituellement la porte des temples shintoïstes appelés "Jinjas".
Symétrie dans les interactions sociales
Les gens observent la nature symétrique, y compris souvent équilibre asymétrique, des interactions sociales dans une variété de contextes. Il se agit notamment des évaluations de la réciprocité, de l'empathie, des excuses, de dialogue, le respect, la justice et la vengeance. Interactions symétriques envoient le message "nous sommes tous les mêmes" alors que les interactions asymétriques envoient le message "Je suis spéciale; mieux que vous". Les relations entre pairs sont basés sur la symétrie, les relations de pouvoir sont basées sur l'asymétrie.
Symétrie en architecture
Une autre activité humaine dans laquelle le résultat visuel joue un rôle essentiel dans le résultat global est l'architecture . Tant dans les temps anciens, la capacité d'une grande structure pour impressionner ou même intimider ses téléspectateurs a souvent été une partie importante de son objet, et l'utilisation de la symétrie est un aspect incontournable de la façon d'accomplir ces objectifs.
Voici quelques exemples d'anciens exemples d'architectures qui ont fait l'utilisation puissante de symétrie d'impressionner ceux qui les entourent inclus l' égyptienne Pyramides , le grec du Parthénon , et la première et la seconde Temple de Jérusalem, de la Chine Cité Interdite, le Cambodge d ' Angkor Wat complexe, et les nombreux temples et des pyramides de l'ancienne Civilisations précolombiennes. Exemples historiques plus récentes d'architectures soulignant symétries comprennent Cathédrales de l'architecture gothique, et américaine président Thomas Jefferson s ' Monticello la maison. Inde inégalée s Taj Mahal est dans une catégorie à part, car il peut sans doute être l'un des usages les plus impressionnants et beaux de symétrie dans l'architecture que le monde ait jamais vu.

Un exemple intéressant d'un symétrie brisée en architecture est la tour penchée de Pise , dont la notoriété découle en grande partie pas la symétrie destinée de sa conception, mais pour la violation de cette symétrie de la maigre qui se est développée alors qu'il était encore en construction. Des exemples modernes d'architectures qui font usage impressionnante ou complexe de diverses symétries comprennent l'Australie 's étonnante Sydney Opera House et Houston, au Texas 's simple Astrodome.
Symétrie trouve ses moyens dans l'architecture à toutes les échelles, des vues extérieures globales, à travers la mise en page de l'individu plans d'étage, et vers le bas à la conception d'éléments de construction individuelle tels que des portes finement cédé, vitraux , mosaïques de carreaux , frises, escaliers, rampes d'escalier, et balustradess. Pour complexité et la sophistication dans l'exploitation de symétrie comme un élément architectural, islamiques bâtiments tels que le Taj Mahal éclipsent souvent ceux d'autres cultures et d'âges, dû en partie à l'interdiction générale de l'Islam contre l'utilisation des images ou des personnes ou des animaux.
Liens relatifs à la symétrie dans l'architecture comprennent:
- Williams: Symétrie en architecture
- Aslaksen: Mathématiques en Art et Architecture
Symétrie dans la poterie et métalliques des navires

Depuis les premières utilisations de roues de poterie pour aider les vases d'argile de la forme, de la poterie a eu une forte relation de symétrie. Au minimum, la poterie créée en utilisant une roue commence nécessairement en pleine symétrie de rotation dans sa section transversale, tout en permettant une grande liberté de forme dans le sens vertical. Sur cette intrinsèquement symétriques cultures de point de départ de l'Antiquité ont eu tendance à ajouter d'autres modèles qui ont tendance à exploiter ou dans de nombreux cas de réduire la pleine symétrie de rotation d'origine à un point où un objectif visuelle spécifique est atteint. Par exemple, persan poterie datant du quatrième millénaire avant JC et utilisé précédemment zigzags symétriques, des carrés, hachures, et les répétitions de chiffres pour produire des modèles plus complexes et globaux frappantes visuellement.
Récipients métalliques exprimés manquaient la symétrie de rotation inhérente de la poterie fait au tour, mais autrement fourni une occasion similaire à décorer leurs surfaces avec des motifs agréables à ceux qui les ont utilisés. L'ancien Chinois, par exemple, utilisé des motifs symétriques dans leurs moulages en bronze dès le 17e navires siècle avant JC bronze exposées à la fois un motif principal bilatérale et une conception de la frontière traduit répétitif.
Liens:
- Chinavoc: L'art des bronzes chinois
- Grant: Poterie iranien à l'Institut oriental
- Le Metropolitan Museum of Art - art islamique
Symétrie dans des couvertures

Comme couettes sont fabriqués à partir de blocs carrés (habituellement 9, 16 ou 25 pièces pour un bloc) avec chaque pièce inférieure généralement constitué de triangles de tissu, le métier se prête facilement à la demande de symétrie.
Liens:
- Quate: exploration de la géométrie Grâce Quilts
Symétrie dans les tapis et moquettes

Une longue tradition de l'utilisation de la symétrie dans les tapis et les motifs tapis couvre une variété de cultures. Américain Indiens Navajo utilisé diagonales audacieuses et motifs rectangulaires. Beaucoup tapis orientaux ont des centres et des frontières complexes réfléchis qui se traduisent par un motif. Sans surprise, tapis rectangulaires utilisent généralement quadrilatère symétrie qui est, motifs qui sont reflétées dans les deux axes horizontaux et verticaux.
Liens:
- Mallet: tapis d'Orient tribaux
- Dilucchio: Navajo Rugs
Symétrie dans la musique
Symétrie est bien sûr pas limitée aux arts visuels. Son rôle dans l'histoire de la musique touche de nombreux aspects de la création et de la perception de la musique.
La forme musicale
Symétrie a été utilisé comme une contrainte formelle par de nombreux compositeurs, tels que la forme de la voûte (ABCBA) utilisée par Steve Reich, Béla Bartók, et James Tenney (ou de la houle). Dans la musique classique, Bach a utilisé les concepts de symétrie de permutation et invariance; voir (lien externe "Fugue No. 21," pdf ou Shockwave).
Structures tangage
La symétrie est également un facteur important dans la formation de échelles et cordes, classique ou la musique tonale étant constituée de groupes non symétriques emplacements, tels que la gamme diatonique ou l' accord majeur. Échelles ou des accords symétriques, tels que l' échelle entière de tonalité, accord augmenté ou diminué accord de septième (diminuée-septième diminuée), on dit à la direction un manque ou un sentiment de mouvement vers l'avant, sont ambigus quant à la touche centrale ou tonale, et ont une moins spécifique fonctionnalité diatonique. Cependant, des compositeurs comme Alban Berg, Béla Bartók, et George Perle ont utilisé des axes de symétrie et / ou cycles d'intervalle d'une manière analogue à touches ou non tonales tonales centres.
Perle (1992) explique "CE, DF #, [et] Eb-G, sont différentes instances du mêmeintervalle ... l'autre sorte d'identité. ..has à voir avec des axes de symétrie. CE appartient à une famille de dyades symétriquement liés comme suit: "
| Ré | RÉ # | E | Fa | F # | Sol | G # | ||||||
| Ré | C # | C | B | UN # | Un | G # |
Ainsi, en plus de faire partie de l'intervalle 4-famille, CE est également une partie de la somme-4 famille (avec C égal à 0).
| + | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||
| 2 | 1 | 0 | 11 | 10 | 9 | 8 | |||||||
| 4 | 4 | 4 | 4 | 4 | 4 | 4 |
Intervalle cycles sont symétriques et donc non-diatonique. Toutefois, un segment de sept pas de C5 (le cycle des quintes, qui sont enharmonique avec le cycle des quarts) va produire la gamme majeure diatonique. Tonales cycliques progressions dans les œuvres de compositeurs romantiques tels que Gustav Mahler et Richard Wagner constituent un lien avec les successions de pas cyclique dans la musique atonale des modernistes tels que Bartók, Alexandre Scriabine, Edgard Varèse, et l'école de Vienne. Dans le même temps, ces progressions signalent la fin de la tonalité.
La première composition élargie constamment basée sur des relations de hauteur symétriques était probablement d'Alban Berg Quartet , Op. 3 (1910). (Perle, 1990)
Équivalence
rangées de tonalité oula classe de hauteurensembles qui sontinvariantes parrétrograde sont horizontalement symétrique, sousinversion verticalement. Voir également rythme asymétrique.
Symétrie dans d'autres arts et métiers

Le concept de symétrie est appliquée à la conception d'objets de toutes formes et tailles. D'autres exemples comprennent perlage,les meubles, lespeintures de sable,entrelacs,masques,instruments de musique, et de nombreuses autres activités.
Symétrie dans l'esthétique
La relation de symétrie de l'esthétique est complexe. Certaines symétries simples, et en particulier la symétrie bilatérale, semblent être profondément ancrée dans la perception inhérente par les humains de la santé probable ou remise en forme des autres créatures vivantes, comme on peut le voir par la simple expérience de fausser un côté de l'image d'une attrayante visage et en demandant aux téléspectateurs de noter l'attractivité de l'image résultante. Par conséquent, ces symétries qui imitent la biologie ont tendance à avoir un appel innée qui entraîne à son tour une forte tendance à créer des artefacts à symétrie similaire. Il suffit d'imaginer la difficulté en essayant de commercialiser un très asymétrique voiture ou camion pour les acheteurs d'automobiles générales de comprendre la puissance de symétries d'inspiration biologique tels que la symétrie bilatérale.
Un autre appel plus subtile de symétrie est celui de la simplicité, qui à son tour a une implication de la sécurité, de la sécurité, et la familiarité. Une salle très symétrique, par exemple, est inévitablement aussi une salle dans laquelle tout ce qui sort de l'endroit ou menaçant potentiellement peuvent être identifiés facilement et rapidement. Les personnes qui ont, par exemple, grandi dans des maisons pleines de bons angles exacts et précis artefacts identiques peuvent trouver leur première expérience en séjournant dans une chambre avec aucun angle droit exactes et aucun des artefacts exactement identiques à être très inquiétante. Symétrie peut donc être une source de réconfort non seulement comme un indicateur de la santé biologique, mais aussi d'un milieu de vie sécuritaire et bien compris.
Opposé à cela est la tendance pour la symétrie excessive à être perçu comme ennuyeux ou inintéressant. Les êtres humains en particulier, ont un puissant désir d'exploiter de nouvelles opportunités ou explorer de nouvelles possibilités, et un degré excessif de symétrie peut transmettre un manque de telles opportunités.
Pourtant, une autre possibilité est que lorsque symétries deviennent trop complexe ou trop difficile, l'esprit humain a tendance à "affiner les sortir" et de les percevoir dans un autre mode: commele bruit qui transmet aucune information utile.
Enfin, les perceptions et l'appréciation des symétries dépendent également sur fond culturel. L'utilisation beaucoup plus grande des symétries géométriques complexes dans de nombreux islamiques cultures, par exemple, il est plus probable que les gens de ces cultures apprécieront ces formes d'art (ou, au contraire, à se rebeller contre eux).
Comme dans beaucoup d'activités humaines, le résultat de la convergence de nombreux facteurs tels que l'utilisation efficace de symétrie dans l'art et l'architecture est complexe, intuitive, et très dépendantes des compétences des personnes qui doivent tisser et de combiner ces facteurs dans leur propre créativité travail. Avec la texture, la couleur, la proportion, et d'autres facteurs, la symétrie est un ingrédient puissant dans une telle synthèse; il suffit d'examiner le Taj Mahal au rôle important que joue la symétrie dans la détermination de l'attrait esthétique d'un objet.
Quelques exemples de l'utilisation plus explicite des symétries dans l'art peuvent être trouvées dans l'art remarquable deMC Escher, la conception créatrice du concept mathématique d'ungroupe de fonds d'écran, et les nombreuses applications (à la fois mathématiques et le monde réel) decarrelage.
Symétrie dans les jeux et les puzzles
- Voir également jeux symétriques.
- Voirsudoku.
Jeux de société
- The Chess Collection symétrique
Symétrie dans la littérature
Voir palindrome.
Symétrie morale
- Tac au tac
- Réciprocité
- Règle D'Or
- L'empathie etsympathie
- Équilibre réfléchi

