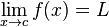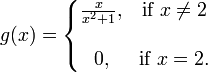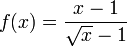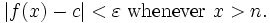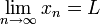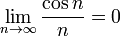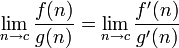Limite (mathématiques)

Saviez-vous ...

Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet a été une initiative de SOS Enfants. Parrainer un enfant de faire une réelle différence.

Le Wikibook Calcul a une page sur le thème de: Limites

En mathématiques , la notion de «limite» est utilisé pour décrire la comportement d'une fonction que son l'argument soit "se rapproche" à un moment donné, ou comme il devient arbitrairement grande; ou le comportement d'une séquence éléments s 'comme leur indice augmente indéfiniment. Les limites sont utilisées dans le calcul et les autres branches de l'analyse mathématique pour définir dérivés et la continuité.

Le concept de la "limite d'une fonction" est plus généralisée de la notion de topologique net, tandis que la limite d'une suite est étroitement liée à limite et limite directe théorie des catégories.

Limite d'une fonction

Supposons que f (x) est une fonction à valeurs réelles et c est un nombre réel . L'expression:

$\ {X lim_ \ à c} f (x) = L$

signifie que ƒ (x) peut être fait pour être aussi proche de L comme vous le souhaitez en faisant x suffisamment proche de c. Dans ce cas, nous disons que "la limite de ƒ de x, quand x tend vers c, est L". Notez que cette déclaration peut être vrai même si 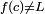$\ Scriptstyle f (c) \ L neq$ . En effet, la fonction f (x) ne doit pas même être défini au c. Deux exemples permettent d'illustrer cela.

Envisager 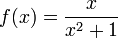$f (x) = \ frac {x} {x ^ 2 + 1}$ quand x tend 2. Dans ce cas, f (x) est définie à 2 et est égal à la limite de 0,4:

f (1,9)	f (1,99)	f (1,999)	f (2)	f (2,001)	f (2,01)	f (2,1)
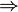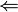0,4121	0,4012	0,4001	$\ Flèche Droite$ 0,4 $\ Leftarrow$	0,3998	0,3988	0,3882

Comme x 2 approches, ƒ (x) 0,4 approches et donc nous avons 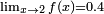$\ Scriptstyle \ {x lim_ \ 2} f (x) = 0,4$ . Dans le cas où 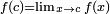$\ Scriptstyle f (c) = \ {x lim_ \ à c} f (x)$ , Ƒ est dit être continu à x = c. Mais il ne est pas toujours le cas. Envisager

$g (x) = \ \ left {\ begin {matrix} \ frac {x} {x ^ 2 + 1}, et \ mbox {if} x \ 2 ne \\ \\ 0, & \ mbox {if} x = 2. \ End {matrix} \ right.$

La limite de g (x) lorsque x tend vers 2 est de 0,4 (comme dans f (x)), mais 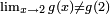$\ Scriptstyle \ {x lim_ \ 2} g (x) \ neq g (2)$ ; G ne est pas continu à x = 2.

Ou, considérons le cas où ƒ (x) ne est pas défini à x = c.

$f (x) = \ frac {x - 1} {\ sqrt {x} - 1}$

Dans ce cas, quand x tend vers 1, f (x) ne est pas définie à x = 1, mais la limite est égal à 2:

f (0,9)	f (0,99)	f (0,999)	f (1,0)	f (1,001)	f (1,01)	f (1,1)
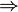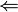1,95	1,99	1,999	$\ Flèche Droite$ undef $\ Leftarrow$	2,001	2,010	2.10

Ainsi, f (x) peut être faite arbitrairement proche de la limite de 2 x tout en faisant suffisamment assez proche de 1.

Définition formelle

Karl Weierstrass définie formellement une limite comme suit:

Soit f une fonction définie sur un intervalle ouvert contenant c (sauf peut-être au c) et laisser L un nombre réel .

$\ {X lim_ \ à c} f (x) = L$

signifie que

pour chaque réel ε> 0, il existe un réel δ> 0 tel que pour tout x avec 0 <| x - c | <δ, nous avons | f (x) - L | <ε.

La définition formelle d'une limite est parfois appelée la forme delta-epsilon, car il utilise les lettres grecques delta (δ) et epsilon (ε). L'utilisation des lettres grecques particuliers δ et ε est simplement traditionnelle; la définition serait, bien entendu, être inchangée si différentes lettres ou des symboles sont utilisés.

Attention: Il est à noter que cette définition fournit un moyen de reconnaître une limite sans fournir une façon de le calculer. Il faut souvent de trouver une limite en utilisant des procédés informels, en particulier lorsque f (x) est discontinue à c, par exemple, lorsque f est un rapport dont le dénominateur qui devient 0 à c. Il faut vérifier que le résultat répond effectivement à la définition Weierstrass dans de tels cas.

Limite d'une fonction à l'infini

Un concept lié à des limites que x tend vers un certain nombre fini est la limite quand x tend positive ou négative l'infini . Cela ne signifie pas littéralement que la différence entre x et l'infini devient faible, puisque l'infini ne est pas un nombre réel; plutôt, cela signifie que soit x croît sans lié positivement (infini positif) ou croît sans lié négativement (infini négatif).

Par exemple, considérons f (x) = 2 x / (x + 1).

f (100) = 1,9802
f (1000) = 1,9980
f (10000) = 1,9998

Comme x devient extrêmement grande, la valeur de f (x) se rapproche de 2, la valeur de f (x) peut être rendu aussi proche de 2 à souhait tout en ramassant x suffisamment grand. Dans ce cas, nous disons que la limite de f (x) quand x tend vers l'infini est 2. Dans la notation mathématique,

$\ {X lim_ \ to \ infty} f (x) = 2.$

Formellement, nous avons la définition

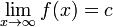$\ {X lim_ \ to \ infty} f (x) = c$ si et seulement si pour chaque ε> 0, il existe un n tel que

$| F (x) - c | <\ varepsilon \ text {} lorsque x> n.$

Notez que le n dans la définition dépend généralement de ε. Une définition similaire se applique pour 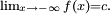$\ Scriptstyle \ {x lim_ \ à - \ infty} f (x) = c.$

Si l'on considère la domaine de f soit le longue ligne de nombre réel, alors la limite d'une fonction à l'infini peut être considéré comme un cas particulier de limite d'une fonction en un point.

Limite d'une séquence

Considérons la séquence suivante: 1,79, 1,799, 1,7999, ... Nous avons pu observer que les chiffres sont "approchent" 1.8, la limite de la séquence.

Formellement, supposons que x _1, x _2, ... est une séquence de nombres réels . Nous disons que le nombre réel L est la limite de cette séquence et nous écrivons

$\ N \ {lim_ à \ infty} x_n = L$

si et seulement si pour tout nombre réel ε> 0, il existe un nombre naturel n ₀ (qui dépendra de ε) tel que pour tout n> n ₀ nous avons | x _n - L | <ε.

Intuitivement, cela signifie que finalement tous les éléments de la séquence se rapprocher autant que nous voulons à la limite, puisque la valeur absolue | x _n - L | est la distance entre x et L _n. Non chaque séquence a une limite; si ce est le cas, nous l'appelons convergente, sinon divergentes. On peut montrer que une séquence convergente a qu'une seule limite.

La limite d'une séquence et la limite d'une fonction sont étroitement liés. D'une part, la limite d'une suite est simplement la limite à l'infini d'une fonction définie sur des nombres naturels . D'autre part, une limite d'une fonction f au point x, se il existe, est la même que la limite de la suite x _n = f (x + 1 / n).

Identités utiles

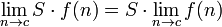$\ N \ {lim_ à c} S \ Sdot f (n) = S \ Sdot \ n \ {lim_ à c} f (n)$ , Où S est un multiplicateur scalaire.
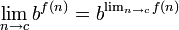$\ N \ lim_ {} b à c ^ {f (n) = b} ^ {\ {n \ lim_ à c} f (n)}$ , Où b est une constante.

Les règles suivantes ne sont valables que si les limites sur le côté droit existe et sont finies.

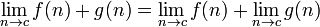
$\ N \ {lim_ à c} f (n) + g (n) = \ {n \ lim_ à c} f (n) + \ {n \ lim_ à c} g (n)$
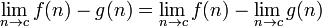
$\ N \ {lim_ à c} f (n) - g (n) = \ {n \ lim_ à c} f (n) - \ n \ {lim_ à c} g (n)$
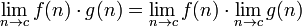
$\ N \ {lim_ à c} f (n) \ Sdot g (n) = \ {n \ lim_ à c} f (n) \ Sdot \ n \ {lim_ à c} g (n)$
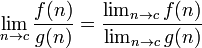$\ N \ {lim_ à c} \ frac {f (n)} {g (n)} = \ frac {\ {n \ lim_ à c} f (n)} {\ {n \ lim_ à c} g ( n)}$ , Si le dénominateur contenant la limite ne est pas égal à zéro

Si l'une des limites dans le côté droit ne est pas défini ou infini, les règles ne fonctionnent pas nécessairement.

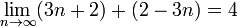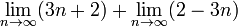Par exemple, $\ Lim_ {n \ to \ infty} (3n + 2) + (2-3n) = 4$ mais $\ Lim_ {n \ to \ infty} (3n + 2) + \ lim_ {n \ to \ infty} (2-3n)$ ne est pas défini.

Limites de l'intérêt supplémentaire

$\ N \ {lim_ à 0} \ frac {\ sin n} {n} = 1$
$\ N \ {lim_ à 0} \ frac {1 - \ cos n} {n} = 0$
$\ N \ {lim_ à \ infty} \ frac {\ sin n} {n} = 0$
$\ N \ {lim_ à \ infty} \ frac {\ cos n} {n} = 0$

la règle de l'Hôpital

Cette règle utilise dérivés et a une utilisation conditionnelle. Il ne peut être utilisé sur formes indéterminées.

$\ N \ {lim_ à c} \ frac {f (n)} {g (n)} = \ {n \ lim_ à c} \ frac {f '(n)} {g' (n)}$

Par exemple: 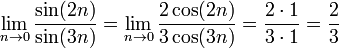$\ N \ {lim_ à 0} \ frac {\ sin (2n)} {\ sin (3n)} = \ {n \ lim_ à 0} \ frac {2 \ cos (2n)} {3 \ cos (3n) } = \ frac {2 \ Sdot 1} {3 \ Sdot 1} = \ frac {2} {3}$

Sommations

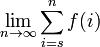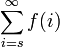
Une courte façon d'écrire la limite $\ N \ {lim_ à \ infty} \ sum_ {i = s} ^ {n} f (i)$ est $\ Sum_ {i = s} ^ {\ infty} f (i)$

Net topologique

Toutes les notions ci-dessus de la limite peut être unifiée et généralisée au arbitraire espaces topologiques en introduisant topologique filets et la définition de leurs limites. L'article sur les filets des précisions sur ce sujet.

Une alternative est la notion de limite pour filtres sur les espaces topologiques.

Limite de la théorie des catégories

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Limit_(mathematics)&oldid=189022086 "

We provide Linux to the World