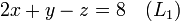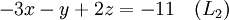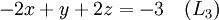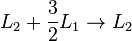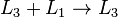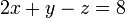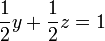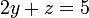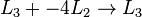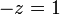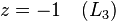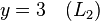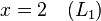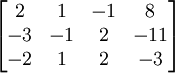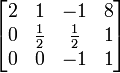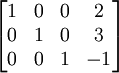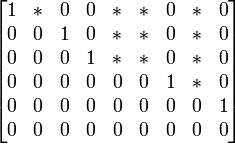Eliminação de Gauss
Sobre este escolas selecção Wikipedia
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?
Em álgebra linear , a eliminação de Gauss é um algoritmo que pode ser usado para determinar as soluções de um sistema de equações lineares , para encontrar o posto de uma matriz , e para calcular o inverso de um matriz quadrada invertível. Eliminação de Gauss é nomeado após matemático e cientista alemão Carl Friedrich Gauss .
Operações elementares de linha são utilizados em todo o algoritmo. O algoritmo tem duas partes, cada uma das quais considera as linhas da matriz, a fim. A primeira parte da matriz reduz a forma escalonada, enquanto o segundo reduz a matriz ainda mais a forma escalonada reduzida por linha. A primeira parte é suficiente para muitas aplicações.
Um algoritmo relacionado, mas menos eficiente, Eliminação de Gauss-Jordan, traz uma matriz de forma escalonada reduzida por linha em uma passagem.
História
O método de eliminação de Gauss aparece no Capítulo Oito, matrizes retangulares, do importante chinês texto matemático Jiuzhang suanshu ou Os Nove Capítulos da Arte Matemática. A sua utilização está ilustrado na dezoito problemas, com 2-5 equações. A primeira referência ao livro com esse título é datado de 179 dC, mas partes dela foram escritas logo em cerca de 150 aC.
No entanto, o método foi inventado na Europa independentemente. É nomeado após o matemático Carl Friedrich Gauss .
Resumo Algorithm
O processo de eliminação de Gauss tem duas partes. A primeira parte (frente Eliminação) reduz um dado sistema, quer ou triangular forma escalonada, ou resulta em uma equação degenerada sem solução, indicando que o sistema não tem solução. Isto é conseguido através da utilização de operações elementares de linha. A segunda etapa usos substituição de volta para encontrar a solução do sistema acima.
Dito de forma equivalente para matrizes, a primeira parte reduz uma matriz para escalonada formulário usando operações elementares de linha enquanto o segundo reduz a forma escalonada reduzida por linha, ou remar forma canônica.
Outro ponto de vista, o que acaba por ser muito útil para analisar o algoritmo, é que a eliminação de Gauss calcula um decomposição da matriz. As três operações elementares de linha utilizados na eliminação de Gauss (multiplicação de linhas, alternando linhas, e adicionar múltiplos de linhas para outras linhas) ascendem a multiplicação da matriz original com matrizes invertíveis a partir da esquerda. A primeira parte do algoritmo calcula uma LU decomposição, enquanto a segunda parte escreve a matriz original como o produto de uma matriz invertível unicamente determinada e uma reduzida matriz escalonada unicamente determinado.
Exemplo
Suponhamos que o objectivo é encontrar e descrever a solução (ões), se houver, do seguinte sistema de equações lineares :
O algoritmo é como segue: eliminar 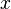 a partir de todas as equações abaixo
a partir de todas as equações abaixo 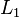 , E, em seguida, eliminar
, E, em seguida, eliminar 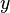 a partir de todas as equações abaixo
a partir de todas as equações abaixo 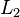 . Isto irá colocar o sistema em forma triangular. Em seguida, utilizando volta-substituição, cada amostra desconhecida pode ser resolvida para.
. Isto irá colocar o sistema em forma triangular. Em seguida, utilizando volta-substituição, cada amostra desconhecida pode ser resolvida para.
No nosso exemplo, nós eliminamos 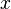 de
de 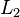 adicionando
adicionando 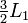 para
para 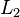 E, em seguida, eliminamos
E, em seguida, eliminamos 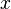 de
de 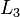 adicionando
adicionando 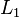 para
para 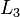 . Formalmente:
. Formalmente:
O resultado é:
Agora nós eliminamos 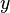 de
de 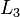 adicionando
adicionando 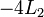 para
para 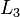 :
:
O resultado é:
Este resultado é um sistema de equações lineares em forma triangular, e assim a primeira parte do algoritmo é completa.
A segunda parte, de volta de substituição, consiste de resolver as incógnitas na ordem inversa. Assim, podemos ver facilmente que
Em seguida, 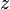 pode ser substituído em
pode ser substituído em 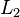 , Que pode então ser resolvido para se obter facilmente
, Que pode então ser resolvido para se obter facilmente
Em seguida, 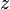 e
e 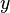 pode ser substituído em
pode ser substituído em 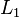 , O que pode ser resolvido para se obter
, O que pode ser resolvido para se obter
Assim, o sistema é resolvido.
Este algoritmo funciona para qualquer sistema de equações lineares. É possível que o sistema não pode ser reduzida para a forma triangular, mas ainda tem pelo menos uma solução válida: por exemplo, se 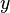 não havia ocorrido em
não havia ocorrido em 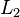 e
e 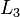 após a primeira etapa acima, o algoritmo teria sido incapaz de reduzir o sistema de forma triangular. No entanto, ele ainda teria reduzido o sistema para forma escalonada. Neste caso, o sistema não tem uma solução única, uma vez que contém pelo menos um variável livre. O conjunto da solução pode então ser expresso parametricamente (isto é, em termos de variáveis livres, de modo que, se os valores para as variáveis livres são escolhidos, uma solução será gerado).
após a primeira etapa acima, o algoritmo teria sido incapaz de reduzir o sistema de forma triangular. No entanto, ele ainda teria reduzido o sistema para forma escalonada. Neste caso, o sistema não tem uma solução única, uma vez que contém pelo menos um variável livre. O conjunto da solução pode então ser expresso parametricamente (isto é, em termos de variáveis livres, de modo que, se os valores para as variáveis livres são escolhidos, uma solução será gerado).
Na prática, não é normalmente lidar com os sistemas actuais em termos de equações, mas em vez disso faz uso do matriz aumentada (que também é adequado para manipulações de computador). Este, então, é o algoritmo Gaussian Eliminação aplicada ao matriz aumentada do sistema acima, começando com:
que, no final da primeira parte do algoritmo tem esta aparência:
Ou seja, é em forma escalonada.
No final do algoritmo, que são deixados com
Ou seja, é em forma escalonada reduzida por linha, ou forma canônica linha.
Outras aplicações
Encontrando-se o inverso de uma matriz
Supor 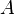 é um
é um 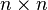 matriz e você precisa calcular o seu inverso. O
matriz e você precisa calcular o seu inverso. O 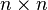 matriz de identidade é aumentada à direita
matriz de identidade é aumentada à direita 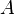 , Formando um
, Formando um 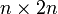 matriz (o matriz de bloco
matriz (o matriz de bloco ![B = [A, I]](../../images/142/14234.png) ). Através da aplicação de operações elementares de linha eo algoritmo de eliminação de Gauss, o bloco deixou de
). Através da aplicação de operações elementares de linha eo algoritmo de eliminação de Gauss, o bloco deixou de 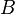 pode ser reduzida para a matriz identidade
pode ser reduzida para a matriz identidade 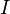 , O que deixa
, O que deixa 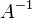 no bloco de direita
no bloco de direita 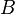 .
.
Se o algoritmo for incapaz de reduzir 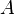 de forma triangular, em seguida
de forma triangular, em seguida 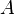 não é invertida.
não é invertida.
Na prática, a inversão de uma matriz é raramente necessária. Na maioria das vezes, é realmente a solução depois de um determinado sistema de equações lineares.
O algoritmo geral para calcular fileiras e bases
O algoritmo de eliminação de Gauss pode ser aplicado a qualquer 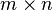 matriz
matriz 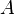 . Se conseguirmos "preso" em uma determinada coluna, passamos para a próxima coluna. Deste modo, por exemplo, alguns
. Se conseguirmos "preso" em uma determinada coluna, passamos para a próxima coluna. Deste modo, por exemplo, alguns 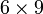 matrizes podem ser transformados em uma matriz que tem uma forma escalonada reduzida como
matrizes podem ser transformados em uma matriz que tem uma forma escalonada reduzida como
(As * 's são entradas arbitrárias). Esta matriz escalonada 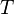 contém uma riqueza de informações sobre
contém uma riqueza de informações sobre 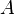 : O Ranking de
: O Ranking de 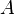 5 é uma vez que existem cinco linhas não nulos nas
5 é uma vez que existem cinco linhas não nulos nas 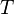 ; o espaço vectorial gerado por as colunas de
; o espaço vectorial gerado por as colunas de 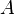 tem uma base que consiste no primeiro, terceiro, quarto, sétima e nona coluna de
tem uma base que consiste no primeiro, terceiro, quarto, sétima e nona coluna de 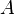 (as colunas de aqueles em
(as colunas de aqueles em 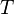 ), Eo * 's dizer-lhe como as outras colunas
), Eo * 's dizer-lhe como as outras colunas 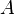 pode ser escrita como combinações lineares das colunas de base.
pode ser escrita como combinações lineares das colunas de base.
Análise
Eliminação de Gauss em uma matriz n × n requer aproximadamente 2 n 03/03 operações. Por isso, tem uma complexidade de 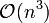 .
.
Este algoritmo pode ser utilizado em um computador para sistemas com milhares de equações e incógnitas. No entanto, o custo torna-se proibitivo para sistemas com milhões de equações. Estas grandes sistemas são geralmente resolvidos usando métodos iterativos. Existem métodos específicos para os sistemas cujos coeficientes seguem um padrão regular (ver sistema de equações lineares ).
A eliminação de Gauss pode ser realizada através de qualquer campo.
Eliminação de Gauss é numericamente estável durante dominante em diagonal ou matrizes positivo-definido. Para matrizes gerais, eliminação de Gauss é geralmente considerado estável, na prática, se você usar pivotamento parcial como descrito abaixo, mesmo que haja exemplos para os quais é instável.
Pseudocódigo
Como explicado acima, a eliminação de Gauss escreve uma dada matriz m x n Um exclusivamente como um produto de um m invertível × m matriz S e uma matriz escalonada t. Aqui, S é o produto das matrizes correspondentes às operações realizadas fileira.
O algoritmo para calcular formais 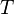 de
de 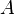 segue. Nós escrevemos
segue. Nós escrevemos ![Uma [i, j]](../../images/142/14240.png) para a entrada na linha
para a entrada na linha 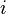 , Coluna
, Coluna 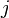 em matriz
em matriz 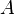 . A transformação é realizada "in place", o que significa que a matriz original
. A transformação é realizada "in place", o que significa que a matriz original 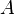 é perdida e substituída sucessivamente pela
é perdida e substituída sucessivamente pela 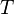 .
.
i := 1 j := 1 while (i ≤ m and j ≤ n) do Find pivot in column j, starting in row i: maxi := i for k := i+1 to m do if abs(A[k,j]) > abs(A[maxi,j]) then maxi := k end if end for if A[maxi,j] ≠ 0 then swap rows i and maxi, but do not change the value of i Now A[i,j] will contain the old value of A[maxi,j]. divide each entry in row i by A[i,j] Now A[i,j] will have the value 1. for u := i+1 to m do subtract A[u,j] * row i from row u Now A[u,j] will be 0, since A[u,j] - A[i,j] * A[u,j] = A[u,j] - 1 * A[u,j] = 0. end for i := i + 1 end if j := j + 1 end while Este algoritmo é um pouco diferente da que foi discutido anteriormente, porque antes de eliminar uma variável, esta primeira troca linhas para mover a entrada com o maior valor absoluto para a posição "pivot". Tal pivotante procedimento melhora a estabilidade numérica do algoritmo; algumas variantes também estão em uso.
A coluna actualmente a ser transformado é chamado a coluna dinâmica. Continuar a partir da esquerda para a direita, deixando a coluna de pivô ser a primeira coluna, em seguida, a segunda coluna, etc, e, finalmente, a última coluna antes da linha vertical. Para cada coluna dinâmica, fazer as duas etapas seguintes, antes de passar para a próxima coluna pivô:
- Localize o elemento diagonal na coluna pivô. Este elemento é chamado o pivô. A linha que contém o pivot é chamado a linha pivô. Divida cada elemento na linha pivô pelo pivô para obter uma nova linha de pivô com um 1 na posição de pivô.
- Obter um 0 em cada posição por baixo da posição de articulação subtraindo um múltiplo apropriado da linha de articulação de cada uma das linhas abaixo dela.
Após a conclusão deste procedimento a matriz aumentada estará em forma escalonada e pode ser resolvido por volta de substituição.