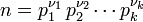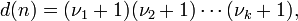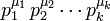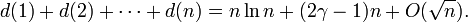Divisor
Antecedentes de las escuelas de Wikipedia
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Antes de decidir sobre el patrocinio de un niño, ¿por qué no aprender sobre diferentes obras de caridad de patrocinio primero ?
En las matemáticas , un divisor de un número entero n, también llamado un factor de n, es un número entero que divide de manera uniforme n sin dejar resto.
Explicación
Por ejemplo, 7 es un divisor de 42 porque 42/7 = 6. También decimos 42 es divisible por 7 o 42 es una múltiplo de 7 o 7 divisiones 42 o 7 es un factor de 42 y por lo general escribir 7 | 42. Por ejemplo, los divisores positivos de 42 son 1, 2, 3, 6, 7, 14, 21, 42.
En general, decimos m | n (leer: m divide n) para enteros m y n no cero si y sólo si existe un entero k tal que n = km. Por lo tanto, divisores pueden ser negativos así como positivos, aunque a menudo nos restringimos nuestra atención a divisores positivos. (Por ejemplo, hay seis divisores de cuatro, 1, 2, 4, -1, -2, -4, pero uno se suele mencionar sólo los positivos, 1, 2 y 4.)
1 y -1 dividir (son) divisores de cada número entero, todo entero (y su negación) es un divisor de sí mismo, y todo entero es un divisor de 0, excepto por convención 0 en sí (véase también división por cero). Los números divisibles por 2 se llaman incluso y los números no divisibles por 2 son llamados impar.
Un divisor de n que no es 1, -1, n o - n (que son divisores triviales) se conoce como un divisor no trivial; números con divisores no triviales se conocen como números compuestos, mientras que los números primos no tienen divisores no triviales.
El nombre proviene de la aritmética operación de división : si a / b = c, entonces a es el dividendo , el divisor b, y c la cociente.
Hay propiedades que le permiten a uno a reconocer ciertas divisores de un número de dígitos del número.
Otras nociones y hechos
 | El wikilibro El libro de matemáticas pruebas tiene una página sobre el tema de: Las pruebas de las propiedades de divisibilidad |
Algunas reglas elementales:
- Si a | b y a | c, entonces a | (b + c), de hecho, a | + mb (NC) para todos los enteros m, n.
- Si a | b & b | c, entonces a | c. ( transitiva relación)
- Si a | b & b | a, entonces a = b o a = - b.
La siguiente propiedad es importante:
- Si a | bc, y mcd (a, b) = 1, entonces a | c. ( Lema de Euclides)
Un divisor positivo de n que es diferente de n se llama un divisor adecuado (o parte alícuota) de n. (Un número que no uniformemente dividir n, pero deja un resto, se llama una porción alicuanta parte de n.)
Un entero n> 1 cuyo único adecuado divisor es 1 se llama un número primo . De manera equivalente, se diría que un número primo es aquel que tiene exactamente dos factores: 1 y sí mismo.
Cualquier divisor positivo de n es un producto de divisores primos de n elevado a alguna potencia. Esto es una consecuencia del teorema fundamental de la aritmética .
Si un número es igual a la suma de sus divisores apropiados, se dice que es un número perfecto . Números menores que la suma de sus divisores apropiados se dice que son abundante; mientras que los números mayores de esa suma se dice que son deficiente.
El número total de divisores positivos de n es una multiplicativo función d (n) (por ejemplo, d (42) = 8 = 2 x 2 x 2 = d (2) × d (3) × d (7)). La suma de los divisores positivos de n es otra función σ multiplicativo (n) (por ejemplo, σ (42) = 96 = 3 x 4 x 8 = σ (2) × σ (3) × σ (7)). Ambas funciones son ejemplos de funciones divisor.
Si el descomposición en factores primos de n viene dada por
entonces el número de divisores positivos de n es
y cada uno de los divisores tiene la forma
donde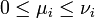 
para cada 
.
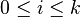Se puede demostrar que
Una interpretación de este resultado es que un número entero positivo elegido al azar n tiene un número esperado de divisores de alrededor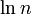 
.
La divisibilidad de los números
La relación de divisibilidad convierte el conjunto N de no negativos enteros en un parcialmente ordenado conjunto, de hecho, en un completar retículo distributivo. El mayor elemento de esta celosía es 0 y el más pequeño es 1. La operación se reúnen ^ está dada por el máximo común divisor y la operación de combinación v por el minimo común multiplo. Esta celosía es isomorfo al dual de la celosía de subgrupos de la infinita grupo cíclico Z .
Generalización
Uno puede hablar sobre el concepto de divisibilidad en cualquier dominio integral. Por favor, ver ese artículo para las definiciones de dicha configuración.
