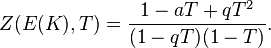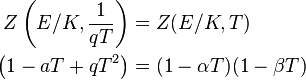Curva elíptica
Antecedentes
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

En matemáticas , una curva elíptica es una liso, descriptivo curva algebraica de un género, en el que hay un punto O especificado. Una curva elíptica es de hecho una abelian variedad - es decir, que tiene una multiplicación definida algebraicamente, con respecto a la que es (necesariamente conmutativa ) grupo - O y sirve como el elemento de identidad. A menudo, la curva de sí mismo, sin O especifica, que se llama una curva elíptica.
Cualquier curva elíptica puede ser escrito como una curva plana algebraica definida por una ecuación de la forma:
que es no singular; es decir, su gráfica no tiene cúspides o auto-intersecciones. (Cuando el característica del campo coeficiente es igual a 2 o 3, la ecuación anterior no es suficiente en general a comprender todos los no-singular curvas cúbicas; ver más abajo para una definición más precisa.) El punto O es en realidad el " punto en el infinito "en el plano proyectivo.
Si y 2 = P (x), donde P es cualquier polinomio de grado tres en x sin raíces repetidas, a continuación, se obtiene una curva plana no singular de un género, que es por lo tanto también una curva elíptica. Si P tiene grado cuatro y es squarefree esta ecuación de nuevo describe una curva plana de género uno; sin embargo, no tiene más remedio natural del elemento de identidad. Más en general, cualquier curva algebraica de género uno, por ejemplo de la intersección de dos superficies cuadráticas incrustados en tres dimensiones del espacio proyectivo, se llama una curva elíptica, siempre que tenga al menos un punto racional.
Usando la teoría de la funciones elípticas, se puede demostrar que las curvas elípticas definidas en los números complejos corresponden a embeddings del toro en el plano proyectivo complejo. El toro es también un grupo abeliano, y de hecho esta correspondencia es también una isomorfismo grupo.
Las curvas elípticas son especialmente importantes en la teoría de números , y constituyen un área importante de la investigación en curso; por ejemplo, que se utilizaron en la prueba, por Andrew Wiles (asistido por Richard Taylor), del último teorema de Fermat . También encuentran aplicaciones en criptografía (ver el artículo criptografía de curva elíptica) y factorización de enteros.
Una curva elíptica no es una elipse : ver integral elíptica para el origen del término. Topológicamente, una curva elíptica es un toro .
Curvas elípticas sobre los números reales
Aunque la definición formal de una curva elíptica es bastante técnico y requiere algo de experiencia en geometría algebraica, es posible describir algunas características de las curvas elípticas sobre los números reales utilizando única escuela secundaria de álgebra y geometría .
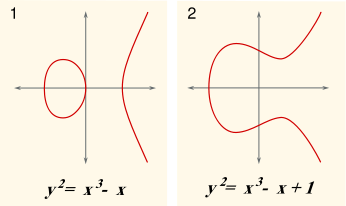
En este contexto, una curva elíptica es una curva plana definida por una ecuación de la forma
donde a y b son números reales. Este tipo de ecuación se llama una ecuación de Weierstrass.
La definición de curva elíptica también requiere que la curva sea no singular. Geométricamente, esto significa que el gráfico no tiene cúspides, auto-intersecciones o puntos aislados. Algebraicamente, esto implica el cálculo de la discriminante
La curva es no singular si y sólo si el discriminante no es igual a cero. (Aunque el factor -16 parece irrelevante aquí, resulta ser conveniente en un estudio más avanzado de curvas elípticas.)
El (real) gráfico de una curva no singular tiene dos componentes si su discriminante es positivo, y uno de los componentes si es negativo. Por ejemplo, en los gráficos mostrados en la figura de la derecha, el discriminante en el primer caso es 64, y en el segundo caso es -368.
La ley de grupo
Mediante la adición de un "punto en el infinito", se obtiene la versión proyectiva de esta curva. Si P y Q son dos puntos de la curva, entonces podemos describir de forma exclusiva un tercer punto que es la intersección de la curva con la línea a través de P y Q. Si la línea es tangente a la curva en un punto, entonces ese punto se cuenta dos veces; y si la línea es paralela a la eje y, se define el tercer punto como el punto "en el infinito". Exactamente una de estas condiciones, entonces vale para cualquier par de puntos en una curva elíptica.
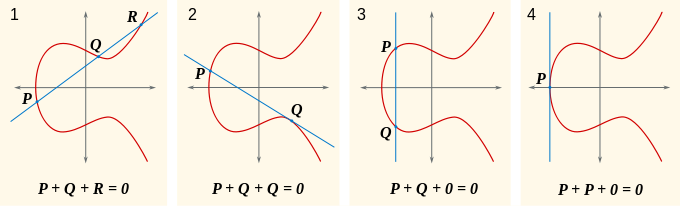
A continuación, es posible introducir una operación de grupo , +, en la curva con las siguientes propiedades: consideramos el punto en el infinito para ser 0, la identidad de grupo; y si una línea recta corta a la curva en los puntos P, Q y R, entonces se requiere que P + Q + R = 0 en el grupo. Se puede comprobar que esta gira la curva en un grupo abeliano, y por lo tanto en un variedad abeliana. Se puede demostrar que el conjunto de K - puntos racionales (incluido el punto en el infinito) forma un subgrupo de este grupo. Si la curva se denota por E, entonces este subgrupo se escribe a menudo como E (K).
El grupo de arriba puede ser descrito algebraicamente así como geométricamente. Dada la curva y 2 = x 3 - píxeles - q sobre el campo K (cuyo característica asumimos ser ni 2 ni 3), y los puntos P = (x P, y P) y Q = (x Q, y Q) en la curva, asumen primero que x P x Q ≠. Sea s la pendiente de la línea que contiene P y Q; es decir, s = (y P - y Q) / (x P - x Q). Desde K es un campo, s está bien definido. Entonces podemos definir R = P + Q = (x R, -y R) por
Si x = P x Q (tercero y cuarto paneles superiores), entonces hay dos opciones: si Y = P - y Q, incluyendo el caso en el que P y Q = y = 0, entonces la suma se define como 0; Por lo tanto, el inverso de cada punto de la curva se encuentra al reflejar a través de la eje x. Si y P = y Q ≠ 0 (segundo panel), entonces R = P + P = 2 P = (x R, -y R) está dada por
Curvas elípticas sobre los números complejos
La formulación de las curvas elípticas como la incorporación de un toro en el complejo plano proyectivo sigue naturalmente de una curiosa propiedad de Funciones elípticas de Weierstrass. Estas funciones y su primera derivada están relacionadas por la fórmula
Aquí, g 2 y 3 g son constantes; 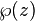 es la función elíptica de Weierstrass y
es la función elíptica de Weierstrass y 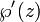 su derivado. Debe quedar claro que esta relación es en la forma de una curva elíptica (a través de los números complejos ). Las funciones de Weierstrass son doblemente periódica; es decir, que son periódicas con respecto a una celosía Λ; en esencia, las funciones de Weierstrass se definen de forma natural en un toro T = C / Λ. Este toro se puede incrustar en el complejo plano proyectivo mediante el mapa
su derivado. Debe quedar claro que esta relación es en la forma de una curva elíptica (a través de los números complejos ). Las funciones de Weierstrass son doblemente periódica; es decir, que son periódicas con respecto a una celosía Λ; en esencia, las funciones de Weierstrass se definen de forma natural en un toro T = C / Λ. Este toro se puede incrustar en el complejo plano proyectivo mediante el mapa
Este mapa es una isomorfismo grupo, llevando a la estructura del grupo natural del toro en el plano proyectivo. También es un isomorfismo de las superficies de Riemann , por lo topológicamente, una curva elíptica dada se parece a un toro. Si la celosía Λ está relacionada por la multiplicación por un número complejo distinto de cero c a una celosía Λ c, entonces las curvas correspondientes son isomorfos. Clases de isomorfismo de curvas elípticas son especificados por el j-invariante.
Las clases de isomorfismo se pueden entender de una manera más simple también. Las constantes g 2 y 3 g, llamado invariantes modulares, se determinan de forma única por la red, es decir, por la estructura del toro. Sin embargo, forman los números complejos la cuerpo de descomposición de polinomios con coeficientes reales, por lo que la curva elíptica se puede escribir como
Uno encuentra que
y
de manera que la discriminante es modular
Aquí, λ se llama a veces la función lambda modular.
Tenga en cuenta que la uniformización teorema implica que cada compacta superficie de Riemann de género puede ser representado como un toro.
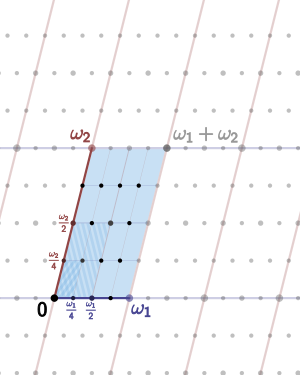
Esto también permite una fácil comprensión de la puntos de torsión en una curva elíptica: si el Λ celosía es atravesado por los períodos fundamentales ω 1 y ω 2, luego la N -torsion puntos son las (clases de equivalencia de) puntos de la forma 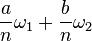 , Para a y b enteros en el rango de 0 a n -1.
, Para a y b enteros en el rango de 0 a n -1.
A través de los números complejos, cada curva elíptica tiene nueve puntos de inflexión. Cada línea a través de dos de estos puntos también pasa a través de un tercer punto de inflexión; los nueve puntos y 12 líneas formadas de esta manera forman una realización de la Configuración Hesse.
Curvas elípticas sobre los números racionales
Una curva E definida sobre el campo de los números racionales también se define sobre el campo de los números reales, por lo tanto la ley de adición (de puntos con coordenadas reales) por el método tangente y secante puede ser aplicado a E. Las fórmulas explícitas demostrar que la suma de dos puntos P y Q con coordenadas racionales tiene coordenadas racionales de nuevo, ya que la línea que une P y Q tiene coeficientes racionales. De esta manera, una muestra que el conjunto de puntos racionales de E forma un subgrupo del grupo de puntos reales de E. Como este grupo, es una grupo abeliano, es decir, P + Q = Q + P.
La estructura de puntos racionales
El resultado más importante es que todos los puntos pueden ser construidos por el método de tangentes y secantes que empiezan con un número finito de puntos. Más precisamente, la Mordell-Weil teorema establece que el grupo E (Q) es un generación finita (abeliano) grupo. Por el teorema fundamental de los grupos abelianos finitamente generados, por lo tanto es una suma directa finita de copias de Z y grupos cíclicos finitos.
La prueba de que el teorema se basa en dos principios: en primer lugar, una muestra que para cualquier entero m> 1, el grupo cociente E (Q) / Me (Q) es finito (débil teorema de Mordell-Weil). En segundo lugar, la introducción de una función de la altura h sobre los puntos racional E (Q) definida por h (P 0) = 0 y h (P) = log max (| p |, | q |) si P (desigual hasta el punto en el infinito P 0) tiene como abscisa el número racional x = p / q (con coprimero p y q). Esta función altura h tiene la propiedad de que h (MP) crece más o menos como la plaza de m. Por otra parte, sólo un número finito de puntos racionales con menor altura que las hay constante sobre E.
La prueba del teorema es por lo tanto una variante del método de descenso infinito y se basa en la aplicación repetida de Divisiones euclidianas en E: sea P ∈ E (Q) sea un punto racional en la curva, la escritura P como la suma 1 + 2 P Q 1, donde Q 1 es un representant fijo de P en E (Q) / 2 (E Q ), la altura de P 1 es de aproximadamente 1/4 de la de P (de manera más general, la sustitución de 2 por cualquier m> 1, y 1/4 por 1 / m 2). Rehacer la misma con P 1, es decir P = 1 2 2 P + Q 2, entonces P = 2 2 3 P + Q 3, etc. finalmente expresa P como una combinación lineal integral de puntos I y Q de los puntos cuya la altura está limitada por una constante fija elegido de antemano: por la débil teorema de Mordell-Weil y la segunda propiedad de la función de la altura P está así expresada como una combinación lineal integral de un número finito de puntos fijos.
Hasta el momento, el teorema no es efectivo ya que no hay procedimiento general conocida para determinar los representants de E (Q) / Me (Q).
La rango de E (Q), que es el número de copias de Z en E (Q) o, equivalentemente, el número de puntos independientes de orden infinito, se llama el rango de E. La Birch y Swinnerton-Dyer conjetura se ocupa de determinar el rango. Uno conjeturas que puede ser arbitrariamente grande, incluso si sólo se conocen ejemplos con relativamente pequeño rango. La curva elíptica con mayor rango conocido es exactamente
- y 2 + xy = x 3 − 26 175 960 092 705 884 096 311 701 787 701 203 903 556 438 969 515 x + 51 069 381 476 131 486 489 742 177 100 373 772 089 779 103 253 890 567 848 326 .
Tiene rango 18, que se encuentra por Noam Elkies en 2006. Curvas de rango, al menos 28 son conocidos, pero su rango no se conoce con exactitud.
En cuanto a los grupos que constituyen el de torsión subgrupo de E (Q), es uno de los 15 siguientes grupos (un teorema debido a que se conoce el subgrupo de torsión de E (Q) la siguiente Barry Mazur): Z / N Z para N = 1, 2, ..., 10, o 12, o Z / Z 2 × Z / Z 2 N con N = 1, 2, 3, 4. Ejemplos para cada caso son conocidos . Por otra parte, las curvas elípticas, cuyos grupos Mordell-Weil sobre Q tienen los mismos grupos de torsión pertenecen a una familia parametrizada.
La conjetura de Birch y Swinnerton-Dyer
La Conjetura de Birch y Swinnerton-Dyer (BSD) es uno de los Problemas del Milenio de las Instituto Clay de Matemáticas. La conjetura se basa en objetos de análisis y aritméticos definidos por la curva elíptica en cuestión.
En el lado analítico, un ingrediente importante es una función de una variable compleja, L, la Función zeta de Hasse-Weil de E sobre Q. Esta función es una variante de la Función zeta de Riemann y Dirichlet L-funciones. Se define como una Producto de Euler, con un factor para cada número primo p.
Para una curva E sobre Q dada por una ecuación mínimo
con coeficientes enteros a i, reduciendo los coeficientes modulo p define una curva elíptica sobre el finito campo F p (excepto para un número finito de números primos p, donde la curva tiene una reducida singularidad y por lo tanto deja de ser elíptica, en cuyo caso E se dice que es de mala reducción en p).
La función zeta de una curva elíptica sobre un campo finito F p es, en cierto sentido, un función de generación de montaje de la información del número de puntos de E con valores en el finita extensiones de campo de F p, F p n. Se da,
La suma interior de la exponencial se asemeja el desarrollo del logaritmo y, de hecho, la función zeta así definido es una función racional:
La función zeta de Hasse-Weil de E sobre Q se define entonces mediante la recopilación de esta información, para todos los primos p. Se define por
donde ε (p) = 1 si E tiene buena reducción en p y 0 en otro caso (en cuyo caso una p se define de manera diferente a la anterior).
Este producto converge para 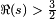 solamente. La conjetura de Hasse afirma que la función * L admite un continuación analítica al conjunto plano complejo y satisface una ecuación funcional relativa, para cualquier s, L (E, S) para L (E, 2- s). En 1999 se demostró que ser una consecuencia de la prueba de la conjetura de Shimura-Taniyama-Weil, que afirma que cada curva elíptica sobre Q es una curva modular, lo que implica que su L -Función es la -Función L de una forma modular cuya continuación analítica se conoce.
solamente. La conjetura de Hasse afirma que la función * L admite un continuación analítica al conjunto plano complejo y satisface una ecuación funcional relativa, para cualquier s, L (E, S) para L (E, 2- s). En 1999 se demostró que ser una consecuencia de la prueba de la conjetura de Shimura-Taniyama-Weil, que afirma que cada curva elíptica sobre Q es una curva modular, lo que implica que su L -Función es la -Función L de una forma modular cuya continuación analítica se conoce.
Por lo tanto, se puede hablar de los valores de L (E, s) en cualquier número complejo s. La conjetura de Birch-Swinnerton-Dyer relaciona la aritmética de la curva con el comportamiento de su L -function en s = 1. Más precisamente, se afirma que el orden de la función * L a s = 1 es igual al rango de E y predice la líder término de la serie de Laurent L (E, s) en ese punto en términos de varias cantidades unidos a la curva elíptica.
Al igual que el Hipótesis de Riemann, esta conjetura tiene múltiples consecuencias, incluidos los dos siguientes:
- Sea n un extraño entero libre de cuadrados. Suponiendo que la conjetura de Birch y Swinnerton-Dyer, n es el área de un triángulo rectángulo con longitudes de los lados racionales (un número congruente) si y sólo si el número de tripletes de números enteros (x, y, z) que satisface
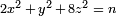 es dos veces el número de triples satisfacer
es dos veces el número de triples satisfacer 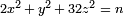 . Esta declaración, debido a Tunnell, está relacionado con el hecho de que n es un número congruente si y sólo si la curva elíptica
. Esta declaración, debido a Tunnell, está relacionado con el hecho de que n es un número congruente si y sólo si la curva elíptica 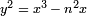 tiene un punto racional de orden infinito (por lo tanto, bajo la conjetura de Birch y Swinnerton-Dyer, su L -function tiene un cero en 1). El interés en esta declaración es que la condición se verifica fácilmente.
tiene un punto racional de orden infinito (por lo tanto, bajo la conjetura de Birch y Swinnerton-Dyer, su L -function tiene un cero en 1). El interés en esta declaración es que la condición se verifica fácilmente. - En una dirección diferente, ciertos métodos analíticos permiten una estimación de la orden de cero en el centro de la franja crítica de las familias de -Funciones L. Admitiendo la conjetura de BSD, estas estimaciones corresponden a la información sobre el rango de familias de curvas elípticas en cuestión. Por ejemplo ,: suponer la generalizada hipótesis de Riemann y la conjetura de BSD, el rango promedio de curvas dada por
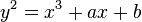 es menor que 2.
es menor que 2.
El teorema de la modularidad y su aplicación en el último teorema de Fermat
El teorema de la modularidad, una vez conocido como la conjetura de Taniyama-Shimura-Weil, establece que cada curva elíptica E sobre Q es un curva modular, es decir, su función zeta Hasse-Weil es la -Función L de una forma modular de peso 2 y el nivel N, donde N es el conductor de E (un entero divisible por los mismos números primos como el discriminante de E, Δ (E).) En otras palabras, si, por 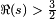 , Se escribe la función * L en forma
, Se escribe la función * L en forma
la expresion 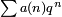 , Donde q = exp (iz 2π) define un modular parabólica NEWFORM de peso 2 y nivel N. Para los números primos ℓ no dividir N, el coeficiente
, Donde q = exp (iz 2π) define un modular parabólica NEWFORM de peso 2 y nivel N. Para los números primos ℓ no dividir N, el coeficiente 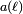 de la forma es igual a ℓ - el número de soluciones de la ecuación mínimo de la curva de ℓ módulo.
de la forma es igual a ℓ - el número de soluciones de la ecuación mínimo de la curva de ℓ módulo.
Por ejemplo, para la curva elíptica 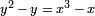 con discriminante (y director) 37, se asocia la forma
con discriminante (y director) 37, se asocia la forma 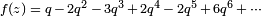 , Donde
, Donde 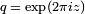 . Para números primos ℓ distintas de 37, se puede verificar la propiedad sobre los coeficientes. Así, por ℓ = 3, las soluciones de la ecuación de módulo 3 son (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , y como
. Para números primos ℓ distintas de 37, se puede verificar la propiedad sobre los coeficientes. Así, por ℓ = 3, las soluciones de la ecuación de módulo 3 son (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , y como 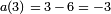 .
.
La conjetura, que se remonta a los años cincuenta, se ha demostrado por completo en 1999 utilizando ideas de Andrew Wiles, que ya demostró en 1994 por una gran familia de curvas elípticas.
Existen varias formulaciones de la conjetura. Demostrando que son equivalentes es difícil y fue un tema central de la teoría de números en la segunda mitad del siglo 20. La modularidad de una curva elíptica E de conductor N puede expresarse también diciendo que no es un no constante mapa racional definida sobre Q, a partir de la curva modular 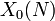 a E. En particular, los puntos de E pueden ser parametrizada por funciones modulares.
a E. En particular, los puntos de E pueden ser parametrizada por funciones modulares.
Por ejemplo, una parametrización modular de la curva de 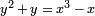 es dado por
es dado por
donde, como antes, q = exp (iz 2π). Las funciones x (z) e y (z) son modulares de peso 0 y el nivel 37; en otras palabras, son meromórfica, que se define en el semiplano superior 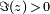 y satisfacer
y satisfacer 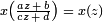 y del mismo modo para y (z) para todos los números enteros a, b, c, d con ad - bc = 1 y 37 | c.
y del mismo modo para y (z) para todos los números enteros a, b, c, d con ad - bc = 1 y 37 | c.
Otra formulación depende de la comparación de Representaciones de Galois unidos por una parte a las curvas elípticas, y por otro lado a las formas modulares. La última formulación se ha utilizado en la prueba de la conjetura. Tratar con el nivel de las formas (y la conexión con el conductor de la curva) es particularmente delicada.
La aplicación más espectacular de la conjetura es la prueba del último teorema de Fermat (FLT). Supongamos que para un primo p> 5, la ecuación de Fermat
tiene una solución con números enteros distintos de cero, por lo tanto, un contra-ejemplo para FLT. Entonces la curva elíptica
de discriminante 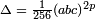 no puede ser modular. Por lo tanto, la prueba de la conjetura de Taniyama-Shimura-Weil para esta familia de curvas elípticas (llamadas curvas Hellegouarch-Frey) implica la FLT. La prueba de la relación entre estas dos declaraciones, basado en una idea de Gerhard Frey (1985), es difícil y técnico. Fue establecido por Kenneth Ribet en 1987.
no puede ser modular. Por lo tanto, la prueba de la conjetura de Taniyama-Shimura-Weil para esta familia de curvas elípticas (llamadas curvas Hellegouarch-Frey) implica la FLT. La prueba de la relación entre estas dos declaraciones, basado en una idea de Gerhard Frey (1985), es difícil y técnico. Fue establecido por Kenneth Ribet en 1987.
Puntos Integral
Esta sección se refiere a los puntos P = (x, y) de E tal que x es un número entero. El siguiente teorema es debido a CL Siegel: el conjunto de puntos P = (x, y) de E (Q) de tal manera que x es integral es finita. Este teorema se puede generalizar a puntos cuyas coordenadas x tiene un denominador divisible solamente por un conjunto finito fijo de números primos.
El teorema se puede formular de manera eficaz. Por ejemplo, si la ecuación de Weierstrass de E tiene coeficientes enteros delimitadas por una constante H, las coordenadas (x, y) de un punto de E con tanto x como número entero y satisfacer:
Por ejemplo, la ecuación 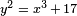 tiene ocho soluciones integrales con y> 0:
tiene ocho soluciones integrales con y> 0:
- (X, y) = (1,4), (2,3), (2,5), (4,9), (8,23), (43.282), (52.375), (5 234, 378 661).
Como otro ejemplo, La ecuación de Ljunggren, una curva cuya forma Weierstrass es y2 = x 3-2 x, tiene sólo cuatro soluciones con y ≥ 0:
- (X, y) = (0,0), (1,1), (2, 2), (338,6214).
La generalización de los campos de número
Muchos de los resultados anteriores siguen siendo válidas cuando el campo de la definición de E es un campo de número, es decir, un finito extensión de campo de la Q. En particular, el grupo E (K) de K puntos -racional de una curva elíptica E definida sobre K es de generación finita, que generaliza el teorema de Mordell-Weil anteriormente. Un teorema debido a Loïc Merel muestra que para un entero dado d, hay ( hasta el isomorfismo) sólo un número finito de grupos que pueden ocurrir como los grupos de torsión de E (K) de una curva elíptica definida sobre un cuerpo K número de grado d. Más precisamente, hay un número B (d) tal que para cualquier curva elíptica E definida sobre un campo de número K de grado d, cualquier punto de torsión de E (K) es de ordenar menos de B (d). El teorema es eficaz: para d> 1, si un punto de torsión es de orden p, con p primo, entonces 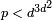 .
.
En cuanto a los puntos integrales, el teorema de Siegel generaliza a lo siguiente: sea E una curva elíptica definida sobre un campo de número K, x e y la Weierstrass coordina. Entonces los puntos de E (K) cuya coordenada x está en el anillo de los enteros O K es finito.
Las propiedades de la función zeta de Hasse-Weil y la Conjetura de Birch y Swinnerton-Dyer también pueden extenderse a esta situación más general.
Curvas elípticas sobre un campo general
Las curvas elípticas pueden definirse sobre cualquier campo K; la definición formal de una curva elíptica es una curva algebraica proyectiva no singular sobre K con género 1 con un punto dado definida sobre K.
Si el característico de K no es ni 2 ni 3, entonces cada curva elíptica sobre K se puede escribir en la forma
donde p y q son elementos de K tal que el derecho polinomio lado x 3 - píxeles - q no tiene ningún raíces dobles. Si la característica es 2 o 3, a continuación, más términos deben mantenerse: en la característica 3, la ecuación más general es de la forma
para las constantes arbitrarias 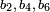 de tal manera que el polinomio en el lado de la mano derecha tiene raíces distintas (la notación es elegido por razones históricas). En característica 2, aunque esta cantidad no es posible, y la ecuación más general es
de tal manera que el polinomio en el lado de la mano derecha tiene raíces distintas (la notación es elegido por razones históricas). En característica 2, aunque esta cantidad no es posible, y la ecuación más general es
a condición de que la variedad que define es no singular. Si característica no fuera una obstrucción, cada ecuación se reduciría a los anteriores por un cambio adecuado de variables.
Una típicamente toma la curva para el conjunto de todos los puntos (x, y) que satisfacen la ecuación anterior y tal que ambos X e Y son los elementos de la clausura algebraica de K. Puntos de la curva cuyas coordenadas ambos pertenecen a K son llamados K puntos -racional.
Isogenia
Sea E y D sea curvas elípticas sobre un cuerpo k. Un isogenia entre E y D es una finito morfismo f: E → D de variedades que conserva puntos de base (en otras palabras, MAPAS El punto dado de E a la de D).
Las dos curvas se llaman isogenous si hay un isogenia entre ellos. Esta es una relación de equivalencia , la simetría se debe a la existencia de la dual isogenia. Cada isogenia es un algebraica homomorfismo y por lo tanto induce homomorfismos de los grupos de las curvas elípticas de puntos -valued k.
Las curvas elípticas sobre campos finitos
 .
. Sea K = F q sea el campo finito con elementos Q y E una curva elíptica definida sobre K. Mientras que la precisa número de puntos racionales de una curva elíptica E sobre K es en general bastante difícil de calcular, El teorema de Hasse en curvas elípticas nos da, incluido el punto en el infinito, la siguiente estimación:
En otras palabras, el número de puntos de la curva crece más o menos como el número de elementos en el campo. Este hecho puede ser entendido y demostrado con la ayuda de alguna teoría general; ver función zeta local Cohomología Étale.
 .
. El conjunto de puntos de E (F q) es un grupo abeliano finito. Siempre es cíclico o el producto de dos grupos cíclicos. Por ejemplo, la curva definida por
sobre F 71 tiene 72 puntos (71 puntos incluyendo afines (0,0) y uno punto en el infinito) sobre este campo, cuya estructura de grupo viene dado por Z / 2 Z × Z / Z 36. El número de puntos en una curva específica se puede calcular con El algoritmo de Schoof.
El estudio de la curva sobre el extensiones de campo de F q es facilitada por la introducción de la función zeta local del E sobre F q, definido por una serie de producción (véase también más arriba)
donde el campo K n es el (único) la extensión de K = F q de grado n (es decir, 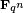 ). La función zeta es una función racional en T. Hay un número entero tal que una
). La función zeta es una función racional en T. Hay un número entero tal que una
Por otra parte,
con números complejos α, β de valor absoluto 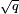 . Este resultado es un caso especial de la Conjeturas de Weil. Por ejemplo, la función zeta de
. Este resultado es un caso especial de la Conjeturas de Weil. Por ejemplo, la función zeta de 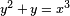 sobre el campo F 2 está dada por
sobre el campo F 2 está dada por 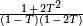 ya que la curva tiene
ya que la curva tiene 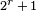 (
( 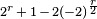 ) Puntos por encima
) Puntos por encima 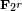 Si r es impar (incluso, respectivamente).
Si r es impar (incluso, respectivamente).

 .
. La Sato-Tate conjetura es una afirmación acerca de cómo el término de error 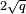 en el teorema de Hasse varía con los diferentes números primos q, si se toma una curva elíptica E sobre Q y la reduce modulo q. Fue probado (para casi todas esas curvas) en 2006 debido a los resultados de Taylor, Harris y Shepherd-Barron, y dice que los términos de error se equidistributed.
en el teorema de Hasse varía con los diferentes números primos q, si se toma una curva elíptica E sobre Q y la reduce modulo q. Fue probado (para casi todas esas curvas) en 2006 debido a los resultados de Taylor, Harris y Shepherd-Barron, y dice que los términos de error se equidistributed.
Las curvas elípticas sobre campos finitos se aplican sobre todo en la criptografía y la factorización de grandes números enteros. Estos algoritmos menudo hacen uso de la estructura del grupo en los puntos de E. Algoritmos que son aplicables a grupos generales, por ejemplo el grupo de elementos invertibles en campos finitos,  , Por lo tanto se puede aplicar al grupo de puntos sobre una curva elíptica. Por ejemplo, el logaritmo discreto es un algoritmo tal. El interés en esto es que la elección de una curva elíptica permite una mayor flexibilidad de elegir q (y por lo tanto el grupo de unidades en F q). Además, la estructura del grupo de curvas elípticas es generalmente más complicado.
, Por lo tanto se puede aplicar al grupo de puntos sobre una curva elíptica. Por ejemplo, el logaritmo discreto es un algoritmo tal. El interés en esto es que la elección de una curva elíptica permite una mayor flexibilidad de elegir q (y por lo tanto el grupo de unidades en F q). Además, la estructura del grupo de curvas elípticas es generalmente más complicado.
Los algoritmos que utilizan curvas elípticas
Las curvas elípticas sobre campos finitos se utilizan en algunos criptográficos aplicaciones, así como para factorización de enteros. Típicamente, la idea general en estas aplicaciones es que un conocido algoritmo que hace uso de ciertos grupos finitos se reescribe para utilizar los grupos de puntos racionales de curvas elípticas. Para más información, véase también:
- Criptografía de curva elíptica
- ECDSA
- Lenstra curva elíptica factorización
- Curva elíptica primality proving
Representaciones alternativas de curvas elípticas
- Curva de Hesse
- Curva de Edwards
- Curva de Twisted
- Twisted curva de Hesse
- Curva Twisted Edwards
- Curva Doche-Icart-Kohel duplicación orientada
- Curva Doche-Icart-Kohel Triplicar orientada
- Curva Jacobian
- Curva de Montgomery

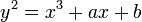
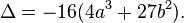

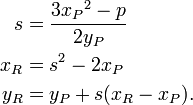
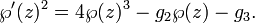
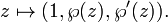
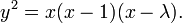
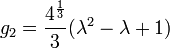
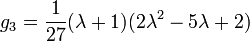
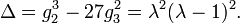
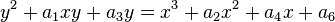
![Z (E (\ mathbf {F} _p)) = \ exp \ left (\ sum \ mathrm {} tarjeta \ left [E ({\ mathbf F} _ {p ^ n}) \ right] \ frac {T ^ n} {n} \ right).](../../images/1230/123094.png)

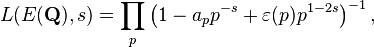
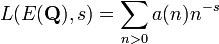
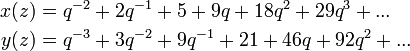
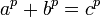

![\ Max (| x |, | y |) <\ exp \ left (\ left [10 ^ 6 H \ right] ^ {{10} ^ 6} \ right).](../../images/1231/123117.png)
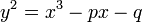
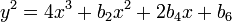
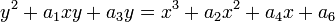
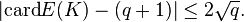
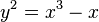
![Z (E (K), t) \ equiv \ exp \ left (\ sum_ {n = 1} ^ {\ infty} \ mathrm {tarjeta} \ left [E (k_n) \ right] {T ^ n \ over n } \ right)](../../images/1231/123137.png)