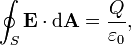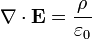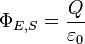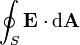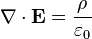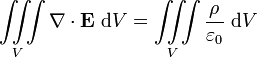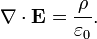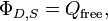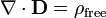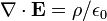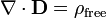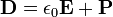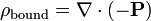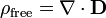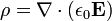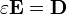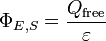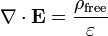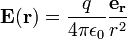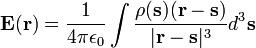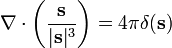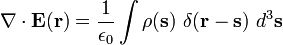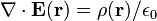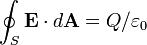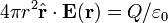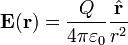La ley de Gauss

Temas relacionados: Electricidad y Electrónica

Antecedentes

SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

Electromagnetismo

Electricidad Magnetismo
Electrostática Carga eléctrica Electricidad estática Campo eléctrico Conductor Aislante Triboelectricidad La descarga electrostática Inducción La ley de Coulomb La ley de Gauss Flujo eléctrico / energía potencial Momento dipolar eléctrico Polarización eléctrica
Magnetoestática La ley de Ampère Campo magnético Magnetización Flujo magnético Ley de Biot-Savart Momento dipolar magnético La ley de Gauss para el magnetismo
Electrodinámica Ley de la fuerza de Lorentz Inducción electromagnética La ley de Faraday La ley de Lenz Corriente de desplazamiento Las ecuaciones de Maxwell Campo electromagnético Radiación electromagnética Maxwell tensor Vector de Poynting Potencial Liénard-Wiechert Ecuaciones de Jefimenko Corrientes de Foucault
Red eléctrica Corriente eléctrica Potencial eléctrico Voltaje Resistencia La ley de Ohm Circuito en serie Circuito paralelo Corriente continua Corriente alterna Fuerza electromotriz Capacidad Inductancia Impedancia Cavidades resonantes Las guías de onda
Formulación covariante Tensor electromagnético ( tensor de tensión-energía) Cuadricorriente Electromagnética de cuatro potencial
Los científicos Ampère Culombio Faraday Gauss Heaviside Henry Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

En la física , "ley, también conocido como de Gauss Gauss teorema de flujo, es una ley que relaciona la distribución de la carga eléctrica a la resultante del campo eléctrico . La ley de Gauss establece que:

La flujo eléctrico a través de cualquier superficie cerrada es proporcional a la cerrada carga eléctrica .

La ley fue formulada por Carl Friedrich Gauss en 1835, pero no fue publicado hasta 1867. Es uno de cuatro de las ecuaciones de Maxwell , que forman la base de electrodinámica clásica, siendo los otros tres La ley de Gauss para el magnetismo, Ley de Faraday, y La ley de Ampère con corrección de Maxwell. La ley de Gauss se puede utilizar para derivar la ley de Coulomb , y viceversa.

La ley de Gauss se puede expresar en su forma integral:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ frac {Q} {\ varepsilon_0},$

donde el lado izquierdo de la ecuación es una integral de superficie que denota el flujo eléctrico a través de una superficie cerrada S, y el lado derecho de la ecuación es la carga total encerrada por S dividido por el constante eléctrica.

La ley de Gauss también tiene una forma diferencial:

$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$

donde ∇ · E es el divergencia del campo eléctrico , y ρ es la cargar densidad.

Las formas integrales y diferenciales están relacionadas por la teorema de la divergencia, también llamado teorema de Gauss. Cada una de estas formas también se puede expresar de dos maneras: en términos de una relación entre el campo eléctrico E y la carga eléctrica total, o en términos de la campo de desplazamiento eléctrico D y la carga eléctrica libre.

La ley de Gauss tiene una similitud matemática cercano con una serie de leyes en otras áreas de la física, como La ley de Gauss para el magnetismo y la La ley de Gauss para la gravedad. De hecho, cualquier " la ley del cuadrado inverso "se puede formular de una manera similar a la ley de Gauss: Por ejemplo, la ley de Gauss en sí es esencialmente equivalente a la inversa del cuadrado ley de Coulomb , y la ley de Gauss para la gravedad es esencialmente equivalente a la inversa del cuadrado La ley de Newton de la gravedad.

La ley de Gauss se puede utilizar para demostrar que todos los campos eléctricos dentro de una Jaula de Faraday tiene una carga eléctrica. La ley de Gauss es algo de un análogo eléctrico de La ley de Ampère, que se ocupa de magnetismo.

En cuanto a la carga total

Forma integral

Para un volumen V con superficie S, la ley de Gauss establece que

$\ Phi_ {E, S} = \ frac {Q} {\ varepsilon_0}$

donde Φ _{E, S} es la flujo eléctrico a través de S, Q es la carga total en el interior V, y ε ₀ es la constante eléctrica. El flujo eléctrico está dada por una superficie integral sobre S:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A}$

donde E es el campo eléctrico, d A es un vector que representa una elemento infinitesimal de área , y • representa el producto escalar ..

La aplicación de la forma integral

Si el campo eléctrico es conocido en todas partes, la ley de Gauss hace que sea muy fácil, en principio, para encontrar la distribución de la carga eléctrica: La carga en una misma región se puede deducir integrando el campo eléctrico para encontrar el flujo.

Sin embargo, mucho más a menudo, es el problema inverso que necesita ser resuelto: se conoce la distribución de carga eléctrica, y el campo eléctrico tiene que ser calculado. Esto es mucho más difícil, ya que si se conoce el flujo total a través de una superficie dada, que da casi ninguna información sobre el campo eléctrico, que (por todo lo que sabes) podría entrar y salir de la superficie en patrones arbitrariamente complicados.

Una excepción es si hay alguna simetría en la situación, que obliga a que el campo eléctrico pasa a través de la superficie de una manera uniforme. Entonces, si se conoce el flujo total, el campo mismo se puede deducir en cada punto. Ejemplos comunes de simetrías que se prestan a la ley de Gauss incluyen simetría cilíndrica, simetría plana, y la simetría esférica. Vea el artículo Superficie gaussiana para ejemplos en los que estas simetrías son explotados para calcular los campos eléctricos.

Forma diferencial

En forma diferencial , la ley de Gauss establece:

$\ Mathbf {\ nabla} \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$

donde ∇ · denota divergencia, E es el campo eléctrico, y ρ es la eléctrica total cargar densidad (incluyendo cargo tanto libres y combinados), y ε ₀ es la constante eléctrica. Este es matemáticamente equivalente a la forma integral, a causa de la teorema de la divergencia.

Equivalencia de las formas integrales y diferenciales

Las formas integrales y diferenciales son matemáticamente equivalentes, por la teorema de la divergencia. Aquí es el argumento más específicamente:

La forma integral de la ley de Gauss es:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ frac {Q} {\ varepsilon_0}$

para cualquier superficie S cerrado que contiene carga Q. Por el teorema de divergencia, esta ecuación es equivalente a:

$\ Iiint \ limits_V \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V = \ frac {Q} {\ varepsilon_0}$

para cualquier volumen V que contiene carga Q. Por la relación entre la carga y la densidad de carga, esta ecuación es equivalente a:

$\ Iiint \ limits_V \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V = \ iiint \ limits_V \ frac {\ rho} {\ varepsilon_0} \ \ mathrm {d} V$

para cualquier volumen V. Para que esta ecuación para ser simultáneamente cierto para cada volumen posible V, es necesario (y suficiente) para los integrandos sean iguales en todas partes. Por lo tanto, esta ecuación es equivalente a:

$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}.$

Así, las formas integrales y diferenciales son equivalentes.

En cuanto a la carga libre

Libre contra carga estática

La carga eléctrica que se produce en las situaciones de libros de texto simples sería clasificado como "carga libre" -por ejemplo, la carga que se transfiere en la electricidad estática o la carga en un placa del condensador. Por el contrario, "carga con destino" sólo se plantea en el contexto de materiales dieléctricos (polarizables). (Todos los materiales son polarizable en cierta medida). Cuando estos materiales se colocan en un campo eléctrico externo, los electrones permanecen unidos a sus respectivos átomos, pero se desplazan una distancia microscópica en respuesta al campo, por lo que son más en un lado del átomo que el otro. Todos estos desplazamientos microscópicos se suman para dar una distribución de carga neta macroscópico, y esto constituye la "carga estática".

Aunque microscópicamente, toda la carga es fundamentalmente el mismo, a menudo hay razones prácticas para querer tratar la carga estática diferente de carga libre. El resultado es que cuanto más derecho "fundamental" de Gauss, en términos de E, a veces se pone en forma equivalente a continuación, que es en términos de D y sólo la carga libre.

Forma integral

Esta formulación de la ley de Gauss establece que, para cualquier volumen V en el espacio, con la superficie S, la siguiente ecuación:

$\ Phi_ {D, S} = Q _ {\ mathrm {libre}}, \!$

donde Φ _{D, S} es el flujo de la desplazamiento eléctrico D Campo a través de S, y Q es la carga _libre libre contenido en V. El flujo Φ _{D, S} se define de forma análoga al flujo Φ _{E, S} del campo eléctrico E a través de S. Específicamente, está dada por la integral de superficie

$\ Phi_ {D, S} = \ oint_S \ mathbf {D} \ cdot \ mathrm {d} \ mathbf {A}.$

Forma diferencial

La forma diferencial de la ley de Gauss, que implica la carga libre solamente, afirma:

$\ Mathbf {\ nabla} \ cdot \ mathbf {D} = \ rho _ {\ mathrm {libre}}$

donde ∇ · D es el divergencia del campo de desplazamiento eléctrico, y _libre ρ es la densidad de carga eléctrica libre.

La forma diferencial y forma integral son matemáticamente equivalentes. La prueba implica principalmente la teorema de la divergencia.

Equivalencia de las declaraciones totales y libres de carga

La prueba de que las formulaciones de la ley de Gauss en términos de carga libre son equivalentes a las fórmulas en las que la carga total.

En esta prueba, vamos a demostrar que la ecuación

$\ Nabla \ cdot \ mathbf {E} = \ rho / \ epsilon_0$

es equivalente a la ecuación

$\ Nabla \ cdot \ mathbf {D} = \ rho _ {\ mathrm {libre}}$

Tenga en cuenta que sólo estamos tratando con las formas diferenciales, no las formas integrales, pero eso es suficiente, ya que el diferencial y formas integrales son equivalentes en cada caso, por el teorema de la divergencia.

Introducimos el densidad de polarización P, que tiene la siguiente relación con E y D:

$\ Mathbf {D} = \ epsilon_0 \ mathbf {E} + \ mathbf {P}$

y la siguiente relación a la carga estática:

$\ Rho _ {\ mathrm {obligado}} = - \ nabla \ cdot \ mathbf {P}$

Ahora, tenga en cuenta las tres ecuaciones:

$\ Rho _ {\ mathrm {obligado}} = \ nabla \ cdot (- \ mathbf {P})$

$\ Rho _ {\ mathrm {libre}} = \ nabla \ cdot \ mathbf {D}$

$\ Rho = \ nabla \ cdot (\ epsilon_0 \ mathbf {E})$

La idea clave es que la suma de las dos primeras ecuaciones es la tercera ecuación. Esto completa la prueba: La primera ecuación es verdadera por definición, y por lo tanto la segunda ecuación es verdadera si y sólo si la tercera ecuación es verdadera. Así que la segunda y tercera ecuaciones son equivalentes, que es lo que queríamos demostrar.

En los materiales lineales

En homogéneo, isotrópico, no dispersivo, materiales lineales, hay un bonito, simple relación entre E y D:

$\ Varepsilon \ mathbf {E} = \ mathbf {D}$

donde ε es la permitividad del material. En estas circunstancias, hay otro par de formulaciones equivalentes de la ley de Gauss:

$\ Phi_ {E, S} = \ frac {Q _ {\ mathrm {libre}}} {\ varepsilon}$

$\ Mathbf {\ nabla} \ cdot \ mathbf {E} = \ frac {\ rho _ {\ mathrm {libre}}} {\ varepsilon}$

Relación con la ley de Coulomb

Derivación de la ley de Gauss de la ley de Coulomb

La ley de Gauss se puede derivar de la ley de Coulomb , que establece que el campo eléctrico debido a una estacionaria carga puntual es:

$\ Mathbf {E} (\ mathbf {r}) = \ frac {q} {4 \ pi \ epsilon_0} \ frac {\ mathbf {e_r}} {r ^ 2}$

donde

e _r es la radial vector unitario,

r es el radio, | r |,

$\ Epsilon_0$ es el constante eléctrica,

q es la carga de la partícula, que se supone que se encuentra en el origen.

Usando la expresión de la ley de Coulomb, obtenemos el campo total en r mediante el uso de una integral para sumar el campo en R debido a la carga infinitesimal en cada otro punto s en el espacio, para dar

$\ Mathbf {E} (\ mathbf {r}) = \ frac {1} {4 \ pi \ epsilon_0} \ int \ frac {\ rho (\ mathbf {s}) (\ mathbf {r} - \ mathbf {s })} {| \ mathbf {r} - \ mathbf {s} | ^ 3} d ^ 3 \ mathbf {s}$

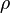donde $\ Rho$ es la densidad de carga. Si tomamos la divergencia de ambos lados de esta ecuación con respecto a r, y usamos el teorema conocido

$\ Nabla \ cdot \ left (\ frac {\ mathbf {s}} {| \ mathbf {s} | ^ 3} \ right) = 4 \ pi \ delta (\ mathbf {s})$

donde δ (s) es la Función delta de Dirac, el resultado es

$\ Nabla \ cdot \ mathbf {E} (\ mathbf {r}) = \ frac {1} {\ epsilon_0} \ int \ rho (\ mathbf {s}) \ \ delta (\ mathbf {r} - \ mathbf { s}) \ d ^ 3 \ mathbf {s}$

Utilizando el " tamizar propiedad "de la función delta de Dirac, llegamos a

$\ Nabla \ cdot \ mathbf {E} (\ mathbf {r}) = \ rho (\ mathbf {r}) / \ epsilon_0$

que es la forma diferencial de la ley de Gauss, si lo deseas.

Tenga en cuenta que, dado que la ley de Coulomb sólo se aplica a los cargos fijos, no hay razón para esperar que la ley de Gauss para mantener para los cargos basados en esta derivación solo movimiento. De hecho, la ley de Gauss se sostiene por cargas en movimiento, y en este sentido la ley de Gauss es más general que la ley de Coulomb.

Derivación de la ley de Coulomb de la ley de Gauss

En rigor, la ley de Coulomb no se puede derivar de la ley de Gauss solo, ya que la ley de Gauss no da ninguna información sobre la curvatura de E (ver Descomposición Helmholtz y La ley de Faraday). Sin embargo, la ley de Coulomb se puede demostrar a partir de la ley de Gauss si se supone, además, que el campo eléctrico de una carga puntual es esféricamente simétrico (este supuesto, al igual que la ley de Coulomb en sí, es exactamente cierto si la carga está parado, y aproximadamente cierto si la carga está en movimiento).

Tomando S en forma integral de la ley de Gauss a ser una superficie esférica de radio r, centrada en la carga puntual Q, tenemos

$\ Oint_ {S} \ mathbf {E} \ cdot d \ mathbf {A} = Q / \ varepsilon_0$

Por el supuesto de simetría esférica, el integrando es una constante que se puede sacar de la integral. El resultado es

$4 \ pi r ^ 2 \ hat {\ mathbf {r}} \ cdot \ mathbf {E} (\ mathbf {r}) = Q / \ varepsilon_0$

donde $\ Hat {\ mathbf {r}}$ es un vector unitario que apunta radialmente lejos de la carga. Una vez más por simetría esférica, puntos de E en la dirección radial, y por lo que tenemos

$\ Mathbf {E} (\ mathbf {r}) = \ frac {Q} {4 \ pi \ varepsilon_0} \ frac {\ hat {\ mathbf {r}}} {r ^ 2}$

que es esencialmente equivalente a la ley de Coulomb. Así, el inversa cuadrados dependencia derecho del campo eléctrico en la ley de Coulomb se desprende de la ley de Gauss.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Gauss%27s_law&oldid=409897377 "

We provide Linux to the World

La ley de Gauss

Antecedentes

En cuanto a la carga total

Forma integral

La aplicación de la forma integral

Forma diferencial

Equivalencia de las formas integrales y diferenciales

En cuanto a la carga libre

Libre contra carga estática

Forma integral

Forma diferencial

Equivalencia de las declaraciones totales y libres de carga

En los materiales lineales

Relación con la ley de Coulomb

Derivación de la ley de Gauss de la ley de Coulomb

Derivación de la ley de Coulomb de la ley de Gauss