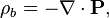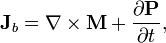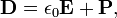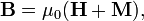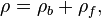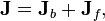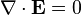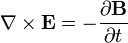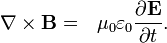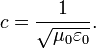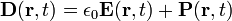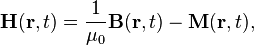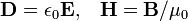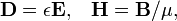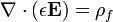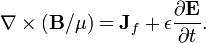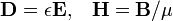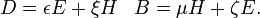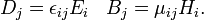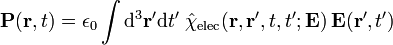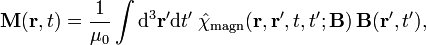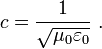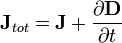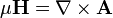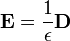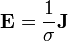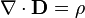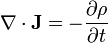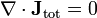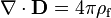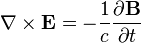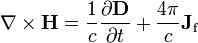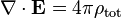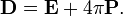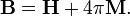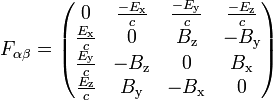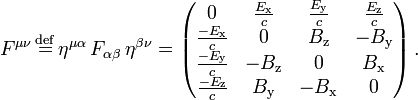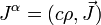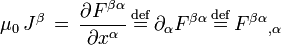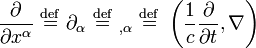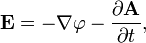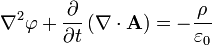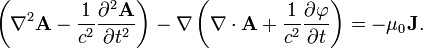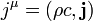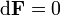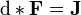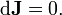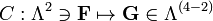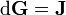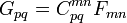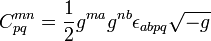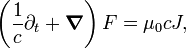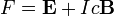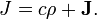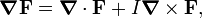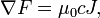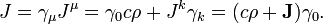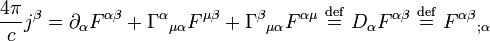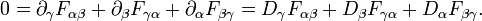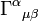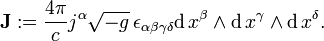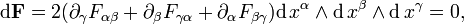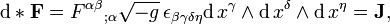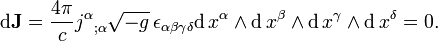Las ecuaciones de Maxwell
Antecedentes de las escuelas de Wikipedia
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/
| Electromagnetismo |
|---|
 |
Electrostática
|
Magnetoestática
|
Electrodinámica
|
Red eléctrica
|
Formulación covariante Tensor electromagnético ( tensor de tensión-energía)
|
Las ecuaciones de Maxwell son un conjunto de cuatro ecuaciones diferenciales parciales que, junto con el Ley de la fuerza de Lorentz, forman la base de electrodinámica clásica, clásicas óptica , y circuitos eléctricos. Estos a su vez son la base de la presente radio-, televisión-, teléfono-, y las tecnologías de la información.
Las ecuaciones de Maxwell tienen dos variantes principales. El conjunto "microscopio" de las ecuaciones de Maxwell utiliza carga total y la corriente total, incluyendo los cargos de nivel atómico difíciles de calcular y corrientes en los materiales. El conjunto "macroscópica" de las ecuaciones de Maxwell define dos nuevos campos auxiliares que pueden evitar una necesidad de conocer estos 'atómicas' cargas y corrientes de tamaño.
Las ecuaciones de Maxwell reciben el nombre del físico escocés y matemático James Clerk Maxwell , ya que todos se encuentran en un documento de cuatro partes, En líneas físicas de la Fuerza, que publicó entre 1861 y 1862. La forma matemática de la ley de la fuerza de Lorentz también apareció en el presente documento.
A menudo es útil para escribir las ecuaciones de Maxwell en otras formas que a menudo se llaman las ecuaciones de Maxwell también. Una formulación relativista en términos de tensores covariantes de campo se utiliza en la relatividad especial. Mientras, en la mecánica cuántica, una versión basada en el eléctrico y se prefiere potenciales magnéticos.
Descripción Conceptual
Conceptualmente, las ecuaciones de Maxwell describen cómo las cargas eléctricas y corrientes eléctricas actúan como fuentes para los campos eléctricos y magnéticos. Además, se describe cómo un campo eléctrico variable en el tiempo genera un campo magnético variable en el tiempo y viceversa. (Vea a continuación una descripción matemática de las leyes.) De las cuatro ecuaciones, dos de ellos, la ley de Gauss y La ley de Gauss para el magnetismo, describen cómo los campos emanan de cargos. (Para el campo magnético no hay una carga magnética y las líneas de los campos magnéticos, por tanto, ni comienzan ni terminan en cualquier lugar). Los otros dos ecuaciones describen cómo 'circular' los campos alrededor de sus respectivas fuentes; el campo magnético "circula" en torno a las corrientes eléctricas y variable en el tiempo del campo eléctrico en La ley de Ampère con corrección de Maxwell, mientras que "circula" el campo eléctrico alrededor de variables en el tiempo los campos magnéticos en La ley de Faraday.
La ley de Gauss
La ley de Gauss describe la relación entre un campo eléctrico y la generación de las cargas eléctricas : Los puntos de campo eléctrico lejos de cargas positivas y cargas negativas hacia. En la descripción de línea de campo, líneas de campo eléctrico comienzan sólo a cargas eléctricas positivas y terminan sólo en cargas eléctricas negativas. 'Contar' el número de líneas de campo en un superficie cerrada, por lo tanto, se obtiene la carga total encerrada por dicha superficie. Más técnicamente, se refiere al flujo eléctrico a través de cualquier hipotética cerrado " Superficie gaussiana "a la carga eléctrica dentro de la superficie.
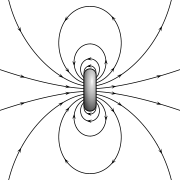
La ley de Gauss para el magnetismo
La ley de Gauss para el magnetismo afirma que no hay "cargas magnéticas" (también llamados monopolos magnéticos), análogos a cargas eléctricas. En lugar de ello, el campo magnético debido a los materiales es generado por una configuración de llamada dipolo. Dipolos magnéticos están mejor representados como bucles de corriente, pero se parecen a 'cargas magnéticas "positivos y negativos, inseparablemente unidas entre sí, que no tienen" carga magnética' red. En cuanto a las líneas de campo, esta ecuación establece que las líneas de campo magnético ni comienzan ni fin, pero hacen bucles o se extienden hasta el infinito y la espalda. En otras palabras, cualquier línea de campo magnético que entra en un volumen dado debe salir de alguna parte de ese volumen. Declaraciones técnicos equivalentes son que el total flujo magnético a través de cualquier superficie gaussiana es cero, o que el campo magnético es una campo vectorial solenoidal.
La ley de Faraday

La ley de Faraday se describe cómo variar una vez campo magnético crea ("induce") de un campo eléctrico . Este aspecto de inducción electromagnética es el principio de funcionamiento detrás de muchos generadores eléctricos: por ejemplo, una rotación de imán de barra crea un campo magnético cambiante, que a su vez genera un campo eléctrico en un alambre de cerca. (Nota: hay dos ecuaciones estrechamente relacionados que se llaman ley de Faraday La forma utilizada en las ecuaciones de Maxwell es siempre válida, pero más restrictiva que originalmente formulada por. Michael Faraday .)
La ley de Ampère con corrección de Maxwell

La ley de Ampere con la corrección de Maxwell afirma que los campos magnéticos pueden ser generados en dos formas: corriente eléctrica (esto fue la "ley de Ampère" original) y cambiando los campos eléctricos (esto fue "corrección de Maxwell").
Corrección de Maxwell a la ley de Ampere es particularmente importante: Esto significa que un campo magnético cambiante crea un campo eléctrico y un campo eléctrico variable crea un campo magnético. Por lo tanto, estas ecuaciones permiten "autosostenibles ondas electromagnéticas "para viajar a través del espacio vacío (ver ecuación de onda electromagnética).
La velocidad calculada para las ondas electromagnéticas, lo que podría predecirse a partir de experimentos con cargas y corrientes, coincide exactamente con la velocidad de la luz ; De hecho, la luz es una forma de radiación electromagnética (como lo son Los rayos X, ondas de radio, y otros). Maxwell entiende la conexión entre las ondas electromagnéticas y la luz en 1861, unificando así los campos previamente separadas del electromagnetismo y la óptica .
Unidades y resumen de las ecuaciones
Las ecuaciones de Maxwell varían con el sistema de unidades utilizado. Aunque la forma general sigue siendo la misma, diversas definiciones se cambian y diferentes constantes aparecen en diferentes lugares. Las ecuaciones de esta sección se dan en Unidades del SI. Otras unidades de uso común son Unidades de Gauss (basados en el sistema CGS), Unidades de Lorentz-Heaviside (utilizados principalmente en la física de partículas) y Unidades de Planck (utilizados en física teórica). Vea a continuación Unidades CGS-Gauss.
Para una descripción de la diferencia entre las variantes microscópicas y macroscópicas de las ecuaciones de Maxwell ver la sección correspondiente.
En las ecuaciones que figuran a continuación, los símbolos en negrita representan vector cantidades, y los símbolos en cursiva representan cantidades escalares. Las definiciones de los términos utilizados en las dos tablas de ecuaciones se dan en otra mesa inmediatamente después.
Tabla de ecuaciones '' microscópicas
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| La ley de Gauss | 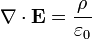 |  |
| La ley de Gauss para el magnetismo | 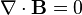 | 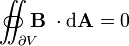 |
| Ecuación de Maxwell-Faraday (Ley de Faraday) | 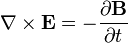 | 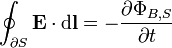 |
| Ley de Ampère (Con corrección de Maxwell) | 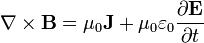 | 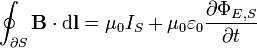 |
Tabla de ecuaciones macroscópicas ''
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| La ley de Gauss | 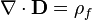 | 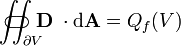 |
| La ley de Gauss para el magnetismo | 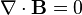 | 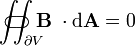 |
| Ecuación de Maxwell-Faraday ( Ley de Faraday) | 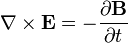 | 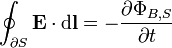 |
| Ley de Ampère (Con corrección de Maxwell) | 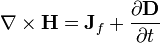 | 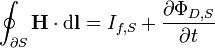 |
Tabla de términos utilizados en las ecuaciones de Maxwell
La siguiente tabla proporciona el significado de cada símbolo y el Unidad SI de medida:
| Símbolo | Significado (primer término es el más común) | Unidad SI de medición |
|---|---|---|
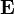 | campo eléctrico también llamada la intensidad del campo eléctrico | voltios por metros o, equivalentemente, por newton culombio |
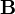 | campo magnético también llamada la inducción magnética también llamada la densidad de campo magnético también llamada la densidad de flujo magnético | tesla, o equivalentemente, weber por metro cuadrado, voltios - por segundo metro cuadrado |
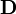 | campo de desplazamiento eléctrico también llamada la inducción eléctrica también llamada la densidad de flujo eléctrico | culombios por metro cuadrado o equivalente, newton por voltios - metro |
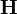 | campo de magnetización también llamado campo magnético auxiliar también llamada intensidad del campo magnético también llamado campo magnético | amperio por metro |
 | la divergencia operador | por metro (factor contribuyó mediante la aplicación de cualquiera de operador) |
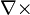 | el rizo operador | |
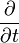 | derivada parcial con respecto al tiempo | por segundo (factor contribuyó aplicando el operador) |
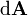 | elemento de vector diferencial de área de superficie A, con magnitud infinitamente pequeño y dirección normal a la superficie S | metros cuadrados |
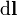 | elemento de vector diferencial de la longitud de la trayectoria tangencial a la trayectoria / curva de | metros |
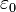 | permitividad del espacio libre, también llamado constante eléctrica, una constante universal | faradios por metro |
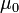 | permeabilidad del espacio libre, también llamado magnético constante, una constante universal | henrios por metro, o newtons por amperios al cuadrado |
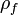 | libre densidad de carga (no incluidos carga estática) | culombios por metro cúbico |
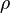 | total densidad de carga (incluyendo tanto libre y carga estática) | culombios por metro cúbico |
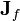 | libre densidad de corriente (no incluidos consolidado actual) | amperios por metro cuadrado |
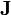 | total densidad de corriente (incluyendo tanto libre y consolidado actual) | amperios por metro cuadrado |
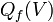 | neto libre de carga eléctrica dentro del volumen tridimensional V (no incluida carga estática) | culombios |
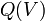 | neto carga eléctrica dentro del volumen tridimensional V (incluyendo tanto libre y carga estática) | culombios |
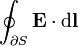 | integral de línea del campo eléctrico a lo largo del ∂S contorno de una superficie S (∂S es siempre una curva cerrada ). | joules por coulomb |
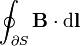 | integral de línea del campo magnético sobre las ∂S contorno cerrado de la superficie S | tesla-metros |
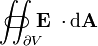 | la flujo eléctrico ( integral de superficie del campo eléctrico) a través de la ( superficie cerrada) 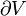 (El límite del volumen V) (El límite del volumen V) | Joule-metro por coulomb |
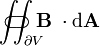 | la flujo magnético ( integral de superficie de la B-campo magnético) a través de la ( superficie cerrada) 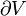 (El límite del volumen V) (El límite del volumen V) | tesla metros-cuadrado o webers |
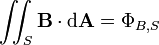 | flujo magnético a través de cualquier superficie S, no necesariamente cerrado | webers o equivalentemente, voltios-segundos |
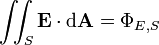 | flujo eléctrico a través de cualquier superficie S, no necesariamente cerrada | Joule metros por coulomb |
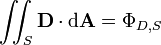 | flujo de campo de desplazamiento eléctrica a través de cualquier superficie S, no necesariamente cerrada | culombios |
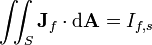 | neto libre corriente eléctrica que pasa a través de la superficie S (no incluye consolidado actual) | amperios |
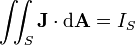 | neto corriente eléctrica que pasa a través de la superficie S (incluyendo tanto libre y consolidado actual) | amperios |
La prueba de que las dos formulaciones generales son equivalentes
Las dos formulaciones generales suplentes de las ecuaciones de Maxwell dadas anteriormente son matemáticamente equivalentes y relacionados por las siguientes relaciones:
donde P y M son polarización y magnetización, y ρ b y J b están obligados cargo y actual, respectivamente. Sustituyendo estas ecuaciones en las ecuaciones de Maxwell 'macroscópicas' da forma idéntica las ecuaciones microscópicas.
Ecuaciones "microscópicos" de Maxwell
La variante microscópica de la ecuación de Maxwell expresa el campo eléctrico E y el campo magnético B en términos de la carga total y el presente corriente total incluyendo las cargas y corrientes a nivel atómico. A veces se llama la forma general de las ecuaciones de Maxwell o "ecuaciones de Maxwell en el vacío". Ambas variantes de las ecuaciones de Maxwell son igualmente general, sin embargo, ya que son matemáticamente equivalentes. Las ecuaciones microscópicas son más útiles en guías de ondas, por ejemplo, cuando no hay materiales dieléctricos o magnéticos cerca.
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| La ley de Gauss | 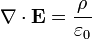 | 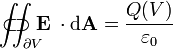 |
| La ley de Gauss para el magnetismo | 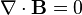 | 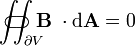 |
| Ecuación de Maxwell-Faraday (Ley de Faraday) | 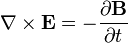 | 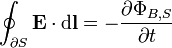 |
| Ley de Ampère (Con corrección de Maxwell) | 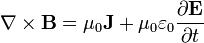 | 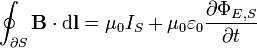 |
Con ni cargos ni corrientes
En una región sin cargos (ρ = 0) y no corrientes (J = 0), como en el vacío, las ecuaciones de Maxwell se reducen a:
Estas ecuaciones conducen directamente a E y B que satisface la ecuación de onda para que las soluciones son combinaciones lineales de ondas planas que viajan a la velocidad de la luz ,
Además, E y B son mutuamente perpendiculares entre sí y la dirección del movimiento y están en fase entre sí. La onda plana sinusoidal es una solución especial de estas ecuaciones.
De hecho, las ecuaciones de Maxwell explicar cómo estas ondas pueden propagarse físicamente por el espacio. El campo magnético cambiante crea un campo eléctrico variable a través La ley de Faraday. A su vez, ese campo eléctrico genera un campo magnético variable a través de Corrección de Maxwell a la ley de Ampère. Este ciclo perpetuo permite que estas ondas, ahora conocido como radiación electromagnética , que se mueven por el espacio a la velocidad c.
Ecuaciones macroscópicas '' de Maxwell
A diferencia de las ecuaciones microscópicas '', "las ecuaciones macroscópicas de Maxwell", también conocidas como las ecuaciones de Maxwell en la materia, el factor de la carga estática y la corriente para obtener las ecuaciones que dependen sólo de las cargas y corrientes libres. Estas ecuaciones son más similares a las que el propio Maxwell introdujo. El costo de esta factorización es que los campos adicionales necesitan ser definidos: el campo de desplazamiento D que se define en términos del campo eléctrico E y el la polarización P del material, y el campo de tarjeta magnética H, que se define en términos del campo y el Magnéticos B magnetización M del material.
Carga estática y corriente
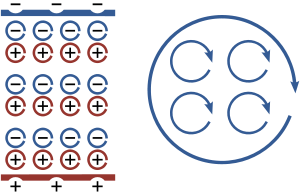
Cuando un campo eléctrico se aplica a una de material dieléctrico sus moléculas responden mediante la formación de microscópica dipolos eléctricos-sus núcleos atómicos se mueven una pequeña distancia en la dirección del campo, mientras que sus electrones se mueven una pequeña distancia en la dirección opuesta. Esto produce una carga estática macroscópico en el material a pesar de todos los cargos involucrados están obligados a moléculas individuales. Por ejemplo, si cada molécula responde de la misma, similar a la mostrada en la figura, estos pequeños movimientos de la carga se combinan para producir una capa de positivo unido carga en un lado del material y una capa de carga negativa en el otro lado. La carga estática se describe más convenientemente en términos de una la polarización, P, en el material. Si P es uniforme, una separación macroscópica de carga se produce sólo en las superficies donde P entrar y salir del material. Para P no uniforme, una carga también se produce en la mayor parte.
Algo similar, en todos los materiales de la exposición átomos constituyentes momentos magnéticos que están intrínsecamente vinculados a la el momento angular de los componentes de los átomos, más notablemente sus electrones. La conexión con momento angular sugiere la imagen de un conjunto de bucles de corriente microscópicas. Fuera de la tela, un conjunto de tales bucles de corriente microscópicas no es diferente de una corriente macroscópica que circula alrededor de la superficie del material, a pesar del hecho de que ningún momento magnético individuo se desplaza una distancia grande. Estos corrientes consolidados pueden describirse mediante el magnetización M.
El muy complicado y granulares obligado cargas y corrientes consolidados, por lo tanto, pueden ser representados en la escala macroscópica en términos de P y M que promedian estas cargas y corrientes en una escala suficientemente grande para que no se vea la granularidad de los átomos individuales, pero también lo suficientemente pequeñas que varían con la ubicación en el material. Como tal, las ecuaciones macroscópicas de Maxwell ignora muchos detalles sobre una escala fina que puede ser poco importante para la comprensión de los asuntos en una escala más grosera mediante el cálculo de los campos que se promedian en un poco de volumen de tamaño adecuado.
Ecuaciones
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| La ley de Gauss | 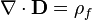 | 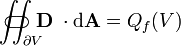 |
| La ley de Gauss para el magnetismo | 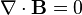 | 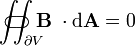 |
| Ecuación de Maxwell-Faraday ( Ley de Faraday) | 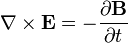 | 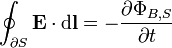 |
| Ley de Ampère (Con corrección de Maxwell) | 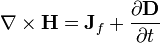 | 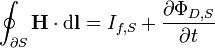 |
Relaciones constitutivas
Para la aplicación de 'ecuaciones macroscópicas de Maxwell', es necesario especificar las relaciones entre campo de desplazamiento D y E, y el H-campo magnético H y B. Estas ecuaciones especifican la respuesta de carga estática y corriente a los campos aplicados y se llaman relaciones constitutivas.
La determinación de la relación constitutiva entre los campos auxiliares D y H y los campos E y B comienza con la definición de los propios campos auxiliares:
donde P es la campo de polarización y M es el campo de magnetización que se define en términos de cargas microscópicas atado y obligado actual respectivamente. Antes de llegar a la forma de calcular M y P es útil examinar algunos casos especiales, sin embargo.
Sin materiales magnéticos o dieléctricos
En la ausencia de materiales magnéticos o dieléctricos, las relaciones constitutivas son simples:
donde ε 0 y μ 0 son dos constantes universales, llamado permitividad de espacio libre y permeabilidad del espacio libre, respectivamente. Sustituyendo estos de nuevo en las ecuaciones de Maxwell macroscópicas conducen directamente a las ecuaciones de Maxwell microscópicas, excepto que las corrientes y cargas se sustituyen con corrientes libres y cargas libres. Se espera que esto ya no hay cargos encuadernados ni corrientes.
Materiales isótropos lineales
En una ( isotrópico) material lineal, donde P es proporcional a E y M es proporcional a B las relaciones constitutivas también son sencillos. En términos de la polarizaton P y la magnetización M son:
donde χ χ m e y son el eléctrico y susceptibilidades magnéticas de un material dado, respectivamente. En términos de D y H las relaciones constitutivas son:
donde ε y μ son constantes (que dependen del material), llamado permitividad y permeabilidad, respectivamente, del material. Estos están relacionados con las susceptibilidades por:
Sustituyendo en las relaciones constitutivas anteriormente en las ecuaciones de Maxwell en lineales, dispersionless, materiales invariantes en el tiempo (sólo de forma diferencial) son:
Estos son formalmente idéntica a la formulación general en términos de E y B (dado anteriormente), excepto que el permitividad de espacio libre fue sustituido por el permitividad del material, la permeabilidad del espacio libre fue sustituido por el permeabilidad del material, y sólo cargas y corrientes gratuitas se incluyen (en lugar de todas las cargas y corrientes). A menos que el material es homogéneo en el espacio, ε y μ no se puede factorizar de las expresiones derivadas de los laterales izquierdos.
Caso general
Para materiales del mundo real, las relaciones constitutivas no son lineales, excepto aproximadamente. Cálculo de las relaciones constitutivas de los primeros principios consiste en determinar cómo se crean P y M de una E y B dado. Estas relaciones pueden ser empíricos (basados directamente en las mediciones), o teórico (basado en la mecánica estadística , teoría de transporte u otras herramientas de la física de la materia condensada ). El detalle empleada puede macroscópica o microscópico, dependiendo del nivel necesario para el problema bajo escrutinio.
En general, aunque las relaciones constitutivas pueden por lo general todavía escribirse:
pero ε y μ no son, en general, las constantes simples, sino más bien funciones. Ejemplos son:
- Dispersión y absorción donde ε y μ son funciones de la frecuencia. (Causalidad no permiten que los materiales que no dispersivo; véase, por ejemplo, Kramers-Kronig relaciones). Tampoco los campos deben estar en fase que conduce a ser ε y μ complejo . Esto también conduce a la absorción.
- Bi (a) isotropía donde H y D dependen tanto de B y E:
- No linealidad donde ε y μ son funciones de E y B.
- Anisotropía (tales como o birrefringencia dicroísmo) que se produce cuando ε y μ son de segunda fila tensores,
- La dependencia de P y M en E y B en otros lugares y tiempos. Esto podría ser debido a la falta de homogeneidad espacial; por ejemplo en una estructura domained, o una heteroestructura de cristal líquido , o más comúnmente en la situación en la que simplemente hay múltiples materiales que ocupan diferentes regiones del espacio). O podría ser debido a una variación de medio tiempo o debido a histéresis. En tales casos P y M se puede calcular como:
- en el que las funciones de permitividad y permeabilidad son reemplazados por integrales sobre el más general eléctrico y susceptibilidades magnéticas.
En la práctica, algunas propiedades de los materiales tienen un impacto insignificante en circunstancias particulares, lo que permite el abandono de pequeños efectos. Por ejemplo: no linealidades ópticas se pueden despreciar para bajas intensidades de campo; dispersión de los materiales no es importante cuando la frecuencia se limita a un estrecho ancho de banda; material de absorción se puede despreciar para longitudes de onda para la que un material es transparente; y metales con conductividad finita menudo se aproximan a microondas o longitudes de onda más largas como metales perfectos con conductividad infinita (formando barreras duras con cero profundidad de la piel de la penetración de campo).
Cabe señalar que los materiales hechos por el hombre pueden ser diseñados para tener permitividad y la permeabilidad a medida, tales como metamateriales y cristales fotónicos.
Cálculo de las relaciones constitutivas
En general, las ecuaciones constitutivas se determinan teóricamente mediante el cálculo de cómo una molécula responde a los campos locales a través de la Fuerza de Lorentz. Pueden necesitar ser modelado, así como vibraciones de la red en los cristales o las fuerzas de bonos Otras fuerzas. Incluyendo todas las fuerzas conduce a cambios en la molécula que se utilizan para calcular P y M como una función de los campos locales.
Los campos locales difieren de los campos aplicados debido a los campos producidos por la polarización y la magnetización del material de cerca; un efecto que también tiene que ser modelado. Además, los materiales reales no son medios continuos; los campos locales de materiales reales varían enormemente en la escala atómica. Los campos deben ser promediados sobre un volumen adecuado para formar una aproximación continua.
Estas aproximaciones continuum menudo requieren algún tipo de mecánica cuántica análisis como la teoría cuántica de campos en su aplicación a la física de la materia condensada . Véase, por ejemplo, teoría funcional de la densidad, Relaciones Kubo verdes y Función de Green. Varios ecuaciones aproximadas de transporte han evolucionado, por ejemplo, el Ecuación de Boltzmann o la Ecuación de Fokker-Planck o la Ecuaciones de Navier-Stokes. Algunos ejemplos en los que se aplican estas ecuaciones son magnetohidrodinámica, dinámica de fluidos, electrohidrodinámica, la superconductividad , modelado de plasma. Un aparato físico todo para hacer frente a estas cuestiones ha desarrollado. Un conjunto diferente de los métodos de homogeneización (en evolución de una tradición en materiales de tratamiento como conglomerados y laminados) se basan en la aproximación de un material no homogéneo por un homogénea medio efectivo (válido para excitaciones con longitudes de onda mucho mayor que la escala de la falta de homogeneidad).
El modelo teórico de las propiedades continuum aproximación de muchos materiales reales a menudo se basan en la medición, así, por ejemplo, mediciones elipsometría.
Historia
Relación entre la electricidad, el magnetismo y la velocidad de la luz
La relación entre la electricidad, el magnetismo y la velocidad de la luz se puede resumir en la ecuación moderna:
El lado izquierdo es la velocidad de la luz, y el lado derecho es una cantidad relacionada con las ecuaciones que gobiernan la electricidad y el magnetismo. Aunque el lado derecho tiene unidades de velocidad, se puede inferir a partir de mediciones de fuerzas eléctricas y magnéticas, que implican no hay velocidades físicas. Por lo tanto, el establecimiento de esta relación proporciona evidencia convincente de que la luz es un fenómeno electromagnético.
El descubrimiento de esta relación comenzó en 1855, cuando Wilhelm Eduard Weber y Rudolf Kohlrausch determinó que había una cantidad relacionada con la electricidad y el magnetismo, "la relación de la unidad electromagnética absoluta de forma gratuita a la unidad electrostática absoluta del cargo" (en lenguaje moderno, el valor 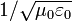 ), Y determinó que debe tener unidades de velocidad. Entonces midieron esta relación en un experimento que involucró a la carga y descarga de un Botella de Leyden y la medición de la fuerza magnética de la corriente de descarga, y se encontró un valor de 3.107 × 10 8 m / s, muy cerca de la velocidad de la luz, que recientemente había sido medidos a 3,14 × 10 8 m / s por Hippolyte Fizeau en 1848 y al 2,98 × 10 8 m / s por Léon Foucault en 1850. Sin embargo, Weber y Kohlrausch no hizo la conexión a la velocidad de la luz. Hacia el final de 1861 mientras trabajaba en la parte III de su papel En líneas físicas de fuerza, Maxwell viajó desde Escocia a Londres y miró hacia arriba Weber y los resultados de Kohlrausch. Él los convierte en un formato que es compatible con sus propios escritos, y al hacerlo, él estableció la conexión a la velocidad de la luz y llegó a la conclusión de que la luz es una forma de radiación electromagnética.
), Y determinó que debe tener unidades de velocidad. Entonces midieron esta relación en un experimento que involucró a la carga y descarga de un Botella de Leyden y la medición de la fuerza magnética de la corriente de descarga, y se encontró un valor de 3.107 × 10 8 m / s, muy cerca de la velocidad de la luz, que recientemente había sido medidos a 3,14 × 10 8 m / s por Hippolyte Fizeau en 1848 y al 2,98 × 10 8 m / s por Léon Foucault en 1850. Sin embargo, Weber y Kohlrausch no hizo la conexión a la velocidad de la luz. Hacia el final de 1861 mientras trabajaba en la parte III de su papel En líneas físicas de fuerza, Maxwell viajó desde Escocia a Londres y miró hacia arriba Weber y los resultados de Kohlrausch. Él los convierte en un formato que es compatible con sus propios escritos, y al hacerlo, él estableció la conexión a la velocidad de la luz y llegó a la conclusión de que la luz es una forma de radiación electromagnética.
Ecuaciones El término de Maxwell
Las cuatro ecuaciones de Maxwell modernas se pueden encontrar de forma individual a través de su papel de 1861, derivado teóricamente utilizando un modelo de vórtice molecular de Michael Faraday "líneas de fuerza" y en conjunto con el resultado experimental de Weber y Kohlrausch 's. Pero no fue hasta 1884 que Oliver Heaviside, al mismo tiempo que un trabajo similar por Willard Gibbs y Heinrich Hertz, agrupa los cuatro juntos en un conjunto distinto. Este grupo de cuatro ecuaciones era conocido indistintamente como las ecuaciones de Hertz-Heaviside y las ecuaciones de Maxwell-Hertz, y son a veces todavía se conoce como las ecuaciones de Maxwell-Heaviside.
La contribución de Maxwell a la ciencia en la producción de estas ecuaciones se encuentra en la corrección que hizo a Ley de Ampère en su documento de 1861 En líneas físicas de la Fuerza. Agregó el desplazamiento actual mandato de Ley de Ampère y esto le permitió obtener la ecuación de onda electromagnética en su trabajo posterior 1865 Una teoría dinámica del campo electromagnético y demostrar el hecho de que la luz es una onda electromagnética . Este hecho fue posteriormente confirmada experimentalmente por Heinrich Hertz en 1887. El físico Richard Feynman predijo que, "La Guerra Civil estadounidense insignificantes provincial en comparación con este importante evento científico de la misma década."
. El concepto de campos se introdujo por, entre otros, Faraday Albert Einstein escribió:
La formulación precisa de las leyes del espacio-tiempo fue obra de Maxwell. Imagina sus sentimientos cuando las ecuaciones diferenciales que había formulado demostraron lo que los campos electromagnéticos repartidos en forma de ondas polarizadas, ya la velocidad de la luz! A pocos hombres en el mundo se ha concedido una experiencia así ... que tomó algunas décadas los físicos a comprender el pleno significado del descubrimiento de Maxwell, tan audaz fue el salto que su genio forzado sobre las concepciones de sus compañeros de trabajo- (Science 24 de mayo de 1940)
Heaviside trabajó para eliminar los potenciales ( potencial eléctrico y potencial magnético) que Maxwell había usado como los conceptos centrales en sus ecuaciones; este esfuerzo fue algo polémico, aunque se entendía por 1884 que los potenciales deben propagar a la velocidad de la luz como los campos, a diferencia del concepto de acción a una distancia instantánea como el entonces concepción del potencial gravitatorio. El análisis moderno de, por ejemplo, antenas de radio, hace un uso completo de vectoriales y escalares potenciales de Maxwell para separar las variables, una técnica común utilizada para formular las soluciones de las ecuaciones diferenciales. Sin embargo los potenciales pueden introducirse por manipulación algebraica de las cuatro ecuaciones fundamentales.
En líneas físicas de la Fuerza
Las cuatro ecuaciones de Maxwell modernos días aparecieron en toda el papel En líneas físicas de la Fuerza de Maxwell 1861:
- La ecuación (56) en el papel de Maxwell 1861 es ∇ ⋅ B = 0.
- La ecuación (112) es Ley de Ampère con corriente de desplazamiento de Maxwell añadió. Es la adición de corriente de desplazamiento que es el aspecto más importante de la obra de Maxwell en el electromagnetismo , ya que le permitió sacar adelante la ecuación de onda electromagnética en su artículo 1865 Una teoría dinámica del campo electromagnético, y por lo tanto muestran que la luz es una onda electromagnética. Por tanto, es este aspecto de la obra de Maxwell que da las ecuaciones de su pleno significado. (Curiosamente, Kirchhoff deriva el ecuaciones del telegrafista en 1857 sin utilizar corriente de desplazamiento. Pero él hizo uso de la ecuación de Poisson y la ecuación de continuidad, que son los ingredientes matemáticos de la corriente de desplazamiento. Sin embargo, Kirchhoff cree sus ecuaciones para ser aplicable sólo dentro de un cable eléctrico y por eso no se le atribuye haber descubierto que la luz es una onda electromagnética).
- La ecuación (115) es la ley de Gauss .
- La ecuación (54) es una ecuación que Oliver Heaviside conoce como 'la ley de Faraday'. Esta ecuación es apto para la variable en el tiempo aspecto de la inducción electromagnética, pero no para el aspecto inducida mocionalmente, mientras que la ley de flujo original del Faraday atiende a ambos aspectos. Maxwell se ocupa del aspecto mocionalmente dependiente de la inducción electromagnética, v × B , en la ecuación (77). La ecuación (77), que es la misma que la ecuación (D) en los ocho ecuaciones originales de Maxwell se enumeran a continuación, corresponde a todos los efectos a la moderna ley de la fuerza días F = q ( E + v × B ), que se encuentra junto a las ecuaciones de Maxwell y lleva el nombre de Lorentz fuerza, a pesar de que Maxwell deriva cuando Lorentz era todavía un niño.
La diferencia entre elBy losHvectores se remonta al papel de Maxwell 1855 tituladoEn las líneas de fuerza de Faradayque fue leído a la Cambridge Philosophical Society. El documento presenta un modelo simplificado de la obra de Faraday, y cómo se relacionaron los dos fenómenos.Redujo todo el conocimiento actual en un conjunto relacionado deecuaciones diferenciales.
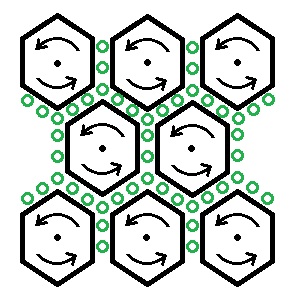
Más tarde se aclaró en su concepto de un mar de vórtices moleculares que aparece en su documento de 1861 En líneas físicas de la Fuerza. Dentro de ese contexto, H representa vorticidad puro (spin), mientras que B era una vorticidad ponderada que se pondera por la densidad del mar vórtice. Maxwell considera permeabilidad magnética μ ser una medida de la densidad de la mar vórtice. Por lo tanto la relación,
- Corriente de inducción magnéticacausa una densidad de corriente magnética
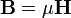
era esencialmente una analogía de rotación a la relación de corriente eléctrica lineal,
- Corriente de convección eléctrico
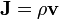
donde ρ es la densidad de carga eléctrica. B fue visto como una especie de corriente magnética de vórtices alineados en sus planos axiales, con H siendo la velocidad circunferencial de los vórtices. Con μ representa la densidad de vórtice, se deduce que el producto de μ con vorticidad H conduce a la campo magnético indicado como B .
La ecuación de la corriente eléctrica puede ser vista como una corriente de convección de carga eléctrica que implica movimiento lineal. Por analogía, la ecuación magnética es una corriente inductiva implica giro. No hay movimiento lineal en la corriente inductiva a lo largo de la dirección de la B vector. La corriente inductiva magnética representa líneas de fuerza. En particular, representa las líneas de fuerza de ley del cuadrado inverso.
La extensión de las consideraciones anteriores confirma que, cuando B es H , y donde J es ρ , entonces se sigue necesariamente de la ley de Gauss y de la ecuación de continuidad de carga que E es D . es decir, B paralelismos con E , mientras que H paralelismos con D .
Una teoría dinámica del campo electromagnético
En 1864 Maxwell publicó una teoría dinámica del campo electromagnético en el que se demostró que la luz era un fenómeno electromagnético. La confusión sobre el término "ecuaciones de Maxwell" se agrava debido a que también se utiliza a veces para un conjunto de ocho ecuaciones que aparecen en la parte III de 1864 el papel de Maxwell Una teoría dinámica del campo electromagnético, titulado "Ecuaciones generales del campo electromagnético", un confusión agravada por la escritura de seis de los ocho ecuaciones como tres ecuaciones separadas (una para cada uno de los ejes cartesianos), resultando en veinte ecuaciones y veinte incógnitas. (Como se señaló anteriormente, esta terminología no es común: referencias modernas al término "ecuaciones de Maxwell" se refieren a las revalorizaciones Heaviside.)
Los ocho ecuaciones originales de Maxwell pueden ser escritos en notación vectorial moderna de la siguiente manera:
- (A) La ley de las corrientes totales
- (B) La ecuación de la fuerza magnética
- Ley circuital (C) de Ampère
- Fuerza (D) electromotriz creada por convección, por inducción, y por la electricidad estática. (Esto es, en efecto, la fuerza de Lorentz)
- (E) La ecuación de elasticidad eléctrico
- Ley (F) de Ohm
- Ley (G) de Gauss
- (H) La ecuación de continuidad
o
- Notación
- Hes elcampo de magnetización, que Maxwell llama laintensidad magnética.
- Jes ladensidad de corriente (conJ totes la corriente total incluyendo corriente de desplazamiento).
- D es el campo de desplazamiento (llamado eldesplazamiento eléctricopor Maxwell).
- ρes ladensidad de carga libre (llamada lacantidad de electricidad gratuitapor Maxwell).
- Aes elpotencial magnético (llamado elimpulso angularpor Maxwell).
- Ese denominafuerza electromotrizpor Maxwell. El término fuerza electromotriz se utiliza hoy en día para la tensión, pero es claro por el contexto que el significado de Maxwell correspondía más al término modernocampo eléctrico.
- φes elpotencial eléctrico (que Maxwell también llamadopotencial eléctrico).
- σes laconductividad eléctrica (Maxwell llamó a la inversa de la conductividad de laresistencia específica, lo que ahora se llama laresistividad).
Es interesante observar laμ v×Htérmino que aparece en la ecuación D. Ecuación D es por lo tanto efectivamente lafuerza de Lorentz, de manera similar a la ecuación (77) de su papel 1861 (ver arriba).
Cuando Maxwell deriva la ecuación de onda electromagnética en su artículo 1865, utiliza la ecuación D para atender a la inducción electromagnética en lugar de la ley de inducción de Faraday, que se utiliza en los textos modernos. (Ley de Faraday en sí no aparece entre sus ecuaciones.) Sin embargo, Maxwell deja caer la μ v × H término de la ecuación D cuando está derivando la ecuación de onda electromagnética, ya que considera que la situación sólo desde el sistema en reposo.
Tratado sobre Electricidad y Magnetismo
En Tratado sobre Electricidad y Magnetismo, un 1,873tratado sobreel electromagnetismoescrito porJames Clerk Maxwell, once ecuaciones generales del campo electromagnético se enumeran y éstos incluyen los ocho que se enumeran en el documento 1865.
Ecuaciones de Maxwell y la relatividad
Ecuaciones originales de Maxwell se basan en la idea de que la luz viaja a través de un mar de vórtices moleculares conocidos como el " éter luminoso ', y que la velocidad de la luz tiene que ser correspondiente al marco de referencia de este éter. Medidas destinadas a medir la velocidad de la Tierra a través del éter en conflicto, sin embargo.
Un enfoque más teórico fue sugerido por Hendrik Lorentz, junto con George FitzGerald y Joseph Larmor. Tanto Larmor (1897) y Lorentz (1899, 1904) derivan de la transformación de Lorentz (llamado así por Henri Poincaré) como uno bajo el cual las ecuaciones de Maxwell eran invariables. Poincaré (1900) analizó la coordinación de movimiento relojes mediante el intercambio de señales de luz. También estableció matemáticamente la propiedad de grupos de la transformación de Lorentz (Poincaré 1905).
Einstein rechazó el éter como innecesaria y concluyó que las ecuaciones de Maxwell predicen la existencia de una velocidad fija de la luz, independiente de la velocidad del observador, y como tal utiliza las ecuaciones de Maxwell como el punto de partida de su teoría especial de la relatividad . Al hacerlo, estableció la transformación de Lorentz como documento válido para toda la materia y no sólo a las ecuaciones de Maxwell. Las ecuaciones de Maxwell jugaron un papel clave en el papel famosa de Einstein sobre la relatividad especial; por ejemplo, en el párrafo inicial del papel, que motivó su teoría señalando que una descripción de un conductor que se mueve con respecto a un imán debe generar un conjunto coherente de los campos con independencia de si la fuerza se calcula en el marco de reposo del imán o la del conductor.
General de la relatividad también ha tenido una estrecha relación con las ecuaciones de Maxwell. Por ejemplo, Theodor Kaluza y Oskar Klein mostró en la década de 1920 que las ecuaciones de Maxwell pueden derivarse mediante la ampliación de la relatividad general en cinco dimensiones. Esta estrategia de utilizar las dimensiones superiores para unificar diferentes fuerzas sigue siendo un área activa de investigación en física de partículas .
Modificado para incluir los monopolos magnéticos
Las ecuaciones de Maxwell del electromagnetismo se relacionan los campos eléctricos y magnéticos a los movimientos de cargas eléctricas. La forma estándar de las ecuaciones prevé una carga eléctrica, pero postulan sin carga magnética. No hay analógico magnético conocido de un electrón, sin embargo recientemente los científicos han descrito el comportamiento en un estado cristalino de la materia conocido como spin-hielo que tienen comportamiento macroscópico como monopolos magnéticos. (De acuerdo con el hecho de que carga magnética nunca se ha visto y puede no existir). A excepción de esto, las ecuaciones son simétricas bajo intercambio de campo eléctrico y magnético. De hecho, las ecuaciones simétricas pueden escribirse cuando todos los cargos son cero, y así es como el se deriva la ecuación de onda (ver inmediatamente anterior).
Totalmente ecuaciones simétricas también se pueden escribir si se permite la posibilidad de cargas magnéticas. Con la inclusión de una variable para estas cargas magnéticas, dicen ρ m , también habrá una variable "magnética actual" en las ecuaciones, J m . Las ecuaciones de Maxwell extendidas (en unidades cgs gaussiana) son los siguientes:
Nombre Sin monopolos magnéticos Con monopolos magnéticos (hipotética) La ley de Gauss: 

La ley de Gauss para el magnetismo: 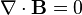

Ecuación de Maxwell-Faraday
( La ley de inducción de Faraday):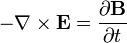
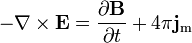
La ley de Ampère
(Con la extensión de Maxwell):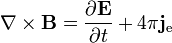
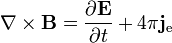
Si no existen cargas magnéticas, o si es que existen, pero donde no están presentes en una región, a continuación, las nuevas variables son cero, y las ecuaciones simétricas reducen a las ecuaciones convencionales de electromagnetismo como ∇ ·B= 0.
Las condiciones de contorno usando las ecuaciones de Maxwell
Como todos los sistemas de ecuaciones diferenciales, ecuaciones de Maxwell no se pueden resolver de forma única y sin un conjunto adecuado delas condiciones de contorno ycondiciones iniciales.
Por ejemplo, considere una región sin cargos y sin corrientes. Una solución particular que satisface todas las ecuaciones de Maxwell en esa región es que tanto E y B = 0 en todas partes en la región. Esta solución es obviamente falso si hay un cargo a las afueras de la región. En este ejemplo particular, todos los campos eléctricos y magnéticos en el interior son debido a las cargas fuera del volumen. Diferentes cargas fuera del volumen producir diferentes campos de la superficie de ese volumen y por lo tanto tienen un diferentes condiciones de contorno. En general, conocer las condiciones de contorno adecuadas para una determinada región, junto con las corrientes y cargas de la región permite que uno resuelve para todos los campos de todo el mundo dentro de esa región. Un ejemplo de este tipo es un un problema de dispersión electromagnética, donde una onda electromagnética se origina fuera de la región de dispersión es dispersada por un objetivo, y la onda electromagnética dispersa se analiza para la información que contiene sobre el objetivo en virtud de la interacción con el objetivo durante la dispersión.
En algunos casos, como guías de onda o cavidad resonadores, la región solución es en gran parte aislado del universo, por ejemplo, por las paredes metálicas, y las condiciones de contorno en las paredes definen los campos con influencia del mundo exterior se limita a los extremos de entrada / salida de la estructura. En otros casos, el universo en general a veces se aproxima por un límite de absorción artificial, o, por ejemplo para irradiar antenas o los satélites de comunicación, estas condiciones de contorno pueden tomar la forma de límites asintóticos impuestas a la solución. Además, por ejemplo en una fibra óptica o la óptica de película delgada, la región solución a menudo se divide en subregiones con sus propias propiedades simplificados, y las soluciones en cada subregión debe unirse el uno al otro a través de las interfaces subregión utilizando condiciones de contorno. Un ejemplo particular de este uso de condiciones de contorno es la sustitución de un material con una polarización volumen por una capa de superficie cargada, o de un material con una magnetización volumen por una corriente superficial, como se describe en la sección Bound carga y corriente .
Los siguientes son algunos enlaces de carácter general relativas a problemas de contorno: Ejemplos de problemas de contorno, la teoría de Sturm-Liouville, condición de contorno Dirichlet, condición de contorno Neumann, condición de frontera mixta, condición de frontera de Cauchy, Sommerfeld condición radiación. Ni que decir tiene, hay que elegir las condiciones de contorno adecuadas para el problema que se resuelve. Ver también Kempel y el libro de Friedman.
Unidades de Gauss
Unidades de Gauss es un popular variante electromagnetismo del segundo sistema gramo centímetro de unidades (cgs). En unidades gaussianas, las ecuaciones de Maxwell son:
donde c es la velocidad de la luz en el vacío. Las ecuaciones microscópicas son:
La relación entrecampo de desplazamiento eléctrico,campo eléctricoyla densidad de polarización es:
Y del mismo modo la relación entre la inducción magnética,el campo magnético y el total dela magnetización es:
En la aproximación lineal, lasusceptibilidad eléctrica ysusceptibilidad magnética se definen de manera que:
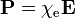 ,
, 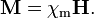
(Nota:. Aunque las susceptibilidades son números adimensionales en ambos cgs y SI, difieren en valor por un factor de 4π) La permitividad y permeabilidad son:
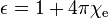 ,
, 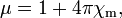
de modo que
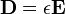 ,
, 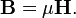
En el vacío,ε=μ= 1, por lo tanto,D=E, yB=H.
La fuerza ejercida sobre una partícula cargada por elcampo eléctricoycampo magnético viene dada por laecuación de fuerza de Lorentz:
donde q es la carga en la partícula y v es la velocidad de la partícula. Esta cifra es ligeramente diferente de la expresión SI-unidad de arriba. Por ejemplo, el campo magnético B tiene las mismas unidades que el campo eléctrico E .
Algunas ecuaciones en el artículo se dan en unidades de Gauss, pero no SI o viceversa. Afortunadamente, hay reglas generales para convertir de una a la otra; Consulte el artículo de unidades de Gauss para obtener más detalles.
Formulaciones alternativas de las ecuaciones de Maxwell
La relatividad especial motivó una formulación matemática compacta de las ecuaciones de Maxwell, en términos detensores covariantes.La mecánica cuánticatambién motivó otras formulaciones.
Por ejemplo, considere un conductor que se mueve en el campo de un imán. En el marco del imán, que experimenta un conductor magnético fuerza. Pero en el marco de un conductor que se mueve en relación con el imán, el conductor experimenta una fuerza debido a un eléctrica campo. La formulación siguiente muestra cómo las ecuaciones de Maxwell toman la misma forma en cualquier sistema de coordenadas inercial.
Formulación covariante de las ecuaciones de Maxwell
En la relatividad especial, con el fin de expresar más claramente el hecho de que las ecuaciones de Maxwell ('microscópicos') tienen la misma forma en cualquier sistema de coordenadas inercial, las ecuaciones de Maxwell están escritos en términos de cuatro-vectores y tensores en el "manifiestamente forma covariante ". Los componentes puramente espaciales de los siguientes están en Unidades del SI.
Un ingrediente en esta formulación es eltensor electromagnético, una covariante antisimétrica rango-2tensor combinación de los campos eléctricos y magnéticos:
y el resultado de elevar sus índices
El otro componente es elde cuatro actuales:
dondeρes ladensidad de carga yJes ladensidad de corriente.
Con estos ingredientes, las ecuaciones de Maxwell se pueden escribir:
y
La primera ecuación tensorial es una expresión de las dos ecuaciones no homogéneas de Maxwell, la ley de Gauss y la ley de Ampere con la corrección de Maxwell. La segunda ecuación es una expresión de las dos ecuaciones homogéneas, la ley de Faraday de la inducción y la ley de Gauss para el magnetismo. La segunda ecuación es equivalente a
donde 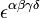 es la versión contravariante delsímbolo de Levi-Civita, y
es la versión contravariante delsímbolo de Levi-Civita, y
es el 4-degradado. En las ecuaciones tensoriales anteriores, índices repetidos se suman más de acuerdo con la convención de suma de Einstein. Hemos mostrado los resultados en varias notaciones comunes. Superior y los componentes inferiores de un vector, v α y v α , respectivamente, se intercambian con el tensor fundamental g , por ejemplo, g = η = diag (-1, 1, 1, 1).
También existen presentaciones covariantes alternativos de las ecuaciones de Maxwell, por ejemplo en términos decuatro posibilidades; ver formulación covariante del electromagnetismo clásico para más detalles.
Formulación Potencial
En la mecánica clásica de avanzada y en la mecánica cuántica (donde es necesario) a veces es útil para expresar las ecuaciones de Maxwell en una 'formulación potencial "que implica el potencial eléctrico (también llamado potencial escalar), φ , y el potencial magnético, A , (también llamado potencial vector). Estos se definen tal que:
Con estas definiciones, las dos ecuaciones homogéneas de Maxwell (Ley de Faraday y ley de Gauss para el magnetismo) se satisfacen de forma automática y las otras dos ecuaciones (homogéneas) dan las siguientes ecuaciones (para "ecuaciones de Maxwell microscópicos"):
Estas ecuaciones, en conjunto, son tan poderosos y completa como las ecuaciones de Maxwell. Por otra parte, si trabajamos sólo con las potencialidades e ignoramos los campos, el problema se ha reducido un poco, ya que los campos eléctricos y magnéticos tienen cada uno tres componentes que deben ser resueltos para (seis componentes en total), mientras que los potenciales eléctricos y magnéticos tienen sólo cuatro componentes en total.
Muchas opciones diferentes de A y φ son consistentes con un dado E y B , haciendo que estas opciones equivalente físicamente - una flexibilidad conocida como la libertad de calibre. Elección adecuada de A y φ puede simplificar estas ecuaciones, o puede adaptarlos para adaptarse a una situación particular.
Cuatro potencial
En el Calibre Lorentz, las dos ecuaciones que representan los potenciales se puede reducir a uno manifiestamenteecuación invariante Lorentz, utilizandocuatro vectores: elde cuatro actual definido por
formado a partir de la densidad de corrientejy ρ densidad de carga, y laelectromagnética de cuatro potencial definido por
formado a partir del potencial vectorAy el potencial escalar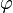 .La ecuación único resultante, debido aArnold Sommerfeld, una generalización de una ecuación debido aBernhard Riemanny conocida como la ecuación de Riemann-Sommerfeld o la forma covariante de las ecuaciones de Maxwell, es:
.La ecuación único resultante, debido aArnold Sommerfeld, una generalización de una ecuación debido aBernhard Riemanny conocida como la ecuación de Riemann-Sommerfeld o la forma covariante de las ecuaciones de Maxwell, es:
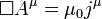 ,
,
donde 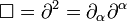 es el d'Alembert operador o cuatro Laplaciano,
es el d'Alembert operador o cuatro Laplaciano,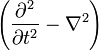 a veces escriben
a veces escriben O
O 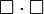 , Donde
, Donde  es el cuatro degradado.
es el cuatro degradado.
Formulaciones diferenciales
En espacio libre, donde ε = ε 0 y μ = μ 0 son constantes en todas partes, las ecuaciones de Maxwell simplificar considerablemente una vez que el lenguaje de la geometría diferencial y se utiliza formas diferenciales. En lo que sigue, unidades cgs-Gaussianos, no se utilizan unidades SI. (Para convertir a la SI, ver aquí.) Los campos eléctricos y magnéticos se describen conjuntamente por un 2-forma F en 4 dimensiones colector de espacio-tiempo. Las ecuaciones de Maxwell y luego reducir a la identidad de Bianchi
donde d denota laderivada exterior - coordenadas natural y métrica operador diferencial independiente que actúe en forma - y la ecuación de la fuente
donde el (dual)operador estrella Hodge * es una transformación lineal desde el espacio de 2 formas para el espacio de (4-2) -formas definida por la métrica enel espacio de Minkowski (en cuatro dimensiones incluso por cualquier métricaconformal a esta métrica ), y los campos están enunidades naturales donde 1 / 4πvarepsilon 0= 1. En este caso, la 3-forma deJse llama laforma de corriente eléctricao corriente-forma 3que satisface laecuación de continuidad
La corriente de forma 3 se puede integrar sobre una región de espacio-tiempo 3-dimensional. La interpretación física de esta integral es la carga en esa región si es spacelike, o la cantidad de carga que fluye a través de una superficie en una cierta cantidad de tiempo si esa región es una superficie spacelike cruzar un intervalo de tipo temporal. Como la derivada exterior se define en cualquier colector , la versión de forma diferencial de la identidad Bianchi tiene sentido para cualquier colector de 4-dimensional, mientras que la ecuación de origen se define si se orienta el colector y tiene una métrica de Lorentz. En particular, la versión de forma diferencial de las ecuaciones de Maxwell son una formulación conveniente e intuitiva de las ecuaciones de Maxwell en la relatividad general.
En una lineal, la teoría macroscópica, la influencia de la materia en el campo electromagnético se describe a través de transformación lineal más general en el espacio de 2-formas. Llamamos
la transformación constitutiva. El papel de esta transformación es comparable a la transformación dualidad Hodge. Las ecuaciones de Maxwell en la presencia de materia se convierten entonces en:
donde el 3-forma actualJsigue cumpliendo la continuidad ecuación dJ= 0.
Cuando los campos se expresan como combinaciones lineales (deproductos exterior) de base formulariosθp,
la relación constitutiva toma la forma
donde las funciones de coeficientes de campo son antisimétrico en los índices y los coeficientes son constitutivos antisimétrico en los pares correspondientes. En particular, la transformación dualidad Hodge que conduce a las ecuaciones de vacío discutidos anteriormente se obtienen tomando
que hasta la escala es el único tensor invariante de este tipo que se puede definir con la métrica.
En esta formulación, el electromagnetismo generaliza inmediatamente a cualquier variedad orientada 4-dimensional o con pequeñas adaptaciones cualquier colector, que no requieren incluso una métrica. Así, la expresión de las ecuaciones de Maxwell en términos de formas diferenciales conduce a una simplificación de notación y conceptual más. Mientras que las ecuaciones de Maxwell se podrían escribir como dos ecuaciones tensoriales en lugar de ocho ecuaciones escalares, de las que la propagación de las perturbaciones electromagnéticas y la ecuación de continuidad se podrían derivar con un poco de esfuerzo, utilizando formas diferenciales conduce a una derivación aún más simple de estos resultados.
Visión conceptual de esta formulación
En el lado conceptual, desde el punto de vista de la física, esto demuestra que las segunda y tercera ecuaciones de Maxwell deben agruparse juntos, ser llamado los homogéneos, y ser vistos como geométrico identidades que expresan otra cosa que: el campo F se deriva de una más "fundamental" potencial A . Mientras que la primera y la última debe ser visto como las dinámico ecuaciones de movimiento , obtenidos a través del principio de Lagrange de mínima acción, desde el "término de interacción" AJ (introducido a través de calibre derivadas covariantes), el acoplamiento del campo a la materia.
A menudo, la derivada de tiempo en la tercera ley motiva llamando esta ecuación "dinámica", que es algo engañoso; en el sentido del análisis precedente, esto es más bien un artefacto de romper relativista covarianza por la elección de una dirección de tiempo preferido. Para tener títulos físicos de libertad propagada por estas ecuaciones de campo, se debe incluir un término cinético F * F para A ; y tienen en cuenta los grados no físicos de la libertad que se pueden eliminar mediante la transformación de calibre A → A ' = A -. dα Ver también medir fijación y Faddeev-Popov fantasmas.
Geometric Algebra (GA) Formulación
En álgebra geométrica, las ecuaciones de Maxwell se reducen a una sola ecuación,
dondeFyJson multivectores
y
con la unidad depseudoescalarI 2= -1
El GA operador gradiente espacial∇actúa en un campo de vectores, de tal manera que
En álgebra espacio-tiempo usando el mismo producto geométrica de la ecuación es simplemente
el derivado de espacio-tiempo del campo electromagnético es su fuente. Aquí el (no negrita) gradiente de espacio-tiempo
es un vector de cuatro, como es la densidad de corriente
Para una demostración de que las ecuaciones dadas reproducen las ecuaciones de Maxwell ver el artículo principal.
Electrodinámica clásica como la curvatura de un haz de línea
Una forma elegante e intuitiva para formular las ecuaciones de Maxwell es el uso de complejos paquetes de línea o haces principales con fibra de U (1). La conexión  sobre el haz de línea tiene una curvatura
sobre el haz de línea tiene una curvatura 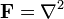 que es un dos-forma que satisfaga de forma automática
que es un dos-forma que satisfaga de forma automática 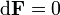 y se pueden interpretar como una intensidad de campo . Si el paquete de la línea es trivial con conexión de referencia plana d podemos escribir
y se pueden interpretar como una intensidad de campo . Si el paquete de la línea es trivial con conexión de referencia plana d podemos escribir 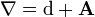 y F = d A con A la 1-forma integrada por el potencial eléctrico y el potencial vector magnético.
y F = d A con A la 1-forma integrada por el potencial eléctrico y el potencial vector magnético.
En la mecánica cuántica, la propia conexión se utiliza para definir la dinámica del sistema. Esta formulación permite una descripción natural del efecto Aharonov-Bohm. En este experimento, un campo magnético estático se ejecuta a través de un alambre magnético de largo (por ejemplo, un alambre de hierro magnetizado longitudinalmente). Fuera de este alambre de la inducción magnética es cero, en contraste con el potencial vector, que depende esencialmente de la del flujo magnético a través de la sección transversal del alambre y no desaparece exterior. Puesto que no hay campo eléctrico o bien, el tensor de Maxwell F = 0 en toda la región de espacio-tiempo fuera del tubo, durante el experimento. Esto significa por definición que la conexión  es plana allí.
es plana allí.
Sin embargo, como se ha mencionado, la conexión depende del campo magnético a través del tubo desde el holonomía a lo largo de una curva no contráctil que rodea el tubo es el flujo magnético a través del tubo en las unidades apropiadas. Esto puede ser detectada cuánticamente con un experimento de la doble rendija de difracción de electrones en una onda de electrones viajando alrededor del tubo. El holonomía corresponde a un desplazamiento de fase adicional, que conduce a un cambio en el patrón de difracción.
Espacio-tiempo curvo
Formulación tradicional
La materia y la energía generan curvatura de espacio tiempo. Este es el tema de la relatividad general . La curvatura del espacio-tiempo afecta la electrodinámica. Un campo electromagnético que tiene energía y el momento también genera la curvatura del espacio-tiempo. Las ecuaciones de Maxwell en el espacio-tiempo curvo se pueden obtener mediante la sustitución de los derivados en las ecuaciones en el espacio-tiempo plano con derivadas covariantes. las ecuaciones de origen y de código libre se convierten en ((Si esto es la generalización apropiada requiere una investigación independiente.) cgs-Gaussianos unidades):
y
Aquí,
es un Símbolo de Christoffel que caracteriza a la curvatura del espacio-tiempo y laDγes la derivada covariante.
Formulación en términos de formas diferenciales
La formulación de las ecuaciones de Maxwell en términos de formas diferenciales se puede utilizar sin cambio en la relatividad general. La equivalencia de la formulación relativista general, más tradicional usando la derivada covariante con la formulación de forma diferencial se puede ver como sigue. Elija coordenadas locales x α que da una base de 1-formas d x α en cada punto del conjunto abierto, donde se definen las coordenadas. El uso de esta base y unidades cgs-Gaussianos definimos
- El tensor de campo infinitesimal antisimétrica
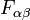 , correspondiente al campo 2-formaF
, correspondiente al campo 2-formaF
- La corriente vector infinitesimal 3-formaJ
Aquíges como siempre el determinante del tensor métrico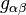 .Un pequeño cálculo que utiliza la simetría de lossímbolos de Christoffel (es decir, la torsión-refinado de laconexión de Levi Civita) y la constantness covariante deloperador estrella Hodge continuación, muestra que en esta coordenada barrio tenemos:
.Un pequeño cálculo que utiliza la simetría de lossímbolos de Christoffel (es decir, la torsión-refinado de laconexión de Levi Civita) y la constantness covariante deloperador estrella Hodge continuación, muestra que en esta coordenada barrio tenemos:
- la identidad Bianchi
- la ecuación fuente
- la ecuación de continuidad