Mecânica estatística
Informações de fundo
Esta seleção wikipedia foi escolhido por voluntários que ajudam Crianças SOS da Wikipedia para este Seleção Wikipedia para as escolas. Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.
| Mecânica estatística |
|---|
 |
|
Estatísticas de partículas
|
Ensembles
|
Modelos
|
Potenciais
|
Mecânica estatística é a aplicação da teoria da probabilidade , que inclui matemáticos ferramentas para lidar com grandes populações, ao campo de mecânica, que está relacionada com o movimento de partículas ou de objectos, quando submetido a uma força. Mecânica estatística, às vezes chamados física estatística, pode ser visto como um subcampo da física e da química .
Ele fornece uma estrutura para relacionar as propriedades microscópicas de átomos e moléculas individuais para as propriedades macroscópicas ou a granel de materiais que podem ser observados na vida cotidiana, portanto, explicando termodinâmica como um resultado natural de estatísticas e de mecânica (clássica e quântica) em nível microscópico . Em particular, ele pode ser usado para calcular as propriedades termodinâmicas dos materiais a granel a partir dos dados espectroscópicos de moléculas individuais.
Esta capacidade de fazer previsões com base nas propriedades macroscópicas microscópicas é a principal vantagem da mecânica estatística sobre termodinâmica . Ambas as teorias são regidos pela segunda lei da termodinâmica por meio da entropia . No entanto, a entropia em termodinâmica só pode ser conhecida empiricamente, enquanto que na mecânica estatística, é uma função da distribuição do sistema nas suas micro-estados.
Postulado fundamental
O postulado fundamental da mecânica estatística (também conhecida como a igualdade de um postulado probabilidade priori) é o seguinte:
- Dado um sistema isolado no equilíbrio, verificou-se com igual probabilidade em cada um dos seus acessível microestados.
Este postulado é um pressuposto fundamental em mecânica estatística - ele afirma que um sistema em equilíbrio não tem qualquer preferência por qualquer dos seus microestados disponíveis. Dado micro Ω com uma energia particular, a probabilidade de encontrar o sistema em particular é um micro p = 1 / Ω.
Este postulado é necessária porque permite concluir que, para um sistema em equilíbrio, o estado termodinâmico (macroestado) que poderia resultar do maior número de micro também é o macroestado mais provável do sistema.
O postulado é justificado, em parte, para sistemas clássicos, por O teorema de Liouville (Hamiltoniano), o que mostra que, se a distribuição de sistema de pontos através acessíveis espaço de fase é uniforme em algum momento, ele permanece assim em momentos posteriores.
Justificação semelhantes para um sistema discreto é fornecida pelo mecanismo de balanço detalhado.
Isto permite a definição da função de informações (no contexto de teoria da informação):
Quando todos rhos são iguais, eu é mínima, o que reflete o fato de que temos o mínimo de informação sobre o sistema. Quando nossa informação é máxima, ou seja, um ró é igual a um eo restante para zero (nós sabemos em que estado o sistema está em), a função é máxima.
Esta "função de informações" é a mesma que a função reduzida entrópica em termodinâmica.
Conjunto microcanónico
Em conjunto microcanónico N, V e E são fixos. Uma vez que a segunda lei da termodinâmica se aplica a sistemas isolados, o primeiro caso investigado corresponderá a este caso. O conjunto microcanónico descreve um sistema isolado.
A entropia de um tal sistema só pode aumentar, de modo a que o máximo da sua entropia corresponde a um estado de equilíbrio para o sistema.
Porque um isolado sistema mantém uma energia constante, o total de energia do sistema não flutua. Assim, o sistema pode acessar apenas aqueles dos seus micro-estados que correspondem a um determinado valor E da energia. O energia interna do sistema, em seguida, é exactamente igual à sua energia .
Chamemos 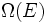 o número de micro-estados correspondentes a esse valor da energia do sistema. O estado macroscópica de máxima entropia para o sistema é aquela em que todos os micro-estados têm igual probabilidade de ocorrer, com probabilidade
o número de micro-estados correspondentes a esse valor da energia do sistema. O estado macroscópica de máxima entropia para o sistema é aquela em que todos os micro-estados têm igual probabilidade de ocorrer, com probabilidade 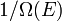 , Durante as flutuações do sistema.
, Durante as flutuações do sistema.
- onde
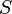 é o sistema de entropia ,
é o sistema de entropia , 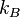 é Constante de Boltzmann
é Constante de Boltzmann
Conjunto canónico
Em conjunto canónico N, V e T são fixos. Invocar o conceito de conjunto canónico, é possível derivar a probabilidade 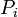 que um sistema macroscópico, em equilíbrio térmico com o seu ambiente, estará em um dado microstate com energia
que um sistema macroscópico, em equilíbrio térmico com o seu ambiente, estará em um dado microstate com energia 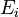 de acordo com Distribuição de Boltzmann:
de acordo com Distribuição de Boltzmann:
- onde
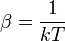 ,
,
A temperatura 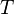 surge do facto de que o sistema está em equilíbrio térmico com o seu ambiente. As probabilidades das várias microestados deve adicionar a um, ea fator de normalização no denominador é o canônico função de partição:
surge do facto de que o sistema está em equilíbrio térmico com o seu ambiente. As probabilidades das várias microestados deve adicionar a um, ea fator de normalização no denominador é o canônico função de partição:
onde 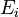 é a energia do
é a energia do 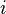 th microstate do sistema. A função de partição é uma medida do número de estados acessíveis para o sistema a uma dada temperatura. O artigo conjunto canónico contém uma derivação do fator de Boltzmann ea forma da função de partição dos primeiros princípios.
th microstate do sistema. A função de partição é uma medida do número de estados acessíveis para o sistema a uma dada temperatura. O artigo conjunto canónico contém uma derivação do fator de Boltzmann ea forma da função de partição dos primeiros princípios.
Para resumir, a probabilidade de encontrar um sistema à temperatura 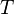 em um determinado estado com energia
em um determinado estado com energia 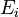 é
é
Conexão termodinâmico
A função de partição pode ser utilizado para encontrar o valor esperado (média) de qualquer propriedade microscópica do sistema, que pode então ser relacionado com variáveis macroscópicas. Por exemplo, o valor esperado da energia microscópica 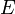 é interpretado como a definição microscópica da energia interna variável termodinâmica
é interpretado como a definição microscópica da energia interna variável termodinâmica 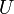 ., E pode ser obtida tomando a derivada da função de partição no que diz respeito à temperatura. Com efeito,
., E pode ser obtida tomando a derivada da função de partição no que diz respeito à temperatura. Com efeito,
implica, em conjunto com a interpretação de 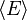 como
como 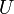 , A seguinte definição microscópica interno da energia:
, A seguinte definição microscópica interno da energia:
A entropia pode ser calculada por (ver Shannon entropia)
o que implica que
é o energia livre do sistema ou em outras palavras,
Tendo expressões microscópicas para os potenciais termodinâmicos básicos 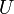 ( energia interna),
( energia interna), 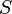 ( entropia ) e
( entropia ) e 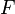 ( energia livre) é suficiente para derivar expressões para outras grandezas termodinâmicas. A estratégia básica é a seguinte. Pode haver uma quantidade intensivas ou extensivas que entra explicitamente na expressão para a energia microscópica
( energia livre) é suficiente para derivar expressões para outras grandezas termodinâmicas. A estratégia básica é a seguinte. Pode haver uma quantidade intensivas ou extensivas que entra explicitamente na expressão para a energia microscópica 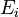 , Por exemplo campo magnético (intensivo) ou volume (extensa). Em seguida, as variáveis termodinâmicas conjugadas são derivados da energia interna. A magnetização macroscópica (extensa) é o derivado de
, Por exemplo campo magnético (intensivo) ou volume (extensa). Em seguida, as variáveis termodinâmicas conjugadas são derivados da energia interna. A magnetização macroscópica (extensa) é o derivado de 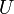 no que diz respeito ao (intensivo) campo magnético, e a pressão (intensivo) é o derivado de
no que diz respeito ao (intensivo) campo magnético, e a pressão (intensivo) é o derivado de 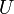 com respeito ao volume (grande).
com respeito ao volume (grande).
O tratamento desta seção não assume qualquer troca de matéria (massa ou seja fixa e número de partículas fixas). No entanto, o volume do sistema é variável o que significa que a densidade também é variável.
Esta probabilidade pode ser utilizado para encontrar o valor médio, o que corresponde ao valor macroscópica, de qualquer propriedade, 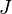 , Que depende do estado energético do sistema por meio da seguinte fórmula:
, Que depende do estado energético do sistema por meio da seguinte fórmula:
onde 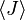 é o valor médio da propriedade
é o valor médio da propriedade 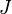 . Esta equação pode ser aplicada para a energia interna,
. Esta equação pode ser aplicada para a energia interna, 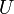 :
:
Subsequentemente, estas equações podem ser combinados com relações conhecidas entre termodinâmicas 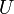 e
e 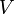 para chegar a uma expressão para a pressão apenas em termos de temperatura, volume e a função de partição. Relações semelhantes em termos da função de partição pode ser derivado para outras propriedades termodinâmicas, como mostrado na tabela a seguir; ver também a explicação detalhada no configuração integral.
para chegar a uma expressão para a pressão apenas em termos de temperatura, volume e a função de partição. Relações semelhantes em termos da função de partição pode ser derivado para outras propriedades termodinâmicas, como mostrado na tabela a seguir; ver também a explicação detalhada no configuração integral.
| Helmholtz energia livre: | 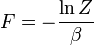 |
|---|---|
| Interno da energia: |  |
| Pressão: | 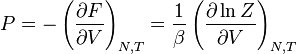 |
| Entropia : | 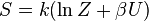 |
| Gibbs energia livre : |  |
| Entalpia : | 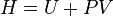 |
| Volume constante capacidade de calor: | 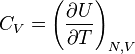 |
| Constante capacidade de calor de pressão: | 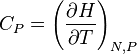 |
| Potencial químico: | 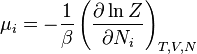 |
Para clarificar, este não é um grande conjunto canónico.
Muitas vezes, é útil considerar a energia de uma determinada molécula a ser distribuído entre vários modos. Por exemplo, a energia translacional refere-se àquela porção de energia associado com o movimento do centro de massa da molécula. Energia configuracional refere-se àquela porção de energia associado com as várias forças atractivas e repulsivas entre as moléculas de um sistema. Os outros modos são todos considerados interno para cada molécula. Eles incluem os modos de rotação, vibração, eletrônicos e nucleares. Se assumirmos que cada um dos modos é (a suposição questionável) independente da energia total pode ser expressa como a soma de cada um dos componentes:
Quando os subscritos 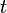 ,
,  ,
,  ,
,  ,
,  E
E 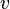 correspondem a translacional, configurational, nuclear, modos eletrônicos, rotacionais e vibracionais, respectivamente. A relação em esta equação pode ser substituído na primeira equação para dar:
correspondem a translacional, configurational, nuclear, modos eletrônicos, rotacionais e vibracionais, respectivamente. A relação em esta equação pode ser substituído na primeira equação para dar:
Se podemos assumir todos estes modos são completamente desacoplado e não correlacionadas, então todos esses fatores são, em certo sentido probabilidade completamente independente, em seguida,
Assim, uma função de partição pode ser definido para cada modo. As expressões simples foram derivados relativa de cada um dos vários modos para vários propriedades moleculares mensuráveis, tais como as frequências de rotação ou vibracionais característicos.
Expressões para as várias funções de partição moleculares estão apresentados na tabela a seguir.
| Nuclear | 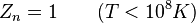 |
|---|---|
| Eletrônico | 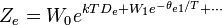 |
| Vibracional |  |
| Rotacional (linear) | 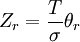 |
| Rotacional (não-linear) | 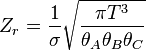 |
| Translational | 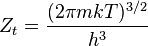 |
| Configuracional (gás ideal) | 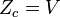 |
Essas equações podem ser combinados com os da primeira tabela para determinar a contribuição de um modo particular da energia a uma propriedade termodinâmica. Por exemplo, a "pressão rotacional" pode ser determinada deste modo. A pressão total poderia ser encontrado pela soma das contribuições de pressão de todos os modos individuais, ou seja:
Grande conjunto canónico
Em grande canônico conjunto V, T e potencial químico são fixos. Se o sistema em estudo é um sistema aberto, (matéria pode ser trocado), mas o número de partículas não é conservada, teríamos de introduzir potenciais químicos, μ j, j = 1, ..., n e substituir o canónica função de partição com o grande função de partição canónica:
onde N ij é o número de ordem j partículas de espécies na ordem i configuração. Às vezes, temos também outras variáveis que contribuem para o função de partição, um correspondente a cada quantidade conservada. A maioria deles, no entanto, pode ser interpretado de forma segura como potenciais químicos. Na maioria dos sistemas de matéria condensada, as coisas são não-relativística e massa é conservada. No entanto, a maioria dos sistemas de matéria condensada de interesse também conservar o número de partículas aproximadamente (metastably) ea massa (nonrelativistically) não é outro senão a soma do número de cada tipo de partícula vezes a sua massa. Massa está inversamente relacionada com a densidade, que é a variável conjugado à pressão. Para o restante deste artigo, vamos ignorar essa complicação e fingir potenciais químicos, não importa. Ver grande conjunto canónico.
Vamos refazer tudo usando um conjunto canónico grande neste momento. O volume é deixado fixo e não figura na em todo este tratamento. Como antes, j é o índice das partículas de espécies j e i é o índice de microstate i:
| Grande potencial: | 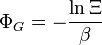 |
| Interno da energia: | 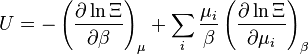 |
| Número de partículas: | 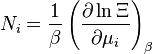 |
| Entropia : | 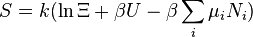 |
| Energia livre de Helmholtz: | 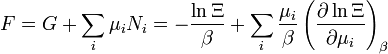 |
Equivalência entre as descrições no limite termodinâmico
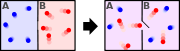
Todas as descrições acima diferem na maneira de permitir que o sistema dado a flutuar entre as suas configurações.
No conjunto de micro-canônico, as trocas sistema de energia não com o mundo exterior, e não é, portanto, sujeitos a flutuações de energia, enquanto que no conjunto canónico, o sistema é livre para trocar energia com o exterior sob a forma de calor .
No limite termodinâmico, que é o limite de grandes sistemas, as flutuações tornam-se insignificante, de modo que todas estas descrições convergem para a mesma descrição. Em outras palavras, o comportamento de um sistema macroscópico não dependem do conjunto particular usado para a sua descrição.
Dadas estas considerações, o melhor conjunto de escolher para o cálculo das propriedades de um sistema macroscópico é esse conjunto que permite que o resultado mais facilmente ser derivada.
Caminhantes aleatórios
O estudo de cadeia longa polímeros tem sido uma fonte de problemas dentro dos domínios da mecânica estatística já que cerca de 1950. Uma das razões pelas quais os cientistas, contudo, que estavam interessados no estudo é que as equações que governam o comportamento de uma cadeia de polímero foram independentes da cadeia química. O que é mais, a equação governante acaba por ser um passeio aleatório (difusora) e no espaço. De fato, a equação de Schrödinger é em si uma equação de difusão em tempo imaginário, 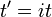 .
.
Passeios aleatórios no tempo
O primeiro exemplo de um passeio aleatório é um no espaço, através do qual uma partícula passa por um movimento aleatório, devido a forças externas no seu meio circundante. Um exemplo típico seria um grão de pólen num copo de água. Se fosse possível algum modo "tingir" o caminho do grão de pólen tenha tomado, o caminho é definido como observado um passeio aleatório.
Considere um problema de brinquedo, de um trem em movimento ao longo de uma faixa 1D na direção-x. Suponha-se que o comboio se move quer uma distância de + ou - b uma distância fixa, dependendo se uma moeda cair cara ou coroa quando invertida. Vamos começar por considerar as estatísticas dos passos que o trem de brinquedo leva (onde 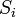 é o passo om tomadas):
é o passo om tomadas):
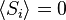 ; devido a priori probabilidades iguais
; devido a priori probabilidades iguais 
A segunda quantidade é conhecida como a função de correlação. A delta é a delta de Kronecker que nos diz que, se os índices i e j são diferentes, então o resultado é 0, mas se i = j, em seguida, o delta de Kronecker é 1, de modo que o função de correlação retorna um valor de 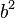 . Isso faz sentido, porque se i = j, então estamos considerando o mesmo passo. Em vez trivialmente então ele pode ser mostrado que a deslocação média do comboio no eixo dos x é 0;
. Isso faz sentido, porque se i = j, então estamos considerando o mesmo passo. Em vez trivialmente então ele pode ser mostrado que a deslocação média do comboio no eixo dos x é 0;
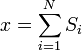
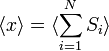
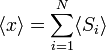
Como afirmado 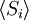 é 0, então a soma de 0 ainda é 0. Também pode ser mostrado, utilizando o mesmo método demonstrado acima, para calcular o valor médio quadrático da problema. O resultado deste cálculo é dado abaixo
é 0, então a soma de 0 ainda é 0. Também pode ser mostrado, utilizando o mesmo método demonstrado acima, para calcular o valor médio quadrático da problema. O resultado deste cálculo é dado abaixo
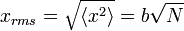
Do equação de difusão que pode ser mostrado que a distância de difusão de uma partícula se move em um meio é proporcional à raiz do momento em que o sistema foi difusão para, onde a constante de proporcionalidade, é a raiz da constante de difusão. A relação acima, embora cosmeticamente diferente revela física semelhante, em que N é simplesmente o número de passos movidos (é frouxamente ligado com o tempo) e b é o comprimento do passo característica. Como conseqüência, podemos considerar como um processo de difusão de passeio aleatório.
Passeios aleatórios no espaço
Passeios aleatórios no espaço pode ser pensado como snapshots do caminho tomado por um caminhante aleatório no tempo. Um tal exemplo é a configuração espacial de polímeros de cadeia longa.
Existem dois tipos de passeio aleatório no espaço: auto-evitando passeios aleatórios, onde os elos da cadeia de polímero interagem e não se sobrepõem no espaço, e passeios aleatórios puros, onde os elos da cadeia de polímero são não-interagindo e ligações são livres para deitar em cima um do outro. O primeiro tipo é mais aplicável aos sistemas físicos, mas suas soluções são mais difíceis de obter pelo dos primeiros princípios.
Ao considerar um livremente articulado, não interagindo cadeia de polímero, o vector de extremidade-a-extremidade está 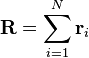 onde
onde 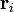 é a posição do vector de ligação -ésimo i na cadeia. Como resultado do teorema do limite central, se N >> 1, então o que esperamos uma distribuição de Gauss para o vetor end-to-end. Nós também podemos fazer declarações das estatísticas dos próprios links;
é a posição do vector de ligação -ésimo i na cadeia. Como resultado do teorema do limite central, se N >> 1, então o que esperamos uma distribuição de Gauss para o vetor end-to-end. Nós também podemos fazer declarações das estatísticas dos próprios links; 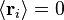 ; por a isotropia do espaço
; por a isotropia do espaço 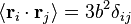 ; todos os elos da cadeia não estão correlacionadas com o outro
; todos os elos da cadeia não estão correlacionadas com o outro
Usando as estatísticas dos links individuais, é facilmente demonstrado que 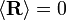 e
e 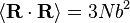 . Observe este último resultado é a mesma que foi encontrada para passeios aleatórios no tempo.
. Observe este último resultado é a mesma que foi encontrada para passeios aleatórios no tempo.
Assumindo, como foi dito, que a referida distribuição de vectores de ponta a ponta para um muito grande número de cadeias de polímero idênticas é Gaussiana, a distribuição de probabilidade tem a seguinte forma
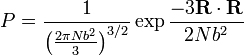
Para que serve isso conosco? Recorde-se que de acordo com o princípio da igualmente susceptíveis probabilidades a priori, o número de micro, Ω, em algum valor físico é directamente proporcional à distribuição de probabilidade em que o valor físico, a saber;
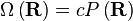
onde C é uma constante de proporcionalidade arbitrária. Dada a nossa função de distribuição, existe uma máxima que corresponde a 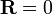 . Fisicamente este ascende à existência de mais micro que têm um vector de ponta a ponta de 0 microstate do que qualquer outro. Agora, considerando
. Fisicamente este ascende à existência de mais micro que têm um vector de ponta a ponta de 0 microstate do que qualquer outro. Agora, considerando 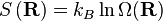

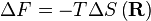
em que F é a Energia livre de Helmholtz é trivial para mostrar que 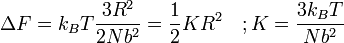
Uma mola Hookian!
Este resultado é conhecido como a Primavera Entropic Resultado e equivale a dizer que, ao esticar uma cadeia de polímero que você está fazendo um trabalho sobre o sistema de arrastá-lo longe de seu estado de equilíbrio (de preferência). Um exemplo disto é uma banda elástica comum, composto por (de borracha) polímeros de cadeia longa. Ao esticar o elástico que você está fazendo um trabalho sobre o sistema ea banda se comporta como uma mola convencional. O que é especialmente surpreendente sobre este resultado no entanto, é que o trabalho realizado no alongamento da cadeia de polímero pode ser totalmente relacionada com a alteração da entropia do sistema como um resultado do estiramento.

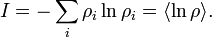
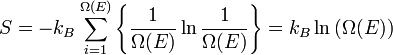
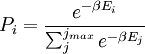
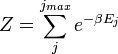
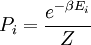
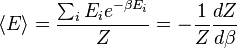

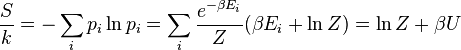
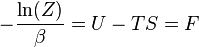
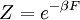
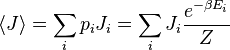
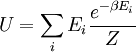
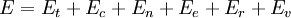

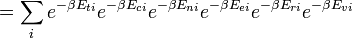
![\ Xi (V, T, \ mu) = \ sum_i \ exp \ left (\ beta \ left [\ sum_ {j = 1} ^ n \ mu_j N_ {ij} -E_i \ right] \ right)](../../images/633/63360.png)