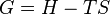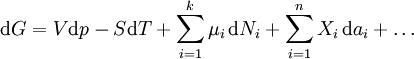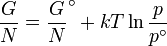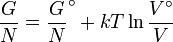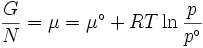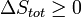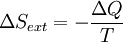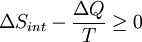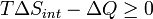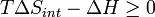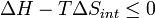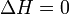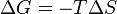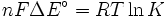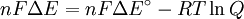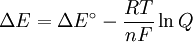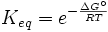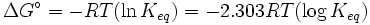Gibbs energia livre
Sobre este escolas selecção Wikipedia
Crianças SOS produziu este website para as escolas, bem como este site de vídeo sobre a África . Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?
| Mecânica estatística |
|---|
 |
|
Estatísticas de partículas
|
Ensembles
|
|
Modelos
|
Potenciais
|
Em termodinâmica , a energia livre de Gibbs ( IUPAC nome recomendado: Gibbs energia ou função Gibbs) é uma potencial termodinâmica que mede o "útil" ou de iniciação processo de trabalho obtido a partir de um isotérmico, isobaric sistema termodinâmico. Tecnicamente, a energia livre de Gibbs é a quantidade máxima de trabalho não-expansão que pode ser extraído a partir de um sistema fechado ou esta máxima só pode ser alcançado em um completamente processo reversível. Quando um sistema muda de um estado inicial bem definida para um estado final bem definida, a energia livre de Gibbs ΔG é igual ao trabalho trocado por o sistema com a sua envolvente, menos o trabalho das forças de pressão, durante uma transformação reversível do sistema a partir do mesmo estado inicial para o mesmo estado final.
Gibbs energia é também o potencial químico que é minimizada quando o sistema atinja o equilíbrio de temperatura e a uma pressão constante. Como tal, é um critério conveniente de espontaneidade para processos com pressão e temperatura constante.
A energia livre de Gibbs, originalmente chamado de energia disponível, foi desenvolvido em 1870 pelo físico matemático americano Willard Gibbs . Em 1873, em uma nota de rodapé, Gibbs definiu o que ele chamou de "energia disponível" de um corpo como tal:
| " | A maior quantidade de trabalho mecânico que pode ser obtido a partir de uma determinada quantidade de uma determinada substância em um determinado estado inicial, sem aumentar seu total de volume ou permitindo que o calor para passar para ou a partir de organismos externos, exceto como no encerramento dos processos são deixou em sua condição inicial. | " |
O estado inicial do corpo, de acordo com Gibbs, deve ser tal que 'o corpo pode ser feito passar para a partir dele para estados de energia dissipada por processos reversíveis ". Em seu 1876 magnum opus Sobre o Equilíbrio de Substâncias heterogêneas, uma análise gráfica de sistemas químicos multi-fase, ele se envolveu seus pensamentos sobre energia livre química na íntegra.
Definições
A energia livre de Gibbs é definido como:
que é o mesmo que:
onde:
- U é a energia interna ( Unidade SI: joule)
- p é pressão (unidade SI: pascal)
- V é o volume (Unidade SI: m 3)
- T é a temperatura (unidade SI: kelvin )
- S é a entropia (unidade SI: joule por kelvin)
- H é a entalpia (unidade SI: joule)
A expressão para a mudança reversível infinitesimal na energia livre de Gibbs, para um sistema aberto, submetido à operação de forças externas i X, que fazem com que os parâmetros externos do sistema, um i para mudar de um montante da I, é dada por:
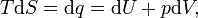 onde:
onde:
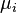 é o potencial químico da i-ésima componente químico. (Unidade SI: joules por partículas ou joules por mol)
é o potencial químico da i-ésima componente químico. (Unidade SI: joules por partículas ou joules por mol) 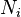 é o número de partículas (ou número de moles) que compõem o i -ésimo componente químico.
é o número de partículas (ou número de moles) que compõem o i -ésimo componente químico.
Esta é uma forma de Gibbs equação fundamental. Na expressão infinitesimal, o termo envolvendo as eventuais contas de químicos para mudanças na energia livre de Gibbs resultantes de um afluxo ou outflux de partículas. Em outras palavras, ela vale para um sistema aberto. Para sistema fechado, este prazo pode ser descartado.
Qualquer número de termos adicionais podem ser adicionados, dependendo do sistema particular a ser considerada. Além de trabalho mecânico , um sistema pode, além disso executar vários outros tipos de trabalho. Por exemplo, na expressão infinitesimal, a energia de trabalho contráctil associado com um sistema termodinâmico que é uma fibra contráctil que encurta por uma quantidade - dl sob uma força f resultaria numa fdl termo que está sendo adicionado. Se uma quantidade de carga - de é adquirido por um sistema a uma Ψ potencial eléctrico, o trabalho eléctrico associado com esta é de -Ψ, que seria incluído na expressão infinitesimal. Outros termos de trabalho são adicionados por requisitos de sistema.
Cada quantidade nas equações acima podem ser divididas pela quantidade de substância, medido em moles, para formar Gibbs energia livre molar. A energia livre de Gibbs é uma das funções termodinâmicas mais importantes para a caracterização de um sistema. É um factor nos resultados que determinam como o tensão de um célula electroquímica, e o constante de equilíbrio para uma reacção reversível. Em isotérmica, sistemas isobáricas, energia livre de Gibbs pode ser pensado como uma quantidade "dinâmico", na medida em que é uma medida representativa dos efeitos concorrentes das forças de entalpia e entropia de condução envolvidas num processo termodinâmico.
A dependência da temperatura da energia de Gibbs para uma gás ideal é dada pela Gibbs-Helmholtz equação e a sua dependência da pressão é dado por:
Se o volume é conhecido, em vez de pressão, em seguida, torna-se:
ou, mais convenientemente como o seu potencial químico:
Em sistemas não-ideal, fugacidade entra em jogo.
Derivação
A energia livre de Gibbs diferencial total em termos da sua variáveis naturais pode ser derivada através Legendre transforma do energia interna. Para um sistema em processo internamente reversível que é permitido trocar a matéria, calor e trabalho com os seus arredores, o diferencial da energia interna é dada a partir da primeira lei da termodinâmica como
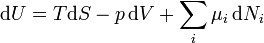 .
.
Porque 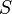 ,
, 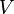 E
E 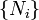 são variáveis extensivas, Teorema da função homogênea de Euler permite fácil integração de
são variáveis extensivas, Teorema da função homogênea de Euler permite fácil integração de 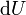 :
:
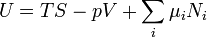 .
.
A definição de 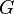 a partir de cima é
a partir de cima é
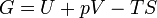 .
.
Tomando o diferencial total, temos
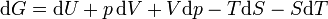 .
.
Substituindo 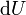 com o resultado da primeira lei dá
com o resultado da primeira lei dá
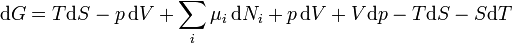
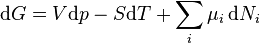 .
.
As variáveis naturais 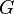 são então
são então 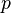 ,
, 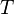 E
E 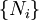 . Porque algumas das variáveis naturais são intensivos,
. Porque algumas das variáveis naturais são intensivos, 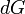 não podem ser integrados utilizando integrais de Euler como é o caso com a energia interna. No entanto, simplesmente substituindo o resultado para
não podem ser integrados utilizando integrais de Euler como é o caso com a energia interna. No entanto, simplesmente substituindo o resultado para 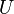 na definição de
na definição de 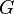 dá uma expressão padrão para G:
dá uma expressão padrão para G:
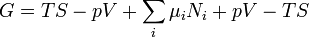
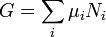 .
.
Visão global
De uma forma simples, no que diz respeito a STP sistemas de reagir, um general regra de ouro é:
| " | Todo sistema procura alcançar um mínimo de energia livre. | " |
Assim, fora desta tendência natural geral, uma medida quantitativa de como perto ou de longe uma reação potencial é a partir desta mínimo é quando a energética calculados do processo indicam que a mudança na energia livre de Gibbs ΔG é negativo. Essencialmente, isto significa que uma tal reacção será favorecida e libertar energia. A energia libertada é igual à quantidade máxima de trabalho que pode ser realizado como um resultado da reacção química. Por outro lado, se as condições indicadas uma ΔG positiva, então a energia - sob a forma de trabalho - teria de ser adicionado ao sistema de reacção para realizar a reacção de ir.
História
A quantidade chamada "energia livre" é essencialmente um substituto mais avançado e preciso para o termo ultrapassado " afinidade ", que foi usado por químicos em anos anteriores para descrever a" força "que causou reações químicas . A afinidade de termo, como utilizado em relação química, remonta a, pelo menos, o tempo de Albertus Magnus em 1250.
A partir de 1998 os livros didáticos modernos Termodinâmica pelo Prêmio Nobel e professor de engenharia química Ilya Prigogine encontramos:? "Como o movimento foi explicada pelo conceito newtoniano de força, os químicos queria um conceito semelhante de" força motriz "para a mudança química Por que as reações químicas ocorrem, e por que eles param em determinados pontos químicos chamado de ' força "que causou afinidade reações químicas, mas faltava uma definição clara".
Durante todo o século 18, a visão dominante em relação ao calor e luz que foi apresentada por Isaac Newton , chamada de "hipótese newtoniana", que afirmava que a luz eo calor são formas de matéria atraídos ou repelidos por outras formas de matéria, com forças de gravitação ou análogos para a afinidade química.
No século 19, o químico francês Marcellin Berthelot eo químico dinamarquês Julius Thomsen tentou quantificar afinidade utilizando calores de reação. Em 1875, após a quantificação dos calores de reacção para um grande número de compostos, Berthelot proposto o " princípio de trabalho máximo "em que todas as mudanças químicas que ocorrem sem a intervenção de energia fora tendem para a produção de corpos ou de um sistema de corpos que libertam calor .
Além disso, em 1780, Antoine Lavoisier e Pierre-Simon Laplace lançou as bases da termoquímica, mostrando que o calor emitido numa reacção é igual ao calor absorvido na reacção inversa. Eles também investigou o calor específico e calor latente de uma série de substâncias, e quantidades de calor dadas para fora em combustão. Da mesma forma, em 1840 o químico suíço Germain Hess formulado o princípio de que a libertação de calor numa reacção é o mesmo se o processo é realizado em uma única etapa ou em uma série de etapas. Isto é conhecido como Lei de Hess. Com o advento da teoria mecânica do calor no início do século 19, a lei de Hess passou a ser visto como uma consequência da lei de conservação de energia.
Com base nestes e outras ideias, Berthelot e Thomsen, bem como outros, considerado o calor emitido na formação de um composto tal como uma medida da afinidade, ou o trabalho realizado pelas forças químicas. Essa visão, no entanto, não estava inteiramente correta. Em 1847, o físico Inglês James Joule mostrou que ele pode elevar a temperatura da água, rodando uma roda de pás nele, mostrando, assim, que o calor e trabalho mecânico foram equivalentes ou proporcionais entre si, isto é, aproximadamente, 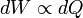 . Esta declaração veio a ser conhecido como o equivalente mecânico do calor e era uma forma precursora da primeira lei da termodinâmica .
. Esta declaração veio a ser conhecido como o equivalente mecânico do calor e era uma forma precursora da primeira lei da termodinâmica .
Em 1865, o físico alemão Rudolf Clausius tinha mostrado que este princípio de equivalência necessária alteração. Ou seja, pode-se usar o calor a partir de um derivado reação de combustão em um forno de carvão para ferver a água, e usar esse calor para vaporizar a vapor e, em seguida, usar a energia de alta pressão melhorada do vapor vaporizado para empurrar um pistão. Assim, poderíamos ingenuamente argumentar que se pode converter inteiramente o calor de combustão inicial da reação química para o trabalho de empurrar o pistão. Clausius mostrou, no entanto, que é preciso levar em conta o trabalho que as moléculas do corpo de trabalho, ou seja, as moléculas de água no cilindro, fazer uns sobre os outros como eles passam ou transformar a partir de um passo de ou Estado da ciclo do motor para a outra, por exemplo, a partir de (P1, V1) a (P2, V2). Clausius originalmente chamou isso de "conteúdo transformação" do corpo, e mais tarde mudou o nome para a entropia . Assim, o calor utilizado para transformar o corpo de trabalho de moléculas a partir de um estado para o outro não pode ser usado para fazer o trabalho externa, por exemplo, para apertar o êmbolo. Clausius definido este calor transformação como dQ = TdS.
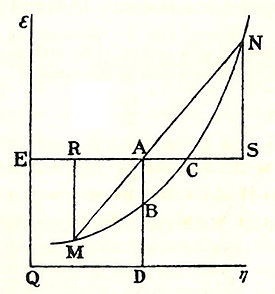
Em 1873, Willard Gibbs publicou um método de representação geométrica das propriedades termodinâmicas de substâncias por meio de superfícies em que ele introduziu o primeiro esboço dos princípios da sua nova equação capazes de prever ou estimar as tendências de vários processos naturais de acontecer quando os corpos ou sistemas são postos em contacto. Ao estudar as interações de substâncias homogéneas em contacto, ou seja, órgãos, sendo em parte composição sólida, líquida parte, e parte do vapor, e usando um tridimensional de volume - entropia - gráfico interno da energia, Gibbs foi capaz de determinar três estados de equilíbrio, ou seja, "necessariamente estável", "neutro", e "instável", e se ou não mudanças irão acontecer. Em 1876, Gibbs construída sobre este quadro, introduzindo o conceito de potencial químico de modo a ter em conta as reacções químicas e estados de organismos que sejam quimicamente diferentes um do outro. Em suas próprias palavras, para resumir seus resultados em 1873, Gibbs afirma:
Nesta descrição, como o usado por Gibbs, refere-se à ε energia interna do corpo, η refere-se a entropia do corpo, e é a ν o volume do corpo.
Assim, em 1882, após a introdução desses argumentos por Clausius e Gibbs, o cientista alemão Hermann Von Helmholtz indicado, em oposição a Berthelot e Thomas 'hipótese de que a afinidade química é uma medida do calor de reacção da reacção química como com base no princípio de trabalho máxima, que a afinidade não é o dado de calor na formação de um composto mas pelo contrário, é a maior quantidade de trabalho que pode ser adquirida quando a reacção é levada a cabo de um modo reversível, por exemplo, trabalho eléctrica numa célula reversível. O trabalho máxima é, assim, considerada como a diminuição do livre, ou disponíveis, a energia do sistema (Gibbs energia livre G em T = constante, P = constante ou energia livre de Helmholtz F em T = constante, V = constante), enquanto que o calor que é transmitida é geralmente uma medida da diminuição da energia total do sistema ( Energia interna). Assim, G ou M é a quantidade de energia "livre" para trabalhar sob as condições dadas.
Até este ponto, a vista geral havia sido de tal forma que: "todas as reacções químicas conduzir o sistema para um estado de equilíbrio em que as afinidades dos reacções desaparecem". Durante os próximos 60 anos, a afinidade termo passou a ser substituído com a energia livre de termo. De acordo com a química historiador Henry Leicester, o influente livro de 1923 Termodinâmica e Energia Livre de reações químicas por Gilbert N. Lewis e Merle Randall levou à substituição do termo "afinidade" pelo termo "energia livre" em grande parte do mundo de fala Inglês.
O que significa o termo "livre" significa?
Nos séculos 18 e 19, o teoria do calor, ou seja, que o calor é uma forma de energia com relação ao movimento vibratório, estava começando a suplantar tanto o teoria calórica, isto é que o calor é um fluido, e o quatro teoria elemento no qual o calor foi o mais leve dos quatro elementos. Muitos livros e artigos de ensino durante estes séculos apresentou estas teorias lado a lado. Da mesma forma, durante estes anos, o calor estava começando a ser distinguido em diferentes categorias de classificação, como "calor livre", "produção combinada de calor", "calor radiante", calor específico, capacidade de calor ", calor absoluta", "latente calórica", "livre" ou "perceptível" calórica (calorique sensível), entre outros.
Em 1780, por exemplo, Laplace e Lavoisier declarou: "Em geral, pode-se alterar a primeira hipótese para o segundo mudando as palavras" calor livre, produção combinada de calor e calor libertado 'em' . força viva, perda de força viva, e aumento da força viva '"Deste modo, a massa total de calorias num corpo, designado por calor absoluto, foi considerado como uma mistura de dois componentes; o calórica livre ou perceptível poderia afetar um termômetro enquanto o outro componente, o calórica latente, não podia. O uso das palavras "calor latente" implicava uma semelhança com o calor latente no sentido mais usual; foi considerado como quimicamente ligados às moléculas do corpo. No adiabatic compressão de um gás do calor absoluto permaneceu constante com o aumento observado da temperatura, o que indica que alguns calórica latente tinha-se tornado "livre" ou perceptível.
Durante o início do século 19, o conceito de calórico perceptível ou livre começou a ser referido como "calor livre" ou calor libertado. Em 1824, por exemplo, o físico francês Sadi Carnot, em suas famosas "Reflexões sobre o Motive Power of Fire", fala de quantidades de calor 'absorvido ou libertado' em transformações diferentes. Em 1882, o físico e fisiologista alemão Hermann von Helmholtz cunhou a expressão "energia livre" para a expressão E - TS, em que a mudança no F (ou G) determina a quantidade de energia "livre" para trabalhar nas condições dadas.
Assim, em utilização tradicional, o termo "livre" foi ligada a energia livre de Gibbs, ou seja, para os sistemas a uma pressão e temperatura constante, ou a energia livre de Helmholtz, ou seja, para os sistemas em volume e temperatura constante, para significar 'disponível sob a forma de trabalho útil. ' Com referência à energia livre de Gibbs, nós adicionamos a qualificação que é a energia livre para o trabalho não-volume.
Um número crescente de livros e artigos de revistas não incluir o anexo "livre", referindo-se a G como simplesmente Gibbs energia (e também para o Energia Helmholtz). Este é o resultado de um 1988 IUPAC reunião para definir terminologias unificadas para a comunidade científica internacional, em que o adjetivo "livre" supostamente foi banido. Esta norma, no entanto, ainda não foi adotado universalmente, e muitos artigos e livros publicados ainda incluir o descritivo "livre".
Energia livre de reações
Para derivar a equação da energia livre de Gibbs para um sistema isolado, deixe-S tot ser a entropia total do sistema isolado, isto é, um sistema que não pode trocar calor ou massa com o seu entorno. De acordo com a segunda lei da termodinâmica :
e se 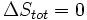 em seguida, o processo é reversível. A transferência de calor
em seguida, o processo é reversível. A transferência de calor 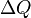 desaparece para um sistema adiabático. Qualquer processo adiabático que também é reversível é chamado um isentropic
desaparece para um sistema adiabático. Qualquer processo adiabático que também é reversível é chamado um isentropic 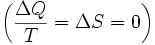 processo.
processo.
Agora considere sistemas diabático, tendo interna entropia S int. Um tal sistema é ligado termicamente ao seu ambiente, que têm a entropia S ext. O formulário de entropia da segunda lei não se aplica diretamente para o sistema diabático, ele só se aplica ao sistema fechado formado por tanto o sistema e seus arredores. Portanto, um processo é possível se
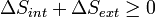 .
.
Vamos tentar expressar o lado esquerdo desta equação inteiramente em termos de funções de estado Ds ext é definido como.:
A temperatura T é a mesma para dois sistemas em equilíbrio térmico. Pelo lei zero da termodinâmica, se um sistema está em equilíbrio térmico com um segundo e um terceiro sistema, os dois últimos estão em equilíbrio bem. Além disso, 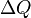 calor é transferido para o sistema, de modo
calor é transferido para o sistema, de modo 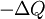 é o calor transferido para o ambiente, e -ΔQ / T é entropia adquirida pelos arredores. Temos agora:
é o calor transferido para o ambiente, e -ΔQ / T é entropia adquirida pelos arredores. Temos agora:
Multiplique ambos os lados por T:
ΔQ calor é transferido para o sistema; Se o processo é agora assumida como sendo isobaric, em seguida, ΔQ p = AH:
AHV é a variação de entalpia de reacção (por uma reacção química a pressão constante e temperatura). Em seguida
para um possível processo. Deixe a mudança Δ G na energia livre de Gibbs ser definido como
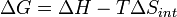 (Eq.1)
(Eq.1)
Note que ele não é definido em termos de quaisquer funções do Estado externos, como Δ S ext ou Δ S tot. Em seguida, a segunda lei torna-se, o que também nos diz sobre a espontaneidade da reação:
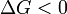 reação favorecida (espontânea)
reação favorecida (espontânea) 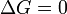 Nem a frente nem a reação inversa prevalece ( Equilibrium )
Nem a frente nem a reação inversa prevalece ( Equilibrium ) 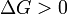 reação disfavored (não espontâneos)
reação disfavored (não espontâneos)
Gibbs energia livre G em si é definido como
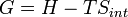 (Eq.2)
(Eq.2)
de notar que, para obter a equação (2) a partir da equação (1) devemos supor que T é constante. Assim, Gibbs energia livre é mais útil para processos termoquímicos a temperatura constante e pressão: tanto isotérmica e isobárica. Tais processos não se movem um em P - T diagrama, como a mudança de fase de uma substância pura, que tem lugar a uma pressão e temperatura de saturação. As reacções químicas, no entanto, não sofrem mudanças nas potencial químico, que é uma função de estado. Assim, os processos termodinâmicos não se limitam ao bidimensional P - diagrama V. Há uma terceira dimensão para n, a quantidade de gás. Naturalmente, para o estudo de explosivos químicos, os processos não são necessariamente isotérmica e isobárica. Para estes estudos, Energia livre de Helmholtz é usado.
Se um sistema fechado (Δ Q = 0) é a pressão constante (Δ Q = Δ H), seguida
Por conseguinte, a energia livre de Gibbs de um sistema fechado é:
e se 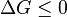 em seguida, o que implica que
em seguida, o que implica que 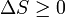 , De volta para onde nós começamos a derivação de Δ G.
, De volta para onde nós começamos a derivação de Δ G.
Identidades úteis
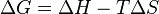 para temperatura constante
para temperatura constante 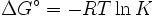
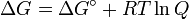
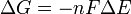
e rearranjando dá
que relaciona a um potencial eléctrico de reacção para o coeficiente de equilíbrio para que reacção.
onde
Δ G = mudança na energia livre de Gibbs, Δ H = mudança de entalpia , T = absoluto de temperatura , Δ S = mudança na entropia , R = constante do gás, ln = logaritmo natural , K = constante de equilíbrio, Q = quociente reacção, n = número de electrões por produto toupeira, F = Constante de Faraday ( coulombs por mole), e E = Δ potencial eléctrico da reacção. Além disso, temos também:
que relaciona a constante com energia livre de Gibbs equilíbrio.
Mudança padrão de formação
A energia livre de Gibbs padrão de formação de um composto é a variação de energia livre de Gibbs que acompanha a formação de 1 mole de essa substância a partir dos seus elementos componentes, na sua estados padrão (a forma mais estável do elemento a 25 graus Celsius e 100 kilopascals). Seu símbolo é Δ G f O.
Todos os elementos em seus estados padrão ( oxigênio , gás grafite, etc.) têm 0 standard Gibbs livre mudança da energia de formação, como não há nenhuma mudança envolvido.
- Δ G = Δ G ˚ + RT ln Q
Em equilíbrio, Δ G = 0 e Q = K modo que a equação torna-se Δ ˚ L = - RT ln K
Tabela de Substâncias Selecionadas
| Substância | Estado | Δ G ˚ ( cal / mol) |
|---|---|---|
| NH3 | g | -3,976 |
| H2O | LQ | -56,69 |
| H2O | g | -54,64 |
| CO2 | g | -94,26 |
| CO | g | -32,81 |
| CH 4 | g | -12,14 |
| C 2 H 6 | g | -7,86 |
| C 3 H 8 | g | -5,614 |
| C 8 H 18 | g | 4.14 |
| C 10 H 22 | g | 8.23 |