
La teoría de nudos
Antecedentes de las escuelas de Wikipedia
Esta selección Wikipedia está disponible sin conexión de SOS Children para su distribución en el mundo en desarrollo. Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/


La teoría de nudos es la matemática rama de topografía que los estudios nudos matemáticos, que se definen como embeddings de un círculo en 3 dimensiones espacio euclidiano , R 3. Esto es básicamente equivalente a una convencional cuerda anudada con los extremos se unieron para evitar que se convierta deshecho. Dos nudos matemáticos son equivalentes si uno puede ser transformado en el otro a través de una deformación de R 3 sobre sí misma (conocido como isotopía ambiente); estas transformaciones corresponden a las manipulaciones de una cuerda anudada que no implican el corte de la cadena o pasando la cuerda por sí mismo.
Los nudos pueden ser descritos en diversas decisiones. Teniendo en cuenta un método de la razón, sin embargo, puede haber más de una descripción que representa el mismo nudo. Por ejemplo, un método común de describir un nudo es un diagrama planar. Pero cualquier nudo dado se puede dibujar en muchas formas diferentes utilizando un diagrama planar. Por lo tanto, un problema fundamental en la teoría de nudos es determinar cuándo dos descripciones representan el mismo nudo. Una forma de nudos distintivas es mediante el uso de una nudo invariante, una "cantidad", que sigue siendo el mismo, incluso con diferentes descripciones de un nudo.
El concepto de un nudo se ha extendido a dimensiones más altas teniendo en cuenta n esferas dimensionales en m-dimensional espacio euclidiano. Esto fue investigado más activamente en el período 1960-1980, cuando se realizaron una serie de avances. En los últimos años, fenómenos de baja dimensionalidad han ganado el mayor interés.
La investigación en la teoría de nudos comenzó con la creación de tablas de nudo y la tabulación sistemática de nudos. Mientras tabulación sigue siendo una tarea importante, los investigadores de hoy tienen una amplia variedad de orígenes y objetivos. La teoría de nudos clásica, como iniciado por Max Dehn, JW Alexander, y otros, se refiere principalmente a la grupo nudo y invariantes de teoría de la homología, como la Polinomio de Alexander.
El descubrimiento de la Polinomio de Jones por Vaughan Jones en 1984, y las aportaciones posteriores de Edward Witten, Maxim Kontsevich, y otros, revelaron profundas conexiones entre la teoría de nudos y los métodos matemáticos en la mecánica estadística y la teoría cuántica de campos . Una plétora de invariantes de nudos se han inventado desde entonces, utilizando herramientas sofisticadas como grupos cuánticos y Homología Floer.
En los últimos 30 años, la teoría de nudos también se ha convertido en una herramienta en matemáticas aplicadas. Los químicos y los biólogos utilizan la teoría de nudos para entender, por ejemplo, quiralidad de las moléculas y las acciones de enzimas sobre ADN .
Historia
Nudos fueron estudiados por Carl Friedrich Gauss , quien desarrolló el Gauss que une integral para el cálculo de la vincular número de dos nudos. Su alumno Johann Benedict Listing, de quien Nudo de Listing es nombrado, promovido su estudio. El estímulo temprano, significativo en la teoría de nudos llegaría más tarde con Sir William Thomson (Lord Kelvin) y su teoría de los átomos de vórtice. (Sossinsky 2002, p. 1-3)

En 1867 después de observar escocés físico Los experimentos de Peter Tait involucran anillos de humo, Thomson llegó a la idea de que los átomos eran nudos de remolinos de vórtices en el Éter . Elementos químicos permitiría, pues, a los nudos y enlaces. Los experimentos de Tait se inspiraron en un documento de Helmholtz en vórtice tóricas en fluidos incompresibles. Thomson y Tait creían que la comprensión y clasificación de todos los nudos posibles explicarían por qué los átomos absorben y emiten luz en sólo la discreta longitudes de onda que lo hacen. Por ejemplo, Thomson pensó que el sodio podría ser el Hopf vincular debido a sus dos líneas de espectros. (Sossinsky 2002, p. 3-10)
Posteriormente Tait empezó a publicar nudos únicos en la creencia de que estaba creando una tabla de elementos. Formuló lo que ahora se conoce como el Tait conjetura sobre nudos alternos. (Las conjeturas se resolvieron finalmente en la década de 1990.) Tablas nudo de Tait se mejoraron posteriormente sobre por CN Little y TP Kirkman. (Sossinsky 2002, p. 6)
James Clerk Maxwell , un colega y amigo de Thomson y Tait de, también desarrolló un fuerte interés en nudos. Maxwell estudió la obra de Cotización en nudos. Él re-interpretado Gauss vinculación integral en términos de la teoría electromagnética. En su formulación, la integral representa el trabajo realizado por una partícula cargada que se mueve a lo largo de uno de los componentes del enlace bajo la influencia del campo magnético generado por una corriente eléctrica a lo largo del otro componente. Maxwell también continuó el estudio de los anillos de humo teniendo en cuenta tres anillos que interactúan.
Cuando no se detectó el éter luminoso en el Experimento de Michelson-Morley, teoría vórtice se convirtió en algo completamente obsoleto, y la teoría de nudos dejó de ser de gran interés científico. La física moderna demuestra que las longitudes de onda discretas dependen los niveles de energía cuántica.
Tras el desarrollo de la topología en el siglo 20 encabezada por Henri Poincaré, topologists como Max Dehn, JW Alexander, y Kurt Reidemeister, investigó nudos. Fuera de esto surgió la Reidemeister movimientos y la Alexander polinomio. (Sossinsky 2002, p. 15-45) Dehn también desarrolló Cirugía Dehn, que relaciona nudos a la teoría general de las 3-variedades, y formuló la Problemas de Dehn en la teoría de grupos , como el problema de la palabra. Los primeros pioneros en la primera mitad del siglo 20 incluyen Ralph Fox, quien popularizó el tema. En este primer período, la teoría de nudos se componía fundamentalmente de estudio en el grupo nudo y invariantes homológicas del complemento nudo.
Unos descubrimientos importantes en el siglo 20 revivieron en gran medida la teoría de nudos. La primera fue Teorema hiperbolización de Thurston que introdujo la teoría de hiperbólicas 3-variedades en la teoría de nudos y lo hicieron de gran importancia. El trabajo de Thurston también llevó, después de mucha expansión por otros, para el uso efectivo de las herramientas de teoría de la representación y geometría algebraica. Importantes resultados siguieron, incluyendo el Teorema Gordon-Luecke, que mostraron que los nudos se determinaron (hasta de reflexión especular) por sus complementos, y la Smith conjetura.
El interés en la teoría de los nudos de la comunidad matemática general creció significativamente después Descubrimiento Vaughan Jones 'de la Polinomio de Jones. Esto condujo a otros polinomios nudo tales como la polinomio de soporte, Polinomio HOMFLY, y Polinomio de Kauffman. Jones recibió el más alto honor en matemáticas, la Medalla Fields, en el año 1990 por este trabajo. (Sossinsky 2002, p. 71-89) En 1988 Edward Witten propone un nuevo marco para el polinomio de Jones, utilizando las ideas existentes desde la física matemática , tales como Integrales de trayectoria de Feynman, y la introducción de nuevos conceptos como teoría cuántica topológica campo (Witten 1989). Witten también recibió la medalla Fields, en 1990, en parte por este trabajo. Descripción de Witten del polinomio Jones implicaba invariantes relacionados para 3-variedades. Aproximaciones simultáneas, pero diferentes, por otros matemáticos dieron como resultado la Invariantes Witten-Reshetikhin-Turaev y varios de los llamados " invariantes cuánticos ", que parecen ser la versión matemáticamente rigurosa de los invariantes de Witten (Turaev 1994).
A principios de 1990, invariantes de nudos que abarcan el polinomio de Jones y sus generalizaciones, llamada invariantes tipo finitos, fueron descubiertos por Vassiliev y Goussarov. Estas invariantes, describieron inicialmente utilizando medios topológicas "clásicos", se mostraron por 1.994 campos Medallista Maxim Kontsevich que el resultado de la integración , mediante el Kontsevich integral, de ciertas estructuras algebraicas (Kontsevich 1993, Bar-Natan 1995).
Estos avances fueron seguidos por el descubrimiento de Khovanov homología y nudo Floer homología, que generalizar en gran medida los polinomios de Jones y Alexander. Estas teorías de homología han contribuido a una mayor integración de la perspectiva de la teoría de nudos.
En las últimas décadas del siglo 20, los científicos y matemáticos comenzaron a encontrar aplicaciones de la teoría de los nudos a los problemas de la biología y la química . La teoría de nudos puede ser usado para determinar si una molécula es quiral (tiene una "imparcialidad") o no. Los compuestos químicos de diferente uso de las manos pueden tener diferentes propiedades drásticamente, talidomida es un ejemplo notable de esto. Más en general, nudo métodos teóricos han sido utilizados en el estudio topoisomers, topológicamente diferentes disposiciones de la misma fórmula química. La teoría estrechamente relacionado de enredos se han usado eficazmente en el estudio de la acción de ciertas enzimas en el ADN. (Flapan 2000)
Equivalencia Nudo
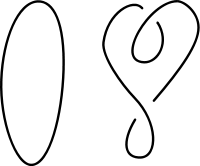
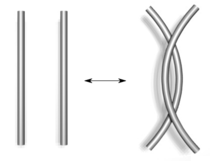
Un nudo se crea a partir de un uno segmento de línea dimensional, envolviéndolo alrededor de sí mismo de manera arbitraria y, a continuación la fusión de sus dos extremos libres entre sí para formar un bucle cerrado. Cuando topologists matemáticos consideran nudos y otros enredos como enlaces y trenzas, que describen cómo se posiciona el nudo en el espacio a su alrededor, llamado espacio ambiente. Si el nudo se puede mover sin problemas, sin cortar o pasar un segmento a través de otro, hasta que coincida con otro nudo, los dos nudos se consideran equivalentes. La idea de la equivalencia nudo es dar una definición precisa de cuando dos inmersiones deben ser considerados iguales.
El problema básico de la teoría de nudos, el problema de reconocimiento, por lo tanto se puede afirmar:. Dado dos nudos, determinar si son equivalentes o no Algoritmos existen para resolver este problema, con la primera dada por Wolfgang Haken. Sin embargo, estos algoritmos utilizan muchos pasos, y un tema importante en la teoría es comprender lo difícil este problema es en realidad (Hass 1997). El caso especial de reconocimiento de la unknot, llamado el unknotting problema, es de particular interés.
Diagramas Nudo
Una forma útil de visualizar y manipular nudos es proyectar el nudo sobre un plano-pensar el nudo proyectando una sombra en la pared. Una pequeña perturbación en la elección de la proyección se asegurará de que es uno a uno, excepto en los puntos dobles, llamadas cruces, donde la "sombra" del nudo se cruza una vez transversalmente (Rolfsen 1976). En cada cruce debemos indicar que la sección está "sobre" y que es "bajo", de manera que sea capaz de recrear el nudo inicial. Esto se suele hacer mediante la creación de una ruptura en la cadena que va por debajo.
Reidemeister mueve
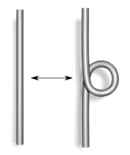
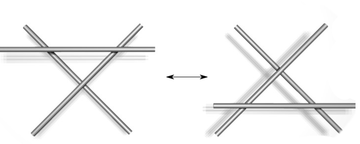
En 1927, trabajando con esta forma de diagrama de nudos, JW Alexander y GB Briggs, y de forma independiente Kurt Reidemeister, demostró que dos diagramas nudo pertenecientes a un mismo nudo pueden estar relacionados por una secuencia de tres tipos de movimientos en el diagrama, se muestran a continuación. Estas operaciones, que ahora se llaman los movimientos Reidemeister, son:
- Girar y desenroscar en cualquier dirección.
- Mover un capítulo completo sobre otra.
- Mover un capítulo completo sobre o debajo de un cruce.
 |  |
| Tipo I | Tipo II |
 | |
| Tipo III | |
Invariantes Nudo
Un invariante nudo es una "cantidad" que es el mismo para los nudos equivalentes (Adams 2001, Lickorish 1997, Rolfsen 1976). Un invariante puede tomar el mismo valor en dos nudos diferentes, por lo que por sí mismo puede ser incapaz de distinguir todos los nudos. Un invariante elemental es tricolorability.
"Clásicos" invariantes de nudos incluyen la grupo de nudo, que es el grupo fundamental de la complemento nudo, y el Alexander polinomio, que se puede calcular a partir de la invariante Alexander, un módulo construido a partir de la cubierta cíclico infinito del complemento nudo (Lickorish 1997, Rolfsen 1976). A finales del siglo 20, se descubrieron invariantes como "cuánticos" polinomios nudo e invariantes hiperbólicos. Estas invariantes mencionados son sólo la punta del iceberg de la teoría de nudos moderna.
Polinomios Nudo
Un polinomio nudo es una invariante nudo que es un polinomio . Ejemplos bien conocidos incluyen el Jones y Polinomios de Alexander. Una variante del polinomio Alexander, la Alexander-Conway polinomio, es un polinomio en la variable z con enteros coeficientes (Lickorish 1997).
Supongamos que se nos da un diagrama de enlace que está orientada, es decir, todos los componentes del enlace tiene una dirección preferida indicada por una flecha. Supongamos también 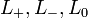 son diagramas de enlace orientados resultantes de cambiar el diagrama en un cruce especificada del diagrama, como se indica en la figura:
son diagramas de enlace orientados resultantes de cambiar el diagrama en un cruce especificada del diagrama, como se indica en la figura:
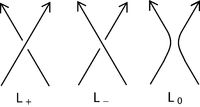
Entonces el polinomio de Alexander-Conway, C (z), se forma recursiva define de acuerdo con las reglas:
- C (O) = 1 (donde O es cualquier diagrama de la desanudar)
La segunda regla es lo que se refiere a menudo como un relación madeja. Para comprobar que estas reglas dan un invariante, se debe determinar que el polinomio no cambia bajo los tres movimientos Reidemeister. Muchos polinomios nudo importantes se pueden definir de esta manera.
El siguiente es un ejemplo de un cálculo típico que utiliza una relación madeja. Se calcula el polinomio de Alexander-Conway de la nudo de trébol. Las manchas amarillas indican el lugar donde se aplicó la relación.
- C (
 ) = C (
) = C (  ) + Z C (
) + Z C (  )
)
da la unknot y la Enlace Hopf. La aplicación de la relación con el enlace Hopf donde se indica,
- C (
 ) = C (
) = C (  ) + Z C (
) + Z C (  )
)
da un deformable enlace a uno con 0 cruces (en realidad es el desvincular de dos componentes) y un unknot. El desenlace toma un poco de sneakiness:
- C (
 ) = C (
) = C (  ) + Z C (
) + Z C (  )
)
lo que implica que C (desvincular de dos componentes) = 0, ya que los dos primeros polinomios son de la unknot y por lo tanto iguales.
Poniendo todo esto junto mostrará:
- C (trébol) = 1 + z (0 + z) = 1 + z 2
Desde el polinomio de Alexander-Conway es una invariante nudo, esto demuestra que la estructura de trébol no es equivalente a la unknot. Así que el trébol realmente está "anudado".
En realidad, hay dos nudos de trébol, llamado el derecho y tréboles zurdos, que son imágenes especulares entre sí (tener un esquema del trébol dada anteriormente y cambiar cada cruce a la otra manera de obtener la imagen en el espejo). Estos no son equivalentes entre sí! Esto fue demostrado por Max Dehn, antes de la invención de los polinomios del nudo, usando grupos de métodos teóricos (Dehn 1914). Pero el polinomio de Alexander-Conway de cada tipo de trébol será el mismo, como puede verse por pasar por el cálculo por encima de la imagen en el espejo. El polinomio de Jones puede, de hecho, distinguir entre los nudos de trébol izquierda y diestros (Lickorish 1997).
Invariantes hiperbólicos
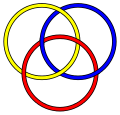
La Anillos de Borromeo son un vínculo con la propiedad de que la eliminación de un anillo desvincula los demás.
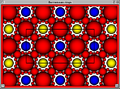
Ver cúspide de SnapPea: la Anillos de Borromeo complementan desde la perspectiva de un habitante de estar cerca de la componente rojo.
William Thurston demostró muchos nudos son nudos hiperbólicas, lo que significa que la complemento nudo, es decir, los puntos de 3-espacio no en el nudo, admitir una estructura geométrica, en particular la de geometría hiperbólica. La estructura hiperbólica depende sólo de la nudo por lo que cualquier cantidad calculada a partir de la estructura hiperbólica es entonces una invariante nudo. (Adams 2001)
Geometría nos permite visualizar lo que el interior de un nudo o enlace complemento parece imaginando los rayos de luz que viaja a lo largo de las geodésicas de la geometría. Un ejemplo es el de la imagen del complemento de la Anillos de Borromeo. El habitante de este enlace complemento está viendo el espacio de cerca el componente rojo. Las bolas en el cuadro son vistas horoball barrios del enlace. Espesando el enlace de una manera estándar, se obtiene lo que se llaman barrios horoball de los componentes del enlace. A pesar de que el límite de los barrios es un un toro, cuando se ve por dentro el complemento enlace, se ve como una esfera, llamada horoball. Cada componente de enlace se muestra como un número infinito de horoballs (de un color), ya que hay un número infinito de rayos de luz del observador en el componente de enlace. El paralelogramo fundamental (que se indica en la imagen), azulejos, tanto vertical como horizontalmente.
El patrón de horoballs es en sí una invariante útil. Otros invariantes hiperbólicos incluyen la forma de la paralleogram fundamental, longitud de geodésica más corto, y el volumen. Modernos esfuerzos nudo y enlace tabulación han utilizado con eficacia estas invariantes. Ordenadores rápidos y métodos inteligentes de la obtención de estos invariantes hacen el cálculo de estas invariantes, en la práctica, una tarea sencilla. (Adams, Hildebrand, y Weeks, 1991)
Dimensiones superiores
En cuatro dimensiones, cualquier bucle cerrado de cadena unidimensional es equivalente a un unknot. Podemos lograr la deformación necesaria en dos pasos. El primer paso es para "empujar" el bucle en un subespacio tridimensional, que siempre es posible, aunque técnica de explicar. El segundo paso está cambiando los cruces. Supongamos que una hebra está detrás de otro como se ve desde el punto elegido. Levante en la cuarta dimensión, por lo que no hay ningún obstáculo (la hebra delantera que no tiene componente allí); a continuación, deslice hacia adelante, y colocar de nuevo, ahora en el frente. Una analogía para el avión sería levantar una cadena arriba de la superficie.
Dado que un nudo se puede considerar topológicamente una esfera 1-dimensional, la siguiente generalización es considerar una esfera de dos dimensiones incrustado en una esfera de cuatro dimensiones. Dicha incorporación se desató si existe un homeomorfismo del 4-esfera sobre sí mismo tomando la 2-esfera a una "ronda" 2-esfera estándar. Nudos suspendidos y nudos hiladas son dos familias típicas de estos nudos 2-esfera.
La técnica matemática llamada "posición general" implica que para un dado n -sphere en el m -sphere, si m es lo suficientemente grande (en función de n), la esfera debe desató. En general, lineal a tramos esferas n- forman nudos sólo en (n 2) -espacio ( Christopher Zeeman 1963), aunque esto ya no es un requisito para esferas anudadas sin problemas. De hecho, hay problemas anudadas 4k-1 -spheres en -espacio 6k, por ejemplo, hay un sin problemas anudadas 3-esfera en el 6-esfera (Haefliger 1962, Levine 1965). Así, el codimension de un nudo suave puede ser arbitrariamente grande cuando no se fija la dimensión de la esfera de nudos; sin embargo, cualquier k -sphere suave en un -sphere n con 2n-3k-3> 0 se desató. La noción de un nudo tiene otras generalizaciones en matemáticas, consulte: nudo (matemáticas).
Adición de nudos
Dos nudos pueden añadir cortando ambos nudos y unirse a los pares de extremos. Esto puede ser formalmente definido de la siguiente manera (Adams 2001): considerar una proyección plana de cada nudo y suponen estas proyecciones son disjuntos. Encuentra un rectángulo en el plano en el que un par de lados opuestos tengan forma de arco a lo largo de cada nudo, mientras que el resto del rectángulo es disjunta de los nudos. Formar un nuevo nudo mediante la supresión de la primera pareja de lados opuestos y al lado del otro par de lados opuestos. El nudo resultante es la suma de los nudos originales.
Esta operación se denomina la suma nudo, o, a veces la suma conectado o composición de dos nudos. La suma nudo es conmutativa y asociativa . También hay una descomposición principal para un nudo que nos permite definir un nudo primo o compuesto, de forma análoga a primeros números y compuestas. El nudo de trébol es el más sencillo nudo principal. Nudos de dimensiones superiores se pueden añadir empalmando los n-esferas. Aunque no se puede formar el unknot en tres dimensiones mediante la adición de dos nudos no triviales, puede en dimensiones superiores, al menos si se considera nudos lisos en codimension al menos 3.
Nudos de tabulación
Tradicionalmente, los nudos se han catalogado en términos de cruzar número. El número de nudos no triviales de un número determinado de cruce aumenta rápidamente, haciendo tabulación computacionalmente difícil. Tablas nudo generalmente incluyen sólo los nudos principales y sólo una entrada para un nudo y su imagen especular (incluso si son diferentes). La secuencia del número de nudos primos de un número dado de cruce, hasta cruce número 16, es 0, 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2.176, 9.988, 46.972 , 253293, 1388705 ... (secuencia A002863 en OEIS ). Aunque se conocen límites superior e inferior exponenciales para esta secuencia, no se ha demostrado que esta secuencia es estrictamente creciente (Adams 2001).
Las primeras tablas de nudos por Tait, Little, y Kirkman utilizan diagramas de nudos, aunque Tait también utiliza un precursor de la Notación Dowker. Diferentes notaciones se han inventado para nudos que permiten la tabulación más eficiente.
Las tablas primeros intentaron una lista de todos los nudos de a lo sumo 10 cruces, y todos los nudos alternos de 11 cruces. El desarrollo de la teoría de nudos debido a Alexander, Reidemeister, Seifert, y otros facilitó la tarea de verificación y cuadros de nudos hasta e incluyendo 9 cruces fueron publicadas por Alexander-Briggs y Reidemeister a finales de 1920.
La primera verificación importante de este trabajo fue realizado en la década de 1960 por John Horton Conway, que no sólo desarrolló una nueva notación, sino también la Alexander-Conway polinomio (Conway 1970, Muñeca-Hoste 1991). Esto verifica la lista de los nudos de un máximo de 11 pasos y una nueva lista de enlaces de hasta 10 pasos. Conway encontró una serie de omisiones, pero sólo una duplicación en los Tait-Pequeñas mesas; sin embargo se perdió los duplicados llamados el Perko par, que sólo se notó en 1974 por Kenneth Perko (Perko 1974). Este famoso error se propagaría cuando Dale Rolfsen agrega una tabla nudo en su influyente texto, basado en la obra de Conway.
Notación Alexander-Briggs
Esta es la notación más tradicional, debido al papel 1927 de JW Alexander y G. Briggs y posteriormente ampliado por Dale Rolfsen en su tabla de nudo. La notación simplemente organiza nudos por su número de cruce. Uno escribe el número cruce con un subíndice para indicar su orden entre todos los nudos con ese número de cruce. Esta orden es arbitrario y por lo tanto no tiene ningún significado especial.
La notación Dowker
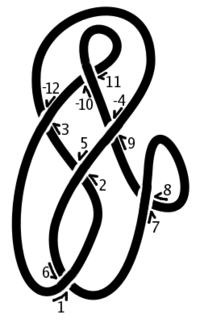
La notación Dowker, también llamada la notación Dowker-Thistlethwaite o código, por un nudo es una secuencia finita de enteros pares. Los números son generados siguiendo el nudo y el marcado de los cruces con enteros consecutivos. Desde cada cruce es visitado dos veces, esto crea un emparejamiento de enteros pares con números enteros impares. Un signo apropiado se da para indicar una y undercrossing. Por ejemplo, en la figura, el diagrama de nudo tiene cruces marcados con los pares (1,6) (3, -12) (5,2) (7,8) (9, -4) y (11, -10). La notación Dowker para este etiquetado es la secuencia: 6 -12 2 8 -4 -10. Un diagrama de nudo tiene más de una posible notación Dowker, y hay una ambigüedad bien entendido en la reconstrucción de un nudo de una notación Dowker.
Notación Conway
La notación Conway para nudos y enlaces, el nombre de John Horton Conway, se basa en la teoría de la ovillos (Conway 1970). La ventaja de esta notación es que refleja algunas propiedades del nudo o enlace.
La notación describe cómo construir un diagrama de enlace en particular del enlace. Comience con un poliedro básico, un 4-valente grafo plano conectado sin regiones Digon. Un poliedro Tal primero se denota por el número de vértices a continuación, un número de asteriscos que determinan la posición del poliedro en una lista de poliedro básico. Por ejemplo, 10 ** denota el segundo poliedro 10-vértice en la lista de Conway.
Cada vértice tiene entonces una maraña algebraica sustituido en ella (cada vértice está orientado para que no haya elección arbitraria en sustitución). Cada uno de esos enredos tiene una notación consistente en números y signos + o -.
Un ejemplo es 1 * 2 -3 2. El 1 * denota el único poliedro básico 1-vértice. El 2 -3 2 es una secuencia que describe la fracción continua asociada a un maraña racional. Una inserta esta maraña en el vértice del poliedro básico 1 *.
Un ejemplo más complicado es 8 * 3.1.2 0.1.1.1.1.1 aquí de nuevo 8 * se refiere a un poliedro básico con 8 vértices. Los períodos separan la notación para cada enredo.
Cualquier enlace admite tal descripción, y está claro que es una notación muy compacto, incluso para el número de cruce muy grande. Hay algunas abreviaturas más utilizadas habitualmente. El último ejemplo se escribe generalmente 8 * 3: 2 0, donde omitimos los queridos y mantuvimos el número de puntos con excepción de los puntos al final. Para un nudo algebraico como en el primer ejemplo, 1 * se omite con frecuencia.
Papel pionero de Conway sobre el tema muestra hasta 10 vértice poliedros básica de la que él usa para tabular enlaces, que se han convertido en estándar para esos vínculos. Para obtener una lista adicional de mayor poliedros vértice, hay opciones no estándar disponibles.

