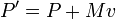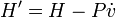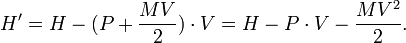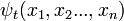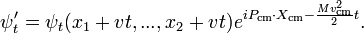Ecuación de Schrödinger
Antecedentes de las escuelas de Wikipedia
Esta selección wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selección Wikipedia para las escuelas. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/
| Mecanica cuantica |
|---|
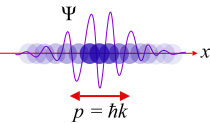 La dualidad onda-partícula |
| Introducción Glosario · Historia |
Fondo
|
Conceptos fundamentales
|
Experimentos
|
Formulaciones
|
Ecuaciones
|
Interpretaciones
|
Temas avanzados
|
|
Los científicos
|
En la física , especialmente la mecánica cuántica , la ecuación de Schrödinger es una ecuación que describe la forma en la estado cuántico de un sistema físico cambia en el tiempo. Es como elemento central de la mecánica cuántica que las leyes de Newton son de la mecánica clásica .
En la interpretación estándar de la mecánica cuántica, el estado cuántico, también llamado un vector función de onda o estado, es la descripción más completa que se puede dar a un sistema físico. Las soluciones a la ecuación de Schrödinger describen los sistemas atómicos y subatómicos, electrones y átomos, sino también los sistemas macroscópicos, posiblemente incluso el universo entero. La ecuación se nombra después Erwin Schrödinger, que lo descubrió en 1926.
La ecuación de Schrödinger puede ser matemáticamente transforma en Heisenberg de la mecánica de matrices, y en el Integral de caminos de Feynman. La ecuación de Schrödinger describe el tiempo de una manera que es inconveniente para las teorías relativistas, un problema que es menos severa en la formulación de Heisenberg y completamente ausente en la ruta de acceso integral.
La ecuación de Schrödinger
Hay varias ecuaciones de Schrödinger diferentes.
Sistema cuántico general
Para un sistema cuántico general:
donde
-
 es el función de onda, que es el amplitud de probabilidad para diferentes configuraciones.
es el función de onda, que es el amplitud de probabilidad para diferentes configuraciones.  es Sobre la constante de Planck
es Sobre la constante de Planck  , Y se puede ajustar a un valor de 1 cuando se usa unidades naturales.
, Y se puede ajustar a un valor de 1 cuando se usa unidades naturales.  es el Hamiltoniano operador.
es el Hamiltoniano operador.
Partícula individual en tres dimensiones
Para una sola partícula en tres dimensiones:
donde
 es la función de onda, que es la amplitud de la partícula tenga una posición dada en un momento dado.
es la función de onda, que es la amplitud de la partícula tenga una posición dada en un momento dado. 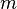 es la masa de la partícula.
es la masa de la partícula. 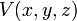 es la energía potencial de la partícula tiene en cada posición.
es la energía potencial de la partícula tiene en cada posición.
Antecedentes y el desarrollo histórico
Einstein interpretó Planck quanta 's como los fotones , partículas de luz, y propuso que la energía de un fotón es proporcional a su frecuencia, una misteriosa dualidad onda-partícula . Dado que la energía y el impulso son relacionadas de la misma manera como la frecuencia y número de onda en relatividad, se deducía que el impulso de un fotón es proporcional a su número de onda.
DeBroglie la hipótesis de que esto es cierto para todas las partículas, para los electrones, así como los fotones, que la energía y el momento de un electrón son la frecuencia y el número de onda de una onda. Suponiendo que las ondas viajan más o menos a lo largo de caminos clásicos, mostró que forman ondas estacionarias sólo para ciertas frecuencias discretas, los niveles de energía discretos que reproducen la viejo estado cuántico.
El seguimiento de estas ideas, Schrödinger decidió encontrar una ecuación de onda adecuada para el electrón. Él fue guiado por La analogía de Hamilton entre la mecánica y la óptica, codificado en la observación de que el límite de cero de longitud de onda de la óptica se asemeja a un sistema mecánico --- las trayectorias de los rayos de luz se convierten en pistas afilados que obedecen a una principio de mínima acción. Hamilton cree que la mecánica era el límite cero-longitud de onda de propagación de la onda, pero no formular una ecuación para esas ondas. Esto es lo que Schrödinger hizo, y una versión moderna de su razonamiento se reproduce en la siguiente sección. La ecuación que encontró es (en unidades naturales):
Usando esta ecuación, Schrödinger calcula la líneas espectrales de hidrógeno por tratamiento de un hidrógeno sola negativa del átomo cargado electrón como una onda, 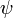 , Moviéndose en una pozo de potencial, V, creado por la carga positiva del protón . Este cálculo reproduce los niveles de energía de la Modelo de Bohr.
, Moviéndose en una pozo de potencial, V, creado por la carga positiva del protón . Este cálculo reproduce los niveles de energía de la Modelo de Bohr.
Pero esto no fue suficiente, ya que Sommerfeld ya había aparentemente reproduce correctamente correcciones relativistas. Schrödinger utiliza la relación impulso energía relativista para encontrar lo que hoy se conoce como el Ecuación de Klein-Gordon en un potencial de Coulomb :
Encontró a los parados ondas de esta ecuación relativista, pero las correcciones relativistas no estuvo de acuerdo con la fórmula de Sommerfeld. Desalentado, él guardó sus cálculos y se recluyó en una cabaña de montaña aislada con un amante.
Una vez allí, Schrödinger decidió que los cálculos no relativistas anteriores eran lo suficientemente novedoso para publicar, y decidió dejar fuera el problema de las correcciones relativistas para el futuro. Él formó su ecuación de onda y el análisis espectral de hidrógeno en un documento en 1926 .. El documento fue aprobado con entusiasmo por Einstein, que vio el asunto ondas como el antídoto visualizable a lo que él considera que es la excesivamente formal mecánica matricial.
La ecuación de Schrödinger le indica el comportamiento de  , Pero no dice lo que
, Pero no dice lo que  es. Schrödinger intentó sin éxito, en su cuarto trabajo, interpretarlo como una densidad de carga. En 1926 Max Born, tan sólo unos días después de la publicación de papel cuarta y última de Schrödinger, interpretado con éxito
es. Schrödinger intentó sin éxito, en su cuarto trabajo, interpretarlo como una densidad de carga. En 1926 Max Born, tan sólo unos días después de la publicación de papel cuarta y última de Schrödinger, interpretado con éxito  como una amplitud de probabilidad. Schrödinger, sin embargo, siempre se opuso a una estadística de aproximación o probabilística, con sus asociados discontinuidades; como Einstein, quien creía que la mecánica cuántica era una aproximación estadística a una teoría determinista subyacente, Schrödinger nunca se reconcilió con la Interpretación de Copenhague.
como una amplitud de probabilidad. Schrödinger, sin embargo, siempre se opuso a una estadística de aproximación o probabilística, con sus asociados discontinuidades; como Einstein, quien creía que la mecánica cuántica era una aproximación estadística a una teoría determinista subyacente, Schrödinger nunca se reconcilió con la Interpretación de Copenhague.
Derivación
Derivación heurístico Corto
Supuestos
- (1) El total de la energía E de una partícula es
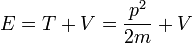
- Esta es la expresión clásica para una partícula con masa m donde la energía total E es la suma de la energía cinética ,
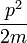 , Y la energía potencial V. El impulso de la partícula es p, o masa por velocidad. La energía potencial se supone varían con la posición, y, posiblemente, el tiempo también.
, Y la energía potencial V. El impulso de la partícula es p, o masa por velocidad. La energía potencial se supone varían con la posición, y, posiblemente, el tiempo también.
- Esta es la expresión clásica para una partícula con masa m donde la energía total E es la suma de la energía cinética ,
- Tenga en cuenta que la energía E y el impulso p aparecen en las siguientes dos relaciones:
- (2) Cuantos de luz hipótesis de Einstein de 1905, que afirma que la energía E de un fotón es proporcional a la frecuencia f de la onda electromagnética correspondiente:
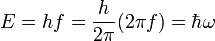
- donde el la frecuencia f de la cuantos de radiación (fotones) están relacionados por la constante h de Planck,
- y
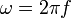 es el frecuencia angular de la onda.
es el frecuencia angular de la onda.
- (3) La hipótesis de Broglie de 1924, que establece que cualquier partícula puede estar asociada con una onda, representado matemáticamente por una función de onda Ψ, y que el impulso p de la partícula está relacionado con la longitud de onda λ de la onda asociada por:
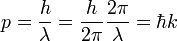
- donde
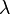 es el longitud de onda y
es el longitud de onda y 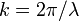 es el número de onda de la onda.
es el número de onda de la onda.
- donde
Expresando P y K como vectores , tenemos
Expresando la función de onda como onda plano complejo
La gran penetración de Schrödinger, a finales de 1925, era expresar la fase de una onda plana como un complejo factor de fase:
- donde
- y
y darse cuenta de que ya
entonces
y de manera similar desde:
entonces
y entonces:
de modo que, de nuevo por una onda plana, obtuvo:
Y mediante la inserción de estas expresiones para la energía y el momento en la fórmula clásica empezamos con obtenemos la ecuación de Schrödinger famosa para una sola partícula en el caso de 3 dimensiones en presencia de un potencial V:
La discusión más larga
La partícula se describe por una ola, y en unidades naturales, la la frecuencia es la energía E de la partícula, mientras que el impulso p es el número de onda k. No se trata de dos supuestos distintos, debido a la relatividad especial.
La energía total es la misma función de impulso y posición que en la mecánica clásica:
donde el primer término T (p) es la energía cinética y el segundo término V (x) es la energía potencial.
Schrödinger requiere que un Paquete de ondas en la posición x con número de onda k se moverá a lo largo de la trayectoria determinada por las leyes de Newton en el límite que la longitud de onda es pequeña.
Consideremos primero el caso sin un potencial, V = 0.
Para que una onda plana con la relación correcta de energía / frecuencia obedece a la ecuación de Schrodinger libre:
y sumando ondas planas, puede hacer una onda arbitraria.
Cuando no hay un potencial, un paquete de ondas debe viajar en línea recta a la velocidad clásica. La velocidad v de un paquete de ondas es:
que es el impulso en la masa como debe ser. Esta es una de Las ecuaciones de Hamilton de la mecánica:
después de identificar la energía y el impulso de un paquete de ondas como la frecuencia y el número de onda.
Para incluir una energía potencial, tenga en cuenta que a medida que una partícula se mueve la energía se conserva, por lo que para un paquete de ondas con aproximada número de onda k en la posición aproximada x la cantidad
debe ser constante. La frecuencia no cambia como una onda se mueve, pero el número de onda hace. Entonces, ¿dónde hay una energía potencial, se debe agregar la misma manera:
Esta es la ecuación de Schrödinger dependiente del tiempo. Es la ecuación de la energía en la mecánica clásica, se convirtió en una ecuación diferencial mediante la sustitución de:
Schrödinger estudió las soluciones de onda de pie, ya que estos eran los niveles de energía. Las ondas estacionarias tienen una dependencia complicada en el espacio, pero varían en el tiempo de una manera sencilla:
sustitución, la ecuación dependiente del tiempo se convierte en la ecuación de onda estacionaria:
¿Cuál es la ecuación original independiente del tiempo Schrodinger.
En un gradiente de potencial, el vector k de una onda de longitud de onda corta debe variar de punto a punto, para mantener constante la energía total. Hojas perpendicular al vector k son los frentes de onda, y cambian gradualmente dirección, porque la longitud de onda no es igual en todas partes. Un paquete de ondas sigue los frentes de onda de desplazamiento con la velocidad clásica, con la aceleración igual a la fuerza dividida por la masa.
una forma moderna fácil verificar que la segunda ley de Newton es válida para paquetes de ondas es tomar la Transformada de Fourier de la ecuación de Schrödinger dependiente del tiempo. Para un potencial polinomio arbitrario esto se llama la ecuación de Schrodinger en la representación de los impulsos:
La relación velocidad de grupo para la fourier trasformed paquete de ondas da la segunda de las ecuaciones de Hamilton.
Versiones
Hay varias ecuaciones que van por el nombre de Schrödinger:
Tiempo Ecuación Dependiente
Esta es la ecuación de movimiento para el estado cuántico. En la forma más general, está escrito:
Donde 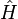 es un operador lineal actuando sobre la función de onda
es un operador lineal actuando sobre la función de onda  .
. 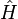 toma como una entrada
toma como una entrada  y produce otro de una manera lineal, una versión de función en el espacio de una matriz multiplicando un vector. Para el caso específico de una sola partícula en una dimensión en movimiento bajo la influencia de un potencial V:
y produce otro de una manera lineal, una versión de función en el espacio de una matriz multiplicando un vector. Para el caso específico de una sola partícula en una dimensión en movimiento bajo la influencia de un potencial V:
y el operador H se puede leer:
que es una combinación del operador que toma la segunda derivada, y el operador que multiplica pointwise  por V (x). Al dar curso
por V (x). Al dar curso  reproduce el lado derecho.
reproduce el lado derecho.
Para una partícula en tres dimensiones, la única diferencia es más derivados:
y para N partículas, la diferencia es que la función de onda se encuentra en el espacio de configuración 3N-dimensional, el espacio de todas las posibles posiciones de las partículas.
Esta última ecuación es en una dimensión muy alta, por lo que las soluciones no son fáciles de visualizar.
Tiempo Independiente Ecuación
Esta es la ecuación de las ondas estacionarias, el valor propio ecuación para H. En forma de resumen, para un sistema cuántico en general, está escrito:
Para una partícula en una dimensión, con la masa absorbida en reescalar el tiempo o el espacio:
Pero hay una restricción adicional --- la solución no debe crecer en el infinito, de manera que tiene una norma finita:
Por ejemplo, cuando no existe el potencial, la ecuación se lee:
que tiene soluciones oscilatorias para E> 0 (los de C son constantes arbitrarias):
y soluciones exponenciales para E <0
Las soluciones de crecimiento exponencial tienen una norma infinita, y no son física. No se les permite en un volumen finito con condiciones periódicas o fijos de contorno.
Para un potencial constante V la solución es oscilatoria para E> V y exponencial para E
Estados propios de energía
Una solución 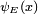 del tiempo ecuación independiente se llama un estado propio de energía con la energía E:
del tiempo ecuación independiente se llama un estado propio de energía con la energía E:
Para encontrar la dependencia temporal del Estado, considerar comenzar la ecuación tiempo-dependiente con una condición inicial 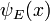 . La derivada en el tiempo t = 0 en todas partes es proporcional al valor de:
. La derivada en el tiempo t = 0 en todas partes es proporcional al valor de:
De modo que en toda la primera función sólo se reajustarán, y mantiene la propiedad de que su derivada en el tiempo es proporcional a sí mismo. Así que para todos los tiempos,
sustitución,
Así que la solución de la ecuación dependiente del tiempo con esta condición inicial es:
o, con explícita  s.
s.
Esta es una reafirmación de que las soluciones de la ecuación independiente del tiempo son las soluciones de onda estacionaria de la ecuación dependiente del tiempo. Sólo se multiplican por una fase con el tiempo, y de otra manera no se modifican.
Superposiciones de estados propios de energía cambian sus propiedades de acuerdo a las fases relativas entre los niveles de energía.
Propiedades
Primer Orden en el Tiempo
La ecuación de Schrödinger describe la evolución temporal de un estado cuántico, y debe determinar el valor futuro del valor actual. Una ecuación de campo clásica puede ser de segundo orden en derivados del tiempo, el estado clásico puede incluir la derivada temporal del campo. Pero un estado cuántico es una descripción completa de un sistema, de modo que la ecuación de Schrodinger es siempre de primer orden en el tiempo.
Lineal
La ecuación de Schrödinger es lineal en la función de onda: si 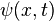 y
y 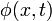 son soluciones de la ecuación dependiente del tiempo, entonces también lo es
son soluciones de la ecuación dependiente del tiempo, entonces también lo es 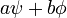 , Donde a y b son los números complejos .
, Donde a y b son los números complejos .
En la mecánica cuántica, la evolución temporal de un estado cuántico es siempre lineal, para razones fundamentales. Aunque hay versiones no lineales de la ecuación de Schrodinger, estas no son las ecuaciones que describen la evolución de un estado cuántico, pero las ecuaciones de campo clásicos como las ecuaciones de Maxwell o la Ecuación de Klein-Gordon.
La ecuación de Schrödinger en sí mismo puede ser pensado como la ecuación de movimiento para un campo clásico no para una función de onda, y teniendo este punto de vista, se describe una onda coherente de la materia no relativista, una ola de una Condensado de Bose o una superfluido con un gran número indefinido de partículas y una fase definida y amplitud.
Estados propios reales
La ecuación independiente del tiempo también es lineal, pero en este caso linealidad tiene un significado ligeramente distinto. Si dos funciones de onda 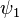 y
y 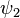 son soluciones de la ecuación independiente del tiempo con la misma energía E, entonces cualquier combinación lineal de los dos es una solución con energía E. Dos soluciones diferentes con la misma energía se llaman degenerada.
son soluciones de la ecuación independiente del tiempo con la misma energía E, entonces cualquier combinación lineal de los dos es una solución con energía E. Dos soluciones diferentes con la misma energía se llaman degenerada.
En un potencial arbitrario, hay una degeneración obvia: si una función de onda  resuelve la ecuación independiente del tiempo, también lo hace
resuelve la ecuación independiente del tiempo, también lo hace 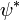 . Al tomar combinaciones lineales, la parte real e imaginaria de
. Al tomar combinaciones lineales, la parte real e imaginaria de  son cada uno soluciones. Así que la restricción de atención a funciones de onda valores reales no afecta el problema de valor propio independiente del tiempo.
son cada uno soluciones. Así que la restricción de atención a funciones de onda valores reales no afecta el problema de valor propio independiente del tiempo.
En la ecuación dependiente del tiempo, las ondas conjugadas complejas se mueven en direcciones opuestas. Dada una solución a la ecuación dependiente del tiempo 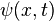 , La sustitución:
, La sustitución:
produce otra solución, y es la extensión del complejo de simetría conjugación con el caso dependiente del tiempo. La simetría de la conjugación compleja se llama inversión temporal.
Unitario Evolución Temporal
La ecuación de Schrodinger es unitario, lo que significa que la norma total de la función de onda, la suma de los cuadrados de valor en todos los puntos:
tiene derivada en el tiempo cero.
El derivado de 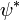 es de acuerdo a las ecuaciones conjugadas complejas
es de acuerdo a las ecuaciones conjugadas complejas
donde el operador 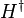 se define como la analógica continua de la Conjugado hermítica,
se define como la analógica continua de la Conjugado hermítica,
Para una base discreta, esto sólo significa que los elementos de matriz del operador obedecen lineal H:
El derivado del producto interno es:
y es proporcional a la parte imaginaria de H. Si H no tiene parte imaginaria, si es autoadjunto, entonces la probabilidad se conserva. Esto es cierto no sólo para la ecuación de Schrodinger como está escrito, pero para la ecuación de Schrodinger con salto no local:
tan largo como:
la elección particular:
reproduce el salto local en la ecuación de Schrodinger ordinaria. En una aproximación discreta de celosía a un espacio continuo, H (x, y) tiene una forma simple:
siempre que x e y son los vecinos más cercanos. En la diagonal
donde n es el número de vecinos más cercanos.
Energías Positivas
Las soluciones de la ecuación de Schrödinger en un potencial que está limitada a continuación tienen una frecuencia que está limitada a continuación. Para cualquier operador lineal 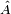 , El vector propio más pequeña minimiza la cantidad:
, El vector propio más pequeña minimiza la cantidad:
sobre todo  que son normalizada:
que son normalizada:
por el principio variacional.
El valor de la energía para la Schrodinger hamiltoniano es entonces el valor mínimo de:
después de una integración por partes, y el lado derecho es positivo cuando V es definida positiva.
Definida positiva Estado Ground no degenerado
Para potenciales que están delimitadas a continuación y no son infinitos sobre una región, hay un estado fundamental que minimiza la integral anterior. Esta función de onda menor energía es real y definida positiva.
Supongamos por contradicción que  es un estado de energía más bajo y tiene un cambio de signo, a continuación,
es un estado de energía más bajo y tiene un cambio de signo, a continuación, 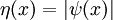 , El valor absoluto de
, El valor absoluto de  obedece
obedece
en todas partes, y
excepto para un conjunto de medida cero. Así 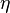 es también un minimimum de la integral, y tiene el mismo valor que
es también un minimimum de la integral, y tiene el mismo valor que  . Pero al suavizar las curvas en el cambio de signo, la contribución de degradado a la integral se reduce mientras que la energía potencial apenas se altera, por lo que la energía de
. Pero al suavizar las curvas en el cambio de signo, la contribución de degradado a la integral se reduce mientras que la energía potencial apenas se altera, por lo que la energía de 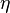 se puede reducir, lo cual es una contradicción.
se puede reducir, lo cual es una contradicción.
La falta de cambios de signo también demuestra que el estado fundamental es no degenerada, ya que si hubiera dos estados fundamentales con energía E que no eran proporcionales entre sí, una combinación lineal de los dos también sería un estado fundamental con un cero.
Estas propiedades permiten la continuación analítica de la ecuación Schrodinger a ser identificado como un proceso estocástico, que puede ser representado por un camino integral.
Lo completo
Los estados propios de energía constituyen una base --- cualquier función de onda se puede escribir como una suma sobre los estados discretos de energía o una integral sobre los estados de energía continuos, o más generalmente como una integral sobre una medida. Este es el teorema espectral en las matemáticas, y en un espacio de estados finitos es sólo una declaración de la integridad de los vectores propios de una matriz hermitiana.
Local de Conservación de la Probabilidad
La densidad de probabilidad de una partícula es 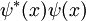 . El flujo de probabilidad se define como:
. El flujo de probabilidad se define como:
en unidades de (probabilidad) / (área x tiempo).
El flujo satisface la probabilidad ecuación de continuidad:
donde 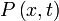 es el de densidad de probabilidad y se mide en unidades de (probabilidad) / (volumen) = r -3. Esta ecuación es el equivalente matemático de la probabilidad ley de conservación.
es el de densidad de probabilidad y se mide en unidades de (probabilidad) / (volumen) = r -3. Esta ecuación es el equivalente matemático de la probabilidad ley de conservación.
Para una onda plana:
Así que no sólo es la probabilidad de encontrar la partícula igual en todas partes, pero el flujo de probabilidad se como se espera de un objeto que se mueve a la velocidad clásica 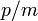 .
.
La razón de que la ecuación de Schrodinger admite un flujo de probabilidad se debe a que todo el salto es local y adelante en el tiempo.
Heisenberg Observables
Hay muchos operadores lineales que actúan sobre la función de onda, cada uno define una matriz de Heisenberg cuando los estados propios de energía son discretas. Para una sola partícula, el operador que toma la derivada de la función de onda en una cierta dirección:
Se llama el operador de momento. Multiplicando los operadores es igual que la multiplicación de matrices, el producto de A y B que actúa sobre  es una actuación en la salida del B actuando en
es una actuación en la salida del B actuando en  .
.
Un estado propio de p obedece a la ecuación:
para un número k, y por una función de onda normalizable esto restringe k para ser real, y el estado propio impulso es una onda con la frecuencia k.
El operador posición x multiplica cada valor de la función de onda en la posición x de x:
Así que para ser un estado propio de x, una función de onda debe concentrarse enteramente en un punto:
En términos de p, el hamiltoniano es:
Es fácil verificar que p que actúa sobre x que actúa sobre psi:
mientras que x actuando en p que actúa sobre psi reproduce sólo el primer término:
de manera que la diferencia de los dos no es igual a cero:
o en términos de los operadores:
ya que la derivada temporal de un estado es:
mientras que el complejo conjugado es
La derivada en el tiempo de un elemento de matriz
obedece a la ecuación de movimiento de Heisenberg. Esto establece la equivalencia de los formalismos Schrodinger y Heisenberg, ignorando los puntos finos matemáticos del procedimiento de limitación de espacio continuo.
Principio de correspondencia
La ecuación de Schrödinger satisface la principio de correspondencia. En el límite de los pequeños paquetes de ondas de longitud de onda, que reproduce las leyes de Newton. Esto es fácil de ver en la equivalencia con la mecánica de matrices.
Todos los operadores de formalismo de Heisenberg obedecen el análogo cuántico de las ecuaciones de Hamilton:
Así que, en particular, las ecuaciones de movimiento para los operadores X y P son:
en el Foto Schrodinger, la interpretación de esta ecuación es que da la velocidad de variación del elemento de matriz entre dos estados cuando los estados cambian con el tiempo. Tomando el valor esperado en cualquier estado muestra que las leyes de Newton no sólo tienen, en promedio, pero exactamente, para las cantidades:
Relatividad
La ecuación de Schrödinger no tiene en cuenta los relativistas efectos, como una ecuación de onda, es invariante bajo una Transformación de Galileo, pero no bajo una Transformación de Lorentz. Pero con el fin de incluir la relatividad, la imagen física debe ser alterado de manera radical.
Una generalización ingenua de la ecuación de Schrodinger utiliza la relación masa-energía relativista (en unidades naturales):
para producir la ecuación diferencial:
que es invariante relativista, pero de segundo orden en  , Por lo que no puede ser una ecuación para el estado cuántico. Esta ecuación también tiene la propiedad de que hay soluciones tanto con frecuencia positiva y negativa, una solución onda plana obedece:
, Por lo que no puede ser una ecuación para el estado cuántico. Esta ecuación también tiene la propiedad de que hay soluciones tanto con frecuencia positiva y negativa, una solución onda plana obedece:
que tiene dos soluciones, una con frecuencia positiva y el otro con frecuencia negativa. Esto es un desastre para la mecánica cuántica, porque significa que la energía no está acotado a continuación.
Un intento más sofisticado para solucionar este problema utiliza una ecuación de onda primera orden, el Ecuación de Dirac, pero de nuevo no son soluciones de energía negativa. Para solucionar este problema, es esencial para ir a una imagen multiparticle, y considerar las ecuaciones de onda como ecuaciones de movimiento para un campo cuántico, no para una función de onda.
La razón es que la relatividad es incompatible con una sola imagen de partícula. Una partícula relativista no puede ser localizada a una pequeña región sin el número de partículas convertirse en indefinido. Cuando una partícula se localiza en una caja de longitud L, el impulso es incierto por una cantidad más o menos proporcional a h / L por el principio de incertidumbre. Esto conduce a una incertidumbre de energía de hc / L, cuando | P | es lo suficientemente grande para que la masa de la partícula se puede despreciar. Esta incertidumbre en la energía es igual a la masa-energía de la partícula cuando
y esto se llama la Longitud de onda de Compton. Por debajo de esta longitud, es imposible para localizar una partícula y estar seguro de que se mantiene una sola partícula, ya que la incertidumbre de energía es lo suficientemente grande como para producir más partículas de la aspiradora por el mismo mecanismo que se localiza la partícula original.
Pero hay otro enfoque a la mecánica cuántica relativista, que no le permiten seguir trayectorias de las partículas individuales, y se descubrió dentro del -path integral formulación. Si las rutas de integración en la integral de camino incluyen rutas que se mueven hacia atrás y hacia delante en el tiempo como una función de su propio tiempo adecuado, es posible construir una función de onda de frecuencia puramente positiva para una partícula relativista. Esta construcción es atractivo, debido a que la ecuación de movimiento para la función de onda es exactamente la ecuación de onda relativista, pero con una restricción no local que separa las soluciones de frecuencia positivos y negativos. Las soluciones de frecuencia positivos viajan hacia adelante en el tiempo, las soluciones de frecuencia negativos viajan hacia atrás en el tiempo. De esta manera, ambos continúan analíticamente a una función de correlación ámbito estadístico, que también está representado por una suma sobre caminos. Pero en el espacio real, son las amplitudes de probabilidad para una partícula que viajar entre dos puntos, y se puede utilizar para generar la interacción de partículas en un punto de división y el marco de unión. El punto de partícula relativista de vista se debe a Richard Feynman.
El método de Feynman también construye la teoría de los campos cuantificados, pero desde un punto de vista de partículas. En esta teoría, las ecuaciones de movimiento para el campo se pueden interpretar como las ecuaciones de movimiento para una función de onda con precaución --- la función de onda sólo se define a nivel mundial, y de alguna manera relacionada con el momento adecuado de la partícula. La noción de una partícula localizada también es delicado --- una partícula localizada en la trayectoria de partícula relativista corresponde integrales al estado produce cuando un operador de campo local actúa en el vacío, y exacly qué estado se produce depende de la elección de las variables de campo.
Soluciones
Algunas técnicas generales son:
- Teoría de la perturbación
- La principio variacional
- Métodos Quantum Monte Carlo
- Teoría funcional de la densidad
- La Aproximación WKB y expansión semi-clásico
En algunos casos especiales, los métodos especiales pueden ser utilizados:
- Lista de los sistemas mecánicos cuánticos con soluciones analíticas
- Método de Hartree-Fock y métodos de post Hartree-Fock
- Delta-potencial Discrete método
Ecuación de Schrödinger gratuito
Cuando el potencial es cero, la ecuación de Schrödinger es lineal con coeficientes constantes:
donde  ha sido puesto a 1. La solución de
ha sido puesto a 1. La solución de 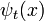 para cualquier condición inicial
para cualquier condición inicial 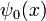 puede ser encontrada por Transformadas de Fourier. Debido a que los coeficientes son constantes, una ola inicial avión:
puede ser encontrada por Transformadas de Fourier. Debido a que los coeficientes son constantes, una ola inicial avión:
se mantiene una onda plana. Sólo los cambios coeficiente. Sustituyendo:
Así que A también está oscilando en el tiempo:
y la solución es:
Donde 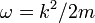 , Una reformulación de las relaciones de DeBroglie.
, Una reformulación de las relaciones de DeBroglie.
Para encontrar la solución general, escribir la condición inicial como una suma de ondas planas tomando su transformada de Fourier:
La ecuación es lineal, por lo que cada plano olas evoluciona de forma independiente:
¿Cuál es la solución general. Cuando se complementa con una método eficaz para la toma de Fourier transforma, se convierte en un algoritmo eficiente para encontrar la función de onda en cualquier momento futuro --- transformada de Fourier de las condiciones iniciales, se multiplica por una fase, y transformar de nuevo.
Gauss paquete de ondas
Un ejemplo sencillo e instructivo es el paquete de ondas gaussiano:
donde a es un número real positivo, el cuadrado de la anchura de la paquete de ondas. La normalización total de esta función de onda es:
La transformada de Fourier es una gaussiana de nuevo en términos de la número de onda k:
Con la convención de la física que pone los factores de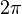 en transformadas de Fourier en el k-medida.
en transformadas de Fourier en el k-medida.
Cada onda separada única fase-gira en el tiempo, de modo que la solución de Fourier transformada dependiente del tiempo es:
La transformada inversa de Fourier sigue siendo una gaussiana, pero el parámetro se ha convertido en un complejo, y no es un factor global de normalización.
La rama de la raíz cuadrada es determinado por la continuidad en el tiempo --- es el valor que es más cercano a la raíz cuadrada positiva de un. Es conveniente cambiar la escala de tiempo para absorber m, reemplazando t / m por t.
La integral de  en todo el espacio es invariante, porque es el producto interno de
en todo el espacio es invariante, porque es el producto interno de  con el estado de energía cero, que es una onda con la longitud de onda infinita, una función constante del espacio. Para cualquier estado de energía, con la función de onda
con el estado de energía cero, que es una onda con la longitud de onda infinita, una función constante del espacio. Para cualquier estado de energía, con la función de onda 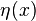 , el producto interior:
, el producto interior:
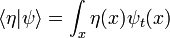 ,
,
sólo cambia en el tiempo de una manera simple: su fase gira con una frecuencia determinada por la energía de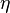 . Cuando
. Cuando 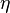 la energía tiene cero, como la onda de longitud de onda infinita, no cambia en absoluto.
la energía tiene cero, como la onda de longitud de onda infinita, no cambia en absoluto.
La suma de la plaza absoluta de  también es invariante, que es una declaración de la conservación de la probabilidad. Explícitamente en una dimensión:
también es invariante, que es una declaración de la conservación de la probabilidad. Explícitamente en una dimensión:
Que da la norma:
que ha conservado su valor, como debe ser.
La anchura de la gaussiana es la cantidad interesante, y se puede leer a partir de la forma de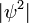 :
:
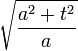 .
.
El ancho eventualmente crece linealmente en el tiempo, como se 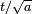 . trata de la difusión de ondas paquete --- no importa cómo reducir la función de onda inicial, una onda de Schrodinger, finalmente, se llena todo el espacio. El crecimiento lineal es un reflejo de la incertidumbre impulso --- el paquete de ondas se limita a una anchura estrecha
. trata de la difusión de ondas paquete --- no importa cómo reducir la función de onda inicial, una onda de Schrodinger, finalmente, se llena todo el espacio. El crecimiento lineal es un reflejo de la incertidumbre impulso --- el paquete de ondas se limita a una anchura estrecha 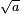 y por lo tanto tiene un impulso que es incierto por la cantidad recíproca
y por lo tanto tiene un impulso que es incierto por la cantidad recíproca 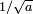 , un diferencial de velocidad de
, un diferencial de velocidad de 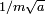 , y por lo tanto en la posición futura por
, y por lo tanto en la posición futura por 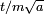 , donde el factor m ha sido restaurada por deshacer el cambio de escala antes de tiempo.
, donde el factor m ha sido restaurada por deshacer el cambio de escala antes de tiempo.
Invariancia galileana
Aumenta galileas son las transformaciones que se ven en el sistema desde el punto de vista de un observador que se mueve con una velocidad constante -v. Un impulso debe cambiar las propiedades físicas de un paquete de ondas en la misma forma que en la mecánica clásica:
Así que el factor de fase de una onda plana libre de Schrodinger:
sólo es diferente en las coordenadas impulsado por una fase que depende de x y t, pero no en p.
Una superposición arbitraria de soluciones de ondas planas con diferentes valores de p es la misma superposición de ondas planas impulsado, hasta un total de x, t factor de fase dependiente. Por lo que cualquier solución a la ecuación de Schrodinger libre, 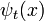 puede ser impulsado a otras soluciones:
puede ser impulsado a otras soluciones:
Impulsar una función de onda constante produce una onda plana. Más en general, impulsando una onda plana:
produce una onda impulsado:
Impulsar el paquete de ondas gaussiano difusión:
produce el movimiento de Gauss:
Que se propaga de la misma manera.
Propagador gratuito
El límite de poca anchura de la solución de paquete de ondas gaussiano es el propagador K. Para otras ecuaciones diferenciales, esto a veces se llama la función de Green, pero en la mecánica cuántica es tradicional reservar función el nombre de Green para el tiempo transformada de Fourier de K. Cuando a es la cantidad infinitesimal  , la condición inicial de Gauss, reescalado de manera que su integral es uno:
, la condición inicial de Gauss, reescalado de manera que su integral es uno:
se convierte en una función delta, por lo que su evolución en el tiempo:
da el propagador.
Tenga en cuenta que un paquete de ondas inicial muy estrecho se convierte al instante infinitamente ancho, con una fase que es más rápido oscilatorio en valores grandes de x. Esto puede parecer extraño --- la solución pasa de estar concentrada en un punto para estar en todas partes en todo momento más tarde, pero es un reflejo de la incertidumbre momento de una partícula localizada. También tenga en cuenta que la norma de la función de onda es infinito, pero esto también es correcto ya que el cuadrado de una función delta es divergente en la misma manera.
El factor de  es una cantidad infinitesimal, que está ahí para asegurarse de que las integrales sobre K están bien definidos. En el límite que
es una cantidad infinitesimal, que está ahí para asegurarse de que las integrales sobre K están bien definidos. En el límite que  se convierte en cero, K se convierte puramente oscilatorio y las integrales de K no son absolutamente convergente. En el resto de esta sección, se establece en cero, pero para que todas las integraciones más estados intermedios que estar bien definidos, el límite
se convierte en cero, K se convierte puramente oscilatorio y las integrales de K no son absolutamente convergente. En el resto de esta sección, se establece en cero, pero para que todas las integraciones más estados intermedios que estar bien definidos, el límite 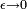 es sólo para ser tomada después se calcula el estado final.
es sólo para ser tomada después se calcula el estado final.
El propagador es la amplitud para alcanzar el punto x en el tiempo t, cuando se inicia en el origen, x = 0. Por la traducción de invariancia, la amplitud para llegar a un punto x al comenzar en el punto y es la misma función, solamente traducida:
En el límite cuando t es pequeño, el propagador converge a una función delta:
pero sólo en el sentido de las distribuciones. La integral de esta cantidad multiplicada por un diferenciable arbitraria función de prueba da el valor de la función de prueba en cero. Para ver esto, tenga en cuenta que la integral sobre todo el espacio de K es igual a 1 en todo momento:
ya que esta integral es el producto interno de K con la función de onda uniforme. Pero el factor de fase en el exponente tiene una derivada espacial distinto de cero en todas partes excepto en el origen, y así, cuando el tiempo es pequeño hay cancelaciones de fase rápida en todos menos un punto. Esto es rigurosamente cierto cuando el límite 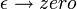 se toma después de todo lo demás.
se toma después de todo lo demás.
Así que el kernel de propagación es la evolución futura de tiempo de una función delta, y es continua en un sentido, converge a la función delta inicial en pequeños veces. Si la función de onda inicial es un pico infinitamente estrecha en la posición 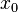 :
:
se convierte en la onda oscilatoria:
Debido a que cada función se puede escribir como una suma de picos estrechos:
la evolución temporal de cada función está determinada por el núcleo propagación:
Y esta es una forma alternativa de expresar la solución general. La interpretación de esta expresión es que la amplitud de una partícula que se encuentra en el punto x en el tiempo t es la amplitud que se inició a 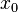 veces la amplitud que pasó de
veces la amplitud que pasó de 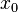 ax, sumada sobre todos los posibles puntos de partida. En otras palabras, se trata de una convolución de la K kernel con la condición inicial.
ax, sumada sobre todos los posibles puntos de partida. En otras palabras, se trata de una convolución de la K kernel con la condición inicial.
Como la amplitud de viajar de x a y después de un tiempo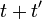 se puede considerar en dos pasos, el propagador obedece a la identidad:
se puede considerar en dos pasos, el propagador obedece a la identidad:
¿Qué se puede interpretar de la siguiente manera: la amplitud de viajar de x para z en el tiempo t + t 'es la suma de la amplitud de viajar de x a y en el tiempo t multiplicado por la amplitud de viajar desde y para z en el tiempo t' , sumada sobre todos los posibles estados intermedios y. Esta es una propiedad de un sistema cuántico arbitrario, y subdividiendo el tiempo en muchos segmentos, permite la evolución en el tiempo para ser expresado como una integral de camino.
Continuación analítica de Difusión
La difusión de paquetes de ondas en la mecánica cuántica está directamente relacionado con la difusión de densidades de probabilidad en difusión.Para una partícula que es caminar al azar, la función de densidad de probabilidad en cualquier punto satisface laecuación de difusión:
donde el factor de 2, que puede ser removido por un cambio de escala en tiempo o en el espacio, es sólo para conveniencia.
Una solución de esta ecuación es la propagación gaussiana:
y puesto que la integral de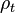 , es constante, mientras que la anchura se está convirtiendo en estrecha en pequeños veces, esta función se aproxima a una función delta en t = 0:
, es constante, mientras que la anchura se está convirtiendo en estrecha en pequeños veces, esta función se aproxima a una función delta en t = 0:
de nuevo, sólo en el sentido de las distribuciones, de modo que
para cualquier lisafunción de prueba f.
La propagación gaussiana es el núcleo de propagación para la ecuación de difusión y que obedece a laidentidad de convolución:
Que permite la difusión de expresarse como una integral de camino. El propagador es la exponencial de una H operador:
que es el operador de difusión infinitesimal.
Una matriz tiene dos índices, que en el espacio continuo hace que sea una función de x y x '. En este caso, a causa de traducción invariancia, el elemento de matriz K depende sólo de la diferencia de la posición, y un abuso de notación es conveniente para referirse al operador, los elementos de matriz, y la función de la diferencia por el mismo nombre:
Invariancia traducción significa que la multiplicación matriz continua:
es realmente convolución:
El exponencial puede definirse en un intervalo de t de que incluyen valores complejos, siempre y cuando integrales sobre la estancia kernel propagación convergente.
Mientras la parte real de z es positiva, para valores grandes de x K es exponencialmente decreciente y integrales sobre K son absolutamente convergente.
El límite de esta expresión para z acercándose al eje imaginario puro es el propagador Schrodinger:
y esto da una explicación más conceptual para la evolución en el tiempo de gaussianas. De la identidad fundamental de exponenciación, o la integración de ruta:
se cumple para todos los valores z complejas donde las integrales son absolutamente convergente para que los operadores están bien definidos.
Así que la evolución cuántica a partir de una gaussiana, que es el núcleo K de difusión:
da el estado de tiempo evolucionado:
Esto explica la forma de difusión de las soluciones de Gauss:
Principio variacional
La principio variacional afirma que para cualquier cualquier matriz hermitiana A, el valor propio más bajo minimiza la cantidad:
sobre la esfera unidad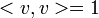 .Esto se sigue por el método delos multiplicadores de Lagrange, al mínimo el gradiente de la función es paralela a la pendiente de la restricción:
.Esto se sigue por el método delos multiplicadores de Lagrange, al mínimo el gradiente de la función es paralela a la pendiente de la restricción:
que es la condición autovalor
de manera que los valores extremos de una forma cuadrática A son los valores propios de A, y el valor de la función en los valores extremos es sólo el valor propio correspondiente:
Cuando la matriz hermitiana es el hamiltoniano, el valor mínimo es el nivel de energía más bajo.
En el espacio de todas las funciones de onda, la esfera unidad es el espacio de todas las funciones de onda normalizadas , los minimiza estado fundamental
, los minimiza estado fundamental
o, después de una integración por partes,
Todos los puntos estacionarios vienen en pares conjugados complejos ya que el integrando es real. Desde los puntos estacionarios son valores propios, cualquier combinación lineal es un punto estacionario, y la parte real e imaginaria son ambos puntos estacionarios.
El estado de energía más bajo tiene una función de onda definida positiva, porque da una  que minimiza la, integral
que minimiza la, integral 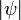 , el valor absoluto, es también un minimizador. Pero esta minimizador tiene esquinas agudas en los lugares donde
, el valor absoluto, es también un minimizador. Pero esta minimizador tiene esquinas agudas en los lugares donde  se registren cambios, y estas esquinas agudas puede redondearse a cabo para reducir la contribución de degradado.
se registren cambios, y estas esquinas agudas puede redondearse a cabo para reducir la contribución de degradado.
Potencial y Estado Ground
Para una partícula en un potencial definida positiva, la función de onda del estado fundamental que es real y positiva, y tiene una interpretación dual como la densidad de probabilidad para un proceso de difusión. La analogía entre la difusión y el movimiento cuántica no relativista, originalmente descubierto y explotado por Schrodinger, ha llevado a muchas soluciones exactas.
Una función de onda definida positiva:
es una solución a la ecuación de Schrödinger independiente del tiempo con m = 1 y el potencial:
con energía total cero. W, el logaritmo de la función de onda del estado fundamental. El segundo término derivado es de orden superior en  , e ignorando que da la aproximación semi-clásica.
, e ignorando que da la aproximación semi-clásica.
La forma de la función de onda del estado fundamental está motivada por la observación de que la función de onda del estado fundamental es la probabilidad de Boltzmann para un problema diferente, la probabilidad de encontrar una partícula de difusión en el espacio con la energía libre en diferentes puntos dados por W. Si la difusión obedece equilibrio detallado y la constante de difusión está en todas partes la misma, la ecuación de Fokker Planck de esta difusión es la ecuación de Schrodinger cuando se permite que el parámetro de tiempo para ser imaginario. Esta prolongación analítica da los estados propios una interpretación dual --- ya sea como los niveles de energía de un sistema cuántico, o los tiempos de relajación para una ecuación estocástica.
Oscilador armónico
Artículo principal: Oscilador armónico cuántico.
W debe crecer en el infinito, de modo que la función de onda tiene una integral finita. La forma más simple es analítica:
con una constante arbitraria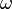 , lo que da el potencial:
, lo que da el potencial:
Este potencial se describe unoscilador armónico, con la función de onda del estado fundamental:
La energía total es cero, pero el potencial se desplaza por una constante. La energía del estado fundamental del unshifted potencial oscilador armónico habitual:
es entonces la constante de adición:
cuál es el energía de punto cero del oscilador.
Potencial de Coulomb
Otra forma simple pero útil es
donde W es proporcional a la coordenada radial. Este es el estado fundamental para dos potenciales diferentes, dependiendo de la dimensión. En una dimensión, el potencial correspondiente es singular en el origen, donde tiene algunos densidad diferente de cero:
y, hasta algún cambio de escala de las variables, este es el estado de energía más bajo para un potencial función delta, con la energía estado ligado añadido el.
con la energía del estado fundamental:
y la función de onda del estado fundamental:
En las dimensiones superiores, la misma forma da el potencial:
que se pueden identificar como la ley de Coulomb atractivo, hasta una constante aditiva que es la energía del estado fundamental. Este es el superpotencial que describe el nivel de energía más bajo del átomo de hidrógeno, una vez que la masa se restaura por análisis dimensional:
donde 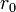 es el Radio de Bohr, con la energía
es el Radio de Bohr, con la energía
La ansatz
modifica el potencial de Coulomb para incluir un término cuadrático proporcional a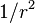 , que es útil para el momento angular distinto de cero.
, que es útil para el momento angular distinto de cero.
Formalismo Operador
Notación bra-ket
En el formulación matemática de la mecánica cuántica, un sistema físico está completamente descrito por un vector en un complejo espacio de Hilbert, la colección de todas las posibles funciones de onda normalizable. La función de onda es sólo un nombre alternativo para el vector de amplitudes complejas, y sólo en el caso de una sola partícula en la representación posición es que una ola en el sentido usual, una onda en el espacio tiempo. Para sistemas más complejos, es una onda en un enorme espacio de los mundos posibles. Dos vectores no nulos que son múltiplos de uno al otro, dos funciones de onda que son los mismos para cambiar la escala, representan el mismo estado físico.
El vector de función de onda se puede escribir de varias maneras:
- 1. como un resumenket vector:
- 2. Como una lista de los números complejos, los componentes en relación con una lista discreta de vectores de la base normalizable
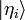 :
: - 3. Como una superposición continua de vectores de la base no normalizable, como los estados de posición
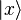 :
:
- 1. como un resumenket vector:
La brecha entre la base continua y la base discreta puede salvarse mediante la limitación de los argumentos. Los dos pueden ser unificados formalmente por el pensamiento de cada uno como medida en la línea número real.
En la notación más abstracto, la ecuación de Schrödinger está escrito:
que sólo dice que la función de onda evoluciona linealmente en el tiempo, y los nombres del operador lineal que da la derivada temporal del hamiltoniano H. En cuanto a la lista discreta de coeficientes:
que simplemente reafirma que la evolución el tiempo es lineal, ya que el hamiltoniano actúa por la multiplicación de matrices.
En una representación continua, el hamiltoniano es un operador lineal, que actúa por la versión continua de la multiplicación de matrices:
Tomando el conjugado complejo:
Para que el tiempo-evolución para ser unitario, para preservar los productos internos, la derivada en el tiempo del producto interior debe ser cero:
para un estado arbitrario 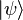 , lo que requiere que H es hermitiana. En una representación discreta esto significa que
, lo que requiere que H es hermitiana. En una representación discreta esto significa que 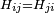 . cuando H es continua, debe ser autoadjunto, que añade algún requisito técnico que H no mezclar estados normalizable con los estados que violan las condiciones de frontera o que son extremadamente unnormalizable.
. cuando H es continua, debe ser autoadjunto, que añade algún requisito técnico que H no mezclar estados normalizable con los estados que violan las condiciones de frontera o que son extremadamente unnormalizable.
La solución formal de la ecuación es la matriz exponencial ( unidades naturales):
Por cada operador hamiltoniano independiente del tiempo,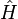 existe una serie de estados cuánticos,
existe una serie de estados cuánticos,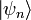 conocida comoestados propios de energía, y los correspondientes números reales
conocida comoestados propios de energía, y los correspondientes números reales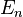 que satisfacen laecuación de valor propio.
que satisfacen laecuación de valor propio.
Esta es la ecuación de Schrödinger independiente del tiempo.
Para el caso de una sola partícula, el hamiltoniano es el operador lineal siguiente ( unidades naturales):
que es una operadores autoadjuntos cuando V no es demasiado singular y no crece demasiado rápido. Operadores autoadjuntos tienen la propiedad de que sus valores propios son reales, en cualquier forma, y sus vectores propios forman un conjunto completo, ya sea discreta o continua.
Expresado en una base de vectores propios de H, la ecuación de Schrodinger se vuelve trivial:
Lo que significa que cada estado propio energía sólo se multiplica por una fase compleja:
¿Qué es lo que significa la exponenciación matriz --- la evolución temporal actúa para girar las funciones propias de H.
Cuando H se expresa como una matriz para funciones de onda en una base de energía discreta:
de modo que:
Las propiedades físicas de los de C se extraen al actuar por operadores, matrices. Al redefinir la base de modo que gira con el tiempo, las matrices se vuelven dependientes de tiempo, que es la imagen Heisenberg.
Invariancia galileana
Simetría galileo requiere que H (p) es cuadrática en p tanto en el formalismo hamiltoniano clásica y cuántica. Para que aumenta galileanos para producir un factor de fase-p independiente píxeles - Ht deben tener una forma muy especial --- traducciones necesitadas p para ser compensados por un cambio en H. Esto sólo es cierto cuando H es cuadrática.
El generador infinitesimal de Aumenta tanto en el caso clásico y cuántico es:
donde la suma es sobre las diferentes partículas, y B, x, p son vectores.
El soporte de poisson / conmutador de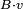 la x yp generar aumentos infinitesimales, con v el vector de velocidad impulso infinitesimal:
la x yp generar aumentos infinitesimales, con v el vector de velocidad impulso infinitesimal:
Iterando estas relaciones es simple, ya que añaden una cantidad constante en cada paso. Por iteración, del dv incrementalmente resumen de la cantidad finita V:
B dividida por la masa total es el centro actual de la posición de la masa menos las veces de tiempo el centro de velocidad de masa:
En otras palabras, B / M es la suposición actual de la posición de que el centro de masa tenía en el momento cero.
La afirmación de que B no cambia con el tiempo es el centro del teorema de masas. Para un sistema invariante de Galileo, el centro de masa se mueve con una velocidad constante, y la energía cinética total es la suma de la energía cinética centro de masa y la energía cinética medido con respecto al centro de la masa.
Puesto que B es explícitamente dependiente del tiempo, H no conmute con B, en lugar:
esto le da la ley de transformación para H bajo aumenta infinitesimales:
la interpretación de esta fórmula es que el cambio en H en virtud de un impulso infinitesimal está totalmente dada por el cambio del centro de la energía cinética de masa, que es el producto escalar de la cantidad de movimiento total con la velocidad de impulso infinitesimal.
Las dos cantidades (H, P) forman una representación de la galileo grupo con carga central M, donde sólo el H y P son funciones clásicas sobre los operadores de la mecánica cuántica espacio-fase o, mientras que M es un parámetro. La ley para la transformación infinitesimal v:
se pueden repetir como antes --- P va de P a P + MV en incrementos infinitesimales de v, mientras que H cambia en cada paso por una cantidad proporcional a P, que cambia linealmente. El valor final de H se cambia entonces por el valor de P a medio camino entre el valor inicial y el valor final:
Los factores proporcionales a la carga M central son las fases de la función de onda adicionales.
Aumenta dan demasiada información en el caso de una sola partícula, ya que la simetría galileo determina por completo el movimiento de una sola partícula. Dada una solución que depende del tiempo de múltiples partículas:
con un potencial que sólo depende de las posiciones relativas de las partículas, que puede ser utilizado para generar la solución impulsado:
Para el problema de onda estacionaria, el movimiento del centro de masa sólo añade una fase general. Cuando la solución de los niveles de energía de los sistemas multiparticle, invariancia galileana permite que el centro del movimiento de masas para ser ignorada.

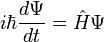
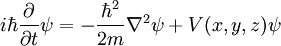
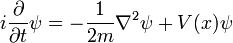
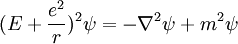
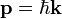
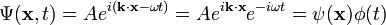
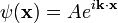
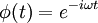
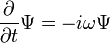
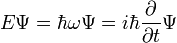
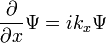
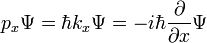
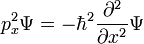
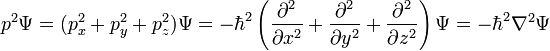
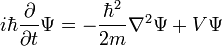

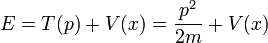
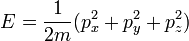
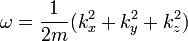
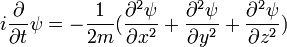
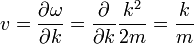
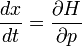
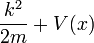
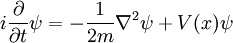
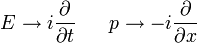
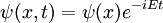
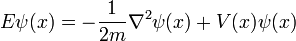
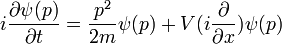
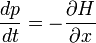
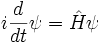
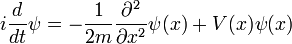
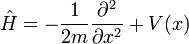
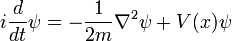
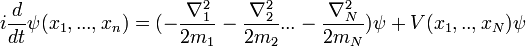
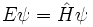
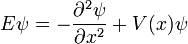
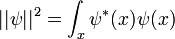
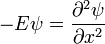
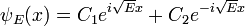
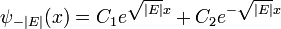
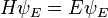
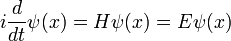
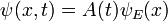
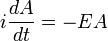
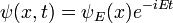
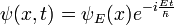
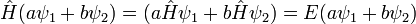
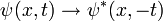
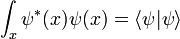
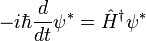
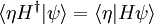
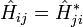

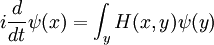
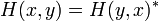
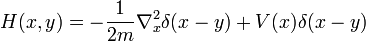
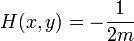
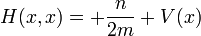
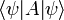
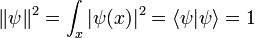
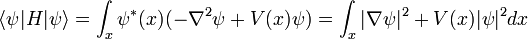
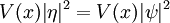
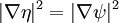
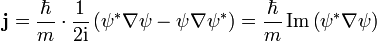
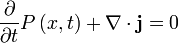
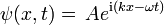
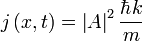
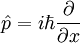
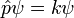
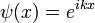
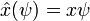
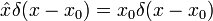
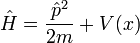
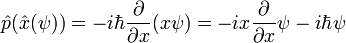
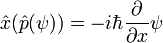
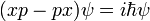
![[X, p] = xp - px = i \ hbar \,](../../images/532/53228.png)
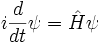
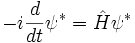
![{D \ over dt} \ langle \ eta | A | \ psi \ rangle = - \ eta \ hat HA \ psi + \ eta AH \ psi = [H, A] \,](../../images/532/53231.png)
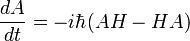
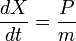
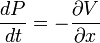
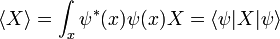
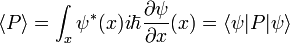
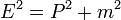
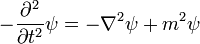
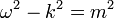
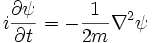
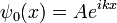
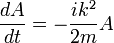
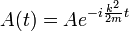
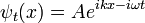
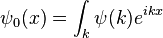
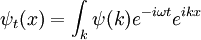
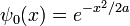
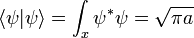
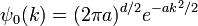
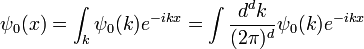
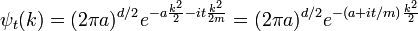
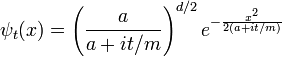
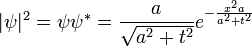
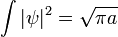
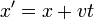
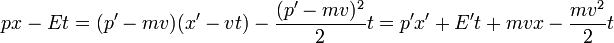
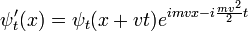
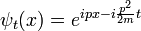
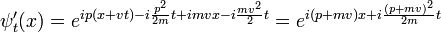
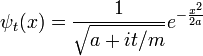
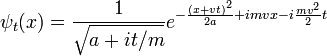
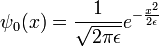
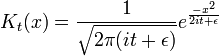
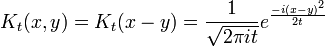
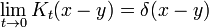
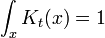
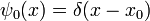
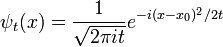
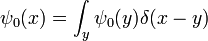
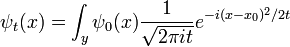
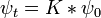
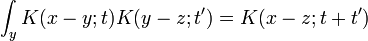
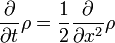
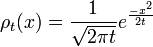
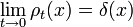
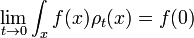
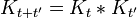
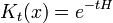
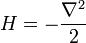
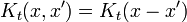
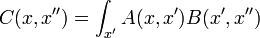
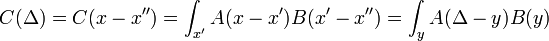
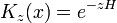
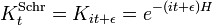
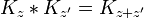
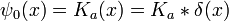
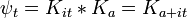
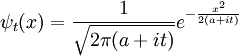
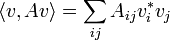
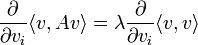
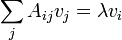
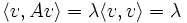
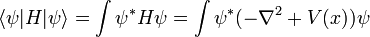
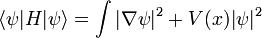
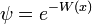
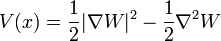
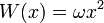
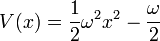
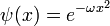
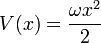
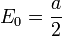
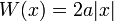
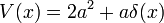
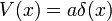
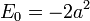
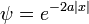
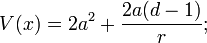
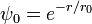
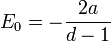
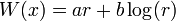
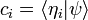
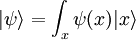
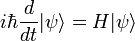
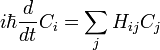
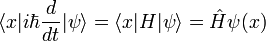
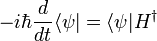
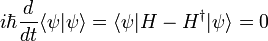
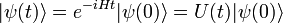
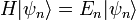
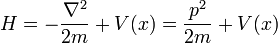
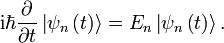
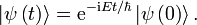
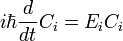
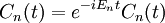
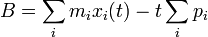
![[B\cdot v ,x_i] = vt
\,](../../images/533/53353.png)
![[B\cdot v ,p_i] = v m_i
\,](../../images/533/53354.png)
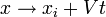
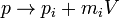
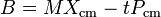
![{dB\over dt} = [H,B] + {\partial B \over \partial t} = 0
\,](../../images/533/53358.png)
![[B\cdot v,H] = - P_\mathrm{cm} v
\,](../../images/533/53359.png)