
Desacuerdo
Antecedentes de las escuelas de Wikipedia
Esta selección wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selección Wikipedia para las escuelas. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...
En teoría de la probabilidad y estadística , la varianza de una variable aleatoria , distribución de probabilidad , o la muestra es una medida de dispersión estadística, con un promedio del cuadrado de la distancia de sus posibles valores de la valor esperado (media). Considerando que la media es una manera de describir la localización de una distribución, la varianza es una manera de capturar su escala o grado de ser extendido. La unidad de varianza es el cuadrado de la unidad de la variable original. La raíz cuadrada de la varianza, llamada la desviación estándar , tiene las mismas unidades que la variable original y puede ser más fácil de interpretar por esta razón.
La varianza de una verdadera variable aleatoria -valued es su segundo momento central, y que también pasa a ser su segundo cumulante. Así como algunas distribuciones no tienen una media, algunos no tienen una varianza también. La media existe siempre que exista la varianza, pero no viceversa.
Definición
Si μ = E (X) es el valor esperado (media) de la variable aleatoria X, entonces la varianza es
Esta definición abarca las variables aleatorias que son discretos , continua , o ninguno. De todos los puntos sobre los cuales al cuadrado las desviaciones podrían haber sido calculados, la media produce el valor mínimo de la suma promedio de las desviaciones al cuadrado.
Muchas distribuciones, como la Distribución de Cauchy, no tienen una variación debido a las integral diverge pertinentes. En particular, si una distribución no tiene un valor esperado, no tiene una varianza tampoco. Lo contrario no es cierto: hay distribuciones para los que existe el valor esperado, pero la diferencia no.
Caso discreto
Si la variable aleatoria es discreta con función de masa de probabilidad p 1, ..., p n, esto es equivalente a
(Nota: esta variación se debe dividir por la suma de pesos en el caso de una discreta varianza ponderada). Es decir, es el valor esperado de la cuadrado de la desviación de X desde su propia media. En lenguaje llano, puede ser expresado como "El promedio del cuadrado de la distancia de cada punto de datos de la media". Por lo tanto, es la media desviación al cuadrado. La varianza de la variable aleatoria X es típicamente designado como Var (X), 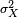 O, simplemente, σ 2.
O, simplemente, σ 2.
Propiedades
La varianza es no negativo, porque las plazas son positivos o cero. La varianza de una variable aleatoria es 0 si y sólo si la variable es degenerado, es decir, adquiere un valor constante con probabilidad 1, y la varianza de una variable en un conjunto de datos es 0 si y sólo si todas las entradas tienen el mismo valor.
La varianza es invariante con respecto a los cambios en un parámetro de localización. Es decir, si una constante se añade a todos los valores de la variable, la varianza es sin cambios. Si todos los valores son escalados por una constante, la varianza se escala por el cuadrado de esa constante. Estas dos propiedades se pueden expresar en la siguiente fórmula:
La varianza de una suma finita de variables aleatorias no correlacionadas es igual a la suma de sus varianzas.
- Supongamos que las observaciones se pueden dividir en subgrupos de acuerdo con algunos segundos variable. A continuación, la varianza del grupo total es igual a la media de las varianzas de los subgrupos más la varianza de las medias de los subgrupos. Esta propiedad se conoce como descomposición de la varianza o de la ley de la varianza total y desempeña un papel importante en el análisis de varianza. Por ejemplo, supongamos que un grupo está formado por un subgrupo de los hombres y una igualmente grande subgrupo de mujeres. Supongamos que los hombres tienen una longitud corporal medio de 180 y que la varianza de sus longitudes es de 100. Supongamos que las mujeres tienen una longitud media de 160 y que la varianza de sus longitudes es de 50. A continuación, la media de las varianzas es (100 + 50) / 2 = 75; la varianza de los medios es la varianza de 180, 160 que es de 100. A continuación, en el grupo total de hombres y mujeres combinados, la varianza de las longitudes de carrocería será 75 + 100 = 175. Tenga en cuenta que este usa N para el denominador en lugar de N - 1.
En un caso más general, si los subgrupos tienen tamaños desiguales, entonces deben ser ponderados en proporción a su tamaño en los cálculos de las medias y varianzas. La fórmula también es válido con más de dos grupos, e incluso si la variable de agrupación es continua.
Esta fórmula implica que la varianza del grupo total no puede ser menor que la media de las varianzas de los subgrupos. Tenga en cuenta, sin embargo, que la varianza total no es necesariamente más grande que las varianzas de los subgrupos. En el ejemplo anterior, cuando los subgrupos se analizan por separado, la varianza es influenciada sólo por las diferencias hombre-hombre y las diferencias mujer-mujer. Si se combinan los dos grupos, sin embargo, a continuación, los hombres-mujeres diferencias entran en la varianza también.
- Muchas fórmulas de cálculo para la varianza se basan en esta igualdad:. La varianza es igual a la media de los cuadrados menos el cuadrado de la media Por ejemplo, si tenemos en cuenta los números 1, 2, 3, 4 entonces la media de los cuadrados es (1 × 1 + 2 × 2 + 3 × 3 + 4 × 4) / 4 = 7.5. La media es 2,5, por lo que el cuadrado de la media es de 6,25. Por lo tanto la varianza es 07/05 a 06/25 = 1,25, que es de hecho el mismo resultado obtenido antes con las fórmulas definición. Muchas calculadoras de bolsillo utilizan un algoritmo que se basa en esta fórmula y que les permite calcular la varianza, mientras que los datos se introducen, sin almacenar todos los valores en la memoria. El algoritmo es ajustar sólo tres variables cuando se introduce un nuevo valor de los datos: El número de datos introducidos hasta el momento (n), la suma de los valores de la medida (S), y la suma de los valores al cuadrado hasta el momento (SS) . Por ejemplo, si los datos son de 1, 2, 3, 4, a continuación, después de introducir el primer valor, el algoritmo tendría que n = 1, S = 1 y SS = 1. Después de entrar en el segundo valor (2), habría n = 2, S = 3 y SS = 5. Una vez introducidos todos los datos, se tendrían que n = 4, S = 10 y SS = 30. A continuación, la media se calcula como M = S / n, y, finalmente, la varianza se calcula como SS / n - M × M. En este ejemplo, el resultado sería de 30/4 - 2,5 x 2,5 = 07/05 a 06/25 = 1,25. Si la estimación de la muestra es imparcial para ser calculados, el resultado será multiplicado por n / (n - 1), que produce 1.667 en este ejemplo.
Propiedades, formal
8.a. Varianza de la suma de variables no correlacionadas
Una de las razones para el uso de la varianza en preferencia a otras medidas de dispersión es que la varianza de la suma (o la diferencia) de variables aleatorias no correlacionadas es la suma de sus varianzas:
Esta afirmación se hace a menudo con la condición más fuerte que las variables son basta independientes, pero uncorrelatedness. Así que si las variables tienen la misma varianza σ 2, a continuación, ya que la división por n es una transformación lineal, esta fórmula inmediatamente implica que la varianza de su media es
Es decir, la varianza de la media disminuye con n. Este hecho se utiliza en la definición de la error estándar de la media de la muestra, que se utiliza en el teorema del límite central.
8.b. varianza de la suma de variables correlacionadas
En general, si las variables están correlacionadas, entonces la varianza de su suma es la suma de su covarianzas:
Aquí Cov es la covarianza, que es cero para las variables aleatorias independientes (si existe). La fórmula indica que la varianza de una suma es igual a la suma de todos los elementos de la matriz de covarianza de los componentes. Esta fórmula se utiliza en la teoría de El alfa de Cronbach en la teoría clásica de los tests.
Así que si las variables tienen igual varianza σ 2 y la correlación media de distintas variables es ρ, entonces la varianza de su media es
Esto implica que la varianza de la media aumenta con el promedio de las correlaciones. Por otra parte, si las variables tienen varianza unitaria, por ejemplo, si están estandarizados, entonces esto se simplifica a
Esta fórmula se utiliza en el Spearman-Brown fórmula de predicción de la teoría clásica de los tests. Esto converge a ρ si n tiende a infinito, a condición de que la correlación promedio se mantiene constante o converge también. Así que para la varianza de la media de las variables estandarizadas con correlaciones iguales o convergentes correlación promedio que tenemos
Por lo tanto, la varianza de la media de un gran número de variables estandarizadas es aproximadamente igual a su correlación promedio. Esto deja claro que la media de la muestra de variables correlacionadas no general no converge a la media de la población, a pesar de que la Ley de los grandes números establece que la media de la muestra convergerá para variables independientes.
8.c. varianza de una suma ponderada de las variables
Propiedades 6 y 8, además de esta propiedad de la La página de covarianza: Cov (aX, por) = ab Cov (X, Y) implica conjuntamente que
Esto implica que en una suma ponderada de las variables, la variable con el mayor peso tendrá un peso desproporcionadamente grande en la varianza del total. Por ejemplo, si X e Y no están correlacionados y el peso de X es dos veces el peso de Y, entonces el peso de la varianza de X será de cuatro veces el peso de la varianza de y.
9. La descomposición de la varianza
La fórmula general para descomposición de la varianza o de la ley de la varianza total es: Si X e Y son dos variables aleatorias y existe la varianza de X, entonces
Aquí, E (X | Y) es la expectativa condicional de X dado Y, y Var (X | Y) es la varianza condicional de X dado Y. (Una explicación más intuitiva es que dado un valor particular de Y, entonces X sigue una distribución con media E (X | Y) y la varianza Var (X |. Y) La fórmula anterior indica cómo encontrar Var (X) basado en el distribuciones de estas dos cantidades cuando se permite que Y para variar.) Esta fórmula se aplica a menudo en análisis de la varianza, donde la fórmula correspondiente es
También se utiliza en la regresión lineal análisis, donde la fórmula correspondiente es
Esto también se puede derivar de la aditividad de las varianzas (propiedad 8), ya que el (observado) puntuación total es la suma de la puntuación predicha y la puntuación de error, en donde los dos últimos son correlacionadas.
10. fórmula computacional para la varianza
La fórmula de cálculo para la varianza sigue de una manera directa de la linealidad de los valores esperados y la definición anterior:
Esto se utiliza a menudo para calcular la varianza en la práctica, aunque sufre de aproximación numérica error si las dos componentes de la ecuación son similares en magnitud.
Propiedad característica
El segundo momento de una variable aleatoria alcanza el valor mínimo cuando se toma alrededor de la media de la variable aleatoria, es decir, 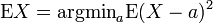 . Esta propiedad podría ser invertido, es decir, si la función
. Esta propiedad podría ser invertido, es decir, si la función 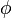 satisface
satisface 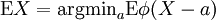 entonces es necesario de la forma
entonces es necesario de la forma 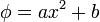 . Esto también es cierto en el caso multidimensional.
. Esto también es cierto en el caso multidimensional.
La aproximación de la varianza de una función
La método delta utiliza de segundo orden expansiones de Taylor a la aproximación de la varianza de una función de una o más variables aleatorios. Por ejemplo, la varianza aproximada de una función de una variable está dada por
a condición de que f es dos veces diferenciable y que la media y la varianza de X son finitos.
Las generalizaciones
Si 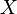 es un vector -valued variable aleatoria, con valores en
es un vector -valued variable aleatoria, con valores en 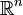 Y pensado como un vector columna, entonces la generalización natural de la varianza es
Y pensado como un vector columna, entonces la generalización natural de la varianza es 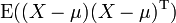 , Donde
, Donde 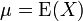 y
y  es la transpuesta de
es la transpuesta de  , Y por lo tanto es un vector fila. Esta variación es un matriz cuadrada semi-definida positiva, comúnmente conocida como la matriz de covarianza.
, Y por lo tanto es un vector fila. Esta variación es un matriz cuadrada semi-definida positiva, comúnmente conocida como la matriz de covarianza.
Si  es un complejo de variable aleatoria -valued, con valores en
es un complejo de variable aleatoria -valued, con valores en 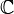 , A continuación, su varianza es
, A continuación, su varianza es 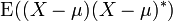 , Donde
, Donde 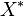 es el conjugado complejo de
es el conjugado complejo de 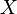 . Esta variación es también una matriz cuadrada semi-definida positiva.
. Esta variación es también una matriz cuadrada semi-definida positiva.
Historia
El término varianza se introdujo por primera vez por Ronald Fisher en su artículo de 1918 La correlación entre parientes en el supuesto de herencia mendeliana.
Momento de inercia
La varianza de una distribución de probabilidad es análoga a la momento de inercia en la mecánica clásica de una distribución correspondiente de masa a lo largo de una línea, con respecto a la rotación alrededor de su centro de masa. Es debido a esta analogía que cosas tales como la varianza se llaman momentos de las distribuciones de probabilidad . (La matriz de covarianza es análoga a la momento del tensor de inercia para distribuciones multivariantes.)

![\ Operatorname {var} (X) = \ operatorname {E} [(X - \ mu) ^ 2] \,.](../../images/82/8221.png)
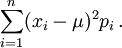
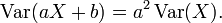
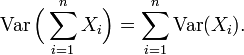
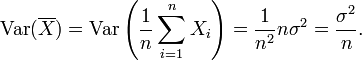
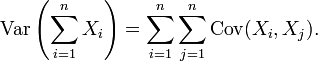
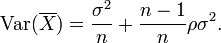
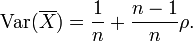
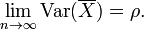
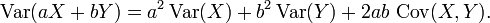
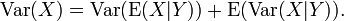
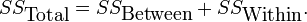
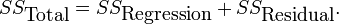
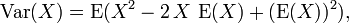
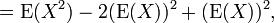
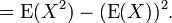
![\ Operatorname {var} \ left [f (X) \ right] \ aprox \ left (f '(\ operatorname {E} \ left [X \ right]) \ right) ^ 2 \ operatorname {var} \ left [X \ right]](../../images/82/8242.png)
