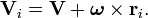Velocidade angular
Informações de fundo
SOS acredita que a educação dá uma chance melhor na vida de crianças no mundo em desenvolvimento também. Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?
- Não confundir com freqüência angular
Em física , a velocidade angular é um vector quantidade (mais precisamente, uma pseudovetor) que especifica o velocidade angular em que um objecto está a rodar juntamente com a direcção em que ele está a rodar. O Unidade SI de velocidade angular é radianos por segundo, embora possam ser medidos em outras unidades, tais como graus por segundo, expressa em graus por hora, etc. Quando medido em ciclos ou de rotações por unidade de tempo (por exemplo, rotações por minuto), ela é muitas vezes chamado a velocidade de rotação e sua magnitude o velocidade de rotação. Velocidade angular é geralmente representado pelo símbolo Omega (Ω ou ω). A direcção do vector de velocidade angular é perpendicular ao plano de rotação, num sentido que é geralmente indicado pelo regra da mão direita.
A velocidade angular de uma partícula
Duas dimensões

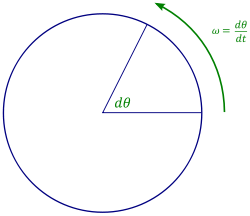
A velocidade angular de uma partícula num plano 2-dimensional é o mais fácil de se entender. Como mostrado na figura da direita (tipicamente expressa as medidas angulares φ e θ em radianos ), se desenhar uma linha desde a origem (O) para a partícula de (P), em seguida, o vector de velocidade ( 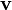 ) Das partículas terá um componente ao longo do raio (
) Das partículas terá um componente ao longo do raio ( 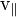 - A componente radial) e uma componente perpendicular ao raio (
- A componente radial) e uma componente perpendicular ao raio ( 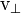 - O componente tangencial).
- O componente tangencial).
Um movimento radial produz nenhuma rotação da partícula (em relação à origem), assim, para fins de encontrar a velocidade angular do componente paralela (radial) pode ser ignorada. Por conseguinte, a rotação é completamente produzida pelo movimento tangencial (como a de uma partícula que se move ao longo de uma circunferência), e a velocidade angular é completamente determinada pela componente perpendicular (tangencial).
Pode ser visto que a taxa de mudança da posição angular da partícula está relacionada com a velocidade tangencial por:
Utilizando θ, o ângulo entre os vectores 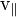 e v, ou equivalentemente como o ângulo entre os vectores P e V, dá:
e v, ou equivalentemente como o ângulo entre os vectores P e V, dá:
A combinação das duas equações acima e definir a velocidade angular dado que os rendimentos ω = dφ / dt:
Em duas dimensões da velocidade angular é um número único que não tem nenhum sentido. Um único número que não tem sentido ou é um ou um escalar pseudoscalar, a diferença é que um escalar não muda o seu sinal quando a eixos xey são trocados (ou invertida), enquanto um pseudoscalar faz. O ângulo, bem como a velocidade angular é um pseudoescalar. O sentido de rotação positivo é levado, por convenção, para ser na direcção na direcção do eixo y em relação ao eixo x. Se os eixos estão invertida, mas o sentido da rotação não o fizer, então o sinal do ângulo de rotação, e, por conseguinte, a velocidade angular, bem como, mudará.
É importante notar que a velocidade angular pseudoescalar de uma partícula depende da escolha da origem e sobre a orientação dos eixos de coordenadas.
Três dimensões
Em três dimensões, a velocidade angular se torna um pouco mais complicado. A velocidade angular, neste caso, é geralmente considerado como um vector , ou mais precisamente, uma pseudovetor. Verificou-se agora não só tem uma magnitude, mas numa direcção bem. A magnitude é a velocidade angular, e a direcção do descreve eixo de rotação. O regra da mão direita indica a direção positiva do pseudovetor velocidade angular, a saber:
- Se enrolar os dedos da mão direita para seguir o sentido de rotação, então a direcção do vector de velocidade angular é indicado pelo seu polegar direito.
Tal como no caso de duas dimensões, uma partícula tenha um componente da sua velocidade ao longo do raio a partir da origem para a partícula, e um outro componente que perpendicular ao raio. A combinação do ponto de origem e a componente perpendicular da velocidade define um plano de rotação na qual aparece o comportamento da partícula (por nesse instante) tal como acontece no caso de duas dimensões. O eixo de rotação é seguida de uma linha perpendicular a este plano, e este eixo definido na direcção do pseudovetor velocidade angular, enquanto que a magnitude é o mesmo que o valor pseudoescalar encontrado no caso 2-dimensional. Definir um vetor unitário 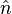 que aponta na direcção do pseudovetor velocidade angular. A velocidade angular pode ser escrita de um modo semelhante ao de duas dimensões:
que aponta na direcção do pseudovetor velocidade angular. A velocidade angular pode ser escrita de um modo semelhante ao de duas dimensões:
que, na definição do produto cruzado , pode ser escrita:
Dimensões superiores
Em geral, a velocidade angular em um espaço n-dimensional, é a derivada do tempo do tensor de deslocamento angular, que é um segundo posto inclinar-tensor simétrico. Este tensor terá n (n-1) / 2 componentes independentes e este número é a dimensão do Deite álgebra do Grupo de Lie de rotações de um espaço com produto interno n-dimensional. Acontece que, no espaço tridimensional velocidade angular pode ser representado por vector porque o número de componentes independentes é igual ao número de dimensões de espaço.
Velocidade angular de um corpo rígido

A fim de lidar com o movimento de um o corpo rígido, o melhor é considerar um sistema que é fixo em relação ao corpo rígido de coordenadas, e para estudar as transformações de coordenadas entre este e o sistema de coordenadas "de laboratório" fixo. Como mostrado na figura do lado direito, a origem do sistema de laboratório é no ponto O, a origem do sistema corpo é rígida em O "e o vector de O a O 'é R. Uma partícula (i) no corpo rígido está localizado no ponto P e o vector de posição de tal partícula é de R i no referencial de laboratório, e na posição r i na estrutura de corpo. Vê-se que a posição da partícula pode ser escrita:
A característica definidora de um corpo rígido é que a distância entre quaisquer dois pontos de um corpo rígido é inalterável no tempo. Isto significa que o comprimento do vector 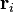 é imutável. Por Teorema de rotação de Euler, podemos substituir o vector
é imutável. Por Teorema de rotação de Euler, podemos substituir o vector 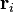 com
com 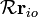 onde
onde 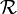 é um matriz de rotação e
é um matriz de rotação e 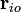 é a posição da partícula a um ponto fixo no tempo, digamos t = 0. Esta substituição é útil, porque agora é apenas a matriz de rotação
é a posição da partícula a um ponto fixo no tempo, digamos t = 0. Esta substituição é útil, porque agora é apenas a matriz de rotação 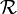 que muda no tempo e não o vector de referência
que muda no tempo e não o vector de referência 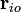 , Como o corpo rígido gira em torno do ponto O '. A posição da partícula é agora escrito como:
, Como o corpo rígido gira em torno do ponto O '. A posição da partícula é agora escrito como:
Tomando a derivada no tempo origina a velocidade da partícula:
V onde i é a velocidade da partícula (no referencial de laboratório) e V é a velocidade de O '(a origem do quadro de corpo rígido). Desde 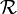 é uma matriz de rotação seu inverso sua sua transposta. Então, nós substituímos
é uma matriz de rotação seu inverso sua sua transposta. Então, nós substituímos 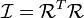 :
:
Continue tomando o tempo de derivitve 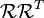 :
:
Aplicando a fórmula (AB) T = B T A T:
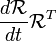 é o negativo de sua transposta. Por isso, é uma matriz 3x3 simétrica inclinação. Podemos, portanto, ter a sua dupla para obter um vector 3 dimensional.
é o negativo de sua transposta. Por isso, é uma matriz 3x3 simétrica inclinação. Podemos, portanto, ter a sua dupla para obter um vector 3 dimensional. 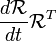 é chamado o tensor da velocidade angular . Se tomarmos a dupla deste tensor, a multiplicação de matrizes é substituído pelo produto cruzado. Sua dupla é chamado o pseudovetor velocidade angular, ω.
é chamado o tensor da velocidade angular . Se tomarmos a dupla deste tensor, a multiplicação de matrizes é substituído pelo produto cruzado. Sua dupla é chamado o pseudovetor velocidade angular, ω.
Substituindo ω na expressão velocidade acima:
Pode ser visto que a velocidade de um ponto de um corpo rígido pode ser dividida em dois termos - a velocidade de um ponto de referência fixo no corpo rígido mais o termo produto transversal com a velocidade angular da partícula em relação ao ponto de referência . Esta velocidade angular é o "spin" velocidade angular do corpo rígido, em oposição à velocidade angular do ponto de referência S 'em torno da origem O.
É um ponto importante que a velocidade angular de rotação de cada partícula do corpo rígido é o mesmo, e que a velocidade angular de rotação é independente da escolha da origem do sistema de corpo rígido ou do sistema de laboratório. Em outras palavras, é uma quantidade física real, que é uma propriedade do corpo rígido, independente da sua escolha de sistema de coordenadas. A velocidade angular do ponto de referência sobre a origem da vontade referencial de laboratório, contudo, dependem destas escolhas do sistema de coordenadas. Muitas vezes, é conveniente escolher o centro de massa do corpo rígido como a origem do sistema de corpo rígido, uma vez que uma simplificação considerável matemático ocorre na expressão para o movimento angular do corpo rígido.

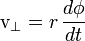
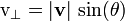
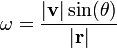
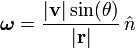
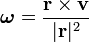
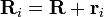
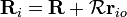
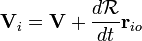
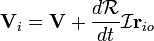
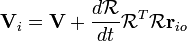
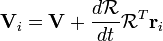
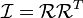
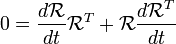
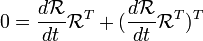
![\ Boldsymbol \ omega = [\ omega_x, \ omega_y, \ omega_z]](../../images/147/14774.png)