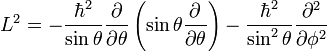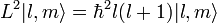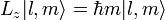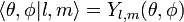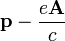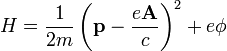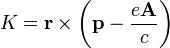O momento angular
Informações de fundo
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Visite o site da SOS Children at http://www.soschildren.org/
| A mecânica clássica |
|---|
|
Ramos
|
Formulações Mecânica analítica ( Mecânica lagrangiana Mecânica hamiltoniana) |
Conceitos fundamentais
|
Temas centrais Corpo rígido
Lei de Newton gravitação universal
Inercial / Não-inercial quadro de referência
Mecânica de planar partícula movimento
|
Movimento de rotação Movimento circular
Força centrífuga
|

Em física , o momento angular de uma partícula de cerca de uma origem é uma grandeza vectorial igual à massa da partícula multiplicado pelo produto cruzado do vector de posição da partícula com o seu vector de velocidade. O momento angular de um sistema de partículas é a soma de que as partículas de dentro dele.
O momento angular é um conceito importante, tanto física e engenharia, com inúmeras aplicações. O momento angular é importante na física porque é um quantidade conservada: o momento angular do sistema permanece constante, a menos que um externo binário actua sobre ele. Simetria rotacional de espaço está relacionada com a conservação do momento angular, como um exemplo de Teorema de Noether. A conservação do momento angular explica muitos fenômenos na natureza.
O momento angular na mecânica clássica

Definição
O momento angular de uma partícula sobre uma determinada origem é definido como:
onde:
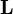 é o momento angular da partícula,
é o momento angular da partícula, 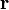 é o vector de posição da partícula em relação à origem,
é o vector de posição da partícula em relação à origem, 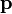 é o movimento linear da partícula, e
é o movimento linear da partícula, e 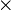 é o vector de produto cruzado .
é o vector de produto cruzado .
Como pode ser visto a partir da definição, o unidades SI derivadas de momento angular são newton medidor segundo (N · m · s ou kg · m 2 s -1). Por causa do produto cruzado, L é um pseudovetor perpendicular a ambos o vector radial r e o vector de impulso e p é atribuído um sinal pela regra da mão direita.
O momento angular de uma coleção de partículas
Se um sistema é constituído por várias partículas, o momento angular total de cerca de uma origem pode ser obtido por adição de (ou integrando) todo o momento angular das partículas constituintes. O momento angular também pode ser calculada multiplicando o quadrado do deslocamento r, a massa da partícula e a velocidade angular .
O momento angular no centro de massa
É muitas vezes conveniente considerar o momento angular de uma coleção de partículas sobre o seu centro de massa , uma vez que esta simplifica consideravelmente a matemática. O momento angular de uma colecção de partículas é a soma da quantidade de movimento angular de cada partícula:
onde 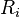 é a distância da partícula i a partir do ponto de referência,
é a distância da partícula i a partir do ponto de referência, 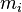 é a sua massa, e
é a sua massa, e 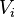 é a sua velocidade. O centro de massa é definida por:
é a sua velocidade. O centro de massa é definida por:
onde a massa total de todas as partículas é dada pela
Daqui resulta que a velocidade do centro de massa é
Se definirmos 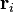 como o deslocamento de partícula i do centro de massa, e
como o deslocamento de partícula i do centro de massa, e 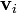 como a velocidade da partícula i em relação ao centro de massa, em seguida, temos
como a velocidade da partícula i em relação ao centro de massa, em seguida, temos
 e
e 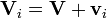
e também
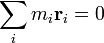 e
e 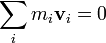
de modo a que o momento angular total está
O primeiro termo é apenas o momento angular do centro de massa. É a mesma quantidade de movimento angular pode-se obter, se houvesse apenas uma partícula de massa M em movimento a uma velocidade V localizado no centro de massa. O segundo termo é o momento angular que é o resultado das partículas em relação ao seu centro de massa em movimento. Este segundo termo pode ser simplificada ainda mais se as partículas formam um corpo rígido, caso em que um rotação aparece. Um resultado semelhante é obtido para uma distribuição contínua da matéria.
Eixo fixo de rotação
Para muitas aplicações onde um é apenas preocupado com rotação em torno de um eixo, é suficiente para descartar a natureza pseudovetor do momento angular, e tratá-lo como um escalar onde é positivo quando corresponde a uma rotação anti-horário, e no sentido horário negativo. Para fazer isso, basta levar a definição do produto cruzado e descartar o vetor de unidade, de modo a que o momento angular torna-se:
θ onde R, o símbolo p representa o ângulo entre r e p a partir de R medidos para p; uma distinção importante porque sem ele, o sinal da cruz produto não teria sentido. A partir do acima, é possível para reformular a definição de qualquer um dos seguintes:
onde 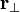 chama-se a braço distância alavanca para p.
chama-se a braço distância alavanca para p.
A maneira mais fácil de conceituar esta é considerar a distância alavanca do braço para ser a distância desde a origem até a linha que percorre p. Com esta definição, é necessário considerar a direção de p (horário pontiagudo ou anti-horário) para descobrir o sinal de L. Equivalently:
onde 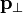 é o componente p de que é perpendicular ao r. Como acima, o sinal é decidido com base no sentido de rotação.
é o componente p de que é perpendicular ao r. Como acima, o sinal é decidido com base no sentido de rotação.
Para um objecto com uma massa fixa, que é rotativo sobre um eixo de simetria fixo, o momento angular é expressa como o produto da momento de inércia do objecto e do seu vector de velocidade angular:
onde
 é o momento de inércia do objecto (em geral, uma quantidade tensor)
é o momento de inércia do objecto (em geral, uma quantidade tensor) 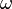 representa a velocidade angular .
representa a velocidade angular .
Como a energia cinética K de um corpo rotativo maciça é dada pela
é proporcional ao quadrado do momento angular.
Conservação do momento angular

Em um sistema fechado momento angular é constante. Esta lei de conservação segue matematicamente da simetria direcional contínuo de espaço (sem direção no espaço é diferente de qualquer outra direção). Ver Teorema de Noether.
O derivado de tempo do momento angular é chamada binário:
Assim, exigindo que o sistema para ser "fechada" aqui é matematicamente equivalente a zero binário de actuação externo no sistema:
onde 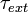 é qualquer binário aplicado ao sistema de partículas.
é qualquer binário aplicado ao sistema de partículas.
Em órbitas, o momento angular é distribuído entre o spin do próprio planeta eo momento angular de sua órbita:
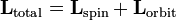 ;
;
Se um planeta se encontra a rodar mais lento do que o esperado, então os astrônomos suspeitam que o planeta é acompanhada por um satélite, porque o momento angular total é compartilhada entre o planeta e seu satélite, a fim de ser conservado.
A conservação do momento angular é usado extensivamente em analisar o que é chamado de movimento força central. Se a força resultante sobre um corpo é dirigido sempre para um ponto fixo, no centro, então não há nenhum binário sobre o corpo no que se refere ao centro, e assim o momento angular do corpo em torno do centro é constante. Momento angular constante é extremamente útil quando se lida com o órbitas dos planetas e satélites, e também quando se analisa o Modelo de Bohr do átomo .
A conservação do momento angular explica a aceleração angular de um patinador de gelo enquanto ela traz seus braços e pernas perto do eixo de rotação vertical. Ao trazer parte da massa do corpo para mais perto do eixo ela diminui momento do seu corpo de inércia. Como o momento angular é constante na ausência de torques externos, a velocidade angular (velocidade de rotação) do patinador tem de aumentar.
Os mesmos resultados fenômeno em rotação extremamente rápida de estrelas compactas (como anãs brancas , estrelas de nêutrons e buracos negros ) quando eles são formados a partir de muito maiores e mais lentos estrelas rotativas (na verdade, diminuindo o tamanho do objeto 10 4 vezes resulta em aumento de sua velocidade angular pelo fator de 10 8).
A conservação do momento angular no resultado sistema Terra-Lua na transferência de momento angular da Terra à Lua (devido ao torque de maré da Lua exerce sobre a Terra). Por sua vez, resulta na desaceleração da taxa de rotação da Terra (a cerca de 42 ns / dia), e no aumento gradual do raio da órbita da Lua (em ~ 4,5 centímetros taxa / ano).
O momento angular em mecânica relativista
Em moderna física teórica (século 20 tarde), momento angular é descrito usando um formalismo diferente. Sob esse formalismo, o momento angular é a 2 forma- Noether carga associada a invariância rotacional (Como resultado, momento angular não é conservado para espaços-tempos curvos gerais, a menos que ele passa a ser assintoticamente rotativamente invariante). Para um sistema de partículas pontuais, sem qualquer momento angular intrínseco, que acaba por ser
(Aqui, o produto cunha é usada.).
O momento angular na mecânica quântica
Na mecânica quântica , o momento angular é quantizado - isto é, não pode variar continuamente, mas apenas em " saltos quânticos "entre certos valores permitidos. O momento angular de uma partícula subatômica, devido ao seu movimento através do espaço, é sempre um múltiplo-número inteiro de 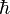 ("H-bar", conhecida como Constante de Dirac), definida como Constante de Planck dividido por 2π. Além disso, as experiências mostram que a maioria das partículas subatómicas ter, um impulso permanente incorporado angular, o que não é devido ao seu movimento através do espaço. Este rotação momento angular vem em unidades de
("H-bar", conhecida como Constante de Dirac), definida como Constante de Planck dividido por 2π. Além disso, as experiências mostram que a maioria das partículas subatómicas ter, um impulso permanente incorporado angular, o que não é devido ao seu movimento através do espaço. Este rotação momento angular vem em unidades de 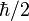 . Por exemplo, um elétron que está em repouso tem um momento angular de
. Por exemplo, um elétron que está em repouso tem um momento angular de 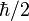 .
.
Definição básica
A definição clássica do momento angular como 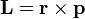 depende seis números:
depende seis números: 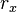 ,
, 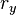 ,
, 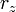 ,
, 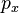 ,
, 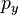 E
E 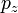 . Traduzindo isso em termos de mecânica quântica, a Princípio da incerteza de Heisenberg nos diz que não é possível para todos os seis destes números para ser medidos em simultâneo com precisão arbitrária. Portanto, não há limites para o que pode ser conhecido ou medido sobre o momento angular de uma partícula. Acontece que o melhor que se pode fazer é medir simultaneamente a magnitude do vector momento angular e seu componente ao longo de um eixo.
. Traduzindo isso em termos de mecânica quântica, a Princípio da incerteza de Heisenberg nos diz que não é possível para todos os seis destes números para ser medidos em simultâneo com precisão arbitrária. Portanto, não há limites para o que pode ser conhecido ou medido sobre o momento angular de uma partícula. Acontece que o melhor que se pode fazer é medir simultaneamente a magnitude do vector momento angular e seu componente ao longo de um eixo.
Matematicamente, o momento angular na mecânica quântica é definido como impulso - não como uma quantidade, mas como um operador na função de onda:
onde r e p são os operadores de posição e momento, respectivamente. Em particular, para uma única partícula sem carga elétrica e não rotação, o operador de momento angular pode ser escrito na base de posição como
onde  é o operador diferencial vector " Del "(também chamada de" Nabla "). Este operador momento angular orbital é a forma mais comumente encontradas do operador momento angular, embora não o único. Ela satisfaz a seguinte relações de comutação canônicos:
é o operador diferencial vector " Del "(também chamada de" Nabla "). Este operador momento angular orbital é a forma mais comumente encontradas do operador momento angular, embora não o único. Ela satisfaz a seguinte relações de comutação canônicos:
![[L_l, L_m] = i \ hbar \ sum_ {n = 1} ^ 3 \ varepsilon_ {} lmn L_n](../../images/635/63558.png) ,
,
onde ε é a lmn (antisymmetric) Símbolos de Levi-Civita. A partir deste segue
Uma vez que,
segue-se, por exemplo,
Além de momentos angulares quantificado
Dado um impulso angular total quantificado 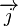 que é a soma de dois momentos angulares quantificado indivíduo
que é a soma de dois momentos angulares quantificado indivíduo 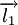 e
e  ,
,
o número quântico 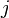 associado com o respectivo potencial pode variar desde
associado com o respectivo potencial pode variar desde  para
para  em passos inteiros onde
em passos inteiros onde 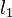 e
e 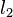 são números quânticos correspondentes às magnitudes dos momentos angulares individual.
são números quânticos correspondentes às magnitudes dos momentos angulares individual.
O momento angular como um gerador de rotações
Se 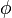 é o ângulo em torno de um eixo específico, por exemplo, o ângulo azimutal em torno do eixo z, então o momento angular ao longo deste eixo é a gerador de rotações em torno deste eixo:
é o ângulo em torno de um eixo específico, por exemplo, o ângulo azimutal em torno do eixo z, então o momento angular ao longo deste eixo é a gerador de rotações em torno deste eixo:
O autofunç~oes de L Z são, por conseguinte, 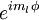 , E desde
, E desde 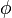 tem um período de
tem um período de  , M l deve ser um inteiro.
, M l deve ser um inteiro.
Para uma partícula com um S rotação, este leva em consideração apenas a dependência angular da localização da partícula, por exemplo a sua órbita num átomo. É portanto conhecido como momento angular orbital. No entanto, quando se faz rodar o sistema, também se altera o rodada. Por conseguinte, a momento angular total, que representa a plena gerador de rotações, é 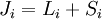 Sendo um momento angular, J satisfaz as mesmas relações de comutação como L, como a vontade explicado abaixo. a saber
Sendo um momento angular, J satisfaz as mesmas relações de comutação como L, como a vontade explicado abaixo. a saber
a partir do qual segue
Atuando com J no wavefunction 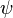 de uma partícula gera uma rotação:
de uma partícula gera uma rotação: 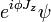 é o wavefunction
é o wavefunction 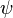 girado em torno do eixo Z por um ângulo
girado em torno do eixo Z por um ângulo 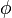 . Para uma rotação infinitesmal por um ângulo
. Para uma rotação infinitesmal por um ângulo  , O rodado wavefunction é
, O rodado wavefunction é 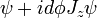 . Isto é igualmente verdade para rotações em torno de qualquer eixo.
. Isto é igualmente verdade para rotações em torno de qualquer eixo.
Em uma partícula carregada a dinâmica recebe uma contribuição do campo eletromagnético , eo angular momentos L e J alteração em conformidade.
Se o Hamiltonian é invariante sob rotações, como em problemas esfericamente simétricas, em seguida, de acordo com Teorema de Noether, que comuta com o momento angular total. Assim o momento angular total é um quantidade conservada
Desde o momento angular é o gerador de rotações, as suas relações de comutação siga as relações de comutação dos geradores do tridimensional grupo de rotação SO (3). É por isso que sempre J satisfaz estas relações comutativas. Em d dimensões, o momento angular irá satisfazer as mesmas relações de comutação como os geradores do grupo de rotação dimensional d SO (d).
SO (3) tem a mesma Álgebra de Lie (ou seja, as mesmas relações de comutação) como SU (2). Geradores de SU (2) pode ter metade inteiros valores próprios , e assim pode m 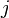 . Com efeito, para férmions a rotação S e total de impulso J angular são semi-inteiro. De facto, este é o caso mais geral: j e m
. Com efeito, para férmions a rotação S e total de impulso J angular são semi-inteiro. De facto, este é o caso mais geral: j e m 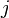 ou são números inteiros ou meias-inteiros.
ou são números inteiros ou meias-inteiros.
Tecnicamente, isso ocorre porque o cobertura universal de SO (3), isomorphic SU (2), e o representações do último são totalmente conhecidos. J i abrangem o Deite álgebra e J 2 é o Casimir invariante, e pode ser demonstrado que se os valores próprios de J e J z 2 são j e j m (J + 1), em seguida, m j e j são ambos múltiplos inteiros de metade. j é não-negativo e m j assume valores entre -j e j.
Relação com harmônicos esféricos
Operadores de momento angular geralmente ocorrem quando resolver um problema com simetria esférica em coordenadas esféricas . Então, o momento angular em representação do espaço é:
Ao resolver para encontrar eigenstates deste operador, obtemos a seguinte
onde
são o harmônicos esféricos.
O momento angular em eletrodinâmica
Ao descrever o movimento de partículas carregadas na presença de um campo eletromagnético, o "momentum cinético" p não é medir invariante. Como consequência, o momento angular canónica 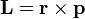 não é invariante ou medir. Em vez disso, o impulso que é física, a chamada momento canônico, é
não é invariante ou medir. Em vez disso, o impulso que é física, a chamada momento canônico, é
onde  é a carga eléctrica , c a velocidade da luz e do A potencial vetor. Assim, por exemplo, a Hamiltoniano de uma partícula carregada de massa m de um campo electromagnético é então
é a carga eléctrica , c a velocidade da luz e do A potencial vetor. Assim, por exemplo, a Hamiltoniano de uma partícula carregada de massa m de um campo electromagnético é então
onde 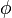 é o potencial escalar. Isto é o que dá o Hamiltoniano Lei da força de Lorentz. O impulso calibre invariante angular, ou "momento angular cinético" é dada por
é o potencial escalar. Isto é o que dá o Hamiltoniano Lei da força de Lorentz. O impulso calibre invariante angular, ou "momento angular cinético" é dada por
A interação com a mecânica quântica é discutido no artigo sobre relações de comutação canônicos.

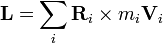
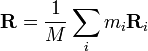
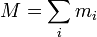
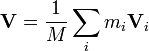
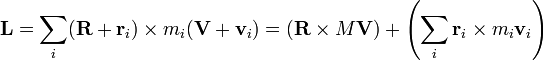
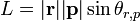
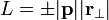
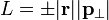
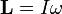
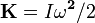
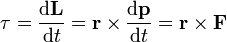
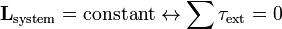
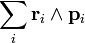
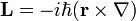
![\ Left [L_i, L ^ 2 \ right] = 0](../../images/635/63559.png)
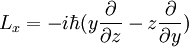
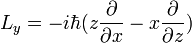
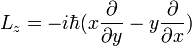
![\ Begin {align} \ left [L_x, L_y \ right] & = - \ hbar ^ 2 \ left ((y {\ \ parcial sobre \ z parcial} - z {\ \ parcial sobre \ y parcial}) (z { \ \ parcial sobre \ x parcial} - x {\ \ parcial sobre \ z parcial}) - (z {\ \ parcial sobre \ x parcial} - x {\ \ parcial sobre \ z parcial}) (y {\ partial \ over \ z parcial} - z {\ \ parcial sobre \ y parcial}) \ right) \\ & = - \ hbar ^ 2 \ left (y {\ \ parcial sobre \ x parcial} - x {\ \ parcial sobre \ y parcial} \ right) = i \ hbar L_z. \\ \ End {align}](../../images/635/63563.png)
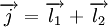
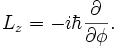
![[J_ \ ell, J_m] = i \ hbar \ sum_n \ varepsilon_ {} lmn j_n](../../images/635/63575.png)
![\ Left [J_ \ ell, J ^ 2 \ right] = 0.](../../images/635/63576.png)
![\ Left [J_L, H \ right] = 0](../../images/635/63580.png)