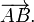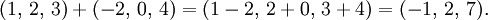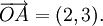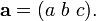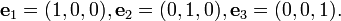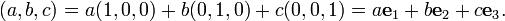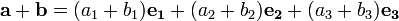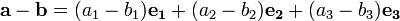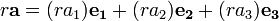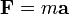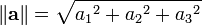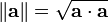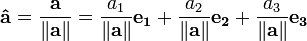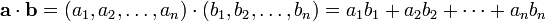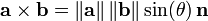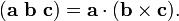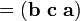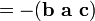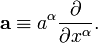Vetor

Um vector vai de A para B.

Um vector espacial, ou simplesmente vector, é um objecto geométrico que tem tanto uma magnitude e um sentido. Um vetor é freqüentemente representado por um segmento de linha que liga o ponto A inicial com o ponto B do terminal e denotado

A magnitude é o comprimento do segmento e a direcção caracteriza o deslocamento de B em relação a A: quanto se deve mover o ponto A para "carregar"-lo para o ponto B.

Muitos operações algébricas sobre números reais tem análogos próximos de vetores. Os vectores podem ser adicionadas , subtraídas , multiplicada por um número, e virado em torno de modo que a direcção seja invertida. Estas operações obedecem às leis algébricas familiares: comutatividade , associatividade , distributividade. A soma de dois vectores com o mesmo ponto inicial pode ser encontrado usando o geometricamente lei do paralelogramo. A multiplicação por um número positivo, vulgarmente chamado um escalar neste contexto, eleva-se a mudar a magnitude do vector, isto é, estiramento ou compressão que, mantendo a sua orientação; multiplicação por -1 preserva a magnitude do vector, mas inverte a sua direcção.

Coordenadas cartesianas fornecem uma maneira sistemática de descrever vectores e operações sobre eles. Um vector torna-se um triplo de números reais, os seus componentes. A adição de vetores e multiplicação de um vector por um escalar são simplesmente feito componente por componente, consulte coordenar vetor.

Vectores desempenhar um papel importante na física : velocidade e aceleração de um objecto em movimento e das forças que actuam sobre um corpo são todos descritos por vectores. Muitas outras grandezas físicas podem ser utilmente pensado como vetores. Um tem que ter em mente, contudo, que os componentes de um vetor física dependem da sistema utilizado para descrever coordenadas. Outros objetos vetoriais, como que descrevem quantidades físicas e transformar de uma forma semelhante ao abrigo mudanças do sistema de coordenadas incluem pseudovectors e tensores.

Visão global

Informalmente, um vector é uma quantidade caracterizado por um magnitude (em matemática um número, na física um número vezes uma unidade) e uma direção, muitas vezes representada graficamente por uma seta. Às vezes, fala-se de vectores ligados ou fixos, que são vetores cujo ponto inicial é o origem. Isto está em contraste com os vectores livres, que são vectores cujo ponto inicial não é necessariamente a origem.

Use em física e engenharia

Vetores são fundamentais nas ciências físicas. Eles podem ser usados para representar qualquer quantidade que tem tanto uma magnitude e direcção, tais como a velocidade , a magnitude do qual é velocidade. Por exemplo, a velocidade de 5 metros por segundo para cima pode ser representada pelo vector (0,5). Outra quantidade representada por um vector é força , uma vez que tem uma magnitude e direcção. Vectores descrevem também muitas outras grandezas físicas, tais como a deslocamento, aceleração , elétrica e campos magnéticos, dinâmica e momento angular .

Vetores no espaço cartesiano

Em coordenadas cartesianas , um vector pode ser representada pela identificação das coordenadas do ponto inicial e terminal. Por exemplo, os pontos A = (1,0,0) e B = (0,1,0) no espaço livre do vector determinar 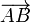que aponta a partir do ponto x = 1 no eixo x y para o ponto = 1 no eixo y.

Normalmente em coordenadas cartesianas, considera-se vectores principalmente encadernados. Um vector ligado é determinada por as coordenadas do ponto terminal, o seu ponto inicial sempre tendo as coordenadas da origem O = (0,0,0). Assim, o vector ligado representado por (1,0,0) é um vetor de unidade de comprimento que aponta desde a origem até o eixo x positivo.

A representação de coordenadas de vectores permite que as características algébricas de vectores para serem expressos de uma forma numérica conveniente. Por exemplo, a soma dos vectores (1,2,3) e (-2,0,4) é o vector

Vectores e vectores afins euclidiana

Nas configurações geométricas e físicas, às vezes é possível associar, de uma forma natural, um comprimento de vectores, bem como a noção de um ângulo entre os dois vectores. Quando o comprimento dos vectores é definido, é possível definir também um produto de ponto - um produto com valor escalar dos dois vectores de - o que dá uma caracterização algébrica conveniente de comprimento e ângulo. Em três dimensões, é ainda possível definir um produto cruzada que fornece uma caracterização algébrica de área.

No entanto, isso nem sempre é possível ou desejável para definir o comprimento de um vector de uma forma natural. Este tipo mais geral de vetor espacial é objecto de espaços vetoriais (por vectores ligados) e espaços afins (por vetores livres).

Generalizações

Em tipos mais gerais de sistemas, rotações de um vetor (e também de coordenar tensores) pode ser generalizada e categorizados de admitir uma caracterização semelhante por sua covariância e contravariância sob mudanças de coordenadas.

Em matemática , um vector é considerada mais do que uma representação de uma grandeza física. Em geral, um vector é qualquer elemento de um espaço vectorial mais de alguns campo. Os vetores espaciais deste artigo são um caso muito especial desta definição geral (eles não são simplesmente qualquer elemento de R ^d em d dimensões), que inclui uma variedade de objetos matemáticos ( álgebras, o conjunto de todas as funções de um dado domínio para uma dada linear gama, e transformações lineares). Note-se que, segundo esta definição, um tensor é um vector especial.

Representação de um vector

Os vectores são usualmente representada em negrito, tal como um. Outras convenções incluem 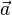ou um, especialmente na escrita. Alternativamente, alguns usam um til (~) ou um sublinhado ondulado desenhado por baixo do símbolo, que é uma convenção para indicar negrito.

Vetores geralmente são mostrados em gráficos ou outros diagramas como setas, conforme ilustrado abaixo:

Aqui, o ponto A é chamado de ponto, cauda, ou base inicial; ponto B é chamado de cabeça, ponta, ou terminal. O comprimento da seta representa a magnitude do vector, enquanto que a direcção em que os pontos de seta representa a direcção do vector.

Na figura acima, a seta também pode ser escrita como 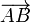ou AB.

Em um diagrama de duas dimensões, por vezes, um vector perpendicular ao plano do diagrama é desejada. Estes vectores são geralmente apresentados como pequenos círculos. Um círculo com um ponto no centro indicam um vector que aponta para fora da frente do diagrama, para o visor. Um círculo com uma cruz inscrita nele indica um vetor que aponta para dentro e para trás do diagrama. Estes podem ser pensado como uma visualização da ponta arrow frente sobre e ver as pás de uma seta na parte de trás.

Um vector no plano cartesiano, com ponto final (2,3). O próprio vector é identificado com o seu ponto de extremidade.

A fim de calcular com vectores, a representação gráfica pode ser muito complicada. Vectores de um espaço euclidiano n-dimensional pode ser representado num sistema de coordenadas cartesiano . O desfecho de um vetor pode ser identificado com uma lista de números reais n, às vezes chamado de vetor linha ou vetor coluna. Como um exemplo, em duas dimensões (ver imagem), o vetor a partir da origem O = (0,0) para o ponto A = (2,3) é simplesmente como escrito

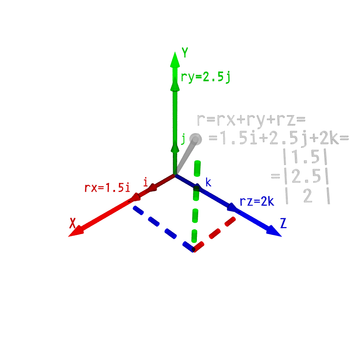
Em três dimensões do espaço Euclidiano (ou ^R3), os vectores são identificados com triplos de números correspondentes para as coordenadas cartesianas do ponto final (a, b, c). Estes números são muitas vezes dispostas num vector de vector de coluna ou linha, em particular quando se lida com matrizes , como segue:

Outra forma de expressar um vector em três dimensões é introduzir os três vectores de coordenadas básicos, por vezes referido como vectores unitários:

Estes têm a interpretação intuitiva como vetores de comprimento unidade apontando para cima os x, y, e z eixo, respectivamente. Em termos de estes, qualquer vector em R ³ pode ser expressa sob a forma:

Nota: Nas aulas de introdução à física, esses três vetores especiais são muitas vezes em vez denotado i, j, k (ou 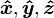quando em coordenadas cartesianas ), mas tais confrontos com a notação notação índice eo convenção somatório comumente usado em matemática de nível superior, física e engenharia. Este artigo irá optar por utilizar e _1, e _2, e _3.

A utilização de vectores unitários cartesianas 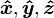como uma com base no qual a representar um vetor, não é obrigatória. Os vectores também podem ser expressas em termos de vetores unitários cilíndricos 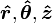ou esféricas vetores unitários 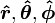. As duas últimas opções são mais convenientes para a solução de problemas que possuem simetria esférica ou cilíndrica, respectivamente.

Adição e multiplicação escalar

Igualdade Vector

Dois vectores são referidos como sendo iguais, se tiverem a mesma magnitude e direcção. No entanto, se estamos a falar de vetores livres, em seguida, dois vetores livres são iguais se eles têm o mesmo ponto de base e ponto final.

Por exemplo, o vector E ₁ + 2 e 3 + ₂ e ₃ com o ponto de base (1,0,0) e o vector e ₁ 2 e ₂ 3 e ₃ com o ponto de base (0,1,0) são diferentes vetores livres, mas a mesma (deslocamento) do vetor.

Além Vector e subtração

Deixe a = a + ₁ e ₁ a ₂ e um ₂ + ₃ e ₃ e b = ₁ e b ₁ + b ₂ + b ₂ e ₃ e _3, em que E _1, E _2, E ₃ são vectores unitários ortogonais (Nota : eles só precisam de ser linearmente independentes, isto é, não em paralelo e não no mesmo plano, para aplicar estas regras de adição e subtração algébricas)

A soma de a e b é:

A adição pode ser representada graficamente, colocando o início da seta b na ponta da seta A, e, em seguida, desenha uma seta a partir do início de uma para a ponta de b. O novo tirado da seta representa o vector de a + b, tal como ilustrado abaixo:

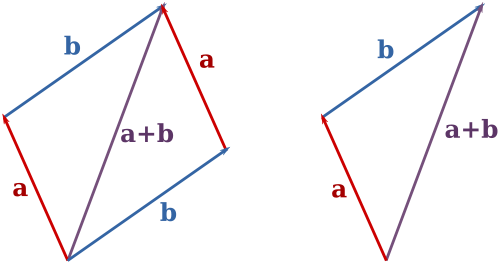
Este método de adição é muitas vezes chamado a regra paralelogramo porque a e b formam os lados de um paralelogramo e a + b é um das diagonais. Se a e b são vectores livres, então a adição é apenas definida se a e b têm o mesmo ponto de base, que, em seguida, ser também o ponto de base de a + b. Pode-se verificar geometricamente que a + b = b + a e (a + b) + c = a + (b + c).

A diferença de a e b é:

A subtracção de dois vectores podem ser geometricamente definida do seguinte modo: a partir de uma subtrair b, colocar as extremidades da a e b no mesmo ponto, e então desenhar uma seta a partir da ponta de b até a ponta de um. Isso seta representa o vector a - b, tal como ilustrado abaixo:

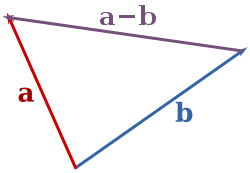
Se a e b são vetores livres, então a subtração é apenas definida se eles compartilham o mesmo ponto de base, que serão então também se tornou o ponto base da sua diferença. Esta operação merece o nome de "subtração", porque (a - b) + b = a.

Multiplicação escalar

Um vetor pode também ser multiplicado, ou re escalado, por um número real r. No contexto de vectores espaciais, estes números reais são frequentemente chamados escalares (de escala) para os distinguir dos vectores. A operação de multiplicação de um vector por um escalar é chamado multiplicação escalar. O vector resultante é:

Multiplicação escalar de um vector por um factor de 3 estende-se para fora do vector.

Intuitivamente, a multiplicação por um escalar um vector r se estende para fora por um factor de r. Geometricamente, isto pode ser visualizado (pelo menos no caso em que r é um número inteiro) como a colocação de cópias do vector r em linha, onde o ponto de extremidade de um vector é o ponto inicial da seguinte vector.

Se r for negativo, então o vetor muda de direção: ele vira em torno de um ângulo de 180 °. Dois exemplos (r = 1 e r = 2) são dadas abaixo:

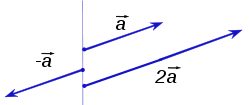
Multiplicação escalar é distributivos sobre adição de vetores no seguinte sentido: r (a + b) = r a + r b para todos os vetores a e b e todos os escalares r. Pode-se também mostram que a - b = a + (-1) b.

O conjunto de todos os vetores geométricas, juntamente com as operações de adição de vetores e multiplicação por escalar, satisfaz todos os axiomas de um espaço vetorial . Da mesma forma, o conjunto de todos os vectores ligados com um ponto de base comum forma um espaço vectorial. Este é o lugar onde o termo "espaço vetorial" se originou.

Na física, escalares também pode ter uma unidade de medida que lhes estão associados. Por exemplo, a segunda lei de Newton é

onde F tem unidades de força, um tem unidades de aceleração, ea escalar m tem unidades de massa. Numa possível interpretação física do diagrama acima, a escala de aceleração é, por exemplo, de 2 m / s ^2: cm, e que a força de 5 N: cm. Assim, uma relação de escala de 2,5 kg: 1 é utilizado para a massa. Da mesma forma, se o deslocamento tem uma escala de 1: 1000 e a velocidade de 0,2 cm: 1 m / s, ou equivalentemente, 2 ms: 1, uma proporção de 0,5: escala s é usada para o tempo.

Comprimento e o produto escalar

Comprimento de um vetor

O ou comprimento magnitude ou norma do vector é designado por um || || uma ou, menos vulgarmente, | a |, o que não deve ser confundido com o valor absoluto (um escalar "padrão").

O comprimento do vector a = a + ₁ e ₁ a ₂ e um ₂ + ₃ e ₃ em um tridimensional espaço euclidiano , em que E _1, E _2, E ₃ são vectores unitários ortogonais, pode ser calculado com a Norma euclidiana

que é uma consequência do teorema de Pitágoras desde a vetores de base e _1, e _2, e ₃ são vetores unitários ortogonais.

Isto passa a ser igual à raiz quadrada da produto escalar do vetor com ela mesma:

Comprimento e unidades Vector

Se um vector é por si só espacial, o comprimento da seta depende de um dimensionless escala. Se ele representa por exemplo uma força, a "escala" é de física dimensão comprimento / força. Assim, existe normalmente a consistência na escala entre quantidades da mesma dimensão, mas, caso contrário escala proporções podem variar; por exemplo, se "1 newton" e "5 m" são ambos representado com uma seta de 2 cm, as escamas são 1: 250 e 1 m: N 50, respectivamente. Comprimento igual de vetores de dimensão diferente não tem nenhum significado especial, a menos que haja alguma proporcionalidade constante, inerente ao sistema que o diagrama representa. Também comprimento de um vetor unitário (de comprimento dimensão, não comprimento / força, etc.) tem significado nenhum sistema invariante coordenada.

Vector unitário

Um vector de unidade é qualquer vector com um comprimento de um; geometricamente, que indica uma direcção, mas não magnitude. Se você tiver um vetor de comprimento arbitrário, você pode dividi-lo por seu comprimento para criar um vetor unitário. Isto é conhecido como um vector de normalização. Um vetor unitário é muitas vezes indicado com um chapéu como em â.

Para normalizar um vector a = [A _1, A _2, um _3], escala o vector pelo inverso do seu comprimento || || um. Isto é:

Null vector

O vector nula (ou vector zero) é o vector com comprimento zero. Escrita para fora em coordenadas, o vector é (0,0,0), e é vulgarmente designado 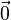, Ou 0, ou simplesmente 0. Ao contrário de qualquer outro vector, ele não tem uma direcção, e não pode ser normalizada (isto é, não existe qualquer vector de unidade que é um múltiplo do vector nulo). A soma do vector nula com uma qualquer vector é um (ou seja, 0 + a = a).

Produto de ponto

Ver artigo principal: Produto de ponto

O produto escalar de dois vetores a e b (às vezes chamado de produto interno, ou, desde que o seu resultado é um escalar, o produto escalar) é denotada por um ∙ e b é definido como:

|| || onde um e b || || denotar o norma (ou comprimento) de a e b, e θ é a medida do ângulo entre a e b (ver função trigonométrica para uma explicação de co-seno). Geometricamente, isto significa que a e b são desenhadas com um ponto inicial comum e, em seguida, o comprimento de um multiplicado pelo comprimento do referido componente de b que aponta na mesma direcção que um.

O produto de pontos, também pode ser definida como a soma dos produtos dos componentes de cada vector:

em que a e b são vectores de n dimensões, um _1, a _2, ..., a _n são coordenadas de um; e b _1, b _2, ..., b _n são coordenadas de b.

Esta operação é frequentemente útil em física ; por exemplo, o trabalho é o produto do ponto de força e deslocamento.

Produto cruzado

O produto cruzado (também chamado produto vector ou produto externo) difere do produto de pontos, principalmente, que o resultado de o produto cruzado de dois vectores é um vector. Enquanto que tudo o que foi dito acima pode ser generalizado de forma simples a mais de três dimensões, o produto cruzado é apenas significativo em três dimensões, embora o sete produto cruzado dimensional é semelhante em alguns aspectos. O produto cruzado, denotado um × b, é um vector perpendicular a ambos e a e b é definido como:

onde θ é a medida do ângulo entre a e b, e n é um vector unitário perpendicular tanto a e b. O problema com esta definição é que existem dois vectores unitários perpendiculares tanto para b e a.

Uma ilustração do produto cruzado.

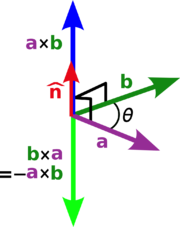
A base do vetor e _1, e _2, e ₃ é chamado destro, se os três vetores estão situados como o polegar, o dedo indicador eo dedo médio (apontando para cima de sua palma) de sua mão direita. Graficamente o produto cruzado pode ser representada pela figura da direita.

O produto de um cruzamento × b é definido de modo que a, b, e a × b torna-se também um sistema destro (mas note que a e b não são necessariamente ortogonal). Isto é o regra da mão direita.

O comprimento de um × b pode ser interpretado como a área do paralelogramo que tem a e b, como os lados.

Para escolhas arbitrárias de orientação espacial (ou seja, permitindo canhoto, bem como destro sistemas de coordenadas) o produto cruzado de dois vetores é um pseudovetor em vez de um vector (ver abaixo).

Produto triplo escalar

O produto triplo escalar (também chamado produto caixa de produto ou triplo mista) não é realmente um novo operador, mas uma maneira de aplicar os outros dois operadores de multiplicação de três vetores. O produto escalar triplo é por vezes designado por (a b c) e definido como:

Ele tem três usos primários. Primeiro, o valor absoluto do produto caixa é o volume do paralelepipédica que tem bordas que são definidas pelas três vectores. Em segundo lugar, o produto escalar triplo é zero, se e apenas se os três vectores são linearmente dependente, que pode ser facilmente comprovado pela consideração que, para os três vectores para não fazer um volume, todos eles devem assentar no mesmo plano. Em terceiro lugar, o produto da caixa é positivo se e somente se os três vetores a, b e c são destros.

Em componentes (com respeito a uma base ortonormal destro), se os três vectores são pensados como filas (ou colunas, mas na mesma ordem), o produto escalar triplo é simplesmente o determinante de a 3-a-3 da matriz tendo os três vectores como linhas. O produto triplo escalar é linear em todas as três entradas e anti-simétrica no seguinte sentido:

Os componentes do vector

Ilustração de componentes tangenciais e normais de um vector a uma superfície.

Um componente de um vector, é a influência do referido vector numa dada direcção. Os componentes são eles próprios vectores.

Um vetor é muitas vezes descrito por um número fixo de componentes que resumem a este vector exclusivamente e totalmente. Quando utilizado neste papel, a escolha das suas direcções que constituam é dependente do sistema de coordenadas em particular a ser utilizado, tal como as coordenadas cartesianas , coordenadas esféricas ou coordenadas polares . Por exemplo, o componente axial de um vector é tal que a sua componente cuja direcção é determinada por um sistema de coordenadas cartesiano eixos, enquanto radial e componentes tangenciais referem-se a raio de rotação de um objecto como a sua direcção de referência. O primeiro é paralelas ao raio e o último é ortogonal a ele. Ambos permanecem ortogonal ao eixo de rotação em todos os momentos. (Em dois dimensões esta exigência torna-se redundante como o eixo degenera para um ponto de rotação.) A escolha de um sistema de coordenadas não afecta as propriedades de um vector ou seu comportamento sob transformações.

Vectores como derivadas direccionais

Um vector pode também ser definido como um derivada direcional: considerar uma função 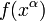e uma curva 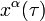. Em seguida, o derivado de direccional 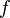é um escalar definido como

onde o índice é somados sobre o número adequado de dimensões (por exemplo de 1 a 3 no espaço euclidiano 3-dimensional, de 0 a 3 em espaço-tempo 4-dimensional, etc). Em seguida, considere um vetor tangente à :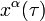

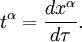
Podemos reescrever a derivada direcional em forma diferencial (sem uma determinada função 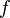) Como

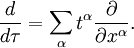
Por conseguinte, qualquer derivado direccional pode ser identificado com um vector correspondente, e qualquer vector pode ser identificado com um derivado direccional correspondente. Podemos, portanto, definir um vetor com precisão:

Vetores, pseudovectors e transformações

Uma caracterização alternativa de vetores espaciais, especialmente em física, descreve vectores como listas de quantidades que se comportam de determinada maneira sob uma transformação de coordenadas. Um vector é necessária para ter componentes que "como transformar as coordenadas" sob coordenar rotações. Em outras palavras, se a totalidade do espaço foram rodados, o vector seria rodar exactamente da mesma maneira. Matematicamente, se o sistema de coordenadas sofre uma rotação descrito por um matriz de rotação R, de modo que um vector de coordenadas x é transformado em X '= R x, em seguida, qualquer outro vector v deve ser similarmente transformada através de v' = R v. Este requisito importante é o que distingue um vetor espacial de qualquer outro tripleto de quantidades significativas fisicamente. Por exemplo, se v consiste dos x, y, e z -Componentes de velocidade , em seguida, v é um vector, porque as componentes da velocidade transformar sob coordenar alterações. Por outro lado, por exemplo, um tripleto que consiste em o comprimento, largura e altura de uma caixa rectangular poderiam ser consideradas como os três componentes de um resumo vector , mas não um vector espacial, uma vez que o quadro de rotação não correspondentemente transformar estes três componentes. Exemplos de vectores incluem deslocamento, velocidade , campo elétrico , impulso , força e aceleração .

Na linguagem de geometria diferencial , a exigência de que os componentes de um vector de transformação de acordo com a mesma matriz de transição de coordenadas é equivalente a definir um vector ser um tensor de um posto contravariant. No entanto, em geometria diferencial e de outras áreas de matemática tal como teoria da representação, os "coordenar transições" não precisa ser restrito a rotações. Outras noções de vetor espacial correspondem a diferentes opções de grupo de simetria.

Tal como um caso particular em que o grupo de simetria é importante, todos os exemplos acima são vectores que "transformam como as coordenadas" adequado e sob ambas rotações impróprias. Um exemplo de uma rotação imprópria é um espelho reflexão. Isto é, estes vectores são definidos de tal maneira que, se a totalidade do espaço foram invertidos por meio de um espelho em torno de (ou de outro modo sujeito a uma rotação indevido), que se virar em torno do vetor exactamente da mesma maneira. Vetores com esta propriedade são chamados vetores verdadeiros, ou vetores polares. No entanto, outros vectores são definidos de tal modo que, mediante a folhear um espelho, o vector vira da mesma maneira, mas também adquire um sinal negativo. Estes são chamados pseudovectors (ou vetores axiais), e ocorrem mais comumente como produtos cruzados de vetores verdadeiros.

Um exemplo de um vector axial é o momento angular . Condução em um carro , e olhando para a frente, cada uma das rodas tem um momento angular do vetor que aponta para a esquerda. Se o mundo é refletida em um espelho que muda o lado esquerdo e direito do carro, o reflexo desta angulares pontos impulso do vetor para a direita, mas o vector momento angular real da roda ainda aponta para a esquerda, correspondente ao menos assinar. Outros exemplos de pseudovectors incluir campo magnético, binário, ou mais geralmente qualquer produto cruzado de dois vectores (true).

Esta distinção entre vetores e pseudovectors é muitas vezes ignorado, mas torna-se importante no estudo de simetria propriedades. Ver paridade (física).