
Número perfeito
Fundo para as escolas Wikipédia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Para comparar instituições de caridade de patrocínio esta é a melhor ligação de patrocínio .
| ||||||||||||||||||||||
Em matemática, um número perfeito é definido como um número inteiro positivo , que representa a soma das suas positivos adequados divisores , isto é, a soma dos divisores positivos não incluindo o próprio número. De modo equivalente, um número perfeito é um número que é metade da soma de todos os seus divisores positivos, ou σ (n) = 2 n.
O primeiro número é perfeito 6, porque 1, 2 e 3 são os seus divisores positivos adequados e 1 + 2 + 3 = 6. O próximo número é perfeito 28 = 1 + 2 + 4 + 7 + 14. Os próximos números perfeitos são 496 e 8128 (sequência A000396 em OEIS ).
Estes quatro primeiros números perfeitos foram os únicos conhecidos início Matemática grega.
Mesmo números perfeitos
Euclides descobriu que os quatro primeiros números perfeitos são gerados pela fórmula 2 N -1 (2 n - 1):
- para n = 2: 2 1 (2-01 fevereiro) = 6
- para n = 3: 2 2 (fevereiro 03-01) = 28
- para n = 5: 2 4 (fevereiro 05-01) = 496
- para n = 7: 2 6 (7-01 fevereiro) = 8128.
Notando que 2 n - 1 é um número primo , em cada caso, Euclides provado que a fórmula 2 N -1 (2 n - 1) dá um número par perfeito quando n 2 - (. Euclides, Prop IX.36) 1 é primo .
Os matemáticos antigos fizeram muitas suposições sobre números perfeitos com base nos quatro sabiam, mas a maioria dessas suposições viria a revelar-se incorretas. Um desses pressupostos é que uma vez que 2, 3, 5, e 7 são, precisamente, os quatro primeiros números primos, o quinto número perfeito seria obtido quando n = 11, a quinta privilegiada. No entanto, fevereiro 11-01 = 2047 = 23 × 89 não é primo e, portanto, n = 11 não produz um número perfeito. Duas outras suposições erradas foram:
- O quinto número perfeito teria cinco dígitos de base 10 desde os primeiros quatro tinham 1, 2, 3, e 4 dígitos, respectivamente.
- Os números perfeitos se alternadamente terminam em 6 ou 8.
O quinto número perfeito ( 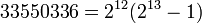 ) Tem 8 dígitos, refutando assim a primeira hipótese. Para o segundo pressuposto, o quinto número perfeito efectivamente termina com um 6. No entanto, o sexto (8 589 869 056) também termina num 6. É fácil de mostrar que o último dígito de um número qualquer, mesmo perfeita deve ser 6 ou 8 .
) Tem 8 dígitos, refutando assim a primeira hipótese. Para o segundo pressuposto, o quinto número perfeito efectivamente termina com um 6. No entanto, o sexto (8 589 869 056) também termina num 6. É fácil de mostrar que o último dígito de um número qualquer, mesmo perfeita deve ser 6 ou 8 .
Para 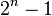 para ser nobre, é necessário, mas não suficiente que
para ser nobre, é necessário, mas não suficiente que 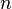 deve ser privilegiada. Os números primos da forma 2 n - 1 são conhecidos como Primos de Mersenne, após o monge do século XVII Marin Mersenne, que estudou teoria dos números e números perfeitos.
deve ser privilegiada. Os números primos da forma 2 n - 1 são conhecidos como Primos de Mersenne, após o monge do século XVII Marin Mersenne, que estudou teoria dos números e números perfeitos.
Ao longo de um milênio depois de Euclides, Ibn al-Haytham (Alhazen) por volta de 1000 dC percebi que todo número par perfeito é da forma 2 n -1 (2 n - 1), onde 2 n - 1 é nobre , mas ele não foi capaz de provar este resultado. Não era até o século 18 que Leonhard Euler provou que a fórmula 2 n -1 (2 n - 1) irá produzir todos os números até perfeitos. Assim, existe uma associação concreto de um-para-um entre os números pares perfeitos e primos Mersenne. Este resultado é muitas vezes referida como o "Euclid-Euler Teorema". A partir de setembro de 2007, apenas 44 primos de Mersenne são conhecidos, o que significa que existem 44 números perfeitos conhecidas, sendo a maior 32.582.656 × 2 (2 32.582.657 - 1) com 19.616.714 dígitos.
Os primeiros 39 números ainda são perfeitas 2 n -1 (2 n - 1) para
- n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86.243, 110.503, 132.049, 216.091, 756.839, 859.433, 1.257.787, 1.398.269, 2.976.221, 3.021.377, 6.972.593, 13.466.917 (sequência A000043 em OEIS )
Os outros 5 são conhecidos para n = 20996011, 24036583, 25964951, 30402457, 32582657. não se sabe se existem outros entre eles.
Ainda é incerto se há infinitos números primos de Mersenne e números perfeitos. A busca por novos números primos de Mersenne é o objetivo do GIMPS projeto de computação distribuída.
Uma vez que qualquer número par perfeito tem a forma 2 n -1 (2 n - 1), que é um número triangular, e, como todos os números triangulares, é a soma de todos os números naturais até um determinado ponto; neste caso: 2 n - 1. Além disso, qualquer número par perfeito excepto o primeiro, é a soma dos primeiros 2 (n-1) / 2 cubos impares:
Mesmo números perfeitos (exceto 6) dar resto 1 quando dividido por 9. Isso pode ser reformulado como segue. Adicionando os dígitos de um número qualquer, mesmo perfeito (excepto 6), em seguida, adicionando os dígitos do número resultante, e repetindo este processo até que um único dígito é obtida - o número resuting é chamado o raiz digitais - produz o número 1. Por exemplo a raiz digital 8128 = 1, já que 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, e 1 + 0 = 1.
Números perfeitos ímpares
| Existem quaisquer números perfeitos ímpares? |
Desconhece-se se há alguma números perfeitos ímpares. Vários resultados foram obtidos, mas nenhum que ajudou a localizar uma ou de outra forma resolver a questão da sua existência. Carl Pomerance apresentou uma heurística argumento que sugere que não existem números perfeitos ímpares. Além disso, foi suspeitado de que não há nenhum estranho Números harmônicas do minério. Se for verdade, isso implicaria que não existem números perfeitos ímpares.
Qualquer estranho perfeito número N devem satisfazer as seguintes condições:
- N> 10 300. Uma busca está em provar que N> 10 500 também é necessária.
- N é da forma
- onde:
- O maior fator primordial de N é maior do que 10 8 (Takeshi Goto e Yasuo Ohno, 2006).
- O segundo maior fator primordial é maior que 10 4, eo terceiro maior fator primordial é maior do que 100 (Iannucci 1999, 2000).
- N tem pelo menos 75 fatores primos; e, pelo menos, nove factores primos distintos. Se 3 não é um dos factores de N, N, em seguida, tem pelo menos 12 factores primos distintos (Nielsen 2006; Kevin Hare 2005).
- Quando
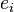 ≤ 2 para cada i
≤ 2 para cada i - O menor fator primo de N é, pelo menos, 739 (Cohen 1987).
- α ≡ 1 ( mod 12) ou α ≡ 9 (mod 12) (McDaniel, 1970).
Citação
Em 1888, Sylvester declarou:
| " | ... Uma meditação prolongada sobre o assunto satisfez-me que a existência de qualquer uma dessas [número perfeito ímpar] -sua escapar, por assim dizer, a partir da web complexo de condições que hem-lo por todos os lados-seria pouco menos que um milagre. | " |
Resultados menores
Mesmo números perfeitos têm uma forma muito precisa; números perfeitos ímpares são raros, se é que existem. Há uma série de resultados em números perfeitos que são realmente muito fácil de provar, mas mesmo assim superficialmente impressionante; alguns deles também estão sob Richard Guy forte lei dos pequenos números:
- Um número perfeito ímpar não é divisível por 105 (Kühnel 1949).
- Cada número perfeito ímpar é do formulário 12 m + 1 ou 36 m + 9 (Touchard 1953; Holdener 2002).
- O número só mesmo perfeito da forma
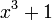 é de 28 (Makowski 1962).
é de 28 (Makowski 1962). - A Número de Fermat não pode ser um número perfeito (Luca 2000).
- Ao dividir a definição através do número perfeito N, o recíprocos dos fatores de um número perfeito N devem somar 2:
- Para 6, temos
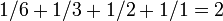 ;
; - Para 28, temos
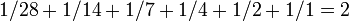 , Etc.
, Etc.
- Para 6, temos
- O número de divisores de um número perfeito (seja par ou ímpar) deve ser mesmo, uma vez que N não pode ser um quadrado perfeito.
- A partir destes dois resultados, conclui-se que cada número perfeito é um Número harmônico do minério.
Conceitos Relacionados
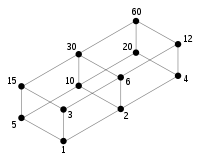
A soma dos divisores apropriados dá vários outros tipos de números. Números onde a soma é menor do que o número em si são chamados deficiente, e em que é maior do que o número, abundante. Estes termos, juntamente com a própria perfeito, vem do grego numerologia. Um par de números que são a soma de cada um dos outros divisores próprios são chamados ciclos amigáveis, e maiores de números são chamados sociável. Um número inteiro positivo tal que todo inteiro positivo menor é a soma dos divisores distintos de que é um número prático.
Por definição, um número perfeito é um ponto fixo do restrito função divisor s (n) = σ (N) - N, e o aliquota sequência associada com um número perfeito é uma constante sequência .

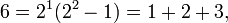
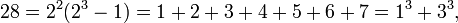
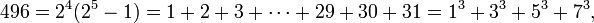
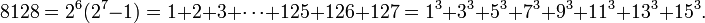
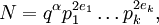
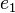 ≡
≡ 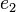 ... ≡
... ≡ 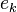 ≡ 1 (
≡ 1 ( 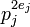 > 10 20 para alguns j (Cohen 1987).
> 10 20 para alguns j (Cohen 1987). 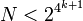 (Nielsen 2003).
(Nielsen 2003). 