Aritmética modular

Aritmética modular (às vezes chamado de módulo aritmética, ou aritmética do relógio) é um sistema de aritmética para números inteiros , onde os números "envolvente" depois de atingirem um determinado valor - o módulo. Aritmética modular foi introduzida por Carl Friedrich Gauss em seu livro Disquisitiones Arithmeticae, publicado em 1801.

Um uso familiar de aritmética modular é a sua utilização no 24 horas de relógio: a aritmética do tempo de manutenção em que o dia é executado a partir da meia-noite a meia-noite e é dividida em 24 horas, numeradas de 0 a 23. Se o tempo é agora 19:00 - 07:00 à noite - em seguida, 8 horas mais tarde será 03:00. Além habitual sugeriria que o tempo deve ser mais tarde 19 + 8 = 27, mas esta não é a resposta, porque o tempo de relógio "moldada", no final do dia. Da mesma forma, se o relógio começa às 12:00 (horas) e 21 horas decorrer, em seguida, o tempo será 9:00 no dia seguinte, em vez de 33:00. Uma vez que o número de horas começa de novo quando ele atinge 24, este é o modulo aritmética 24. Deve notar-se que neste sistema de 24:00 não é válido, porque de cada vez que seja igual a 00:00 do dia seguinte, da mesma maneira 2:60 não é um tempo válido porque é igual a 3: 00.

Tempo de manutenção em um relógio dá um exemplo de aritmética modular.

A relação de congruência

Aritmética modular pode ser tratada matematicamente através da introdução de um congruência em relação aos números inteiros que é compatível com as operações do anel de inteiros: adição , subtração e multiplicação . Para um módulo n fixa, que é definida como se segue.

Dois números inteiros a e b são ditos ser congruente módulo n, se a sua diferença a - b é um número inteiro múltiplo de n. Se este for o caso, é expresso como:

A declaração matemática acima é lido: "um é congruente com b módulo n".

Por exemplo,

porque 38-14 = 24, que é um múltiplo de 12. Para n positiva e um não-negativo e b, a congruência de a e b pode também ser pensado como afirmar que estes dois números tem a mesma resto depois dividindo pelo módulo n. Assim,

porque, quando dividido por 12, ambos os números de dar 2 como restante.

A mesma regra vale para valores negativos de um:

Uma observação sobre a notação: Porque é comum a considerar várias relações de congruência para diferentes módulos, ao mesmo tempo, o módulo é incorporado na notação. Apesar de a notação ternário, a relação de congruência para um dado módulo é binário. Isto teria sido claro se a notação de uma ≡ b _n foi utilizado, em vez da tradicional notação comum.

As propriedades que tornam esta relação uma relação de congruência (respeitando adição, subtração, multiplicação e) são os seguintes.

Se e E, em seguida:

O anel de classes de congruência

Como qualquer relação de congruência, a congruência módulo n é uma relação de equivalência , eo classe de equivalência a um número inteiro, denotada por , É o conjunto . Este conjunto, consistindo dos inteiros congruentes para um módulo n, é chamada a congruência classe ou de classe resíduo de um módulo n. Outra notação para esta classe de congruência, o que requer que no contexto do módulo é conhecido, é .

O conjunto de classes de congruência módulo n é denotado como e definido por:

Quando n ≠ 0, tem n elementos, e pode ser escrita como:

Quando n = 0, não tem zero elementos; ao contrário, é isomorfo a 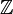, Desde .

Podemos definir adição, subtração, multiplicação e em pelos seguintes regras:

A verificação de que esta é uma definição adequada usa as propriedades dadas antes.

Desta maneira, torna-se um anel comutativo . Por exemplo, no anel , Temos

como na aritmética para o relógio de 24 horas.

A notação é utilizado, uma vez que é a fator de anel 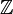pelo ideal contendo todos os inteiros divisível por n, onde é o singleton set .

Em termos de grupos, a classe de resíduo é o de uma classe lateral na grupo quociente , Um grupo cíclico .

O conjunto tem uma série de importantes propriedades matemáticas que são fundamentais para vários ramos da matemática.

Em vez de excluindo o caso especial n = 0, é mais útil incluir (Que, como já mencionado, é isomorfo ao anel 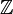de inteiros), por exemplo quando se discute a característica de um anel.

O vasilhame

A noção de aritmética modular está relacionada com a do restante em divisão . A operação de encontrar o restante é por vezes referido como o operação de módulo e podemos ver "2 = 14 (mod 12)". A diferença está no uso de congruência, indicado por ≡ e igualdade indicar por =. A igualdade implica especificamente o "resíduo comum", o membro menos não-negativa de uma classe de equivalência. Ao trabalhar com a aritmética modular, cada classe de equivalência é geralmente representado pelo seu resíduo comum, por exemplo "38 ≡ 2 (mod 12)", que pode ser encontrado usando divisão longa. Daqui resulta que, embora seja correto dizer "38 ≡ 14 (mod 12)", "2 ≡ 14 (mod 12)" e "2 ≡ 14 (mod 12)", é incorreto dizer "38 = 14 ( mod 12) "(com" = "em vez de" ≡ ").

Os parênteses são, por vezes, deixou cair a partir da expressão, por exemplo "38 ≡ 14 mod 12" ou "2 = 14 mod 12", ou colocado ao redor do divisor por exemplo, "38 ≡ 14 mod (12)". Notação como "38 (mod 12)" também tem sido observado, mas é ambígua sem esclarecimento contextual.

A relação de congruência é, por vezes expresso utilizando modulo em vez de mod, como "38 ≡ 14 (modulo 12)" em ciência da computação . A função módulo em várias linguagens de computador normalmente produzem o resíduo comum, por exemplo, a declaração "y = MOD (38,12);" dá y = 2.

Aplicações

Aritmética modular é referenciado em teoria dos números , a teoria do grupo , teoria dos anéis, teoria dos nós , álgebra abstrata , criptografia , ciência da computação , química e os visuais e musicais artes.

É um dos fundamentos da teoria dos números, tocando em quase todos os aspectos de seu estudo, e fornece exemplos importantes para a teoria do grupo, teoria dos anéis e álgebra abstrata.

Em criptografia, aritmética modular sustenta diretamente sistemas de chave pública como RSA e Diffie-Hellman, bem como fornecendo campos finitos subjacentes curvas elípticas , e é utilizado em uma variedade de algoritmos de chave simétrica, incluindo AES, IDEA, e RC4.

Em ciência da computação, aritmética modular é muitas vezes aplicado em operações bit a bit e outras operações que envolvem de largura fixa, cíclico estruturas de dados. O operação de módulo, como implementado em muitas linguagens de programação e calculadoras , é uma aplicação de aritmética modular que é frequentemente utilizado neste contexto.

Em química, o último dígito do Número de registo CAS (um número que é único para cada composto químico) é uma dígito verificador, que é calculado com base no último dígito das duas primeiras partes do Número de registo CAS vezes um, as vezes próximo dígito 2, as vezes próximo dígito 3 etc., acrescentando todos estes-se e calcular a soma módulo 10.

Nas artes visuais, a aritmética modular pode ser usado para criar padrões artísticos com base nas tabelas de multiplicação e adição modulo n (ver link externo, abaixo).

Na música, aritmética modulo 12 é usado na consideração do sistema de dodecafônica temperamento igual, onde oitava e equivalência Enarmonia ocorre (isto é, campos em uma proporção 01:02 ou 02:01 são equivalentes, e C- afiada é considerado o mesmo que D- flat).

O método de prova dos noves oferece uma verificação rápida de cálculos aritméticos decimais realizados por mão. Baseia-se no módulo aritmético modular 9, e especificamente sobre a propriedade fundamental que 10 ≡ 1 (mod 9).

De modo mais geral, a aritmética modular também tem aplicação em disciplinas como a lei (ver, por exemplo, rateio), economia , (ver, por exemplo, a teoria dos jogos ) e outras áreas do ciências sociais, onde divisão proporcional e alocação de recursos desempenha um papel central da análise.

Alguns neurologistas (ver, por exemplo, Oliver Sacks) teorizam que os chamados autistas savants utilizar uma aritmética modular "inata" para computar problemas tão complexos como que dia da semana para uma data distante irá cair sobre.

Complexidade computacional

Desde aritmética modular tem uma vasta gama de aplicações, tais, é importante saber o quão difícil é para resolver um sistema de congruências. Um sistema linear de congruencias pode ser resolvido em tempo polinomial com uma forma de eliminação de Gauss , para mais detalhes veja a teorema de congruência linear.

Resolver um sistema de equações aritméticas modular não-lineares é NP-completos. Para mais detalhes, veja por exemplo MR Garey, DS Johnson: Computadores e Intratabilidade, um Guia para a Teoria da NP-completude, WH Freeman 1979.