Teoria dos números

Teoria dos números é o ramo da matemática pura em questão com as propriedades de números e, em geral, números inteiros , em particular, bem como as classes mais amplas de problemas que surgem a partir de seu estudo.

Teoria dos números pode ser subdividido em vários campos, de acordo com os métodos utilizados e do tipo de questões investigadas. (Veja a lista de tópicos teoria dos números.)

O termo " aritmética "é também usado para se referir a teoria dos números. Este é um termo um pouco mais velhos, que já não é tão popular como era antes. Teoria dos números costumava ser chamado a aritmética mais elevada, mas isso também está caindo em desuso. No entanto, ele ainda mostra-se nos nomes de campos matemáticos ( funções aritméticas, aritmética de curvas elípticas, teorema fundamental da aritmética ). Este sentido de a aritmética termo não deve ser confundida nem com aritmética elementar , ou com o ramo da lógica que estudos Aritmética de Peano como um sistema formal. matemáticos que trabalham no campo da teoria dos números são chamados de teóricos dos números.

Ao organizar os números naturais em uma espiral e enfatizando os números primos, um padrão totalmente explicado intrigante e não é observada, o chamado Ulam espiral.

Campos

Teoria dos números elementar

Em teoria dos números elementar, números inteiros são estudadas sem o uso de técnicas de outros campos matemáticos. Questões de divisibilidade , usar da Algoritmo de Euclides para calcular maiores divisores comuns , fatorações inteiros em números primos , investigação de números perfeitos e congruências pertenço aqui. Várias descobertas importantes deste campo são Pequeno teorema de Fermat, Teorema de Euler, o Teorema restante chinês ea lei da reciprocidade quadrática. As propriedades de multiplicativos funções tais como a Função de Möbius e Função φ de Euler, sequências de números inteiros, fatoriais e os números de Fibonacci tudo também se enquadram nesta área.

Muitas perguntas na teoria dos números pode ser indicado no número de termos teóricos elementares, mas eles podem exigir muito profunda consideração e novas abordagens fora do domínio da teoria dos números elementar para resolver. Os exemplos incluem:

• A conjectura de Goldbach relativas à expressão da mesmo os números como somas de dois primos.
• A conjectura de Catalão (agora Teorema de Mihăilescu) sobre sucessivas potências inteiras.
• O conjectura dos primos gêmeos sobre a infinitude do pares Prime.
• O Collatz conjectura relativa a uma iteração simples.
• Último teorema de Fermat (declarada em 1637, mas não provou até 1994) a respeito da impossibilidade de encontrar inteiros diferentes de zero x, y, z tal que para alguns inteiro n superior a 2.

A teoria da Equações diofantinas foi mostrado mesmo para ser undecidable (veja Décimo problema de Hilbert).

Teoria analítica dos números

Teoria analítica dos números emprega a maquinaria de cálculo e análise complexa para abordar questões sobre números inteiros. O teorema de número primo (PNT) eo relacionado Hipótese de Riemann são exemplos. O problema de Waring (representando um determinado número inteiro como uma soma de quadrados, cubos, etc.), o conjectura dos primos gêmeos (encontrar infinitamente muitos pares de primeira linha com diferença 2) e conjectura de Goldbach (escrevendo inteiros pares como somas de dois números primos) estão sendo atacados com métodos analíticos bem. As provas do transcendência das constantes matemáticas, como π ou e, também são classificados como teoria dos números analítica. Enquanto declarações sobre números transcendentes pode parecer a ser removido a partir do estudo de inteiros, eles realmente estudar os possíveis valores de polinômios com coeficientes inteiros avaliados em, digamos, e; Eles também estão intimamente ligadas ao campo da Aproximação Diophantine, onde se investiga "quão bem" um determinado número real pode ser aproximada por uma racional um.

Teoria dos números algébricos

Em teoria dos números algébricos, o conceito de um número é ampliado para o algébricas que são números raízes de polinômios com racionais coeficientes. Estes domínios contêm elementos análogos aos números inteiros, a chamada inteiros algébricos. Neste cenário, as características familiares dos inteiros (por exemplo, fatoração única) não necessitam de dispor. A virtude da maquinaria employed- teoria de Galois , cohomology grupo, teoria do campo de classe, as representações do grupo e L-funções é que ele permite recuperar esse fim em parte por esta nova classe de números.

Muitos Número questões teóricas são mais atacados por estudá-los módulo p para todos números primos p (ver campos finitos). Isto é chamado de localização e que conduz à construção do números p-adic; este campo de estudo é chamado análise local e surge a partir da teoria dos números algébricos.

Teoria dos números geométricos

Teoria dos números geométricos (tradicionalmente chamado de geometria dos números) incorpora alguns conceitos geométricos básicos, tais como treliças, em questões Número de teoria. Começa com Teorema de Minkowski sobre pontos da rede em convexo define e conduz a provas fundamentais da finitude do número de classe e Teorema unidade de Dirichlet, dois teoremas fundamentais na teoria dos números algébricos.

Teoria dos números Combinatória

Combinatória teoria dos números lida com número teórico problemas que envolvem combinatórias idéias em suas formulações ou soluções. Paul Erdős é o principal fundador deste ramo da teoria dos números. Tópicos típicos incluem sistema de cobertura, problemas de soma zero, vário sumsets restritas, e progressões aritméticas em um conjunto de inteiros. Métodos algébricos ou analíticas são poderosos neste campo.

Teoria dos números Computacional

Teoria dos números computacional estuda algoritmos relevantes na teoria dos números. Algoritmos rápidos para testes privilegiada e fatoração inteiro tem importantes aplicações em criptografia .

História

Teoria dos números védica

Matemáticos em Índia estavam interessados em encontrar soluções integrais de Equações diofantinas desde a Era védica. O primeiro uso geométrica de equações diofantinas pode ser rastreada até a Sulba Sutras, que foram escritos entre os séculos 8 e 6 aC. Baudhayana (c. 800 aC) encontrou dois conjuntos de soluções positivas para um conjunto de equações diofantinas simultâneas, e também utilizou as equações diofantinas simultâneas com até quatro incógnitas. Apastamba (c. 600 aC) utilizou as equações diofantinas simultâneas com até cinco incógnitas.

Teoria dos números Jaina

Na Índia, Matemáticos Jaina desenvolveu a primeira teoria sistemática dos números do quarto século aC ao século 2 dC. (. C 400 aC) O texto Jaina Surya Prajinapti classifica todos os números em três conjuntos: enumeráveis, inúmeras e infinitas. Cada uma delas foi subdividido em três ordens:

• Enumerable: mais baixo, intermediário e alto.
• Inumeráveis: quase inumeráveis, verdadeiramente inumeráveis e innumerably inumeráveis.
• Infinito: quase infinita, verdadeiramente infinito, infinitamente infinita.

Os jainistas foram os primeiros a descartar a idéia de que todos os infinitos eram os mesmos ou igual. Eles reconheceram cinco tipos diferentes de infinito: infinito em um e dois sentidos (um dimensão), infinito em área (duas dimensões), infinito em todos os lugares (três dimensões), e infinito perpetuamente (número infinito de dimensões).

O maior número N enumeráveis dos jainistas corresponde ao conceito moderno de aleph-nulo 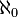(O número cardinal do conjunto infinito de números inteiros 1, 2, ...), a menor cardinal número transfinito. O jainistas também definiu todo um sistema de números cardinais transfinitos, dos quais 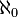é o menor.

No trabalho Jaina na teoria dos conjuntos , dois tipos básicos de números transfinitos são distinguidas. Em ambos físico e fundamentos ontológicos, foi feita uma distinção entre asmkhyata e ananata, entre infinidades rigidamente limitadas e pouco limitadas.

Teoria dos números grego

Teoria dos números foi um estudo favorito entre a Matemáticos gregos do período helenístico tardio (3 século dC) em Alexandria , Egito , que estavam cientes da Diophantine conceito equação em numerosos casos especiais. O primeiro matemático grego para estudar estas equações foi Diofanto.

Diofanto também procurou um método de encontrar soluções inteiras para linear equações indeterminadas, equações que não possuem informações suficientes para produzir um único conjunto discreto de respostas. A equação é tal equação. Diofanto descobriu que muitas equações indeterminadas pode ser reduzido a um formulário onde uma determinada categoria de respostas é conhecido, embora uma resposta específica não é.

Teoria dos números clássica indiana

Equações diofantinas foram extensivamente estudadas por matemáticos na Índia medieval, que foram os primeiros a investigar sistematicamente os métodos de determinação de soluções de equações diofantinas. Aryabhata (499) deu a primeira descrição explícita da solução integral geral da equação linear Diophantine um b C, que ocorre no seu texto Aryabhatiya. Este algoritmo kuttaka é considerada uma das contribuições mais significativas de Aryabhata em matemática pura, que encontraram soluções para equações diofantinas por meio de frações contínuas. A técnica foi aplicada por Aryabhata para dar soluções integrais de equações diofantinas lineares simulataneous, um problema com importantes aplicações em astronomia. Ele também encontrou a solução geral para o indeterminado equação linear utilizando este método.

Brahmagupta em 628 tratadas equações diofantinas mais difíceis. Ele usou o chakravala método para resolver quadrática equações diofantinas, incluindo formas de Equação de Pell, tal como . Sua Brahma Sphuta Siddhanta foi traduzido para o árabe em 773 e foi posteriormente traduzido para o latim em 1126. A equação mais tarde foi colocada como um problema em 1657 pelo francês matemático Pierre de Fermat . A solução foi encontrada geral para esta forma particular da equação de Pell mais de 70 anos mais tarde por Leonhard Euler , enquanto que foi encontrada a solução geral para a equação de Pell mais de 100 anos mais tarde por Joseph Louis Lagrange em 1767. Enquanto isso, há muitos séculos atrás, a solução geral para A equação de Pell foi gravado por Bhaskara II em 1150, utilizando uma versão modificada do método chakravala de Brahmagupta, que ele também utilizado para encontrar a solução geral para outras equações indeterminadas e equações diofantinas quadrática. Chakravala método de Bhaskara para encontrar a solução geral para a equação de Pell era muito mais simples do que o método utilizado pelo Lagrange mais de 600 anos mais tarde. Bhaskara também encontrou soluções para outra quadrática indeterminado, cúbico, quartic, e de ordem superior polinomiais equações. Narayana Pandit melhorada no método chakravala e encontraram soluções mais gerais para outros quadrática indeterminado e de ordem superior equações polinomiais.

Teoria dos números Islâmica

A partir do século 9, Matemática islâmicos tinha um grande interesse na teoria dos números. O primeiro destes era matemáticos Thabit ibn Qurra, que descobriu um algoritmo que permitiu pares de números amigáveis para ser encontrada, ou seja, dois números, tais que cada um deles é a soma dos divisores apropriados da outra. No século 10, Al-Baghdadi olhou para uma ligeira variante do método de Thabit ibn Qurra.

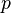No século 10, al-Haitham parece ter sido o primeiro a tentar classificar todos os mesmo números perfeitos (números iguais à soma de seus divisores próprios) como os da forma onde é primo. Al-Haytham também é a primeira pessoa a declarar Teorema de Wilson, ou seja, que se p é primo, então é divisível por . Não está claro se ele sabia como provar este resultado. Ele é chamado de teorema de Wilson por causa de um comentário feito por Edward Waring em 1770 que John Wilson tinha notado o resultado. Não há nenhuma evidência de que John Wilson sabia como provar isso e certamente Waring não o fez. Lagrange deu a primeira prova em 1771.

Números amigáveis desempenhou um grande papel na matemática islâmicos. No século 13, Matemático persa Al-Farisi deu uma nova prova do teorema de Thabit ibn Qurra, introduzindo novas ideias importantes sobre fatoração e métodos combinatórios. Ele também deu o par de números amigáveis 17296, 18416, que têm sido atribuídos a Euler, mas sabemos que estes eram conhecidos mais cedo do que al-Farisi, talvez até por Thabit ibn-se Qurra. No século 17, Muhammad Baqir Yazdi deu o par de números amigáveis 9.363.584 e 9.437.056 ainda muitos anos antes contribuição de Euler.

Teoria dos números Europeu início

Teoria dos números começou em Europa nos séculos 16 e 17, com François Viète, Bachet de Meziriac e, especialmente, Fermat , cujas método descida infinita foi a primeira prova geral de perguntas diofantinas. último teorema de Fermat foi colocada como um problema em 1637, uma prova de que não foi encontrado até 1994. Fermat também posou a equação como um problema em 1657.

No século XVIII, Euler e Lagrange fez importantes contribuições à teoria dos números. Euler fez alguns trabalhos em teoria analítica dos números, e encontrou uma solução geral para a equação . Lagrange encontrou uma solução para a equação mais geral de Pell. Euler e Lagrange resolvido estas equações Pell por meio de frações contínuas, embora este foi mais difícil do que o indiano método chakravala.

Começo da teoria dos números moderno

Por volta do início dos livros do século XIX de Legendre (1798), e Gauss juntar as primeiras teorias sistemáticas na Europa. Gauss de Disquisitiones Arithmeticae (1801) pode ser dito para começar a moderna teoria dos números.

A formulação da teoria do congruências começa com Disquisitiones de Gauss. Ele introduziu o simbolismo

e explorou a maior parte do campo. Chebyshev publicado em 1847 um trabalho em russo sobre o assunto, e na França Serret popularizou.

Além de resumir o trabalho anterior, Legendre, afirmou o lei da reciprocidade quadrática. Esta lei, descoberto por indução e enunciada por Euler, foi provado pela primeira vez por Legendre em seu Théorie des Nombres (1798) para casos especiais. Independentemente de Euler e Legendre, Gauss descobriu a lei sobre 1795, e foi o primeiro a dar uma prova geral. O seguinte também contribuíram para o assunto: Cauchy; Dirichlet cujas Vorlesungen über Zahlentheorie é um clássico; Jacobi, que introduziu a Jacobi símbolo; Liouville, Zeller (?), Eisenstein, Kummer, e Kronecker. A teoria estende para incluir e cúbico quartic reciprocidade, (Gauss, Jacobi que primeiro revelou a lei da reciprocidade cúbica, e Kummer).

Para Gauss é também devido a representação de números de binário formas quadráticas.

Teoria dos números primos

Um tema recorrente e produtiva na teoria dos números é o estudo da distribuição dos números primos. Carl Friedrich Gauss conjecturou o limite do número de primos que não excedam um determinado número (o teorema de número primo) como um adolescente.

Chebyshov (1850) deu limites úteis para o número de números primos entre dois limites indicados. Riemann introduziu análise complexa na teoria do Função zeta de Riemann. Isto levou a uma relação entre os zeros da função zeta e da distribuição dos números primos, acabou levando a uma prova de teorema de número primo de forma independente por Hadamard e de la Vallée Poussin em 1896. No entanto, uma prova elementar foi dado mais tarde por Paul Erdős e Atle Selberg em 1949. Aqui meios elementares que não utilizam técnicas de análise complexa; no entanto, a prova ainda é muito engenhoso e difícil. O Hipótese de Riemann, o que daria informações muito mais precisas, ainda é uma questão em aberto.

Desenvolvimentos do século XIX

Cauchy, Poinsot (1845), Lebesgue (1859, 1868), e, nomeadamente, Hermite ter acrescentado ao assunto. Na teoria das formas ternários, Eisenstein tem sido um líder, e para ele e HJS Smith também é devido um avanço notável na teoria das formas em geral. Smith deu uma classificação completa das formas quadráticas ternárias, e estendeu as pesquisas de Gauss relativas reais formas quadráticas para formas mais complexas. As investigações relativas à representação de números pela soma de 4, 5, 6, 7, 8 quadrados foram avançados por Eisenstein ea teoria foi completado por Smith.

Dirichlet foi o primeiro a palestra sobre o assunto em uma universidade alemã. Entre suas contribuições é a extensão do último teorema de Fermat :

que Euler e Legendre tinha provado para (E, portanto, por implicação, todos os múltiplos de 3 e 4), mostrando que Dirichlet . Entre os escritores franceses são posteriores Borel; Poincaré, cujas memórias são numerosos e valiosos; Tannery, e Stieltjes. Entre os principais contribuintes na Alemanha eram Kronecker, Kummer, Schering, Bachmann, e Dedekind. Na Áustria Vorlesungen Arithmetik de Stolz über allgemeine (1885-1886), e na Inglaterra Teoria Mathews 'de Números (Parte I, 1892) eram obras acadêmica em geral. Genocchi, Sylvester, e JWL Glaisher também contribuíram para a teoria.

Desenvolvimentos do século XX e início do XIX

Era a época de grandes avanços na teoria dos números, devido ao trabalho de Axel Thue em equações diofantinas, de David Hilbert em teoria dos números algébricos (ele também provou a Número conjectura primeiro-Waring), e para a criação de teoria dos números geométrico por Hermann Minkowski, mas também graças à Adolf Hurwitz, Georgy F. Voronoy, Waclaw Sierpinski, Derrick Norman Lehmer e vários outros.

Desenvolvimentos do século XX

As principais figuras na teoria dos números do século XX incluem Hermann Weyl, Nikolai Chebotaryov, Emil Artin, Erich Hecke, Helmut Hasse, Alexander Gelfond, Yuri Linnik, Paul Erdős, Gerd Faltings, GH Hardy, Edmund Landau, Louis Mordell, John Edensor Littlewood, Srinivasa Ramanujan, André Weil, Ivan Vinogradov, Atle Selberg, Carl Ludwig Siegel, Igor Shafarevich, John Tate, Robert Langlands, Goro Shimura, Kenkichi Iwasawa, Jean-Pierre Serre, Pierre Deligne, Enrico Bombieri, Alan Baker, Peter Swinnerton-Dyer, Bryan Birch, Vladimir Drinfeld, Laurent Lafforgue, Andrew Wiles, e Richard Taylor.

Marcos na teoria dos números do século XX incluem a prova do Último Teorema de Fermat por Andrew Wiles em 1994 ea prova da afins Taniyama-Shimura em 1999.

Cotações

• A matemática é a rainha das ciências e teoria dos números é a rainha da matemática -. Gauss
• Deus inventou os números inteiros; tudo o resto é obra do homem. - Kronecker