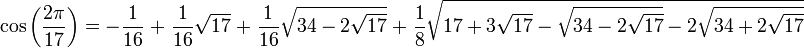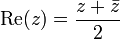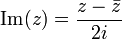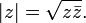Règle et au compas constructions

Création d'un hexagone régulier avec une règle et au compas

Construction d'un pentagone régulier

Compass et-règle ou la construction règle et compas est la construction de longueurs, angles , et d'autres figures géométriques en utilisant seulement une idéalisée règle et boussole.

La règle idéalisé, connu sous le nom règle, est supposé avoir une longueur infinie, et n'a pas de marques sur lui et un seul bord. La boussole est supposé se effondrer lorsque levée de la page, donc ne peut pas être directement utilisé pour transférer des distances. (Ceci est un peu importante restriction, comme cela peut être réalisé par l'intermédiaire du boussole théorème d'équivalence.) Plus formellement, les seules constructions permises sont celles accordées par Euclide trois premiers postulats s '.

Chaque constructible de point en utilisant la règle et compas peut être construit en utilisant la boussole seul. Un certain nombre de problèmes anciens en géométrie plane imposer cette restriction.

Les plus célèbres problèmes règle et à la boussole ont été avéré impossible dans plusieurs cas par Pierre Wantzel, en utilisant la mathématique théorie des champs. En dépit de preuves existantes d'impossibilité, certains persistent à essayer de résoudre ces problèmes. Beaucoup de ces problèmes sont faciles à résoudre à condition que d'autres transformations géométriques sont autorisés: par exemple, doubler le cube est possible en utilisant des constructions géométriques, mais pas possible en utilisant la règle et compas seul.

Mathématicien Underwood Dudley a fait une marge de collecte de fausses preuves règle et à la boussole, ainsi que d'autres travaux de mathématique manivelles, et les a recueillies dans plusieurs livres.

outils de règle et au compas

Une boussole

Les "boussole" et "règle" de règle et au compas constructions sont idéalisations de règles et compas dans le monde réel:

• La boussole peut être ouvert arbitrairement large, mais (contrairement à certains réel compas), il n'a pas de marques sur elle. Cercles ne peuvent être dessinées à l'aide de deux points existants qui donnent le centre et un point sur le cercle. La boussole se effondre lorsqu'il ne est pas utilisé pour le dessin, il ne peut pas être utilisé pour copier une longueur à un autre endroit.
• La règle est infiniment long, mais il n'a pas de marques sur lui et a un seul bord, contrairement dirigeants ordinaires. Il ne peut être utilisé pour dessiner un segment de ligne entre deux points ou pour prolonger une ligne existante.

La boussole moderne généralement ne se effondre pas et plusieurs constructions modernes utiliser cette fonction. Il semblerait que la boussole est un instrument moderne "plus puissant" que la boussole antique. Cependant, par la proposition 2 du Livre 1 de Éléments d'Euclide , aucune puissance de calcul est perdu en utilisant une telle boussole se effondrer; il ne est pas nécessaire de transférer une distance d'un endroit à un autre. Bien que la proposition est correcte, ses preuves ont une histoire longue et mouvementée.

Chaque construction doit être exact. «À l'œil», il (essentiellement en regardant la construction et deviner à sa précision, ou en utilisant une certaine forme de mesure, tels que les unités de mesure sur une règle) et se approcher ne compte pas comme une solution.

Chaque construction doit se terminer. Ce est, il doit avoir un nombre fini d'étapes, et ne pas être la limite d'approximations plus en plus étroits.

Dit de cette façon, règle et au compas constructions semblent être une jeu de société, plutôt que d'un grave problème pratique; mais le but de la restriction est de se assurer que les constructions peuvent être prouvées pour être tout à fait exact, et est donc important à la fois à l'élaboration (conception à la fois par logiciel de CAO et de la rédaction traditionnelle avec un crayon, du papier, règle et compas) et la science des poids et mesures, dans lesquelles la synthèse exacte de cadavres ou de matériaux de référence est extrêmement important. L'un des objectifs principaux des mathématiques grecques était de trouver constructions exactes de différentes longueurs; par exemple, le côté d'un pentagone inscrit dans un cercle donné. Les Grecs ne pouvaient trouver constructions pour les trois problèmes:

• La quadrature du cercle: dessiner un carré la même zone comme un cercle donné.
• Doubler le cube: Dessin d'un cube avec deux fois le volume d'un cube donné.
• Trisection de l'angle: Division d'un angle donné en trois petits angles tous de la même taille.

Depuis 2000 ans, les gens ont essayé de trouver des constructions dans les limites fixées ci-dessus, et qui ont échoué. Tous les trois ont maintenant été prouvé en vertu des règles mathématiques impossible général (angles avec certaines valeurs peuvent être trisected, mais pas tous les angles possibles).

Les constructions de base

Les constructions de base

Tous règle et au compas constructions consistent en l'application répétée de cinq constructions de base en utilisant les points, lignes et cercles qui ont déjà été construits. Ceux-ci sont:

• Création de la ligne à travers deux points existants

• Création du cercle passant par un point avec le centre un autre point

• Création du point qui est l'intersection de deux lignes existantes, non parallèles

• Création d'une ou des deux points dans l'intersection d'une ligne et un cercle (se ils se croisent)

• Création d'une ou des deux points dans l'intersection des deux cercles (se ils se croisent).

Par exemple, en commençant avec seulement deux points distincts, nous pouvons créer une ligne ou l'un des deux cercles (à tour de rôle, en utilisant chaque point comme le centre et passant par l'autre point). Si nous tirons deux cercles, deux nouveaux points sont créés à leurs intersections. Dessin lignes entre les deux points d'origine et l'un de ces nouveaux points achève la construction d'un triangle équilatéral.

Par conséquent, dans tout problème géométrique, nous avons un ensemble initial de symboles (points et lignes), un algorithme, et certains résultats. Dans cette perspective, la géométrie est équivalent à une axiomatique algèbre , en remplacement de ses éléments par des symboles. Probablement Gauss a réalisé ce premier, et l'a utilisé pour prouver l'impossibilité de certaines constructions; que beaucoup plus tard ne Hilbert trouver un ensemble complet de axiomes de la géométrie.

Les points constructibles et longueurs

Trisection un segment avec règle et au compas.

Preuve formelle

Il ya beaucoup de façons différentes pour prouver quelque chose est impossible. Une preuve plus rigoureuse serait de délimiter la limite du possible, et de montrer que pour résoudre ces problèmes, il faut transgresser cette limite. Une grande partie de ce qui peut être réalisé est recouvert en théorie interception.

Nous pourrions associer une algèbre à notre géométrie à l'aide d'un système de coordonnées cartésiennes en deux lignes, et de représenter les points de notre plan par vecteurs. Enfin, nous pouvons écrire ces vecteurs comme les nombres complexes.

En utilisant les équations pour les lignes et les cercles, on peut montrer que les points sur lesquels ils se croisent dans un mensonge extension quadratique de la plus petite zone F contenant deux points sur la ligne, le centre du cercle, et le rayon du cercle. Autrement dit, ils sont de la forme , Où x, y et k sont F.

Comme le champ de points constructibles est fermé sous des racines carrées, elle contient tous les points qui peuvent être obtenus par une suite finie d'extensions quadratiques du champ de nombres complexes à coefficients rationnels. Par le paragraphe ci-dessus, on peut montrer que ne importe quel point constructible peut être obtenu par une telle séquence d'extensions. Comme corollaire de cela, on constate que le degré du polynôme minimal pour un point (et donc de ne importe quelle longueur constructible) constructible est une puissance de 2. En particulier, tout point constructible (ou longueur) est un nombre algébrique, mais pas tous les nombres algébriques est constructible (à savoir la relation entre les longueurs constructibles et nombres algébriques ne est pas bijective); par exemple, est algébrique mais pas constructible.

Angles constructibles

Il y a un bijection entre les angles qui sont constructible et les points qui sont constructible sur ne importe quel cercle constructible. Les angles qui sont sous forme d'une constructible groupe abélien sous addition modulo 2π (qui correspond à la multiplication des points sur le cercle unité considérées comme des nombres complexes). Les angles qui sont constructible sont exactement celles dont la tangente (ou de manière équivalente, sinus ou cosinus) est constructible comme un nombre. Par exemple, la régulière Heptadécagone est constructible parce

découverte par Gauss .

Le groupe d'angles constructibles est fermé sous l'opération qui divise par deux angles (qui correspond à la prise des racines carrées). Les seuls angles d'ordre fini qui peuvent être construits à partir de deux points sont ceux dont l'ordre est soit une puissance de deux, ou un produit d'une puissance de deux et un ensemble de distincte Fermat amorce. En outre, il est un ensemble dense d'angles constructibles d'ordre infini.

Règle et au compas constructions que l'arithmétique complexe

Étant donné un ensemble de points dans le plan euclidien , en sélectionnant l'un d'eux d'être appelé 0 et une autre d'être appelé une, avec un choix arbitraire de orientation nous permet de considérer les points comme un ensemble de nombres complexes .

Étant donné une telle interprétation d'un ensemble de points que les numéros complexes, les points constructibles utilisant règle et au compas constructions valides seuls sont précisément les éléments de la plus petite champ contenant l'ensemble original de points et fermé sous la conjugués et complexes racine carrée opérations (pour éviter toute ambiguïté, nous pouvons spécifier la racine carrée avec argumentation complexe inférieure à π). Les éléments de ce domaine sont précisément ceux qui peut être exprimée par une formule dans les points originaux en utilisant uniquement les opérations de plus , la soustraction , la multiplication , la division , conjugué complexe, et la racine carrée , qui est facilement considérée comme un sous-ensemble dénombrable dense de l'avion. Chacun de ces six opérations correspondant à une simple boussole et la construction règle. De cette formule, il est facile de produire une construction du point correspondant, en combinant les constructions pour chacune des opérations arithmétiques. Constructions plus efficaces d'un ensemble particulier de points correspondent à des raccourcis dans ces calculs.

Équivalente (et sans avoir besoin de choisir arbitrairement deux points) nous pouvons dire que, étant donné un choix arbitraire de l'orientation, un ensemble de points détermine un ensemble de rapports complexes fournies par les rapports des différences entre deux paires de points. L'ensemble des ratios constructible utilisant règle et au compas d'un tel ensemble de ratios est précisément le plus petit champ contenant les rapports originaux et fermé sous prenant conjugués complexes et les racines carrées.

Par exemple, la partie réelle, partie imaginaire et le module d'un point ou rapport z (en prenant l'un des deux points de vue ci-dessus) sont constructible car elles peuvent être exprimées en

Doubler le cube et trisection d'un angle (sauf pour les angles spéciaux tels que tout φ telle que φ / 6π est un nombre rationnel avec dénominateur le produit d'une puissance de deux et un ensemble de distincte Nombres premiers de Fermat) nécessitent des ratios qui sont la solution à équations cubiques, tandis que la quadrature du cercle a besoin d'un rapport transcendantal. Aucun d'entre eux sont dans les domaines décrits, par conséquent, aucune règle et au compas construction pour ces existe.

Constructions impossibles

Les trois problèmes de construction suivantes, dont les origines remontent à l'antiquité grecque, ont été considérées comme impossible dans le sens où ils ne pouvaient pas être résolus en utilisant uniquement la règle et au compas. Avec les méthodes mathématiques modernes cette "considération" des mathématiciens grecs peut être se est avéré être correct. Les problèmes eux-mêmes, cependant, sont réalisables, et les Grecs savaient comment les résoudre, sans la contrainte de travailler seulement avec règle et compas.

La quadrature du cercle

Le plus célèbre de ces problèmes, la quadrature du cercle, autrement connu comme la quadrature du cercle, consiste à construire un carré avec la même zone comme un cercle donné en utilisant uniquement la règle et compas.

La quadrature du cercle a été prouvé impossible, car il implique la génération d'un nombre transcendant, ce est- 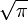. Seuls certains nombres algébriques peuvent être construits avec règle et au compas seul, à savoir ceux qui sont construits à partir des nombres entiers avec une séquence fini d'opérations d'addition, soustraction, multiplication, division, et en prenant des racines carrées. L'expression «quadrature du cercle» est souvent utilisé pour signifier «faire l'impossible" pour cette raison.

Sans la contrainte d'exiger solution en règle et au compas seul, le problème est facilement résoluble par une grande variété de moyens géométriques et algébriques, et a été résolu de nombreuses fois dans l'antiquité.

Doubler le cube

Doubler le cube: en utilisant seulement une règle et compas, construire le côté d'un cube qui a deux fois le volume d'un cube avec un côté donné. Ce est impossible parce que la racine cubique de deux, si algébrique, ne peut pas être calculée à partir des nombres entiers par addition, soustraction, multiplication, division, et en prenant des racines carrées. Cela fait suite parce que sa polynôme minimal sur les rationnels est de degré 3. Cette construction est possible en utilisant une règle avec deux marques sur elle et une boussole.

Angle trisection

Angle trisection: en utilisant seulement une règle et un compas, construire un angle qui est un tiers d'un angle arbitraire donné. Ce est impossible dans le cas général. Par exemple: si l'angle de π / 3 radians (60 ° ) ne peut pas être trisected, l'angle 2π / 5 radians (72 ° = 360 ° / 5) peuvent être trisected. Ce problème est également résolu facilement quand une règle avec deux marques sur elle est autorisée (a Construction de neusis).

Construction de polygones réguliers

Construction d'un carré.

Certains polygones réguliers (par exemple, un pentagone) sont faciles à construire avec règle et le compas; d'autres non. Cela a conduit à la question: Est-il possible de construire tous les polygones réguliers avec règle et le compas?

Carl Friedrich Gauss en 1796 a montré qu'un n régulière -sided polygone peut être construit avec règle et le compas si l'étrange facteurs premiers de n sont distincts Fermat amorce. Gauss conjecturé que cette condition était également nécessaire, mais il n'a offert aucune preuve de ce fait, qui a été fourni par Pierre Wantzel en 1837.

Construire avec seulement règle ou seule boussole

Il est possible (en fonction de la Mohr-Mascheroni théorème) de construire quoi que ce soit avec juste une boussole se il peut être construit avec une règle et au compas, à condition que les données indiquées et les données que l'on trouve sont constitués de points discrets (pas de lignes ou cercles). Il est impossible de prendre une racine carrée avec juste une règle, de sorte que certaines choses qui ne peuvent être construits avec une règle peut être construit avec une boussole; mais (par la Poncelet-Steiner théorème) donné un seul cercle et son centre, ils peuvent être construits.

Constructions étendues

Dirigeants remarquable

Archimède et Apollonios donné constructions impliquant l'utilisation d'un dirigeant remarquable. Cela leur permettra, par exemple, de prendre un segment de ligne, deux lignes (ou cercles), et un point; puis tracer une ligne qui passe par le point donné et coupe les deux lignes, et telle que la distance entre les points d'intersection est égale à la segment donné. Ce que les Grecs appelaient neusis («inclinaison», «tendance» ou «frisant»), parce que la nouvelle ligne tend à point. Dans ce schéma élargi, ne importe quelle distance dont le rapport à une distance existante est la solution d'un ou un cube équation quartique est constructible. Il se ensuit que, si les dirigeants marquables et neusis sont autorisés, le trisection de l'angle (voir Archimède la trisection) et la duplication du cube peuvent être atteints; la quadrature du cercle est encore impossible. Certains des polygones réguliers, comme le heptagone, devenu constructible; et John H. Conway donne constructions pour plusieurs d'entre eux; mais le polygone face 11, la hendécagone, est encore impossible, et infiniment beaucoup d'autres.

Lorsque seulement une trisectrice angle est autorisé, il ya une description complète de tous les polygones réguliers qui peuvent être construits, y compris ci-dessus mentionnée régulière heptagone, triskaidecagon (13-gon) et Ennéadécagone (19-gon). Il est ouvert se il existe une infinité de nombres premiers p pour lequel un p -gon régulière est constructible à la règle, compas et un trisectrice angle.

Origami

Le théorie mathématique de l'origami est plus puissant que la boussole et de la construction de staightedge. Se plie satisfaire les axiomes Huzita-Hatori peut construire exactement le même ensemble de points que les constructions prolongées aide d'une boussole et d'une règle marquée. Donc origami peut aussi être utilisé pour résoudre des équations cubiques (et donc des équations du quatrième degré), et donc de résoudre deux problèmes classiques.

Le champ d'extension

En termes abstraits, l'utilisation de ces outils plus puissants de neusis soit en utilisant une règle remarquable ou les constructions de l'origami se étend le domaine de la numéros constructibles à un plus grand sous-champ des nombres complexes, qui contient non seulement la racine carrée, mais aussi la cube racines, de chaque élément. Les formules arithmétiques pour les points constructibles décrites ci-dessus ont des analogies dans ce domaine plus vaste, permettant formules qui comprennent des racines cubiques ainsi. L'extension du champ généré par ne importe quel point constructible supplémentaire dans ce domaine plus grande est de degré un multiple d'une puissance de deux et une puissance de trois, et peut être divisé en une tour d'extensions de degré 2 et 3.

Le calcul de chiffres binaires

En 1998, Simon Plouffe a donné une règle et au compas algorithme qui peut être utilisé pour calculer chiffres binaires de certains numéros. L'algorithme consiste essentiellement le doublement répétée d'un angle et devient physiquement impossible après environ 20 chiffres binaires.