Nombre ordinal

Représentation des nombres ordinaux jusqu'à ^ω ω. Chaque tour de la spirale représente une puissance de ω

En théorie des ensembles , un nombre ordinal, ou tout simplement ordinale, ce est le type d'un ordre ensemble bien ordonné. Ordinaux sont une extension des nombres naturels différents de nombres entiers et de cardinaux . Comme d'autres types de numéros, ordinaux peuvent être ajoutés, multipliés et exponentielles. Les ordinaux finis (et les cardinaux finis) sont les nombres naturels: 0, 1, 2, ..., puisque toutes les deux ordres totaux d'un ensemble fini sont commander isomorphe. L'ordinal infini est moins ω qui est identifié avec le nombre cardinal . Au-delà de ordinaux cependant ω (le cas transfinite) établir une distinction plus fine que les cardinaux en raison de leur information d'ordre. Considérant qu'il ne est qu'un cardinal infini dénombrable, à savoir lui-même, il ya de nombreux indénombrablement ordinaux infini dénombrable, à savoir ω, ω + 1, ω + 2, ..., ω · 2, ω · 2 + 1, ..., ω ^2, ..., ω ^3, ..., ^ω ω, ..., ^ω ω ω, ..., ε _0, .... Voici addition et la multiplication ne sont pas commutative: en particulier 1 + ω ω est plutôt que ω + 1, tandis que 2 · ω ω est plutôt que ω · 2. L'ensemble des ordinaux dénombrables constitue le premier ordinal dénombrable ω ₁ qui est identifié avec le cardinal (À côté cardinal après 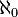). Cardinaux bien ordonnés sont identifiés avec leur ordinaux initiales, à savoir le plus petit ordinal de cette cardinalité. Le cardinal d'un ordinal définit une association plusieurs à un de ordinaux à cardinaux.

Ordinaux ont été introduites par Georg Cantor en 1897 pour accueillir séquences infinies et de classer des ensembles avec certains types de commander structures sur eux.

En général, chaque α ordinal est le type de l'ensemble des ordinaux strictement inférieure à se α de commande. Cette propriété permet tout ordinal d'être représenté comme l'ensemble de tous les ordinaux moins que lui. Ordinaux peuvent être classés comme suit: zéro, ordinaux successeurs, et de limiter les ordinaux (de divers cofinalities). Compte tenu de la classe des ordinaux, on peut identifier le membre de α-ème de cette classe, soit un indice de boîte (chiffre) eux. Une classe est fermée et illimitée si sa fonction d'indexation est continue et ne se arrête jamais. Le Cantor forme normale représente de manière unique chaque ordinale comme une somme finie des pouvoirs ordinales de ω. Cependant, cela ne peut pas constituer la base d'une notation ordinale universelle en raison de ces représentations auto-référentielles que 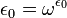. Ordinaux plus en plus grandes peuvent être définis, mais ils deviennent de plus en plus difficile à décrire. Ne importe quel nombre ordinal peut être faite dans un espace topologique en la dotant de la commander topologie; cette topologie est discrète si et seulement si l'ordinal est un cardinal comptable, ce est à dire au plus ω. Un sous-ensemble de ω + 1 est ouvert dans l'ordre topologie si et seulement si il est soit cofini ou il ne contient pas en tant qu'élément ω.

Ordinaux étendent les nombres naturels

Un nombre naturel (qui, dans ce contexte, comprend le nombre 0 ) peut être utilisé à deux fins: pour décrire la taille d'une fixer, ou pour décrire la position d'un élément dans une séquence. Lorsque restreinte aux ensembles finis ces deux concepts coïncident; il ya un seul moyen de mettre un ensemble fini en une séquence linéaire, à isomorphisme. Lorsque vous traitez avec des ensembles infinis on doit faire la distinction entre la notion de taille, ce qui conduit à un nombre de cardinaux , et la notion de position, qui est généralisée par les nombres ordinaux décrites ici. Ce est parce que, tandis que tout ensemble a une seule taille (sa cardinalité), il ya beaucoup de bons ordres non isomorphes de tout ensemble infini, comme expliqué ci-dessous.

Considérant que la notion de nombre cardinal est associé à un ensemble sans structure particulière sur elle, les ordinaux sont intimement liés à la nature particulière des ensembles qui sont appelés bien-commandés (si intimement liés, en fait, que certains mathématiciens ne font aucune distinction entre les deux concepts). Un ensemble bien ordonné est un ensemble totalement ordonné (donné aucun deux éléments on définit un petit et un plus grand de manière cohérente) dans lequel il ne est pas infinie suite décroissante (cependant, il peut y avoir des séquences croissantes infinies); équivalente, chaque sous-ensemble non vide de l'ensemble a un plus petit élément. Ordinaux peuvent être utilisés pour marquer les éléments d'un ensemble bien ordonné donnée (le plus petit élément étant marqué 0, celle d'après une, la suivante 2 ", et ainsi de suite") et de mesurer la «longueur» de l'ensemble fixé par le moins ordinale qui ne est pas une étiquette pour un élément de l'ensemble. Cette «longueur» se appelle le type de l'ensemble de la commande.

Toute ordinal est défini par l'ensemble des ordinaux qui le précèdent: en fait, la définition la plus commune des ordinaux identifie chaque ordinale comme l'ensemble des ordinaux qui le précèdent. Par exemple, l'ordinal 42 est le type des ordinaux inférieure à ce qu'elle, à savoir l'ordre, les ordinaux de 0 (le plus petit de tous les ordinaux) à 41 (le prédécesseur immédiat de 42), et il est généralement identifié comme l'ensemble {0 , 1,2, ..., 41}. Inversement, tout ensemble d'ordinaux qui est vers le bas fermé ce qui signifie que toute ordinale moins un ordinal dans le jeu est également dans le set-est (ou peut être identifié avec) un ordinal.

Jusqu'à présent, nous avons mentionné seulement ordinaux finis, qui sont les nombres naturels. Mais il ya des infinis ainsi: le plus petit ordinal infini est ω, qui est le type des nombres naturels (ordinaux finis) et qui peut même être identifiés à l'ensemble des nombres naturels (en effet l'ordre, l'ensemble des nombres naturels est bien -ordered, comme ce est un ensemble d'ordinaux et car il est à la baisse fermé il peut être identifié avec l'ordinal qui lui est associé, ce qui est exactement la façon dont nous définissons ω).

Un "allumette" représentation graphique de la ω² ordinale. Chaque bâton correspond à un ordinal de la forme ω · m + n où m et n sont des nombres naturels.

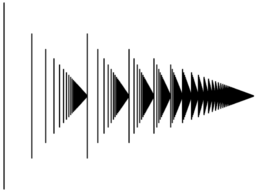
Peut-être une intuition claire des ordinaux peut être formé par l'examen d'un premier nombre d'entre eux: comme mentionné ci-dessus, elles débutent par des nombres naturels, 0, 1, 2, 3, 4, 5, ... Une fois que tous les nombres naturels entre le premier ordinal infini , ω, et après cela venir ω + 1, + 2 ω, ω + 3, et ainsi de suite. (Exactement ce que des moyens d'addition seront définies plus tard. Il suffit de les considérer comme des noms) Après tout cela se ω · 2 (qui est ω + ω), ω · 2 + 1, ω · 2 + 2, et ainsi de suite, alors ω · 3, puis plus tard ω · 4. Maintenant l'ensemble des ordinaux que nous formons de cette manière (l'ω · m + n, où m et n sont des nombres naturels) doit lui-même avoir un ordinal qui lui est associé: et ce est ω ^2. Plus loin, il y aura ω ^3, puis ω ^4, et ainsi de suite, et ^ω ω, alors ω ^ω², et beaucoup plus tard sur ε ₀ ( epsilon zéro) (pour donner quelques exemples de relativement petite dénombrable-ordinaux). Nous pouvons continuer de cette manière indéfiniment loin («indéfiniment loin» est exactement ce ordinaux sont bons: en gros à chaque fois on dit »et ainsi de suite" lors de l'énumération ordinaux, il définit un ordinal plus grand). Le plus petit ordinal indénombrable est l'ensemble de tous les ordinaux dénombrables, exprimée en ω _1.

Définitions

Ensembles bien ordonnés

Un ensemble bien ordonné est un ensemble ordonné dans lequel chaque sous-ensemble non vide a un élément moins: ce est l'équivalent (au moins en présence de la axiome du choix dépendant) juste dire que le jeu est totalement ordonné et il n'y a pas de suite décroissante infini, quelque chose qui est peut-être plus facile à visualiser. Dans la pratique, l'importance du bien-commande est justifiée par la possibilité d'appliquer récurrence transfinie, qui dit, en substance, que les biens qui passe sur des prédécesseurs d'un élément à cet élément lui-même doit être vrai de tous les éléments (de l'ensemble bien ordonnée donnée). Si les états d'un calcul (programme d'ordinateur ou jeu) peuvent être bien ordonné de telle sorte que chaque étape est suivie d'une étape "inférieur", alors vous pouvez être sûr que le calcul prendra fin.

Maintenant, nous ne voulons pas faire la distinction entre deux ensembles bien ordonnés si elles ne diffèrent que par la «labellisation de leurs éléments", ou plus formellement: si nous pouvons apparier les éléments de la première série avec les éléments de la deuxième série tels que, si un élément est plus petit que l'autre dans la première série, alors le partenaire du premier élément est plus petit que le partenaire du second élément dans le deuxième ensemble, et vice versa. Une telle correspondance un-à-un est appelé un Afin isomorphisme et les deux ensembles bien ordonnés sont dits ordre isomorphe, ou similaire (évidemment ce est une relation d'équivalence ). Sous réserve qu'il existe un isomorphisme d'ordre entre deux ensembles bien ordonnés, l'ordre isomorphisme est unique: ce qui rend tout à fait justifiable d'examiner les ensembles comme essentiellement identiques, et de chercher un représentant "canonique" du type d'isomorphisme (de classe). Ce est exactement ce que les ordinaux fournissent, et il fournit également un étiquetage canonique des éléments de tout ensemble bien ordonné.

Nous souhaitons donc essentiellement à définir un ordinal comme une classe d'isomorphisme d'ensembles bien ordonnés: qui est, comme un classe d'équivalence pour la relation d'équivalence d '«être-pour isomorphe". Il existe une difficulté technique, cependant, dans le fait que la classe d'équivalence est trop grande pour un ensemble de la manière habituelle Zermelo-Fraenkel (ZF) formalisation de la théorie des ensembles. Mais ce ne est pas une difficulté sérieuse. Nous dirons que l'ordinal est le type de tout ensemble dans la classe de commande.

Définition d'un ordinal comme une classe d'équivalence

La définition originale du nombre ordinal, trouve par exemple dans Principia Mathematica, définit le type d'un bon ordre afin que l'ensemble de tous les bien-ordres similaire (ordre isomorphe) pour que le bien-commande: en d'autres termes, un nombre ordinal est véritablement une classe d'équivalence des ensembles bien ordonnés. Cette définition doit être abandonné en ZF et des systèmes connexes de la théorie des ensembles axiomatique parce que ces classes d'équivalence sont trop grosses pour former un ensemble. Toutefois, cette définition ne peut toujours être utilisé dans la théorie de type et dans la théorie des ensembles de Quine Nouvelles fondations et des systèmes connexes (où il offre une solution de rechange assez surprenant de la Paradoxe de la plus grande ordinale Burali-Forti).

Définition de Von Neumann des ordinaux

Plutôt que de définir un ordinal comme une classe d'équivalence des ensembles bien ordonnés, nous allons définir comme un ensemble bien ordonné particulière qui (canoniquement) représente la classe. Ainsi, un nombre ordinal sera un ensemble bien ordonné; et chaque ensemble bien ordonné sera pour-isomorphe à exactement un nombre ordinal.

La définition standard, proposée par John von Neumann , est: chaque ordinal est l'ensemble bien ordonné de toutes les petites ordinaux. En symboles, λ = [0, λ). Formellement:

Un ensemble S est un ordinal si et seulement si S est strictement bien ordonné à l'égard de l'adhésion et fixer chaque élément de S est aussi un sous-ensemble de S.

On notera que les nombres naturels sont des ordinaux par cette définition. Par exemple, la figure 2 est un élément du 4 = {0, 1, 2, 3}, et la figure 2 est égale à {0, 1} et il est donc un sous-ensemble {0, 1, 2, 3}.

On peut montrer par récurrence transfinie que chaque ensemble bien ordonné est pour-isomorphe à exactement un de ces ordinaux, qui est, il est une ordonnance de conservation fonction bijective entre eux.

En outre, les éléments de chaque ordinal ordinaux sont eux-mêmes. Chaque fois que vous avez deux ordinaux S et T, S est un élément de T si et seulement si S est un sous-ensemble de T. De plus, soit S est un élément de T, ou T est un élément de S, ou ils sont égaux. Ainsi, chaque ensemble de ordinaux est totalement ordonné. En outre, chaque ensemble d'ordinaux est bien ordonné. Ceci généralise le fait que chaque ensemble de nombres naturels est bien ordonné.

Par conséquent, tout ordinal S est un ensemble ayant comme éléments précisément les ordinaux plus petits que S. Par exemple, chaque ensemble de ordinaux a une supremum, l'ordinal obtenu en prenant l'union de tous les ordinaux dans l'ensemble. Cette union existe indépendamment de la taille de l'ensemble, par le axiome de l'union).

La classe de tous les ordinaux ne est pas un ensemble. Si ce était un jeu, on a pu démontrer que ce était un ordinal et donc un membre d'elle-même qui contredit son ordre strict par l'adhésion. Ceci est le Paradoxe Burali-Forti. La classe de tous les ordinaux est diversement appelé "Ord", "ON" ou "∞".

Un ordinal est finie si et seulement si l'ordre inverse est également bien ordonnée, ce qui est le cas si et seulement si chacun de ses sous-ensembles a une maximale.

Autres définitions

Il existe d'autres formulations modernes de la définition de ordinale. Par exemple, en supposant que le axiome de régularité, ce qui suit sont équivalentes pour un ensemble x:

• x est un ordinal,
• x est un ensemble transitif, et réglez l'adhésion est trichotomique sur x,
• x est un ensemble transitif totalement ordonné par inclusion ensembliste,
• x est un ensemble d'ensembles transitifs transitive.

Ces définitions peuvent pas être utilisés dans non bien-fondé des théories établies. Dans set théories avec urelements, il faut faire plus que ce que la définition exclut urelements d'apparaître dans ordinaux.

Séquence Transfinite

Si α est un ordinal limite et X est un ensemble, une séquence d'éléments de X-α indexées est une fonction de α à X. Ce concept, une séquence ou la séquence ordinale transfinite indexées, est une généralisation de la notion de séquence . Une séquence ordinaire correspond au cas α = ω.

Récurrence transfinie

Qu'est-ce que l'induction transfinie?

Récurrence transfinie détient dans toute ensemble bien ordonné, mais il est si important par rapport à ordinaux qu'il est utile de rappeler ici.

Toute propriété qui passe de l'ensemble des ordinaux plus petits qu'un α ordinal donné à lui-même α, est vrai de tous les ordinaux.

Ce est, si P (α) est vrai lorsque P (β) est vrai pour tous les β <α, alors P (α) est vrai pour tous α. Ou, plus concrètement: afin de prouver une propriété P pour tous les ordinaux α, on peut supposer qu'il est déjà connu pour toutes plus petites β <α.

Récursivité Transfinite

Transfinite induction peut être utilisé non seulement pour prouver des choses, mais aussi de les définir. Une telle définition est normalement dite par récurrence transfinie - la preuve que le résultat est bien défini utilise l'induction transfinie. Soit F un (classe) fonction F à définir sur les ordinaux. L'idée est maintenant que, dans la définition de F (α) pour un α ordinal quelconque, on peut supposer que F (β) est déjà définie pour tout β <α et de donner ainsi une formule F (α) en termes de ces F ( β). Il se ensuit par induction transfinie qu'il existe une et une seule fonction satisfaisant la formule de récurrence jusqu'à et y compris α.

Voici un exemple de définition par récurrence transfinie sur les ordinaux (plus sera donné plus loin): définir la fonction F en laissant F (α) le plus petit ordinal pas dans la classe {F (β) | β <α}, ce est- , la classe constituée de l'ensemble F (β) pour β <α. Cette définition suppose F (β) connu dans le processus même de la définition de F; ce cercle vicieux apparent est exactement ce que la définition par des permis de récurrence transfinis. En fait, F (0) est logique puisqu'il n'y a pas ordinale β <0, et la classe {F (β) | β <0} est vide. Donc F (0) est égale à 0 (le plus petit de tous ordinal). Maintenant que F (0) est connu, la définition appliquée à F (1) a un sens (ce est le plus petit ordinal pas dans la classe de singleton {F (0)} = {0}), et ainsi de suite (le, etc. est exactement l'induction transfinie). Il se avère que cet exemple ne est pas très excitant, car prouvablement F (α) = α pour tous les ordinaux α, qui peuvent être représentés, précisément, par induction transfinie.

Successeur et limites ordinaux

Toute ordinale non nul a l'élément minimal, zéro. Il peut ou peut ne pas être un élément maximum. Par exemple, 42 a et 41 maximale ω + ω a 6 + 5 maximales. D'autre part, ω ne possède un maximum puisqu'il n'y a pas plus grand nombre entier naturel. Si un ordinal α a un maximum, puis il est la prochaine ordinale après α, et il est appelé successeur ordinale, à savoir le successeur de α, α écrite + 1. Dans la définition de von Neumann d'ordinaux, le successeur de α est 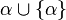étant donné que ses éléments sont ceux de α et α elle-même.

Un ordinal non nul qui ne est pas un successeur est appelé limiter ordinale. Une justification de ce terme est qu'un ordinal limite est en effet le limite dans un sens topologique de tous les petits ordinaux (sous la Afin topologie).

Quand 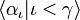est une séquence d'ordinale indexées, indexées par un γ limite et la séquence est en augmentation, ce est à dire 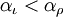chaque fois que 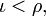nous définissons sa limite pour la borne supérieure de l'ensemble 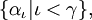ce est, le plus petit ordinal (elle existe toujours) plus grande que ne importe quel terme de la suite. En ce sens, un ordinal limite est la limite de tous les ordinaux plus petits (indexées par lui-même). Mettez plus directement, ce est la borne supérieure de l'ensemble des petites ordinaux.

Une autre façon de définir une limite ordinal est-à-dire que α est une limite ordinal si et seulement si:

Il est un ordinal moins de α et chaque fois que ζ est un ordinal moins de α, alors il existe un ordinal ξ telle que ζ <ξ <α.

Donc, dans l'ordre suivant:

0, 1, 2, ..., ω, ω + 1

ω est un ordinal limite, car pour tout ordinal (dans cet exemple, un nombre naturel), nous pouvons trouver un autre ordinale (nombre naturel) plus grande que lui, mais toujours moins de ω.

Ainsi, tout ordinal est soit zéro, soit un successeur (d'un prédécesseur bien défini), ou une limite. Cette distinction est importante, parce que beaucoup de définitions par récurrence transfinie comptent sur elle. Très souvent, lors de la définition d'une fonction F par induction transfinie sur tous les ordinaux, on définit F (0), et F (α + 1) en supposant F (α) est défini, puis, pour la limite ordinaux δ on définit F (δ) comme la limite de la F (β) pour tout β <δ (soit dans le sens des limites ordinales, comme nous venons de l'expliquer, ou pour quelque autre notion de limite si F ne prenez pas des valeurs ordinales). Ainsi, l'étape intéressante dans la définition est l'étape de successeur, pas la limite ordinaux. Ces fonctions (en particulier pour F non décroissante et en prenant des valeurs ordinales) sont appelés continue. Nous verrons que l'addition ordinale, la multiplication et exponentiation sont continues comme des fonctions de leur second argument.

les classes d'indexation de ordinaux

Nous avons mentionné que tout ensemble bien ordonné est similaire (ordre isomorphe) à un numéro d'ordre unique, , Ou, en d'autres termes, que ses éléments peuvent être indexés à accroître la mode par les ordinaux moins de . Cela se applique, en particulier, à un ensemble d'ordinaux: tout ensemble d'ordinaux est naturellement indexé par les ordinaux moins que certains . Il en est de même, avec une légère modification, pour les classes de ordinaux (une collection des ordinaux, peut-être trop grande pour former un ensemble, défini par une propriété): toute catégorie de ordinaux peut être indexé par ordinaux (et, lorsque la classe est sans limite dans la classe de tous les ordinaux, cela met en classe-bijection avec la classe de tous les ordinaux). Ainsi, nous pouvons parler librement de la 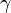ième élément de la classe (avec la convention selon laquelle le "0-ième» est le plus petit, le "1-ième" est la plus petite suivante, et ainsi de suite). Formellement, la définition est par induction transfinie: la 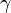-ième élément de la classe est définie (à condition qu'il ait déjà été défini pour tous 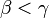), Selon le plus petit élément supérieur au 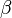-ième élément pour tous .

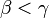Nous pouvons appliquer cette, par exemple, à la classe des ordinaux limites: la 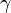ordinale ième qui est soit une limite ou le zéro 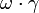(Voir arithmétique ordinale pour la définition de la multiplication de nombres ordinaux). De même, nous pouvons considérer ordinaux indécomposables additive (ce qui signifie un ordinal non nul qui ne est pas la somme de deux ordinaux strictement plus petits): les 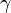ième ordinal indécomposable additive est indexé comme 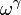. La technique de classes d'indexation des ordinaux est souvent utile dans le contexte de points fixes: par exemple, la 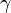ordinale ième tel que 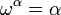est écrit 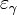. On les appelle les " numéros epsilon ".

Ensembles et les classes non bornés fermés

Une classe des ordinaux est dit être sans limite, ou cofinal, quand donné toute ordinale, il ya toujours un élément de la classe supérieure à ce qu'elle (alors la classe doit être une classe appropriée, ce est à dire, il ne peut pas être un ensemble). Il est dit fermé lorsque la limite d'une séquence d'ordinaux dans la classe est à nouveau dans la classe: ou, de façon équivalente, lorsque la fonction d'indexation (classe) 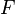est continu en ce sens que, pour 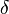ordinal limite, (Le 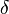ordinale ième dans la classe) est la limite de tous 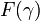pour 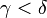; ce est également le même que celui d'être fermé, dans le sens topologique, pour la Afin topologie (pour éviter de parler de la topologie sur les classes appropriées, on peut exiger que l'intersection de la classe avec toute donnée ordinale est fermé pour la topologie de l'ordre sur ce ordinale, ce est encore l'équivalent).

Une importance particulière sont les classes de ordinaux qui sont fermé et sans limite, parfois appelé clubs. Par exemple, la classe de tous les ordinaux limites est fermé et sans limite: cela se traduit par le fait qu'il ya toujours un ordinal limite supérieure à un ordinal donné, et que la limite de limites ordinaux est un ordinal limite (un fait heureux si la terminologie est à aucun sens du tout!). La classe des ordinaux indécomposables additive, ou la catégorie de 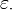ordinaux, ou la classe des cardinaux , sont tous fermés illimitée; l'ensemble des réguliers cardinaux, cependant, ne est pas borné mais pas fermé, et tout ensemble fini de ordinaux est fermée mais pas illimitée.

Une classe est stationnaire si elle a une intersection non vide avec chaque classe illimitée fermé. Tous les super-classes de classes non bornés fermés sont des classes fixes et stationnaires sont sans limite, mais il ya des classes fixes qui ne sont pas fermés et il ya des classes fixes qui ne ont pas sous-classe illimitée fermé (comme la classe de tous les ordinaux limites avec cofinalité dénombrable). Depuis l'intersection de deux classes illimitées fermés est fermé et sans limite, l'intersection d'une classe et une classe fixe illimitée fermé est stationnaire. Mais l'intersection de deux classes stationnaires peut être vide, par exemple la classe des ordinaux avec cofinalité ω avec la classe des ordinaux avec cofinalité innombrables.

Plutôt que de la formulation de ces définitions pour les classes d'ordinaux (propres), nous pouvons les formuler pour les ensembles d'ordinaux dessous d'un ordinal donné : Un sous-ensemble d'un ordinal limite est dit être sans limite (ou cofinal) sous à condition que tout ordinal moins est moins que certains ordinale dans l'ensemble. Plus généralement, nous pouvons appeler un sous-ensemble de tout ordinale cofinal dans à condition tout ordinal moins de est inférieure ou égale à un certain ordinal de l'ensemble. Le sous-ensemble est dit être fermé en vertu à condition qu'il soit fermé pour la topologie de l'ordre dans , Ce est à dire une limite d'ordinaux dans l'ensemble est soit dans le jeu ou égal à lui-même.

Arithmétique des ordinaux

Il ya trois opérations habituelles sur ordinaux: addition, multiplication, et (ordinale) exponentiation. Chacun peut être défini dans essentiellement deux façons différentes: soit par la construction d'un ensemble explicite bien ordonnée qui représente l'opération ou en utilisant la récursivité transfinite. Cantor forme normale fournit un moyen normalisé d'écrire ordinaux. Les soi-disant opérations arithmétiques "naturels" conservent commutativité au détriment de la continuité.

Ordinaux et cardinaux

Ordinal initial d'un cardinal

Chaque ordinale a un associé cardinal , son cardinal, obtenu en oubliant simplement l'ordre. Tout ensemble bien ordonné que ordinale ayant comme type de commande a le même cardinal. Le plus petit ordinal ayant un cardinal donné que son cardinal est appelé l'ordinal initial de ce cardinal. Chaque ordinale finis (nombre naturel) est initiale, mais la plupart des ordinaux infinis ne sont pas initial. Le axiome du choix est équivalent à la déclaration que tout ensemble peut être bien ordonné, ce est à dire que chaque cardinal a un ordinal initial. Dans ce cas, il est de tradition d'identifier le nombre cardinal avec son ordinal initial, et nous dire que l'ordinal initial est un cardinal.

L'infini ordinal initial α-e est écrit 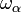. Son cardinal est écrit 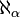. Par exemple, la cardinalité de ω = ω ₀ est 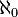, Qui est aussi le cardinal de ω² ou ε ₀ (tous sont ordinaux dénombrables). Donc (en supposant que l'axiome du choix), nous identifions avec ω 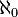, Sauf que la notation 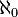est utilisé lors de l'écriture cardinaux et ordinaux ω lors de l'écriture (ce est important car 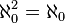alors que 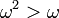). Aussi, 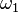est le plus petit ordinal indénombrable (pour voir qu'il existe, considérer l'ensemble des classes d'équivalence de bons ordres des nombres naturels: chaque bon ordre tels définit un ordinal dénombrable, et 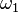est le type de ce jeu de commande), 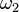est le plus petit ordinal dont le cardinal est supérieure à 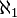Et ainsi de suite, et 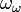est la limite de la 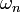pour les numéros naturel n (aucune limite de cardinaux est un cardinal, si cette limite est en effet le premier cardinal, après tout le ).

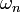Voir également Von Neumann Affectation de cardinal.

Cofinalité

Le cofinalité d'un ordinal est le plus petit ordinal 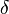qui est le type d'une commande de sous-ensemble de cofinal . Notez qu'un certain nombre d'auteurs définir confinality ou l'utiliser seulement pour ordinaux limites. Le cofinalité d'un ensemble d'ordinaux ou tout autre ensemble bien ordonné est la cofinalité du type de ce jeu de commande.

Ainsi, pour un ordinal limite, il existe un 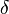-indexed croissante strictement séquence avec limite . Par exemple, le cofinalité de ω² est ω, parce que la séquence ω · m (où m est compris dans les nombres naturels) tend à ω²; mais, plus généralement, tout ordinal limite dénombrable a cofinalité ω. Un ordinal limite incalculable peut avoir soit cofinalité ω comme le fait 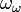ou un cofinalité innombrables.

Le cofinalité de 0 est 0. Et le cofinalité de tout ordinal successeur est 1. Le cofinalité de tout ordinal limite est au moins .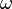

Un ordinal qui est égale à sa cofinalité est appelé régulier et il est toujours un ordinal initial. Toute limite des ordinaux réguliers est une limite de ordinaux initiales et est également initiale, même si elle ne est pas régulière, qui ne est généralement pas ainsi. Si l'axiome du choix, puis 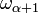est normal pour chaque α. Dans ce cas, les ordinaux 0, 1, 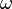, 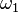Et 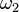sont régulières, tandis que 2, 3, 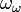Et _ω ω _{· 2} sont ordinaux initiales qui ne sont pas régulières.

Le cofinalité selon l'une quelconque ordinal α est un ordinal régulier, ce est à dire la cofinalité du cofinalité de α est la même que la cofinalité de α. Donc, l'opération de cofinalité est idempotent.

Certains «grands» ordinaux dénombrables

Nous avons déjà mentionné (voir Cantor de forme normale), le ε ordinale _0, ce qui est le plus petit satisfaisant à l'équation 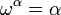, De sorte que ce est la limite de la séquence 0, 1, 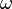, , 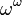, 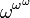Etc. Beaucoup ordinaux peuvent être définis d'une manière telle que des points fixes de certaines fonctions ordinales (le ordinal tel que -ième 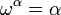est appelé 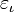, Alors nous pourrions continuer à essayer de trouver le ordinal tel que -ième 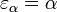», Et ainsi de suite», mais toute la subtilité réside dans le "et ainsi de suite"). Nous pouvons essayer de le faire systématiquement, mais ne importe quel système est utilisé pour définir et construire ordinaux, il ya toujours un ordinal qui se trouve juste au-dessus de tous les ordinaux construits par le système. Peut-être un système de construction ordinal le plus important qui limite de cette manière est le Church- Kleene ordinale, 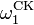(Malgré la dans le nom, cette ordinale est dénombrable), qui est le plus petit ordinal qui ne peuvent en aucune façon être représenté par un fonction calculable (ce qui peut être fait rigoureuse, bien sûr). Considérablement grandes ordinaux peuvent être définis ci-dessous 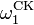Cependant, qui mesurent la "résistance à la preuve théorique" de certaines systèmes formels (par exemple, 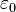mesure de la force Arithmétique de Peano). Grandes ordinaux peuvent également être définis ci-dessus l'ordinal Eglise-Kleene, qui sont d'intérêt dans diverses parties de la logique.

Topologie et ordinaux

Toute ordinal peut être transformé en un espace topologique de façon naturelle en la dotant de la Afin topologie. Voir la section Topologie et ordinaux de la "Topologie de l'ordre" article.

La baisse ensembles fermés d'ordinaux

Un ensemble est la baisse fermées si rien de moins que d'un élément de l'ensemble est également dans le set. Si un ensemble d'ordinaux est à la baisse fermé, alors ce jeu est un ordinal-ordinal le moins pas dans le jeu.

Exemples:

• L'ensemble des ordinaux de moins de 3 est 3 = {0, 1, 2}, le plus petit ordinal pas inférieur à 3.
• L'ensemble des ordinaux finis est infini, le plus petit ordinal infini: ω.
• L'ensemble des ordinaux dénombrables est dénombrable, le plus petit ordinal indénombrable: ω _1.