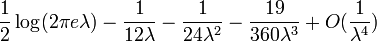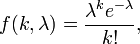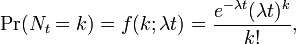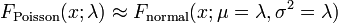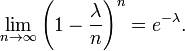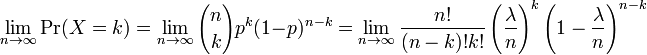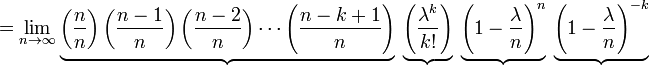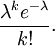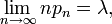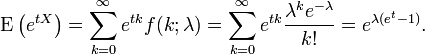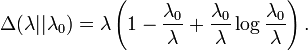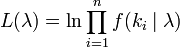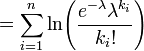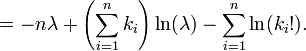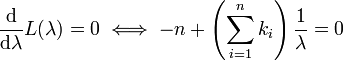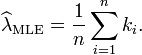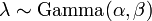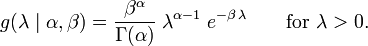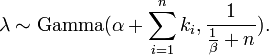Distribution de Poisson
À propos de ce écoles sélection Wikipedia
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.
Fonction de masse 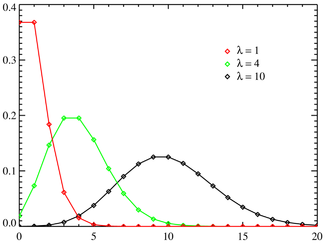 L'axe horizontal est l'indice k. La fonction est définie seulement à des valeurs entières de k. Les lignes de connexion ne sont que des guides pour l'œil et ne indiquent pas la continuité. | |
Fonction de distribution cumulative 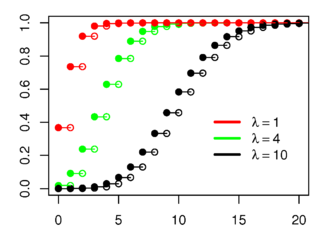 L'axe horizontal est l'indice k. | |
| Paramètres | 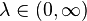 |
|---|---|
| Soutien | 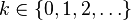 |
| PMF | 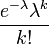 |
| CDF | 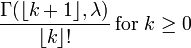 (Où |
| Signifier | 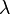 |
| Médiane | 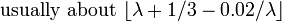 |
| Mode | 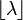 et et 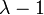 si si 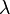 est un nombre entier est un nombre entier |
| Variance | 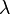 |
| Asymétrie | 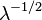 |
| Ex. aplatissement | 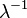 |
| Entropy | ![\ Lambda [1 \ -! \ \ Ln (\ lambda)]! \ + \ E ^ {- \ lambda} \ sum_ {k = 0} ^ \ infty \ frac {\ lambda ^ k \ ln (k! )} {k!}](../../images/97/9713.png) (Pour les grands |
| MGF | 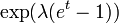 |
| FC | 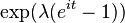 |
Dans la théorie des probabilités et des statistiques , la distribution de Poisson est une distribution de probabilité discrète qui exprime la probabilité d'un certain nombre d'événements qui se produisent dans une période de temps déterminée si ces événements se produisent avec un taux moyen connu et indépendamment du temps écoulé depuis le dernier événement. La distribution de Poisson peut également être utilisé pour le nombre d'événements dans d'autres intervalles déterminés tels que la distance, surface ou de volume.
La distribution a été découvert par Siméon-Denis Poisson ( 1781 - 1840 ) et publiée, avec sa théorie de la probabilité, en 1838 dans son ouvrage Recherches sur la Probabilité des Jugements en matières criminelles et matière civile («La recherche sur la probabilité des décisions en matière civile et pénale») . Les travaux ont porté sur certaines variables aléatoires N qui comptent, entre autres, un certain nombre d'occurrences discrètes (parfois appelé «arrivées») qui ont lieu au cours d'un temps -interval de longueur donnée. Si le nombre d'occurrences prévu dans cet intervalle est λ, alors la probabilité que sont exactement les occurrences k (k étant un non-négatif entier , k = 0, 1, 2, ...) est égal à
où
- e est la base du logarithme naturel (e = 2,71828 ...)
- k est le nombre d'occurrences d'un événement - dont la probabilité est donnée par la fonction
- k! est la factorielle de k
- λ est positif un nombre réel égal au nombre attendu d'événements qui se produisent pendant l'intervalle donné. Par exemple, si les événements se produisent en moyenne toutes les 4 minutes, et vous êtes intéressé par le nombre d'événements survenus dans un intervalle de 10 minutes, vous pouvez utiliser comme modèle une distribution de Poisson avec λ = 10/4 = 2,5.
En fonction de k, ce est le Fonction de masse. La distribution de Poisson peut être calculée comme un cas limite de la loi binomiale .
La distribution de Poisson peut être appliquée à des systèmes avec un grand nombre d'événements possibles, dont chacun est rare. Un exemple classique est la désintégration nucléaire d'atomes.
La distribution de Poisson est parfois appelé un de Poisson, analogue à la gaussienne terme de Gauss ou distribution normale .
bruit de Poisson et la caractérisation de petites occurrences
Le paramètre λ est pas seulement le moyen pour nombre d'occurrences 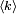 , Mais aussi sa variance
, Mais aussi sa variance 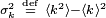 (Voir le tableau). Ainsi, le nombre d'occurrences observées fluctue autour de sa moyenne λ avec un écart-type
(Voir le tableau). Ainsi, le nombre d'occurrences observées fluctue autour de sa moyenne λ avec un écart-type 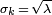 . Ces fluctuations sont désignés par le bruit de Poisson ou (en particulier dans l'électronique) que bruit de grenaille.
. Ces fluctuations sont désignés par le bruit de Poisson ou (en particulier dans l'électronique) que bruit de grenaille.
La corrélation de l'écart moyen et l'écart dans le comptage, les événements discrets indépendants est utile scientifiquement. En surveillant la façon dont les fluctuations varient avec le signal de moyenne, on peut estimer la contribution d'un seul événement, même si cette contribution ne est trop petit pour être détecté directement. Par exemple, la charge e sur un électron peut être estimé en corrélant l'amplitude d'un courant électrique avec son bruit de grenaille. Si N électrons passent un point dans un temps donné t en moyenne, la moyenne courant est I = fr / t; puisque les fluctuations actuelles devraient être de l'ordre 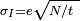 (Ce est à dire l' écart du processus de Poisson), la charge e peut être estimée à partir du rapport
(Ce est à dire l' écart du processus de Poisson), la charge e peut être estimée à partir du rapport 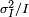 . Un exemple courant est le grain qui apparaît comme des photos sont agrandies; le grain est en raison des fluctuations de Poisson du nombre de réduction argent céréales, de ne pas les grains individuels eux-mêmes. En corrélant le grain avec le degré de l'élargissement, on peut estimer la contribution d'un grain individuel (qui est par ailleurs trop petit pour être vu nu). De nombreuses autres applications moléculaires de Poisson bruit ont été développés, par exemple, l'estimation de la densité en nombre de des molécules de récepteur dans un membrane cellulaire.
. Un exemple courant est le grain qui apparaît comme des photos sont agrandies; le grain est en raison des fluctuations de Poisson du nombre de réduction argent céréales, de ne pas les grains individuels eux-mêmes. En corrélant le grain avec le degré de l'élargissement, on peut estimer la contribution d'un grain individuel (qui est par ailleurs trop petit pour être vu nu). De nombreuses autres applications moléculaires de Poisson bruit ont été développés, par exemple, l'estimation de la densité en nombre de des molécules de récepteur dans un membrane cellulaire.
Distributions connexes
- Si
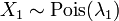 et
et 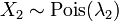 alors la différence
alors la différence 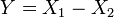 suit une Loi de Skellam.
suit une Loi de Skellam. - Si
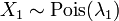 et
et 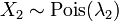 sont indépendants, et
sont indépendants, et 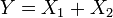 , Alors la distribution de
, Alors la distribution de 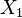 sur conditionnelle
sur conditionnelle 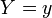 est un binôme . Plus précisément,
est un binôme . Plus précisément, 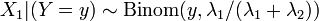 . Plus généralement, si X 1, X 2, ..., X n sont des variables aléatoires de Poisson avec des paramètres λ 1, λ 2, ..., λ n, puis
. Plus généralement, si X 1, X 2, ..., X n sont des variables aléatoires de Poisson avec des paramètres λ 1, λ 2, ..., λ n, puis 
- La distribution de Poisson peut être dérivé comme un cas limite de la distribution binomiale en tant que le nombre d'essais tend vers l'infini et le nombre prévu de succès reste fixe. Par conséquent, il peut être utilisé comme une approximation de la distribution binomiale si n est suffisamment grand et p est suffisamment faible. Il existe une règle de base indiquant que la distribution de Poisson est une bonne approximation de la distribution binomiale si n vaut au moins 20 et p est inférieur ou égal à 0,05. Selon cette règle, le rapprochement est excellent si n ≥ 100 et ≤ 10 np.
- Pour suffisamment grandes valeurs de λ, (par exemple λ> 1 000), la distribution normale avec la moyenne λ, λ et la variance, est une excellente approximation de la distribution de Poisson. Si λ est supérieur à environ 10, puis la distribution normale est une bonne approximation si une appropriée correction de continuité est réalisé, ce est à dire P (X ≤ x), où (minuscules) x est un nombre entier non-négatif, est remplacé par P (X ≤ x + 0,5).
- Si le nombre d'arrivées dans un temps donné suite à la distribution de Poisson, de moyenne =
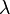 , Alors les longueurs des temps inter-arrivées suivent la Distribution exponentielle , avec un taux
, Alors les longueurs des temps inter-arrivées suivent la Distribution exponentielle , avec un taux 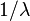 .
.
Occurrence
La distribution de Poisson se pose dans le cadre de Processus de Poisson. Elle se applique aux divers phénomènes de nature discrète (ce est à dire ceux qui peuvent se produire à 0, 1, 2, 3, ... fois pendant une période de temps donnée ou dans une zone donnée) chaque fois que la probabilité de ce phénomène se produit est constant dans temps ou espace. Des exemples d'événements qui peuvent être modélisées comme une distribution de Poisson comprennent:
- Le nombre de voitures qui passent à travers un certain point sur une route (à une distance suffisante de feux de circulation) pendant une période de temps donnée.
- Le nombre de fautes d'orthographe lors de la frappe on fait une seule page.
- Le nombre de coups de téléphone à un centre d'appel par minute.
- Le nombre de fois qu'un serveur Web est accessible par minute.
- Le nombre de Roadkill (animaux tués) trouvé par unité de longueur de la route.
- Le nombre de des mutations dans un segment donné de l'ADN après une certaine quantité de rayonnement.
- Le nombre de instables noyaux decayó que dans une période de temps donnée dans un morceau de substance radioactive. La radioactivité de la substance se affaiblissent avec le temps, si l'intervalle de temps total utilisé dans le modèle doit être nettement inférieure à la durée de vie de la substance signifie.
- Le nombre d'arbres de pin par unité de surface de forêt mixte.
- Le nombre de étoiles dans un volume donné de l'espace.
- Le nombre de soldats tués par des coups de pied de chevaux chaque année dans chaque corps de la Cavalerie prussienne. Cet exemple a été rendu célèbre par un livre de Ladislaus Bortkiewicz Josephovich ( 1868 - 1931 ).
- La distribution des cellules des récepteurs visuels de la rétine de la humaine oeil .
- Le nombre d'ampoules qui grillent en un certain laps de temps.
- Le nombre de virus qui peuvent infecter une cellule en culture cellulaire.
- Le nombre de cellules souches hématopoïétiques dans un échantillon de cellules de moelle osseuse non fractionnée.
- Le nombre d'inventions d'un inventeur cours de leur carrière.
- Le nombre de particules qui "scatter" hors d'une cible dans une expérience de physique nucléaire ou élevé.
[Note: les intervalles entre les événements successifs de Poisson sont-liés réciproquement, la suite de la Distribution exponentielle . Par exemple, la durée de vie d'une ampoule, ou le temps d'attente entre les bus.]
Comment cette distribution se pose? - La loi d'événements rares
Dans plusieurs de l'exemple des exemples-ci-dessus, le nombre de mutations dans une séquence donnée d'ADN les événements étant comptés sont en fait les résultats des essais discrets, et serait plus précisément être modélisée en utilisant la loi binomiale . Cependant, la distribution binomiale de paramètres n et λ / n, ce est à dire, la distribution de probabilité du nombre de succès en n essais, avec une probabilité λ / n de réussite à chaque essai, se rapproche de la distribution de Poisson avec une valeur attendue λ que n tend vers l'infini . Cette limite est parfois connu comme la loi d'événements rares, bien que ce nom peut être trompeur parce que les événements dans un processus de Poisson ne sont pas nécessairement rares (le nombre d'appels téléphoniques à un standard très occupé en une heure suit une distribution de Poisson, mais ces événements ne serait pas considérée comme rare). Il fournit un moyen par lequel, rapprochant les variables aléatoires en utilisant la distribution de Poisson, plutôt que la distribution binomiale plus encombrant.
Voici les détails. Tout d'abord, rappeler de calcul que
Soit p = λ / n. Ensuite, nous avons
Comme n tend vers ∞, l'expression sur le premier underbrace approche 1; le second reste constant depuis "n" ne apparaît pas dans du tout; la troisième approche e -λ; et la quatrième expression approche 1.
Par conséquent, la limite est
Plus généralement, chaque fois une séquence de variables aléatoires binomiale de paramètres n et p n est telle que
la séquence converge en loi vers une variable aléatoire de Poisson de moyenne λ (voir, par exemple, la loi d'événements rares).
Propriétés
- Le valeur attendue d'une variable aléatoire de Poisson-distribuée est égale à λ et il en est de sa variance . La plus haute des moments de la distribution de Poisson sont Polynômes Touchard à λ, dont les coefficients ont une combinatoire sens. En fait, lorsque la valeur attendue de la distribution de Poisson est 1, alors La formule de Dobinski dit que le n-ième instant égal au nombre de partitions d'un ensemble de taille n.
- Le Mode d'une variable aléatoire de Poisson-distribué avec non entier λ est égal à
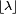 , Qui est le plus grand entier inférieur ou égal à λ. Ce est aussi écrit que étage (λ). Lorsque λ est un nombre entier positif, les modes sont λ et λ - 1.
, Qui est le plus grand entier inférieur ou égal à λ. Ce est aussi écrit que étage (λ). Lorsque λ est un nombre entier positif, les modes sont λ et λ - 1.
- Les sommes de variables aléatoires de Poisson distribués:
- Si
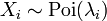 suivre une distribution de Poisson de paramètre
suivre une distribution de Poisson de paramètre 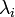 et
et 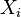 sont indépendante, puis
sont indépendante, puis 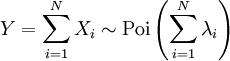 suit aussi une loi de Poisson dont le paramètre est la somme des paramètres de composants.
suit aussi une loi de Poisson dont le paramètre est la somme des paramètres de composants.
- Le Fonction génératrice des moments de la distribution de Poisson avec une valeur λ est attendue
- La totalité de la cumulants de la distribution de Poisson sont égales à la valeur λ attendu. La n-ième moment factoriel de la distribution de Poisson est λ n.
- Les distributions de Poisson sont infiniment divisible distributions de probabilité.
- La scène Kullback-Leibler entre Poi (λ 0) et Poi (λ) est donnée par
Génération Poisson-distribué variables aléatoires
Une façon simple de générer des numéros de Poisson-distribués au hasard est donnée par Knuth , voir les références ci-dessous.
algorithme poisson nombre aléatoire (Knuth):
INIT:
Soit L ← e -λ, k ← ← p 0 et 1.
faire:
k ← k + 1.
Générer uniforme nombre aléatoire u dans [0,1] et laisser p ← p × u.
tout p ≥ L.
retourner k - 1.
Bien que simple, la complexité est linéaire en λ. Il ya beaucoup d'autres algorithmes pour surmonter cela. Certains sont donnés dans Ahrens & Dieter, voir les références ci-dessous.
Estimation des paramètres
Maximum de vraisemblance
Étant donné un échantillon de n valeurs mesurées k i nous voulons estimer la valeur du paramètre λ de la population de Poisson à partir de laquelle l'échantillon a été tiré. Pour calculer le la valeur du maximum de vraisemblance, nous formons la fonction log-vraisemblance
Prenez la dérivée de L par rapport à λ et l'assimiler à zéro:
La résolution de λ donne l'estimation du maximum de vraisemblance de λ:
Depuis chaque observation a attente λ donc cela moyenne de l'échantillon. Ce est donc un estimateur sans biais de λ. Ce est également un estimateur efficace, ce est à dire sa variance d'estimation permet d'obtenir la Cramér-Rao (BCR).
Inférence bayésienne
Dans l'inférence bayésienne , la Conjugué avant pour le paramètre de taux λ de la distribution de Poisson est le Distribution Gamma. Laisser
indiquer que λ est distribué selon le Gamma densité g paramétrée en termes de façonner paramètre α et un inverse paramètre d'échelle β:
Ensuite, étant donné le même échantillon de n valeurs k i mesurés comme précédemment, et un avant de Gamma (α, β), la distribution postérieure est
La moyenne a posteriori E [λ] se rapproche l'estimation du maximum de vraisemblance  dans la limite que
dans la limite que 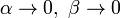 .
.
La distribution prédictive postérieure des données supplémentaire est un Gamma-Poisson (c. binomiale) distribution négative.
La «loi des petits nombres"
La loi de mot est parfois utilisé comme synonyme de distribution de probabilité , et la convergence en droit signifie la convergence dans la distribution. En conséquence, la distribution de Poisson est parfois appelée la loi des petits nombres parce que ce est la distribution de probabilité du nombre d'occurrences d'un événement qui se produit rarement, mais a de très nombreuses occasions de se produire. La loi des petits nombres est un livre écrit par Ladislaus Bortkiewicz sur la distribution de Poisson, publié en 1898 . Certains historiens des mathématiques ont fait valoir que la distribution de Poisson aurait dû se appeler la distribution Bortkiewicz.
Calculer une approximation de la probabilité de Poisson
Lorsque k devient grand (> 20) l'utilisation des journaux et des approximations factorielles sont nécessaires. Voici un exemple écrit en Java.
/ ** Calcule une approximation de la probabilité de Poisson. *param Moyenne - lambda, le nombre moyen d'occurrences *param observé - le nombre réel d'occurrences observées *return ln (probabilité de Poisson) - le logarithme naturel de la probabilité de Poisson. */ public static double poissonProbabilityApproximation ( double mean, int observed ) { double k = observed ; double a = k * Math . log ( mean ) ; double b = - mean ; return a + b - factorialApproximation ( k ) ; } /**Srinivasa Ramanujan ln (n!) D'estimation factorielle. * Bon pour les plus grandes valeurs de n. *return Ln (n!) */ public static double factorialApproximation ( double n ) { if ( n < 2 . ) return 0 ; double a = n * Math . log ( n ) - n ; double b = Math . log ( n * ( 1 . + 4 . * n * ( 1 . + 2 . * n ) ) ) / 6 . ; return a + b + Math . log ( Math . PI ) / 2 . ; }
Outils de visualisation en ligne
- SOCR Répartition GUI
- Interactive Poisson Répartition de TAMU

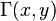 est le Fonction gamma incomplète)
est le Fonction gamma incomplète)