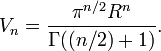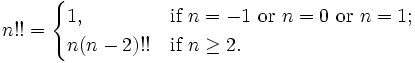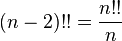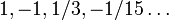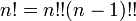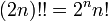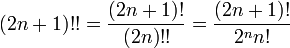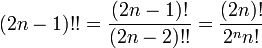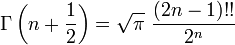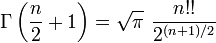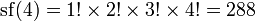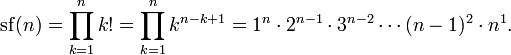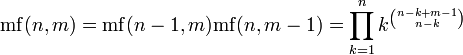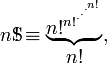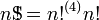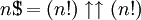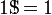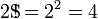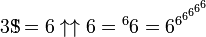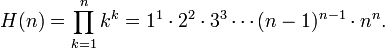Factorielle
À propos de ce écoles sélection Wikipedia
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Mères SOS chaque regard après une une famille d'enfants parrainés .
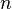 | 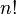 |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 15 | 1307674368000 |
| 20 | 2432902008176640000 |
| 25 | 15511210043330985984000000 |
| 50 | 3.04140932 ... × 10 64 |
| 70 | 1.19785717 ... × 10 100 |
| 450 | 1.73336873 ... × 10 1000 |
| 3249 | 6.41233768 ... × 10 10 000 |
| 25206 | 1,205703438 ... × 10 100 000 |
| 47176 | 8,4485731495 ... × 10 200 001 |
| 100000 | 2,8242294079 ... × 10 456 573 |
En mathématiques , la factorielle d'un non-négative entier n, notée n!, est le produit de l'ensemble des entiers positifs inférieurs ou égaux à n. Par exemple,
- et
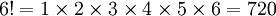
où n! représente n factorielle. La notation n! a été présenté par Christian Kramp en 1808 .
Définition
La fonction factorielle est formellement défini par
La définition ci-dessus incorpore l'instance
comme un exemple du fait que le aucun produit de numéros à tous est 1. Ce fait pour factorielles est utile, parce
- la relation récursive
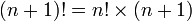 fonctionne pour
fonctionne pour 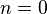 ;
; - cette définition fait de nombreuses identités combinatoire valables pour zéro tailles.
- En particulier, le nombre de combinaisons ou permutations d'un ensemble vide est, tout simplement, une.
Applications
- Factorielles sont utilisés dans la combinatoire . Par exemple, il existe
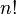 différentes manières de disposer n objets distincts dans une séquence. (Les arrangements sont appelés permutations .) Et le nombre de façons on peut choisir k objets parmi un ensemble donné de n objets (le nombre de combinaisons), est donnée par la soi-disant coefficient binomial
différentes manières de disposer n objets distincts dans une séquence. (Les arrangements sont appelés permutations .) Et le nombre de façons on peut choisir k objets parmi un ensemble donné de n objets (le nombre de combinaisons), est donnée par la soi-disant coefficient binomial
- Dans permutations , si
 les objets peuvent être choisis parmi un total de n objets et disposées de différentes façons, où r ≤ n, alors le nombre total de permutations différentes est donnée par:
les objets peuvent être choisis parmi un total de n objets et disposées de différentes façons, où r ≤ n, alors le nombre total de permutations différentes est donnée par:
- Factorielles se tournent également dans le calcul . Par exemple, le théorème de Taylor exprime une fonction f (x) comme une série de puissance en x, essentiellement parce que la n-ième dérivée de x n est n!.
- Factorielles sont également largement utilisés dans la théorie des probabilités .
- Factorielles sont souvent utilisés comme un exemple simple, avec les nombres de Fibonacci , lors de l'enseignement récursivité en informatique parce qu'ils satisfassent la relation récursive suivante (si n ≥ 1):
La théorie des nombres
Factorielles ont de nombreuses applications dans la théorie des nombres . En particulier, n! est nécessairement divisible par tous les nombres premiers jusqu'à et y compris n. En conséquence, les n> 5 est un nombre composé si et seulement si
Un résultat plus fort est Théorème de Wilson, qui stipule que
si et seulement si p est premier.
Adrien-Marie Legendre a constaté que la multiplicité du nombre premier p survenant dans la factorisation de n! peut être exprimée exactement comme
qui est finie depuis la fonction floor supprime tous 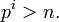
La seule factorielle qui est aussi un nombre premier est 2, mais il ya beaucoup de nombres premiers de la forme 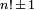 , Appelée nombres premiers factoriels.
, Appelée nombres premiers factoriels.
Tous factorielles supérieur à 0! et une! sont même, car ils sont tous les multiples de deux.
Taux de croissance

Comme n croît, la factorielle n! devient plus grand que tous les polynômes et fonctions exponentielles en n.
Lorsque n est grand, n! peut être estimé assez précisément à l'aide De Stirling le rapprochement:
Une version faible qui peut être facilement prouvé avec induction mathématique est
Le logarithme de la factorielle peut être utilisé pour calculer le nombre de chiffres dans une base donnée la factorielle d'un nombre donné prendra. Il répond à l'identité:
Notez que cette fonction, si graphiquement, est d'environ linéaire, pour de petites valeurs; mais le facteur 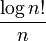 Et de ce fait la pente de la courbe, ne pousse arbitrairement grand, bien que très lentement. Le graphique de la
Et de ce fait la pente de la courbe, ne pousse arbitrairement grand, bien que très lentement. Le graphique de la 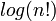 pour
pour 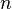 entre 0 et 20 000 est montré dans la figure sur la droite.
entre 0 et 20 000 est montré dans la figure sur la droite.
Un simple approximation pour
basé sur Formule de Stirling est
Une bien meilleure approximation pour
a été donnée par Srinivasa Ramanujan:
On peut voir à partir de ce que
est Ο (n log n). Ce résultat joue un rôle essentiel dans l'analyse de la complexité de calcul algorithmes de tri (voir comparaison tri).
Calcul
La valeur de 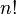 peut être calculé par la multiplication répétée si
peut être calculé par la multiplication répétée si 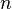 ne est pas trop grand. Le plus grand factorielle que la plupart des calculatrices peuvent gérer est de 69 !, parce que 70! > 10 100 (sauf pour la plupart des calculatrices HP qui peut traiter 253! Comme leur exposant peut être jusqu'à 499). La calculatrice vu dans Mac OS X, Microsoft Excel et Google Calculator peut gérer jusqu'à 170 factorielles !, qui est le plus grand factoriel moins de 2 1024 (10 100 en hexadécimal ) et correspond à un nombre entier de 1 024 bits. Les valeurs 12! et 20! sont les plus grands factorielles qui peuvent être stockés dans, respectivement, les 32 bits et 64 bits entiers couramment utilisés dans les ordinateurs personnels. Dans la pratique, la plupart des applications logicielles seront calculer ces petits factorielles par multiplication directe ou consultation de table. Des valeurs plus élevées sont souvent estimés en termes de estimations à virgule flottante de la Fonction Gamma, généralement avec La formule de Stirling.
ne est pas trop grand. Le plus grand factorielle que la plupart des calculatrices peuvent gérer est de 69 !, parce que 70! > 10 100 (sauf pour la plupart des calculatrices HP qui peut traiter 253! Comme leur exposant peut être jusqu'à 499). La calculatrice vu dans Mac OS X, Microsoft Excel et Google Calculator peut gérer jusqu'à 170 factorielles !, qui est le plus grand factoriel moins de 2 1024 (10 100 en hexadécimal ) et correspond à un nombre entier de 1 024 bits. Les valeurs 12! et 20! sont les plus grands factorielles qui peuvent être stockés dans, respectivement, les 32 bits et 64 bits entiers couramment utilisés dans les ordinateurs personnels. Dans la pratique, la plupart des applications logicielles seront calculer ces petits factorielles par multiplication directe ou consultation de table. Des valeurs plus élevées sont souvent estimés en termes de estimations à virgule flottante de la Fonction Gamma, généralement avec La formule de Stirling.
Pour nombre théorique et combinatoires calculs, très grandes factorielles exactes sont souvent nécessaires. Factorielles Bignum peuvent être calculées par multiplication directe, mais multipliant la séquence 1 × 2 × ... × n de bas en haut (ou top-down) est inefficace; il est préférable de diviser la séquence de manière récursive de telle sorte que la taille de chaque sous-produit est minimisée.
Le asymptotiquement-meilleur rendement est obtenu par le calcul de n! de sa décomposition en facteurs premiers. Tel que documenté par Peter Borwein, factorisation permet 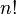 être calculé en temps O (n (log n log log n) 2), à condition que le jeûne algorithme de multiplication est utilisé (par exemple, la Algorithme Schönhage-Strassen). Peter Luschny présente le code source et des repères pour plusieurs algorithmes factoriels efficaces, avec ou sans l'utilisation d'un Premier tamis.
être calculé en temps O (n (log n log log n) 2), à condition que le jeûne algorithme de multiplication est utilisé (par exemple, la Algorithme Schönhage-Strassen). Peter Luschny présente le code source et des repères pour plusieurs algorithmes factoriels efficaces, avec ou sans l'utilisation d'un Premier tamis.
La fonction de gamma

La fonction factorielle peut également être défini pour des valeurs non entières, mais cela nécessite plus d'outils avancés de l'analyse mathématique . La fonction "remplit" les valeurs de la factorielle entre les entiers est appelé le Fonction Gamma, notée 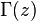 z des nombres entiers pour au moins une, définie par
z des nombres entiers pour au moins une, définie par
D'Euler formule originale pour la fonction Gamma était
La fonction Gamma est liée à factorielles en ce qu'il satisfait une relation récursive similaires:
Avec 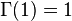 cela donne l'équation pour tout entier naturel
cela donne l'équation pour tout entier naturel 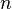 :
:
Sur la base de la valeur de la fonction Gamma pour moitié, l'exemple spécifique de factorielles demi-entier est résolu à
Par exemple
La fonction Gamma, est définie pour tous les nombres complexes 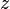 sauf pour les entiers non positive
sauf pour les entiers non positive 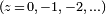 . Il est souvent considéré comme une généralisation de la fonction factorielle au domaine complexe, qui est justifiée pour les raisons suivantes:
. Il est souvent considéré comme une généralisation de la fonction factorielle au domaine complexe, qui est justifiée pour les raisons suivantes:
- Sens commun. La définition canonique de la fonction factorielle partage la même relation récursive avec la fonction Gamma.
- Contexte. La fonction Gamma est généralement utilisé dans un contexte similaire à celui des factorielles (mais, bien sûr, où un domaine plus général est d'intérêt).
- Unicité ( Théorème de Bohr-Mollerup). La fonction Gamma est la seule fonction qui satisfait à la relation récursive précitée pour le domaine des nombres complexes, est méromorphe, et est log-convexe sur l'axe réel positif. Ce est, ce est la seule fonction lisse, connectez-convexe qui pourrait être une généralisation de la fonction factorielle à tous les nombres complexes.
Euler a également développé une approximation de produits convergente pour les factorielles non entiers, qui peuvent être vus comme équivalente à la formule de la fonction Gamma ci-dessus:
Il peut aussi se écrire comme suit:
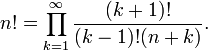
Le produit converge rapidement pour les petites valeurs de n.
Les applications de la fonction gamma
- Les volumes d'un n - dimensions hypersphère est
Produits-factorielle comme
Il existe plusieurs autres séquences entières semblables à la factorielle qui sont utilisés dans les mathématiques:
Primorial
Le primorial (séquence A002110 dans OEIS ) est similaire à la factorielle, mais avec le produit prise seulement sur les nombres premiers .
Double factorielle
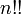 désigne la double factorielle de
désigne la double factorielle de 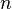 et est définie de manière récursive
et est définie de manière récursive
Par exemple, 8 !! = 2 · 4 · 6 · 8 = 384 et neuf !! = 1 · 3 · 5 · 7 · 9 = 945. La séquence des factorielles doubles (séquence A006882 dans OEIS ) pour 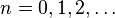 commence comme
commence comme
- 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, ...
La définition ci-dessus peut être utilisé pour définir doubles factorielles de nombres négatifs:
La séquence des factorielles doubles pour 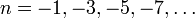 commence comme
commence comme
tandis que la factorielle double d'négatives entiers pairs est infini.
Certaines identités impliquant factorielles sont doubles:
où 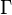 est le Fonction Gamma. La dernière équation ci-dessus peut être utilisé pour définir la factorielle double en fonction d'un nombre complexe
est le Fonction Gamma. La dernière équation ci-dessus peut être utilisé pour définir la factorielle double en fonction d'un nombre complexe 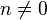 , Tout comme la fonction Gamma généralise la fonction factorielle. Il faut être prudent de ne pas interpréter
, Tout comme la fonction Gamma généralise la fonction factorielle. Il faut être prudent de ne pas interpréter 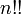 comme la factorielle de
comme la factorielle de 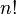 , Ce qui serait écrit
, Ce qui serait écrit 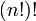 et est un nombre beaucoup plus grand (pour
et est un nombre beaucoup plus grand (pour 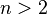 ).
).
Multifactorials
Une notation connexes courante consiste à utiliser plusieurs points d'exclamation pour désigner un multifactorielle, le produit des entiers dans les étapes de deux ( 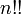 ), Trois (
), Trois ( 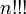 ), Ou plus. Le double factorielle est la variante la plus couramment utilisée, mais on peut de même définir le triple factorielle (
), Ou plus. Le double factorielle est la variante la plus couramment utilisée, mais on peut de même définir le triple factorielle ( 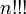 ) Et ainsi de suite. En général, le k ième factoriel, dénotée par
) Et ainsi de suite. En général, le k ième factoriel, dénotée par 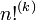 , Est définie par récurrence, comme
, Est définie par récurrence, comme
Certains mathématiciens ont suggéré une alternative de notation 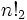 pour la double factorielle et de même
pour la double factorielle et de même 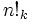 pour d'autres multifactorials, mais cela ne est pas venu dans l'usage général.
pour d'autres multifactorials, mais cela ne est pas venu dans l'usage général.
Factorielle Quadruple
Le factorielle quadruple, cependant, ne est pas un multifactoriel; Ce est un nombre beaucoup plus important donné par 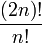 .
.
Superfactorials
Neil Sloane et Simon Plouffe a défini le superfactorial en 1995 comme le produit de la première 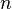 factorielles. Ainsi, le superfactorial de 4 est
factorielles. Ainsi, le superfactorial de 4 est
En général
La séquence de superfactorials commence (à partir 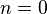 ) Comme
) Comme
- 1, 1, 2, 12, 288, 34 560, 24883200, ... (séquence A000178 dans OEIS )
Cette idée a été étendu en 2000 par Henry Bottomley au superduperfactorial comme le produit de la première 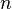 superfactorials, au départ (à partir de
superfactorials, au départ (à partir de 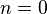 ) Comme
) Comme
- 1, 1, 2, 24, 6912, 238 878 720, 5944066965504000, ... (séquence A055462 dans OEIS )
et ainsi récursive à toute factorielle à plusieurs niveaux où le m e factorielle -niveau de 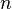 est le produit de la première
est le produit de la première 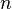
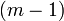 factorielles -Level e, c.-à-
factorielles -Level e, c.-à-
où 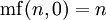 pour
pour 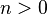 et
et 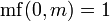 .
.
Superfactorials (définition alternative)
Clifford Pickover dans ses 1995 livres Keys to Infinity défini le superfactorial de 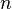 comme
comme
ou que,
où le (4) représente la notation hyper4 opérateur, ou à l'aide Notation des flèches de Knuth,
Cette séquence d'superfactorials commence:
Hyperfactorials
Parfois, le hyperfactorial de 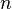 est considéré. Il est écrit que
est considéré. Il est écrit que 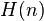 et définie par
et définie par
Pour n = 1, 2, 3, 4, ... les valeurs H (n) sont 1, 4, 108, 27648, ... (séquence A002109 dans OEIS ).
La fonction hyperfactorial est similaire à la factorielle, mais produit un plus grand nombre. Le taux de croissance de cette fonction, cependant, ne est pas beaucoup plus grand qu'un factorielle régulière. Cependant, H (14) = 1,85 × 10 ... 99 est déjà presque égale à un googol, et H (15) = 8,09 × 10 ... 116 est à peu près de la même grandeur que la Nombre de Shannon, le nombre théorique de jeux d'échecs possibles.
La fonction hyperfactorial peut être généralisée à nombres complexes d'une manière similaire à celle de la fonction factorielle. La fonction résulte est appelé K-fonction.

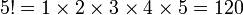
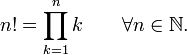
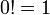
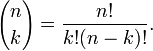
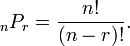
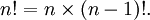
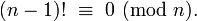
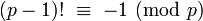
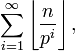
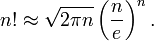
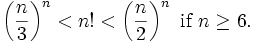
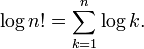
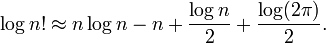
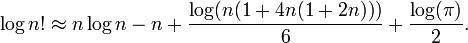
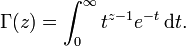
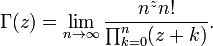
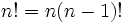
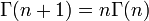
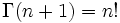
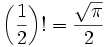
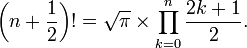
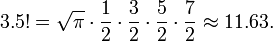
![n! \ Approx \ left [\ left (\ frac {2} {1} \ right) ^ n \ frac {1} {n + 1} \ right] \ left [\ left (\ frac {3} {2} \ right ) ^ n \ frac {2} {n + 2} \ right] \ left [\ left (\ frac {4} {3} \ right) ^ n \ frac {3} {n + 3} \ right] \ dots](../../images/183/18356.png)