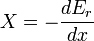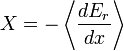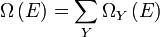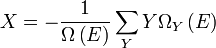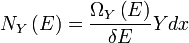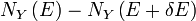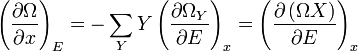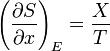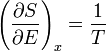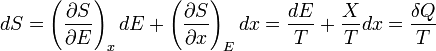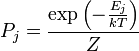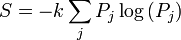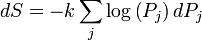Deuxième loi de la thermodynamique
Saviez-vous ...
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Parrainer un enfant de faire une réelle différence.
| Thermodynamique | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Le classique Cycle de Carnot | |||||||||||||||||||||
Branches
| |||||||||||||||||||||
Systèmes État
Processus
Cycles
| |||||||||||||||||||||
|
Propriétés système
Fonctions d'Etat ( Variables conjuguées en italique)
| |||||||||||||||||||||
Propriétés des matériaux
| |||||||||||||||||||||
Équations
| |||||||||||||||||||||
Potentiels
| |||||||||||||||||||||
Philosophie
Histoire
Théories
Principales publications
Échéancier
Art
Éducation
| |||||||||||||||||||||
Les scientifiques
| |||||||||||||||||||||
La deuxième loi de la thermodynamique affirme que la entropie d'un système isolé ne diminue jamais, parce que les systèmes isolés évoluent spontanément vers équilibre thermodynamique-le état d'entropie maximale. De manière équivalente, machines à mouvement perpétuel de la deuxième type sont impossibles.
La seconde loi est une empiriquement validé postulat de la thermodynamique , mais il peut être compris et expliqué en utilisant les sous-jacents quantique mécanique statistique , avec l'hypothèse d'une faible entropie conditions initiales dans le passé lointain (éventuellement au début de l'univers ). Dans le langage de la mécanique statistique, l'entropie est une mesure du nombre de configurations microscopiques correspondant à un état macroscopique. Parce que l'équilibre correspond à une bien plus grande nombre de configurations microscopiques que tout Etat non-équilibre, il a le maximum d'entropie, et la seconde loi suit parce hasard seul garantit pratiquement que le système va évoluer vers l'équilibre.
La seconde loi est considérée comme l'origine de la sens du temps. Ce est l'expression du fait qu'avec le temps, les différences de température, pression, et diminution potentiel chimique dans un isolée non-gravitationnelle système physique, conduisant finalement à un état d'équilibre thermodynamique.
La deuxième loi peut être exprimée de plusieurs manières spécifiques, mais la première formulation est crédité au scientifique français Sadi Carnot en 1824 (voir Chronologie de la thermodynamique).
Description
La première loi de la thermodynamique fournit la définition de base de l'énergie thermodynamique, aussi appelé l'énergie, associée à tous systèmes thermodynamiques, mais inconnu dans la mécanique classique et les États de l'état de conservation de l'énergie dans la nature.
Cependant, le concept de l'énergie dans la première loi ne tient pas compte de l'observation que les processus naturels ont une direction préférentielle de progrès. Par exemple, la chaleur se écoule toujours spontanément à partir de régions de plus haute température à des régions de plus basse température, et jamais l'inverse, à moins que le travail externe est effectuée sur le système. La première loi est complètement symétrique par rapport à l'état initial et final d'un système évolutif. Le concept clé pour l'explication de ce phénomène à travers la seconde loi de la thermodynamique est la définition d'une nouvelle propriété physique, l' entropie .
Un changement dans l'entropie (DS) d'un système est le transfert de chaleur infinitésimale (δ Q) à un système fermé de conduite d'un processus réversible, divisée par la température d'équilibre (T) du système.
L'entropie d'un système isolé qui est en équilibre est constante et a atteint sa valeur maximale.
Pour un corps en équilibre thermique avec un autre, il existe un nombre infini de échelles de température empirique, en général en fonction respectivement sur les propriétés d'un corps thermométrique de référence particulier. Équilibre thermique entre deux corps implique qu'ils ont des températures égales. Le Principe zéro de la thermodynamique dans sa déclaration à court d'habitude permet la reconnaissance que deux corps ont la même température, en particulier celle d'un corps d'épreuve a la même température que un corps thermométrique de référence. La seconde loi permet à une échelle de température distingué, qui définit, un absolu température thermodynamique , indépendante des propriétés de tout organe thermométrique particulier.
La deuxième loi de la thermodynamique peut être exprimée de plusieurs manières spécifiques, les déclarations classiques les plus importants étant la déclaration Rudolph Clausius (1854), la déclaration de Lord Kelvin (1851), et la déclaration en thermodynamique axiomatiques par Constantin Carathéodory (1909). Ces déclarations jettent la loi en termes physiques générales cité par l'impossibilité de certains processus. Le Clausius et les états Kelvin ont été montré pour être équivalent.
Une déclaration plus récente, en raison de George N. Hatsopoulos et Joseph H. Keenan, est: Parmi tous les états d'un système avec des données énergétiques, des composants et paramètres, il existe un équilibre unique et stable qui peut toujours être atteint à partir de tout autre Etat ( avec la même énergie, des composants et paramètres) par un processus de poids réversible. Le Kelvin-Planck, Clausius et déclarations Cathedory peuvent tous être présentés à suivre à partir de la déclaration Hatsopoulos-Keenan.
Déclaration Clausius
Le scientifique allemand Rudolf Clausius jeté les bases de la deuxième loi de la thermodynamique en 1850 en examinant la relation entre le transfert de chaleur et de travail. Sa formulation de la seconde loi, qui a été publié en allemand en 1854, est connue comme la déclaration Clausius:
La chaleur peut jamais passer d'un froid à un corps chaud, sans autre changement, y relative, se produisant en même temps.
La chaleur ne peut pas circuler spontanément de régions froides aux régions chaudes sans travail externe étant effectuée sur le système, ce qui est évident à partir de l'expérience ordinaire de la réfrigération, par exemple. Dans un réfrigérateur, la chaleur passe du froid au chaud, mais seulement lorsqu'il est forcé par un agent extérieur, du système de réfrigération.
Déclaration Kelvin
Lord Kelvin a exprimé la deuxième loi
Il est impossible, à l'aide de l'agent de matière inerte, pour obtenir un effet mécanique de toute partie de la matière en le refroidissant au-dessous de la température la plus froide des objets environnants.
Principe de Carathéodory
Constantin Carathéodory formulé la thermodynamique sur une base axiomatique purement mathématique. Sa déclaration de la seconde loi est connu comme le Principe de Carathéodory, qui peut être formulé comme suit:
Dans chaque quartier d'un État S d'un système adiabatique isolé il ya des états inaccessibles à partir de S.
Avec cette formulation, il a décrit le concept de l'accessibilité adiabatique pour la première fois et a fourni les bases d'une nouvelle sous-zone de la thermodynamique classique, souvent appelés thermodynamique géométriques. Il résulte de principe de Carathéodory cette quantité d'énergie quasi-statique transféré sous forme de chaleur est un holonomique fonction de processus, en d'autres termes, 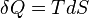 .
.
Bien qu'il est presque coutumier dans les manuels de dire que le principe de Carathéodory exprime la deuxième loi et de le traiter comme équivalente à la Clausius ou aux états de Kelvin-Planck, tel ne est pas le cas. Pour obtenir tout le contenu de la seconde loi, le principe de Carathéodory doit être complétée par le principe de Planck, que le travail isochore augmente toujours l'énergie interne d'un système fermé qui était initialement dans son propre équilibre thermodynamique interne.
Equivalence des états

Supposons qu'il y ait un moteur violer la déclaration Kelvin: ce est à dire, celui qui draine la chaleur et convertit complètement dans le travail de façon cyclique sans autre résultat. Maintenant le coupler avec un inversé Carnot moteur comme indiqué par le graphique. L'effet net et unique de ce moteur nouvellement créé composé des deux moteurs mentionnés est le transfert de chaleur 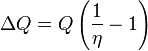 du réservoir refroidisseur à la plus chaude une, qui viole la déclaration Clausius. Ainsi, une violation de la déclaration Kelvin implique une violation de la déclaration de Clausius, Clausius-à-dire la déclaration implique la déclaration Kelvin. Nous pouvons prouver d'une manière similaire que la déclaration Kelvin implique la déclaration Clausius, et donc les deux sont équivalents.
du réservoir refroidisseur à la plus chaude une, qui viole la déclaration Clausius. Ainsi, une violation de la déclaration Kelvin implique une violation de la déclaration de Clausius, Clausius-à-dire la déclaration implique la déclaration Kelvin. Nous pouvons prouver d'une manière similaire que la déclaration Kelvin implique la déclaration Clausius, et donc les deux sont équivalents.
Dans les systèmes de gravitation
Dans les systèmes non-gravitationnelles objets toujours positif la capacité calorifique, ce qui signifie que la température se élève avec l'énergie. Par conséquent, lorsque les flux d'énergie à partir d'un objet à haute température à une une basse température, la température de l'ancien est diminuée tandis que la température de celui-ci est augmenté; où les différences de température ont tendance à diminuer avec le temps.
Cependant, ce ne est pas toujours le cas pour les systèmes où la force gravitationnelle est importante. Les exemples les plus frappants sont les trous noirs, qui - selon la théorie - avoir une capacité thermique négative. Plus le trou noir, plus l'énergie qu'il contient, mais plus sa température. Ainsi, la trou noir supermassif au centre de la voie lactée est censé avoir une température de 10 -14 K, beaucoup plus faible que le fond diffus cosmologique température de 2,7K, mais comme il absorbe les photons du fond diffus cosmologique sa masse est de plus en plus de telle sorte que sa basse température diminue encore avec le temps.
Pour cette raison, les systèmes gravitationnels tendent vers non-même la distribution de la masse et de l'énergie. Bien que ce soit opposée à la façon dont la deuxième loi opère dans d'autres circonstances, il est en fait une consquence de la deuxième loi.
Corollaires
Le mouvement perpétuel de seconde espèce
Avant la création de la deuxième loi, beaucoup de gens qui étaient intéressés à inventer une machine à mouvement perpétuel avaient tenté de contourner les restrictions de la première loi de la thermodynamique en extrayant l'énergie interne massive de l'environnement que la puissance de la machine. Une telle machine est appelée «machine à mouvement perpétuel de seconde espèce". La deuxième loi a déclaré l'impossibilité de ces machines.
Carnot théorème
Le théorème de Carnot (1824) est un principe qui limite l'efficacité maximale pour ne importe quel moteur possible. L'efficacité dépend uniquement de la différence de température entre les réservoirs thermiques chauds et froids. Théorème des états de Carnot:
- Tous les moteurs thermiques irréversibles entre deux réservoirs de chaleur sont moins efficaces qu'un Machine de Carnot fonctionnant entre les mêmes réservoirs.
- Tous les moteurs à chaleur réversibles entre deux réservoirs de chaleur sont également efficaces avec une machine de Carnot fonctionnant entre les mêmes réservoirs.
Dans son modèle idéal, la chaleur de calorique transformée en travail pourrait être rétabli en inversant le mouvement du cycle, un concept connu comme la suite réversibilité thermodynamique. Carnot cependant encore postulé que certains calorique est perdu, ne pas être convertie en travail mécanique. Par conséquent, aucune moteur thermique réel pourrait réaliser le Réversibilité cycle de Carnot et a été condamné à être moins efficace.
Bien que formulée en termes de calories (voir le obsolètes la théorie calorique), plutôt que l'entropie , ce était un premier aperçu de la deuxième loi.
Inégalité de Clausius
Le Clausius Théorème (1854) indique que, dans un processus cyclique
L'égalité a lieu dans le cas réversible et le '<' est irréversible dans le cas. Le boîtier réversible est utilisé pour introduire la fonction Etat entropie . Ce est parce que dans les processus cycliques de la variation d'une fonction de l'Etat est de zéro à partir de la fonctionnalité de l'Etat.
Température thermodynamique
Pour un moteur thermique arbitraire, l'efficacité est la suivante:
où A est le travail effectué par cycle. Ainsi, l'efficacité ne dépend que de q C / H q.
Le théorème de Carnot stipule que tous les moteurs réversibles fonctionnant entre les mêmes réservoirs de chaleur sont également efficaces. Ainsi, ne importe quel moteur à chaleur réversible fonctionnant entre les températures T 1 et T 2 doit avoir la même efficacité, ce est-à-dire, l'efficacité est fonction de la température seulement: 
En outre, un moteur thermique réversible fonctionnant entre les températures T 1 et T 3 doit avoir la même efficacité que l'un consistant en deux cycles, une entre T 1 et une autre (intermédiaire) la température T 2 et la seconde entre T 2 et T 3. Cela ne peut être le cas si
Considérons maintenant le cas où  est une température de référence fixe: la température de la point triple de l'eau. Ensuite, pour chaque T 2 et T 3,
est une température de référence fixe: la température de la point triple de l'eau. Ensuite, pour chaque T 2 et T 3,
Par conséquent, si la température thermodynamique est défini par
alors la fonction f, considérée comme une fonction de la température thermodynamique, est tout simplement
et la température de référence T 1 aura la valeur 273,16. (Bien sûr, ne importe quelle température de référence et une valeur numérique quelconque positifs pourraient être utilisés-le choix ici correspond à la Kelvin échelle.)
Entropy
Selon le Clausius l'égalité, pour un processus réversible
Cela signifie que la ligne intégrante 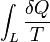 est voie indépendante.
est voie indépendante.
Donc, nous pouvons définir une fonction d'état se appelle l'entropie, qui satisfait
Avec cela, nous ne pouvons obtenir la différence d'entropie en intégrant la formule ci-dessus. Pour obtenir la valeur absolue, nous avons besoin du troisième loi de la thermodynamique , qui stipule que S = 0 au zéro absolu pour les cristaux parfaits.
Pour tout processus irréversible, puisque l'entropie est une fonction d'état, nous pouvons toujours connectons l'état initial et la borne avec un processus réversible imaginaire et l'intégration sur ce chemin de calculer la différence de l'entropie.
Maintenant inverser le processus réversible et le combiner avec ledit processus irréversible. Appliquant L'inégalité de Clausius sur cette boucle,
Ainsi,
où l'égalité tient si la transformation est réversible.
Notez que si le processus est un processus adiabatique, puis 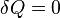 Alors
Alors 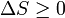 .
.
Disponible travail utile
Un cas particulier important et révélateur idéalisée est de considérer l'application de la deuxième loi au scénario d'un système isolé (appelé le système totale ou univers), composé de deux parties: un sous-système d'intérêt, et l'environnement de la sous-système. Ces environs sont imaginé être si grandes qu'elles peuvent être considérées comme un réservoir de chaleur illimitée à la température T R et la pression P R - sorte que peu importe combien de chaleur est transférée vers (ou depuis) le sous-système, la température de la environnement resteront T R; et ne importe quel point le volume du sous-système se dilate (ou se contracte), la pression de l'environnement restera P R.
Quels que soient les changements à DS et DS R se produisent dans les entropies de le sous-système et les environs individuellement, selon la deuxième loi de l'entropie S tot de l'ensemble du système isolé ne doit pas diminuer:
Selon la première loi de la thermodynamique , le changement du à l'énergie interne du sous-système est la somme de la chaleur AQ ajouté le sous-système, moins toute AW de travail effectué par le sous-système, ainsi que toute l'énergie chimique net entrer dans le sous-système D Σμ iR N i, de sorte que:
où μ iR sont les potentiels chimiques des espèces chimiques dans l'environnement extérieur.
Maintenant, la chaleur quittant le réservoir et entrer dans le sous-système est
où nous avons d'abord utilisé la définition de l'entropie en thermodynamique classique (ou encore, en thermodynamique statistique, la relation entre le changement d'entropie, la température et la chaleur absorbée peut être dérivée); puis la seconde inégalité de droit par le haut.
Il se ensuit donc que toute AW net de travail effectué par le sous-système doit obéir
Il est utile de séparer le AW de travail effectué par le sous-système dans le travail utile AW u qui peut être fait par le sous-système, au-delà du travail p R dV fait simplement par le sous-système en expansion contre la pression externe entourant, donnant la relation suivante pour le travail utile qui peut être fait:
Il est commode de définir la main du côté droit comme dérivé exacte d'un potentiel thermodynamique, appelée la disponibilité ou X exergie du sous-système,
La seconde loi implique donc que pour ne importe quel processus qui peut être considéré comme simplement divisé en un sous-système, et à une température illimité et le réservoir de pression avec laquelle elle est en contact,
ce est à dire le changement de exergie du sous-système ainsi que le travail utile effectué par le sous-système (ou, le changement de exergie du sous-système moins tout travail, complémentaire à celle effectuée par le réservoir de pression, fait sur le système) doit être inférieur ou égal à zéro .
En somme, si un état de référence infinie semblable à un réservoir approprié est choisi comme l'environnement de système dans le monde réel, alors la deuxième loi prévoit une diminution de X pour un processus irréversible et aucun changement pour un processus réversible.
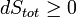 Est équivalent à
Est équivalent à 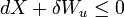
Cette expression avec l'état de référence associé permet une ingénieur de conception de travail à l'échelle macroscopique (au-dessus du limite thermodynamique) d'utiliser la deuxième loi sans mesure directe ou l'étude des changements d'entropie dans un système isolé totale. (Voir aussi ingénieur de procédé). Ces changements ont déjà été examinées par l'hypothèse que le système considéré peut atteindre l'équilibre avec l'état de référence sans altérer l'état de référence. Une efficacité d'un processus ou d'une collection de processus qu'il compare à l'idéal réversibles peuvent également être trouvés (Voir seconde l'efficacité de la loi.)
Cette approche de la deuxième loi est largement utilisé dans l'ingénierie pratique, comptabilité environnementale, écologie des systèmes, et d'autres disciplines.
Histoire
La théorie de la première transformation de chaleur en travail mécanique est due à Nicolas Léonard Sadi Carnot en 1824. Il fut le premier à réaliser correctement que l'efficacité de cette conversion dépend de la différence de température entre un moteur et son environnement.
Reconnaissant l'importance de Le travail de James Prescott Joule sur la conservation de l'énergie, Rudolf Clausius a été le premier à formuler la seconde loi au cours de 1850, sous cette forme: la chaleur ne se écoule pas spontanément du froid au corps chauds. Alors que la connaissance commune maintenant, ce était contraire à la la théorie calorique de chaleur populaire à l'époque, qui a examiné la chaleur comme un fluide. De là, il était en mesure de déduire le principe de Sadi Carnot et la définition de l'entropie (1865).
Fondée au 19ème siècle, le Déclaration de Kelvin-Planck de la deuxième loi dit: «Il est impossible pour ne importe quel appareil qui fonctionne sur une Cycle pour recevoir la chaleur d'un seul réservoir et produire un montant net de travail. "Cela a été démontré pour être équivalent à la déclaration de Clausius.
Le hypothèse ergodique est également important pour la Approche Boltzmann. Il est dit que, sur de longues périodes de temps, le temps passé dans une région de l'espace de phase de micro-avec la même énergie est proportionnelle au volume de cette région, ce est à dire que tous les micro-réduite sont également probables sur une longue période de temps. Équivalente, il est dit que la moyenne de temps et de moyenne sur l'ensemble statistique sont les mêmes.
Il a été montré que non seulement les systèmes classiques, mais aussi de la mécanique quantique ceux tendent à maximiser leur entropie dans le temps. Ainsi, la deuxième loi suit, étant donné les conditions initiales à faible entropie. Plus précisément, il a été montré que la locale von Neumann entropie est à sa valeur maximale avec une très forte probabilité. Le résultat est valable pour une large classe de systèmes quantiques isolés (par exemple un gaz dans un conteneur). Bien que le système complet est pure et n'a donc pas toute l'entropie, le enchevêtrement entre le gaz et le récipient donne lieu à une augmentation de l'entropie locale de l'essence. Ce résultat est l'une des réalisations les plus importantes de thermodynamique quantique.
Aujourd'hui, beaucoup d'efforts dans le domaine tente de comprendre pourquoi les conditions initiales au début de l'univers étaient ceux de basse entropie, car cela est considéré comme l'origine de la seconde loi (voir ci-dessous).
Descriptions informelles
La deuxième loi peut être déclaré de diverses manières, y compris succinctes:
- Il est impossible de produire un travail dans les environs en utilisant un processus cyclique connecté à un seul réservoir de chaleur ( Kelvin , 1851).
- Il est impossible de réaliser un procédé cyclique à l'aide d'un moteur relié à deux réservoirs de chaleur qui aura pour seul effet du transfert d'une quantité de chaleur à partir du réservoir à basse température dans le réservoir à haute température ( Clausius, 1854).
- Si thermodynamique travail est à faire à une vitesse finie, énergie libre doit être dépensé. (Stoner, 2000)
Descriptions mathématiques
En 1856, le physicien allemand Rudolf Clausius a déclaré ce qu'il a appelé la «deuxième théorème fondamental dans le la théorie mécanique de la chaleur »sous la forme suivante:
où Q est la chaleur, T est la température et N est le «équivalence valeur" de toutes les transformations non compensées impliqués dans un processus cyclique. Plus tard, en 1865, Clausius viendrait à définir «l'équivalence de valeur», comme l'entropie. Dans la foulée de cette définition, la même année, la version la plus célèbre de la deuxième loi a été lu lors d'une présentation à la Société philosophique de Zurich le 24 Avril, dans lequel, à la fin de sa présentation, Clausius conclut:
L'entropie de l'univers tend à un maximum.
Cette déclaration est la formulation la plus connue de la deuxième loi. En outre, en raison de la largeur générale de la terminologie utilisée ici, par exemple l'univers , ainsi que le manque de conditions spécifiques, par exemple ouvert, fermé ou isolé, à laquelle cette déclaration se applique, de nombreuses personnes de prendre cette déclaration simple pour signifier que la seconde loi de la thermodynamique se applique pratiquement à tous les sujets imaginables. Ceci, bien sûr, ne est pas vrai; cette déclaration ne est qu'une version simplifiée d'une description plus complexe.
En termes de variation dans le temps, l'énoncé mathématique de la deuxième loi pour une système isolé subir une transformation arbitraire est:
où
- S est l'entropie du système et
- t est le temps .
Le signe d'égalité détient dans le cas que seuls les processus réversibles ont lieu à l'intérieur du système. Si les processus irréversibles ont lieu (ce qui est le cas dans les systèmes réels en fonctionnement) l'> -sign cales. Une autre façon de la formulation de la seconde loi de systèmes isolés est le suivant:
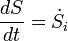 avec
avec 
avec 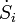 la somme du taux de production d'entropie par tous les processus à l'intérieur du système. L'avantage de cette formulation est qu'elle montre l'effet de la la production d'entropie. Le taux de production d'entropie est un concept très important car il détermine (limites) l'efficacité des machines thermiques. Multipliée par la température ambiante
la somme du taux de production d'entropie par tous les processus à l'intérieur du système. L'avantage de cette formulation est qu'elle montre l'effet de la la production d'entropie. Le taux de production d'entropie est un concept très important car il détermine (limites) l'efficacité des machines thermiques. Multipliée par la température ambiante 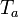 il donne l'énergie dite dissipée
il donne l'énergie dite dissipée 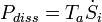 .
.
L'expression de la seconde loi pour les systèmes fermés (donc, permettant l'échange de chaleur et les frontières se déplacent, mais pas l'échange de matière) est:
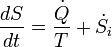 avec
avec 
Ici
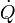 est le flux de chaleur dans le système
est le flux de chaleur dans le système  est la température à l'endroit où la chaleur pénètre dans le système.
est la température à l'endroit où la chaleur pénètre dans le système.
Si la chaleur est fournie au système à plusieurs endroits, nous devons prendre la somme algébrique des termes correspondants.
Pour les systèmes ouverts (permettant également l'échange de la matière):
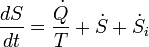 avec
avec 
Ici 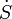 est le flux d'entropie dans le système associé à l'écoulement de matière entrant dans le système. Il ne devrait pas être confondu avec le dérivé de temps de l'entropie. Si la matière est fourni à plusieurs endroits, nous devons prendre la somme algébrique de ces contributions.
est le flux d'entropie dans le système associé à l'écoulement de matière entrant dans le système. Il ne devrait pas être confondu avec le dérivé de temps de l'entropie. Si la matière est fourni à plusieurs endroits, nous devons prendre la somme algébrique de ces contributions.
Mécanique statistique donne une explication pour la deuxième loi en postulant qu'une matière est composée d'atomes et de molécules qui sont en mouvement constant. Un ensemble de positions et les vitesses de chaque particule dans le système est appelé un microscopique du système et en raison du mouvement constant, le système est en constante évolution de son état microscopique. Mécanique statistique postule que, en équilibre, chaque microscopique que le système pourrait être en est également susceptible de se produire, et quand cette hypothèse est faite, elle mène directement à la conclusion que la deuxième loi doit détenir au sens statistique. Autrement dit, la seconde loi se occupent en moyenne, avec une variation statistique de l'ordre de 1 / √ N où N est le nombre de particules dans le système. Pour tous les jours des situations (macroscopiques), la probabilité que la deuxième loi sera violée est pratiquement nulle. Cependant, pour les systèmes avec un petit nombre de particules, les paramètres thermodynamiques, y compris l'entropie, peuvent présenter des écarts statistiques importants de celle prédite par la deuxième loi. La théorie thermodynamique classique ne traite pas de ces variations statistiques.
Dérivation de la mécanique statistique
En raison de Le paradoxe de Loschmidt, dérivations la deuxième loi ont à faire une hypothèse concernant le passé, à savoir que le système est non corrélé à un moment donné dans le passé; ce qui permet pour le traitement probabiliste simple. Cette hypothèse est généralement considéré comme un condition à la limite, et donc la seconde loi est finalement une conséquence des conditions initiales quelque part dans le passé, probablement au début de l'univers (le Big Bang ), si d'autres scénarios ont également été suggérés.
Compte tenu de ces hypothèses, en mécanique statistique, la deuxième loi ne est pas un postulat, ce est plutôt une conséquence de la postulat fondamental , aussi connu comme l'égal postulat de probabilité a priori, tant que l'on est clair que les arguments de probabilité simples sont appliquées que dans la l'avenir, tandis que pour le passé il ya des sources auxiliaires de l'information qui nous disent que ce était la basse entropie. La première partie de la seconde loi, qui stipule que l'entropie d'un système isolé thermiquement ne peut qu'augmenter est une conséquence triviale de l'égalité de postulat de probabilité a priori, si nous limitons la notion de l'entropie des systèmes en équilibre thermique. L'entropie d'un système isolé en équilibre thermique contenant une quantité d'énergie de 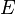 est:
est:
où 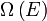 est le nombre d'états quantiques dans un petit intervalle entre
est le nombre d'états quantiques dans un petit intervalle entre 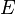 et
et  . Ici
. Ici 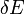 est un macroscopiquement petit intervalle d'énergie qui est maintenu fixe. Strictement parlant, cela signifie que l'entropie dépend du choix de
est un macroscopiquement petit intervalle d'énergie qui est maintenu fixe. Strictement parlant, cela signifie que l'entropie dépend du choix de 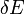 . Cependant, dans la limite thermodynamique (ce est à dire dans la limite des infiniment grande taille du système), l'entropie spécifique (entropie par unité de volume ou par unité de masse) ne dépend pas de
. Cependant, dans la limite thermodynamique (ce est à dire dans la limite des infiniment grande taille du système), l'entropie spécifique (entropie par unité de volume ou par unité de masse) ne dépend pas de 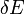 .
.
Supposons que nous ayons un système isolé dont l'état macroscopique est spécifié par un certain nombre de variables. Ces variables macroscopiques peuvent, par exemple, se référer au volume total, les positions des pistons dans le système, etc. Ensuite, 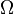 sera fonction des valeurs de ces variables. Si une variable ne est pas fixe (par exemple, nous ne avons pas serrer un piston dans une certaine position), ensuite parce que tous les états accessibles sont également probables en équilibre, la variable libre en équilibre sera telle que
sera fonction des valeurs de ces variables. Si une variable ne est pas fixe (par exemple, nous ne avons pas serrer un piston dans une certaine position), ensuite parce que tous les états accessibles sont également probables en équilibre, la variable libre en équilibre sera telle que 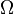 est maximisée car ce est la situation la plus probable en équilibre.
est maximisée car ce est la situation la plus probable en équilibre.
Si la variable a été initialement fixée à une valeur, puis lors de la libération et quand le nouvel équilibre a été atteint, le fait que la variable se ajuster pour que le 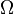 est maximisée, implique que l'entropie aura augmenté ou il aura demeuré le même (si la valeur à laquelle la variable a été fixé se trouvait être la valeur d'équilibre).
est maximisée, implique que l'entropie aura augmenté ou il aura demeuré le même (si la valeur à laquelle la variable a été fixé se trouvait être la valeur d'équilibre).
L'entropie d'un système qui ne est pas en équilibre peut être défini comme suit:
voir ici . Ici, le 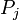 est les probabilités pour que le système se trouvent dans les états étiquetés par l'indice j. A l'équilibre thermique, les probabilités pour les états à l'intérieur de l'intervalle d'énergie
est les probabilités pour que le système se trouvent dans les états étiquetés par l'indice j. A l'équilibre thermique, les probabilités pour les états à l'intérieur de l'intervalle d'énergie 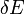 sont tous égaux à
sont tous égaux à 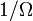 Et dans ce cas la définition générale coïncide avec la définition précédente de S qui se applique au cas de l'équilibre thermique.
Et dans ce cas la définition générale coïncide avec la définition précédente de S qui se applique au cas de l'équilibre thermique.
Supposons que nous partons d'une situation d'équilibre et on enlève tout d'un coup une contrainte sur une variable. Puis juste après nous faisons cela, il ya un certain nombre 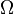 des micro-accessibles, mais l'équilibre n'a pas encore été atteint, de sorte que les probabilités réelles du système étant dans un état accessibles ne sont pas encore égale à la probabilité préalable de
des micro-accessibles, mais l'équilibre n'a pas encore été atteint, de sorte que les probabilités réelles du système étant dans un état accessibles ne sont pas encore égale à la probabilité préalable de 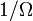 . Nous avons déjà vu que, dans l'état d'équilibre finale, l'entropie aura augmenté ou sont restés les mêmes par rapport à l'état d'équilibre précédente. Boltzmann H-théorème, cependant, prouve que l'entropie augmente en continu en fonction du temps au cours de la sortir intermédiaire de l'état d'équilibre.
. Nous avons déjà vu que, dans l'état d'équilibre finale, l'entropie aura augmenté ou sont restés les mêmes par rapport à l'état d'équilibre précédente. Boltzmann H-théorème, cependant, prouve que l'entropie augmente en continu en fonction du temps au cours de la sortir intermédiaire de l'état d'équilibre.
Dérivation de la variation d'entropie de processus réversibles
La deuxième partie de la deuxième loi affirme que le changement d'entropie d'un système subissant un processus réversible est donné par:
où la température est définie par:
Voir ici pour la justification de cette définition. Supposons que le système dispose d'un paramètre externe, x, qui peut être changé. En général, les états propres de l'énergie du système dépendra de x. Selon le théorème adiabatique de la mécanique quantique, dans la limite d'un changement infiniment lente du hamiltonien du système, le système restera dans le même état propre de l'énergie et donc changer son énergie en fonction de la variation de l'énergie de l'énergie est en état propre.
La force généralisée, X, correspondant à la variable x externe est définie de telle sorte que 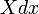 est le travail effectué par le système si x est augmenté d'un montant de dx. Par exemple, si x est le volume, alors X est la pression. La force généralisée d'un système connu pour être en état propre de l'énergie
est le travail effectué par le système si x est augmenté d'un montant de dx. Par exemple, si x est le volume, alors X est la pression. La force généralisée d'un système connu pour être en état propre de l'énergie 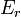 est donné par:
est donné par:
Comme le système peut être dans ne importe quel état propre de l'énergie dans un intervalle de 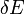 , Nous définissons la force généralisée pour le système que la valeur moyenne de l'expression ci-dessus:
, Nous définissons la force généralisée pour le système que la valeur moyenne de l'expression ci-dessus:
Pour évaluer la moyenne, on partitionne le 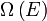 états propres de l'énergie en comptant combien d'entre eux ont une valeur pour
états propres de l'énergie en comptant combien d'entre eux ont une valeur pour 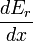 dans un intervalle entre
dans un intervalle entre 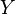 et
et 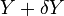 . Appeler ce numéro
. Appeler ce numéro 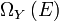 , Nous avons:
, Nous avons:
La moyenne la définition de la force généralisée peut maintenant être écrite:
Nous pouvons relier cela à la dérivée de l'entropie WRT x à l'énergie E constante comme suit. Supposons que nous changeons x à x + dx. Puis 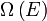 va changer parce que les états propres d'énergie dépendent de x, provoquant états propres de l'énergie de se déplacer dans ou hors de la plage entre
va changer parce que les états propres d'énergie dépendent de x, provoquant états propres de l'énergie de se déplacer dans ou hors de la plage entre 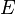 et
et  . Concentrons-nous à nouveau sur les états propres de l'énergie pour lesquels
. Concentrons-nous à nouveau sur les états propres de l'énergie pour lesquels 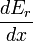 se situe dans la plage comprise entre
se situe dans la plage comprise entre 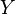 et
et 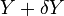 . Depuis ces états propres de l'énergie augmentent en énergie en Y dx, tous ces états propres de l'énergie qui sont dans l'intervalle allant de E - Y dx à E passage de E ci-dessous ci-dessus E. Il ya
. Depuis ces états propres de l'énergie augmentent en énergie en Y dx, tous ces états propres de l'énergie qui sont dans l'intervalle allant de E - Y dx à E passage de E ci-dessous ci-dessus E. Il ya
ces états propres de l'énergie. Si 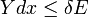 , Tous ces états propres de l'énergie vont se déplacer dans la plage comprise entre
, Tous ces états propres de l'énergie vont se déplacer dans la plage comprise entre 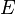 et
et  et de contribuer à une augmentation de la
et de contribuer à une augmentation de la 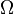 . Le nombre d'états propres de l'énergie qui se déplacent d'en bas
. Le nombre d'états propres de l'énergie qui se déplacent d'en bas  ci-dessus
ci-dessus  est, bien entendu, donnée par
est, bien entendu, donnée par 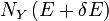 . La différence
. La différence
est donc la contribution nette à l'augmentation de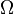 .noter que si Y dx est plus grande que
.noter que si Y dx est plus grande que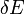 il y aura les états propres de l'énergie qui se déplacent de bas en E ci-dessus
il y aura les états propres de l'énergie qui se déplacent de bas en E ci-dessus .Ils sont comptabilisés à la fois
.Ils sont comptabilisés à la fois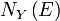 et
et 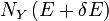 , donc l'expression ci-dessus est également valable dans ce cas.
, donc l'expression ci-dessus est également valable dans ce cas.
Exprimant l'expression ci-dessus comme un dérivé WRT E et en sommant sur Y donne l'expression:
La dérivée logarithmique de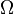 WRT x est donc donnée par:
WRT x est donc donnée par:
Le premier terme est intensif, à savoir qu'il ne se classe pas avec la taille du système. En revanche, les échelles le dernier terme que la taille du système inverse et sera donc disparaît dans la limite thermodynamique. Nous avons ainsi constaté que:
En combinant ceci avec
Donne:
Dérivation pour les systèmes décrits par l'ensemble canonique
Si un système est en contact thermique avec un bain thermique à une certaine température T, puis, à l'équilibre, la distribution de probabilité sur les valeurs propres de l'énergie sont données par l'ensemble canonique:
Ici, Z est un facteur qui normalise la somme de toutes les probabilités à 1, cette fonction est connue comme la fonction de partition. Nous considérons maintenant un changement réversible de la température infinitésimal et dans les paramètres extérieurs sur lesquels les niveaux d'énergie dépendent. Il résulte de la formule générale de l'entropie:
que
Insertion de la formule pour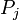 pour l'ensemble canonique en donne ici:
pour l'ensemble canonique en donne ici:
Dérivation général de unitarité de la mécanique quantique
L'opérateur de développement du temps dans la théorie quantique est unitaire, parce que le hamiltonien est hermitienne. En conséquence, la matrice de probabilité de transition est doublement stochastique, ce qui implique la deuxième loi de la thermodynamique. Cette dérivation est assez générale, fondée sur l' entropie de Shannon, et ne nécessite pas d'hypothèses au-delà unitarité, qui est universellement acceptées. Il est une conséquence de l'irréversibilité ou singularité de la matrice de transition générale.
Les Etats non-équilibre
Il est seulement par convention, pour les fins de l'analyse thermodynamique, que toute occasion arbitraire de l'espace-temps est dit être en équilibre thermodynamique. En général, une occasion de l'espace-temps dans la nature ne sont pas en équilibre thermodynamique, lire dans les termes les plus sévères. En termes plus souples, rien dans l'univers entier est ou a jamais été vraiment en équilibre thermodynamique exacte. Si l'on suppose, pour les besoins de l'analyse physique, que l'on a affaire à un système en équilibre thermodynamique, puis statistiquement, il est possible pour ce système d'atteindre des moments de non-équilibre. Dans de tels événements statistiquement peu probable, où des particules chaudes "voler" l'énergie des particules assez froid que le côté froid devient plus froid et le côté chaud devient plus chaud, pour un instant. Ces événements ont été observées à une échelle suffisamment petite, où la probabilité d'une telle chose se passe est important.
La physique impliqué dans ces événements est le thème de la théorème de fluctuation (à ne pas confondre avec le théorème de fluctuation-dissipation), prouvé par Denis Evans et Debra Searles, donne une estimation numérique de la probabilité qu'un système loin de l'équilibre aura un certaine variation d'entropie sur une certaine quantité de temps. Le théorème est démontré avec l'heure exacte équations dynamiques réversibles de mouvement, mais assume l' Axiom de causalité, ce qui équivaut à supposer non corrélées conditions initiales (à savoir, non corrélés dernières). Prédictions quantitatives de ce théorème ont été confirmés dans des expériences de laboratoire à l' Université nationale australienne menées par Edith M. Sevick et al. aide pinces optiques appareil.
Flèche du temps
La deuxième loi de la thermodynamique est la seule loi physique, en dehors decertaines interactions rares en physique des particules, qui est pas symétrique à l'inversion du sens du temps.
La deuxième loi est pensé pour être la raison de la différence entre aller de l'avant et en arrière dans le temps, comme pourquoi la cause précède l'effet (la flèche de causalité de temps).
Controverses
Le démon de Maxwell
James Clerk Maxwell a imaginé un conteneur divisé en deux parties, A et B . Les deux parties sont remplies de la même gaz à des températures égales et placées côte à côte. Observer les molécules des deux côtés, un imaginaire démon garde une trappe entre les deux parties. Quand une molécule plus rapide que la moyenne de A vole vers la trappe, le démon l'ouvre, et la molécule volera de A à B . La moyenne vitesse des molécules dans B aura augmenté tandis que dans A , ils ont ralenti en moyenne. Depuis vitesse moléculaire moyenne correspond à la température, la température diminue en A et une augmentation de B , contrairement à la seconde loi de la thermodynamique.
Une des réponses les plus célèbres à cette question a été proposé en 1929 par Leó Szilárd et plus tard par Léon Brillouin. Szilárd a souligné que la vie réelle du démon de Maxwell aurait besoin d'avoir des moyens de mesure de la vitesse moléculaire, et que l'acte d'acquisition de l'information exigerait une dépense d'énergie. Mais les exceptions ont été trouvés plus tard.
Le paradoxe de Loschmidt
Le paradoxe de Loschmidt, aussi connu comme le paradoxe de la réversibilité, est l'objection selon laquelle il ne devrait pas être possible de déduire un processus irréversible de la dynamique de temps symétrique. Cela met le renversement du temps symétrie de niveau faible presque tous connu des processus physiques fondamentaux en contradiction avec toute tentative d'en déduire la seconde loi de la thermodynamique qui décrit le comportement des systèmes macroscopiques. Ces deux éléments sont des principes bien acceptés en physique, avec le soutien théorique et observationnelle sonore, mais ils semblent être en conflit; où le paradoxe.
En raison de ce paradoxe, dérivations de la deuxième loi doivent faire une hypothèse concernant le passé, à savoir que le système est non corrélé à un certain moment dans le passé, ou - équivalente - que l'entropie dans le passé a été plus faible que dans l'avenir. Cette hypothèse est généralement considéré comme une condition à la limite, et donc la deuxième loi est finalement dérivé des conditions initiales du Big Bang .
Gibbs paradoxe
Dans la mécanique statistique , un simple calcul de la entropie d'un gaz idéal basé sur la distribution de Boltzmann donne une expression de l'entropie qui ne soit pas étendue (est pas proportionnelle à la quantité de gaz en question). Cela conduit à une apparente paradoxe connu comme le paradoxe de Gibbs, permettant, par exemple, l'entropie des systèmes fermés pour diminuer, en violation de la deuxième loi de la thermodynamique.
Le paradoxe est évitée en reconnaissant que l'identité des particules n'a pas d'influence l'entropie. Dans l'explication classique, ceci est associé à une indiscernabilité des particules associées à la mécanique quantique. Cependant, un nombre croissant de documents prendre maintenant la perspective qu'il est simplement la définition de l'entropie qui est changé à ignorer permutation de particules (et ainsi éviter le paradoxe). L'équation résultante pour l'entropie (d'un gaz idéal classique) est vaste, et est connu comme l' équation Sackur-Tetrode.
Poincaré théorème de récurrence
Le Récurrence de Poincaré théorème affirme que certains systèmes seront, après un temps suffisamment long, revenir à un état très proche de l'état initial. Le temps de récurrence de Poincaré est le laps de temps écoulé jusqu'à la récidive, qui est de l'ordre de 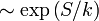 . Le résultat valable pour les systèmes physiques dans lesquels l'énergie est conservée. Le théorème de récurrence contredit apparemment la deuxième loi de la thermodynamique, qui dit que les grands systèmes dynamiques évoluent de façon irréversible vers l'état d'entropie plus élevé, de sorte que si l'on part d'un état de faible entropie, le système ne sera jamais revenir. Il ya plusieurs façons possibles pour résoudre ce paradoxe, mais aucun d'entre eux est universellement acceptées. L'argument le plus raisonnable est que pour les systèmes thermodynamiques typiques du temps de récurrence est si grande (de nombreuses fois plus longue que la durée de vie de l'univers) qui, à toutes fins pratiques, on ne peut pas observer la récurrence.
. Le résultat valable pour les systèmes physiques dans lesquels l'énergie est conservée. Le théorème de récurrence contredit apparemment la deuxième loi de la thermodynamique, qui dit que les grands systèmes dynamiques évoluent de façon irréversible vers l'état d'entropie plus élevé, de sorte que si l'on part d'un état de faible entropie, le système ne sera jamais revenir. Il ya plusieurs façons possibles pour résoudre ce paradoxe, mais aucun d'entre eux est universellement acceptées. L'argument le plus raisonnable est que pour les systèmes thermodynamiques typiques du temps de récurrence est si grande (de nombreuses fois plus longue que la durée de vie de l'univers) qui, à toutes fins pratiques, on ne peut pas observer la récurrence.
la mort thermique de l'univers
Selon la deuxième loi, l'entropie d'un système isolé, comme l'univers entier, ne diminue jamais. Si l'entropie de l'univers n'a pas de limite supérieure au maximum puis finalement l'univers aura pas d' énergie libre pour soutenir le mouvement ou la vie , qui est, la mort de la chaleur est atteint.
Citations
| Wikiquote a une collection de citations liées à: Deuxième loi de la thermodynamique |
La loi que l'entropie augmente toujours titulaire, je pense, la position suprême parmi les lois de la nature. Si quelqu'un fait remarquer pour vous que votre théorie de l'animal de compagnie de l' univers est en désaccord avec les équations de Maxwell - alors tant pis pour les équations de Maxwell. Si elle se trouve être contredit par l'observation - ainsi, ces expérimentateurs font des choses Bungle parfois. Mais si votre théorie est jugée contre la deuxième loi de la thermodynamique, je peux vous donner aucun espoir; il n'y a rien pour elle, mais à l'effondrement dans la plus profonde humiliation.-SirArthur Stanley Eddington,La nature du monde physique(1927)
La tendance à l'entropie d'augmenter dans les systèmes isolés est exprimée dans la deuxième loi de la thermodynamique - peut-être la formulation la plus pessimiste et amorale dans toute la pensée humaine.- Gregory Hill etKerry Thornley, Principia Discordia(1965)
Il ya eu presque autant de formulations de la deuxième loi comme il ya eu des discussions d'elle.-Philosopher / PhysicienPW Bridgman, (1941)

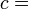
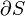
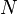
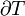
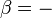
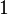
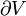
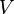
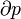
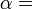
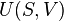
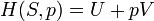
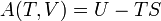
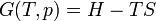
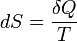
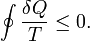
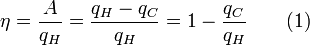
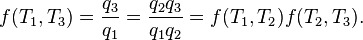
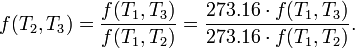
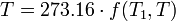

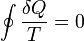
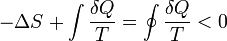
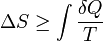
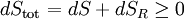
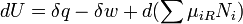
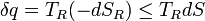
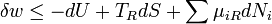
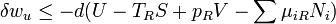
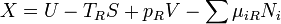
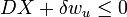


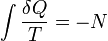
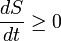
![S = k \ log \ left [\ Omega \ left (E \ right) \ right] \,](../../images/2567/256780.png)
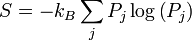
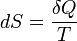
![\ Frac {1} {k T} \ equiv \ beta \ equiv \ frac {d \ log \ left [\ Omega \ left (E \ right) \ right]} {de}](../../images/2567/256788.png)