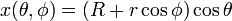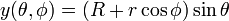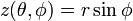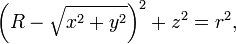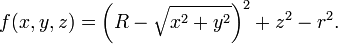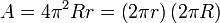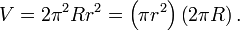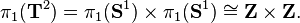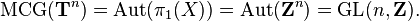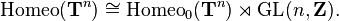Torus
À propos de ce écoles sélection Wikipedia
SOS croit que l'éducation donne une meilleure chance dans la vie des enfants dans le monde en développement aussi. Parrainer un enfant de faire une réelle différence.


En géométrie , un tore (pl. tori) est un surface de révolution générée en faisant tourner un cercle dans l'espace à trois dimensions autour d'un axe coplanaires avec le cercle. Si l'axe de révolution ne touche pas le cercle, la surface a une forme d'anneau et est appelé un tore de anneau ou tore tout simplement si la forme de l'anneau est implicite.
Lorsque l'axe est tangente au cercle, la surface résultante est appelée un tore de corne; lorsque l'axe est une corde du cercle, il est appelé une broche tore. Un cas dégénéré, ce est quand l'axe est un diamètre du cercle, qui génère simplement la surface d'une sphère . Le tore anneau délimite un solide connue comme un tore. Toroïdale adjectif peut être appliqué à tori, tores ou, plus généralement, toute forme d'anneau comme dans inducteurs et transformateurs toriques. Exemples du monde réel de (environ) objets toriques comprennent beignets, vadais, chambres à air, bagels, beaucoup bouées de sauvetage, Joints toriques et anneaux tourbillonnaires.
En topologie , un tore de bague est homéomorphe à l'cartésienne produit de deux cercles : S 1 × S 1, et celui-ci, est égale à la définition dans ce contexte. Ce est un compact 2-variété du genre 1. Le tore anneau est une façon d'intégrer cet espace dans l'espace euclidien , mais une autre façon de le faire est le produit cartésien de l'intégration des S 1 dans le plan. Cela produit un objet géométrique appelé Clifford tore, en surface 4-espace.
Le mot vient du tore latine sens des mots coussin.
Géométrie





Un tore peut être définie paramétriquement par:
où
- θ, φ sont des angles qui font un cercle complet, en commençant à 0 et se terminant à 2π, de sorte que leurs valeurs commencent et se terminent au même point,
- R est la distance entre le centre du tube au centre du tore,
- r est le rayon du tube.
R et R sont également connus comme le "rayon majeur" et "mineur rayon", respectivement. Le rapport des deux est connu comme le " rapport d'aspect ". Un anneau a un rapport d'aspect d'environ 2 à 3.
Une équation implicite en coordonnées cartésiennes pour un tore symétrie radiale sur le z - axe est
ou la solution de f (x, y, z) = 0, où
Éliminant Algébriquement la racine carrée donne une équation quartique,
Les trois classes différentes de tores normalisées correspondent aux trois dimensions relatives possibles de R et R. Lorsque R> r, la surface sera l'anneau tore familier. Le cas R = r correspond à tore de corne, qui est en fait un tore sans "trou". Le cas R <r décrit les tore de broche auto-intersection. Lorsque R = 0, le tore dégénère à la sphère.
Le aire de surface et l'intérieur du volume de ce tore sont facilement calculées à l'aide Barycentre théorème de Pappus dons
Ces formules sont les mêmes que pour un cylindre de rayon R et r de longueur, créé en découpant le tube et la déroulant en redressant la ligne passant à travers le centre du tube. Les pertes de surface et de volume sur le côté intérieur du tube annulent exactement les gains sur le côté extérieur.
En tant que tore est le produit de deux cercles, une version modifiée du système de coordonnées sphérique est parfois utilisé. Dans sphérique traditionnelle coordonnées il ya trois mesures, R, la distance du centre du système de coordonnées, et les angles θ et φ, mesurée à partir du point central. Comme un tore a, effectivement, deux points centraux, les points centraux des angles sont déplacés; φ mesures le même angle comme il le fait dans le système sphérique, mais il est connu que la direction "toroïdal". Le point de θ centre est déplacé vers le centre de r, et est connue comme la direction "poloïdale". Ces termes ont été utilisés d'abord dans une discussion du champ magnétique de la Terre, où "poloïdale" a été utilisé pour désigner "la direction vers les pôles". Lors de l'utilisation moderne, ces termes sont plus communément utilisés pour discuter de dispositifs de fusion magnétique de confinement.
Topologie
Topologiquement , un tore est un fermé défini comme la surface produit de deux cercles : S 1 × S 1. Cela peut être considéré comme se trouvant dans C 2 et est un sous-ensemble de la 3-sphère S 3 de rayon √2. Ce tore topologique est également souvent appelé le Clifford tore. En fait, S 3 est rempli par une famille de tores imbriqués de cette manière (avec deux cercles dégénérés), ce qui est important dans l'étude des 3 S en tant que faisceau de fibres sur S 2 ( Hopf bundle).
La surface décrite ci-dessus, compte tenu de la topologie relative de R 3, est homéomorphe à un tore topologique tant qu'elle ne coupe pas son propre axe. Un homéomorphisme particulière est donnée par projetant stéréographiquement le tore topologique en R 3 du pôle nord de S 3.
Le tore peut également être décrit comme un quotient du plan cartésien dans les identifications
- (X, y) ~ (x 1, y) ~ (x, y 1).
Ou, de manière équivalente, comme le quotient de la carré unité en collant les bords opposés ensemble, décrit comme un ABA polygone fondamentale -1 B -1.
Le groupe fondamental du tore est que le produit direct du groupe fondamental du cercle avec lui-même:
Intuitivement, cela signifie qu'un fermé chemin qui fait le tour du tore '«trou» (par exemple, un cercle qui trace une latitude notamment), puis les cercles les tore' «corps» (par exemple, un cercle qui trace une longitude particulier) peut être déformée à un chemin que les cercles le corps puis le trou. Donc, strictement «latitude» et strictement chemins «longitudinale» trajet. Cela pourrait être imaginé comme deux lacets traversant l'autre, puis déroulement, puis rembobinage.
Si un tore est percé et tourné à l'envers puis un autre tore résultats, avec des lignes de latitude et de longitude échangés.
La première groupe d'homologie du tore est isomorphe au groupe fondamental (cela résulte de Théorème d'Hurewicz puisque le groupe est fondamentale abélien).
Couvercle en deux bâchés
Le 2-tore double couvre la 2-sphère, avec quatre des points de ramification. Chaque Structure conforme à la 2-tore peut être représenté par un couvercle en forme de feuille à deux du 2-sphère. Les points sur le tore correspondant aux points de ramification sont le Points de Weierstrass. En fait, le type du tore conforme est déterminée par la birapport des quatre points.
n tore de dimension
Le tore a une généralisation à des dimensions supérieures, les n - tore dimensions, souvent appelé le n - tore ou hypertore pour faire court. (Ce est l'un des deux sens différents du terme "n -torus".) Rappelant que le tore est l'espace de produit de deux cercles, le tore de dimension n est le produit de n cercles. C'est:
Le tore est discuté ci-dessus le tore deux dimensions. Le tore de dimension 1 est juste le cercle. Tout comme pour le 2-tore, le n -torus peut être décrit comme un quotient de R n sous déplacements solidaires l'une quelconque de coordonnées. Autrement dit, le n -torus est R n modulo le l'action de l'entier réseau Z n (avec l'action étant considérée comme l'addition de vecteurs). De manière équivalente, le n -torus est obtenu à partir de l'extrémité N de dimension hypercube par collage le contraire face ensemble.
Un n -torus dans ce sens est un exemple de n dimensions compactes collecteur . Ce est également un exemple d'un compact abélienne groupe de Lie. Cela découle du fait que le cercle unité est un groupe de Lie abélien compact (lorsqu'il est identifié avec l'unité des nombres complexes avec multiplication). la multiplication de groupe sur le tore est alors définie par coordonner sage multiplication.
Groupes toriques jouent un rôle important dans la théorie de groupes de Lie compacts. Cela est dû en partie au fait que, dans un groupe de Lie compact G on peut toujours trouver un tore maximal; ce est, un fermé sous-groupe qui est un tore de la plus grande dimension possible. Cette maximale tori T ont un rôle à jouer dans le contrôle théorie de G connecté.
Automorphismes de T sont facilement construits à partir automorphismes du réseau Z n, qui sont classés par M matrices intégrante de taille n × n qui sont inversible intégrale inverse; Ce sont juste les M intégrante de déterminant +1 ou -1. Faire M agissent sur R n de la manière habituelle, on a l'automorphisme Toral typique sur le quotient.
Le groupe fondamental d'un n -torus est un groupe abélien libre de rang n. Le k ième groupe d'homologie d'un n -torus est un groupe abélien libre de rang n choisir k. Il se ensuit que la caractéristique d'Euler de la -torus n est égal à 0 pour tout n. Le anneau de cohomologie H • (T n, Z) peut être identifié avec le algèbre extérieure sur la Z - Module Z n dont les générateurs sont les duals des cycles n non triviaux.
l'espace de configuration
Comme le -torus n est le produit de n -fois du cercle, le n -torus est le espace de configuration de n ordonné, pas nécessairement des points distincts sur le cercle. Symboliquement, T n = (S 1) n. L'espace de configuration de non ordonnées points, pas nécessairement distincts est donc la orbifold T n / S n, qui est le quotient du tore par la groupe symétrique sur n lettres (par permutation des coordonnées).
Pour n = 2, le quotient est le Möbius bande, le bord correspondant aux points où les deux orbifold coordonnées coïncident. Pour n = 3 ce quotient peut être décrite comme un tore plein avec une section transversale triangle équilatéral, avec une touche; de manière équivalente, comme un prisme triangulaire dont les faces supérieure et inférieure sont reliées avec une touche ⅓ (120 °): les intérieurs correspond à trois dimensions les points de la 3-tore où toutes les coordonnées 3 sont distincts, le visage deux dimensions correspond à deux points de coordonnées égalité et la 3ème différente, tandis que le bord de dimension 1 correspond à des points avec tous les 3 coordonnées identiques.
Ces orbifolds ont trouvé significative applications à la théorie de la musique dans le travail de Dmitri Tymoczko et collaborateurs (Felipe Posada et Michael Kolinas, et al.), utilisées pour modéliser triades musicales.
Tore plat
Le tore plat est un tore avec la métrique hérité de sa représentation comme quotient, R 2 / Z 2, du plan cartésien dans les identifications (x, y) ~ (x 1, y) ~ (x, y 1). Cela lui donne la structure d'un Variété riemannienne.
Cette mesure peut également être réalisé par incorporations spécifiques du familier 2-tore dans euclidienne 4-espace ou dimensions supérieures. Sa surface a zéro Courbure gaussienne partout. Sa surface est «plat» dans le même sens que la surface d'un cylindre est "plat". En trois dimensions, on peut plier une feuille de papier plane dans un cylindre sans étirer le papier, mais vous ne pouvez pas puis pliez ce cylindre dans un tore sans étirer le papier (sauf si vous abandonnez certaines conditions de régularité et différentiabilité, voir ci-dessous). En quatre dimensions on peut (mathématiquement).
Un simple 4 -d plongement euclidien est comme suit: <x, y, z, w> = <R cos (u), R sin (u), P cos (v), P sin (v)> où R et P sont des constantes déterminant le rapport d'aspect. C'est difféomorphe à un tore régulière mais pas isométrique. Il ne peut pas être intégré dans isométrique euclidienne 3-espace. Cartographie en trois -espace vous oblige à étirer, dans ce cas, il ressemble à un tore régulière, par exemple, la carte suivante <x, y, z> = <(R + P sin (v)) cos (u) (R + P sin (v)) sin (u), P cos (v)>.
Un tore plat les partitions 3-sphère en deux congruentes sous-ensembles de tori solides avec la surface du tore plat précité comme leur commune limite.
Récemment (Avril 2012), un plongement d'un tore plat en trois dimensions a été trouvé. Il se agit d'une structure semblable à une fractale comme il est réalisé par ondulation de façon répétée un tore normal. Comme fractales, il n'a pas défini la courbure gaussienne. Cependant, contrairement fractales, il ne ont défini les normales de surface.
n tore -fois
Dans la théorie de surfaces il ya un autre objet, le tore n -fois. Au lieu du produit de n cercles, un tore de n -fois est le somme connexe de n tori 2 dimensions. Pour former une somme de deux surfaces connecté, supprimer l'une de l'intérieur du disque et une "colle" les surfaces ensemble le long des cercles de délimitation de disques. Pour former la somme connectée de plus de deux surfaces, somme deux d'entre eux à un moment jusqu'à ce qu'ils soient tous connectés. En ce sens, un n -torus ressemble à la surface de n beignets collées côte à côte, ou deux dimensions sphère avec n poignées fixées.
Un tore ordinaire est un tore une fois, 2 fois tore est appelé tore doubles, 3 fois un tore tore triple, et ainsi de suite. Le tore n -fois est dit être un " surface orientable "de" genre "n, le genre étant le nombre de poignées. Le tore 0 est le facteur deux dimensions sphère .
Le Théorème de classification pour les surfaces stipule que chaque compacte surface connexe est soit une sphère, un tore de -fois n avec n> 0, ou la somme connexe de n plans projectifs (ce est-plans projectifs sur les nombres réels ) avec n> 0.
 tore doubles |  tore triple |
Toroïdal polyèdres
Polyèdres avec le type topologique de tore sont appelés polyèdres toroïdale, et satisfaire une version modifiée de la formule de polyèdre , E - F - V = 0.
Le terme «toroïdal Polydron" est également utilisé pour les polyèdres ultérieure genre et pour des immersions de polyèdres toroïdal.
Automorphismes
Le groupe homéomorphisme (ou le sous-groupe des difféomorphismes) du tore est étudiée dans topologie géométrique. Son groupe de mapping class (le groupe de composants connectés) est isomorphe au groupe GL (n, Z) de matrices d'entiers inversibles, et peut être réalisé comme cartes linéaires sur l'espace de revêtement universel R n qui préservent la norme réseau Z n (ce qui correspond à coefficients entiers) et donc descendre au quotient.
Au niveau de l'homotopie et homologie, le groupe de classe de cartographie peut être identifié que l'action sur le premier homologie (ou de manière équivalente, première cohomologie, ou sur le groupe fondamental, car ce sont tous naturellement isomorphe; noter également que le premier groupe de cohomologie génère l'algèbre de cohomologie):
Étant donné que le tore est un Eilenberg-MacLane espace K (G, 1), ses équivalences d'homotopie, à homotopie près, peut être identifié avec automorphismes du groupe fondamental); que ce est d'accord avec le groupe de classe de cartographie reflète que tous les équivalences d'homotopie peuvent être réalisées par homéomorphismes - chaque équivalence d'homotopie est homotope à un homéomorphisme - et que homéomorphismes homotopes sont en fait isotopique (relié par homéomorphismes, non seulement grâce à des équivalences d'homotopie). De façon plus concise, la carte Homeo (T n) → SHE (T n) est 1 connecté (isomorphe sur le chemin-composants, sur groupe fondamental). Ce est un "homéomorphisme réduit à homotopie réduit à l'algèbre" résultat.
Ainsi, la courte séquence exacte du groupe de classe de cartographie divise (une identification du tore comme le quotient de R n donne un fractionnement, via les applications linéaires, comme ci-dessus):
de sorte que le groupe homéomorphisme du tore est une produit semi-direct,
Le groupe de classe de la cartographie de la hausse des surfaces de genre est beaucoup plus compliqué, et un domaine de recherche actif.
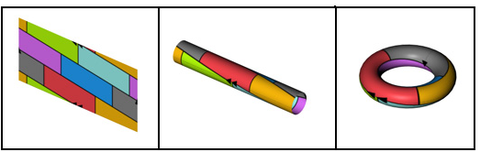
Coloriage un tore
Si un tore est divisé en régions, il est toujours possible de colorer les régions avec pas plus de sept couleurs de sorte que les régions voisines ont des couleurs différentes. (Contraste avec le théorème des quatre couleurs pour le plan .)
Couper un tore
Un tore norme (spécifiquement, un tore d'anneau) peut être coupé avec n plans en au plus
pièces.
Les conditions initiales de cette séquence pour n à partir de 1 sont:
- 2, 6, 13, 24, 40, ... (séquence A003600 dans OEIS ).