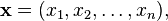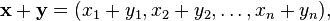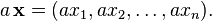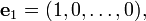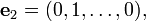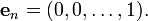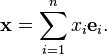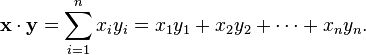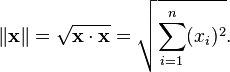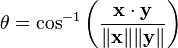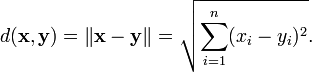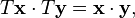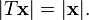Espace euclidien

Autour 300 BC , le grec mathématicien Euclide a entrepris une étude des relations entre les distances et les angles , d'abord dans un plan (une surface plane idéalisée), puis dans l'espace. Un exemple d'une telle relation est que la somme des angles d'un triangle est toujours 180 degrés. Aujourd'hui, ces relations sont connus comme deux et trois dimensions géométrie euclidienne .

Dans moderne mathématique langue, la distance et l'angle peuvent être généralisés facilement aux espaces de dimension 4, 5 dimensions, et même de dimensions supérieures. Un espace de dimension n avec les notions de distance et l'angle qui obéissent aux relations euclidiennes est appelé un espace de dimension euclidienne de n. La plupart de cet article est consacrée au développement de la langue moderne nécessaire pour le saut conceptuel à des dimensions supérieures.

Une propriété essentielle d'un espace euclidien est sa planéité. Autres espaces existent dans la géométrie euclidienne qui ne sont pas. Par exemple, la surface d'une sphère est pas; un triangle sur une sphère (défini convenablement) aura des angles qui résument à quelque chose supérieur à 180 degrés. En fait, il se agit essentiellement d'un seul espace euclidien de chaque dimension, alors qu'il ya de nombreux espaces non-euclidiennes de chaque dimension. Souvent, ces autres espaces sont construits en déformant systématiquement espace euclidien.

Aperçu intuitive

Une façon de penser du plan euclidien est comme un ensemble de points satisfaisant certaines relations, exprimables en termes de distance et l'angle. Par exemple, il existe deux opérations fondamentales de l'avion. Un est traduction, ce qui signifie un déplacement du plan de sorte que chaque point est décalé dans le même sens et par la même distance. L'autre est rotation autour d'un point fixe dans le plan, dans lequel tous les points dans le plan tourne autour de ce point fixe du même angle. L'un des principes de base de la géométrie euclidienne est que deux chiffres (ce est- sous-ensembles ) du plan devraient être considérées comme équivalentes ( congruent) si l'on peut être transformé en l'autre par une séquence de translations et des rotations. (Voir Groupe euclidien.)

Afin de rendre tout cela mathématiquement précise, il faut définir clairement les notions de distance, l'angle, la traduction et la rotation. La méthode standard pour ce faire, tel que réalisé dans le reste de cet article, est de définir le plan euclidien comme deux dimensions réel espace vectoriel équipé d'un produit interne. Car alors:

• la des vecteurs dans l'espace de vecteur correspondent aux points du plan euclidien,
• l' addition opération dans l'espace de vecteur correspond à la traduction, et
• le produit scalaire implique notions d'angle et de distance, qui peuvent être utilisés pour définir rotation.

Une fois le plan euclidien a été décrite dans cette langue, il est en fait une simple question d'étendre son concept aux dimensions arbitraires. Pour la plupart, le vocabulaire, les formules et les calculs ne sont pas plus difficiles faites par la présence de plusieurs dimensions. (Toutefois, les rotations sont plus subtiles dans les dimensions élevées, et la visualisation des espaces de grande dimension reste difficile, même pour les mathématiciens expérimentés.)

Une ride finale est que l'espace euclidien ne est pas techniquement un espace vectoriel, mais plutôt une espace affine, sur lequel un espace vectoriel actes. Intuitivement, la distinction dit simplement qu'il n'y a pas le choix canonique de où le origine devrait aller dans l'espace, car il peut être traduit partout. Dans cet article, cette technicité est largement ignoré.

Réel espace de coordonnées

Soit R le champ de nombres réels . Pour toute non-négative entier n, l'espace de tous les n - uplets de nombres réels forme un espace vectoriel de dimension n sur R, qui est notée R ⁿ et parfois appelé réel espace de coordonnées. Un élément de R ⁿ est écrit

où chaque x _i est un nombre réel. Les opérations spatiales vectoriel sur R ⁿ sont définis par

L'espace vectoriel R ⁿ est livré avec un base standard:

Un vecteur arbitraire dans R ⁿ peut alors se écrire sous la forme

R ⁿ est l'exemple prototypique d'un espace vectoriel de dimension n réelle. En fait, chaque réelle n espace vectoriel de dimension V est isomorphe à R ^n. Ce ne est pas isomorphisme canonique, cependant. Un choix d'isomorphisme est équivalent à un choix de base de V (en regardant l'image de la norme de base pour R ⁿ en V). La raison pour travailler avec des espaces vectoriels arbitraires au lieu de R ⁿ est qu'il est souvent préférable de travailler d'une manière de coordonner-libre (ce est, sans choisir une base préférée).

La structure euclidienne

Espace euclidien est plus que juste un véritable espace de coordonnées. Afin d'appliquer la géométrie euclidienne, il faut être en mesure de parler des distances entre les points et les angles entre les lignes ou des vecteurs. La voie naturelle pour obtenir ces grandeurs est en introduisant et en utilisant le produit scalaire standard (également connu sous le nom produit scalaire) sur R ^n. Le produit scalaire des deux vecteurs de x et y est défini par

Le résultat est toujours un nombre réel. En outre, le produit scalaire de x par lui-même est toujours positif ou nul. Ce produit nous permet de définir la "longueur" d'un vecteur x comme

Cette fonction de longueur satisfait les propriétés requises d'un norme et est appelée la norme euclidienne de R ^n.

Le (non obtus) angle θ (0 ° ≤ θ ≤ 180 °) entre x et y est donnée par

où cos ^-1 est le arccosinus fonction.

Enfin, on peut utiliser la norme pour définir une métrique (ou fonction de distance) sur R ⁿ par

Cette fonction de distance est appelée Métrique euclidienne. Il peut être considéré comme une forme de théorème de Pythagore .

Réel espace de coordonnées avec cette structure euclidienne est appelé espace euclidien et souvent notée E ^n. (De nombreux auteurs se réfèrent à R ⁿ lui-même comme l'espace euclidien, avec la structure euclidienne étant entendu). La structure euclidienne E ⁿ fait un espace de produit intérieur (en fait une Espace de Hilbert), un espace vectoriel normé, et un espace métrique.

Rotations de l'espace euclidien sont alors définis comme orientation de préservation linéaire Transformations T qui préservent les angles et les longueurs:

Dans le langage des matrices , les rotations sont matrices orthogonales spéciales.

Topologie de l'espace euclidien

Depuis l'espace euclidien est un espace métrique est également un espace topologique avec le naturel topologie induit par l'indicateur. La topologie métrique sur E ⁿ se appelle la topologie euclidienne. Un ensemble est ouverte dans la topologie euclidienne si et seulement se il contient un boule ouverte autour de chacun de ses points. La topologie euclidienne se avère être l'équivalent de la topologie produit sur R ⁿ considéré comme un produit de n copies de la droite réelle R (avec sa topologie standard).

Un résultat important de la topologie de R ^n, qui est loin d'être superficielle, est Brouwer invariance de domaine. Tout sous-ensemble de R ⁿ (avec son Topologie induite) ce est homéomorphe à un autre sous-ensemble ouvert de R ⁿ est elle-même ouverte. Une conséquence immédiate est que R ^m ne est pas homéomorphe à R ⁿ si m ≠ n - un intuitivement "évidente" résultat qui est néanmoins difficile à prouver.

Généralisations

En mathématiques modernes, espaces euclidiens forment les prototypes pour d'autres, des objets géométriques plus complexes. Par exemple, un variété lisse est un Séparé de l'espace topologique qui est localement difféomorphe à l'espace euclidien. Difféomorphisme ne respecte pas la distance et l'angle, de sorte que ces concepts clés de la géométrie euclidienne est perdu sur une variété lisse. Toutefois, si l'on prescrit en outre un produit scalaire variant doucement sur le collecteur de espaces tangents, alors le résultat est ce qu'on appelle une Variété riemannienne. Autrement dit, une variété riemannienne est un espace construit par déformation et recollant espaces euclidiens. Tel espace bénéficie notions de distance et l'angle, mais ils se comportent dans un incurvée de manière, non-euclidienne. Le plus simple variété riemannienne, constitué de R ⁿ avec un produit intérieur constant, est essentiellement identique à euclidiens n se -Espace.

Si l'on modifie un espace euclidien de sorte que son produit interne devient négatif dans une ou plusieurs directions, puis le résultat est un l'espace pseudo-euclidien. Variétés lisses construites à partir de ces espaces sont appelés collecteurs de pseudo-riemannienne. Peut-être leur application la plus célèbre est la théorie de la relativité , où vide espace-temps sans question est représenté par l'espace pseudo-euclidien plat appelé L'espace de Minkowski, espaces-temps avec de la matière dans les autres forment des collecteurs pseudo-riemannien, et la gravité correspondant à la courbure d'un tel collecteur.

Notre univers, être soumis à la relativité, ne est pas euclidienne. Cela devient important dans des considérations théoriques de l'astronomie et de la cosmologie , et aussi dans certains problèmes pratiques tels que positionnement global et avion la navigation. Néanmoins, un modèle euclidien de l'univers peut encore être utilisé pour résoudre de nombreux autres problèmes pratiques avec une précision suffisante.