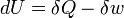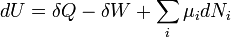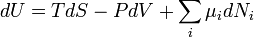Primeira lei da termodinâmica
Informações de fundo
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?
| Leis da termodinâmica |
|---|
| Lei Zero |
| Primeira lei |
| Segunda lei |
| Terceira lei |
| Relação fundamental |
Em termodinâmica , a primeira lei da termodinâmica é uma expressão da lei física mais universal do conservação de energia. Sucintamente, a primeira lei da termodinâmica afirma:
| " | O aumento da energia interna de um sistema é igual à quantidade de energia adicionada pelo aquecimento do sistema, menos a quantidade perdida como resultado do trabalho realizado pelo sistema no seu ambiente. | " |
Descrição
A primeira lei da termodinâmica, basicamente, afirma que um sistema termodinâmico pode armazenar ou manter a energia e que este interna de energia é conservada. O calor é um processo pelo qual a energia é adicionado a um sistema a partir de uma fonte de alta temperatura, ou perdido a uma baixa temperatura afundar. Além disso, a energia pode ser perdida pelo sistema quando ele faz o trabalho mecânico em seu entorno, ou, inversamente, pode ganhar energia como um resultado do trabalho feito sobre ele por seus arredores. A primeira lei estabelece que esta energia é conservada: A variação da energia interna é igual à quantidade adicionada por aquecimento menos a quantidade perdida fazendo o trabalho sobre o meio ambiente. A primeira lei pode ser indicado matematicamente como:
onde 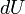 é um pequeno aumento da energia interna do sistema,
é um pequeno aumento da energia interna do sistema, 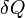 é uma pequena quantidade de calor adicionada ao sistema, e
é uma pequena quantidade de calor adicionada ao sistema, e 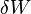 é uma pequena quantidade de trabalho realizado pelo sistema. Como uma analogia, se o calor fosse dinheiro, então poderíamos dizer que qualquer mudança em nossas poupanças (
é uma pequena quantidade de trabalho realizado pelo sistema. Como uma analogia, se o calor fosse dinheiro, então poderíamos dizer que qualquer mudança em nossas poupanças ( 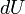 ) É igual ao dinheiro que colocamos no (
) É igual ao dinheiro que colocamos no ( 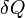 ) Menos o dinheiro que gastamos (
) Menos o dinheiro que gastamos ( 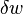 ).
).
Os δ de antes os termos de calor e de trabalho são usados para indicar que eles descrevem um incremento de energia que deve ser interpretado de forma algo diferente do que o incremento dU de energia interna. Trabalho e calor são processos que adicionar ou subtrair de energia, enquanto o U interno da energia é uma forma particular de energia associada com o sistema. Assim, o termo "energia térmica" para 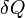 significa "que a quantidade de energia adicionada como o resultado de aquecimento", em vez de se referir a uma forma particular de energia. Da mesma forma, o termo "energia trabalho" para
significa "que a quantidade de energia adicionada como o resultado de aquecimento", em vez de se referir a uma forma particular de energia. Da mesma forma, o termo "energia trabalho" para 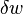 significa "que a quantidade de energia perdida como resultado do trabalho". O resultado mais significativo desta distinção é o fato de que se pode afirmar claramente a quantidade de energia interna possuído por um sistema termodinâmico, mas não se pode dizer quanta energia fluiu para dentro ou para fora do sistema como resultado de seu ser aquecido ou arrefecido , nem como o resultado do trabalho a ser executado em ou através do sistema.
significa "que a quantidade de energia perdida como resultado do trabalho". O resultado mais significativo desta distinção é o fato de que se pode afirmar claramente a quantidade de energia interna possuído por um sistema termodinâmico, mas não se pode dizer quanta energia fluiu para dentro ou para fora do sistema como resultado de seu ser aquecido ou arrefecido , nem como o resultado do trabalho a ser executado em ou através do sistema.
A primeira declaração explícita da primeira lei da termodinâmica foi dada pelo Rudolf Clausius em 1850 : "Não há uma função de estado E, chamado" energia ", cujo diferencial é igual ao trabalho de intercâmbio com os arredores, durante uma processo adiabático. "
Note-se que a formulação acima é favorecido por engenheiros e físicos. Os químicos prefere uma segunda forma, em que o termo trabalho 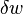 é definida como o trabalho realizado no sistema, e, portanto, inserir um sinal de adição na equação acima, antes do período de trabalho. Este artigo irá utilizar a primeira definição exclusivamente.
é definida como o trabalho realizado no sistema, e, portanto, inserir um sinal de adição na equação acima, antes do período de trabalho. Este artigo irá utilizar a primeira definição exclusivamente.
Formulação matemática
A afirmação matemática da primeira lei é dada por:
onde 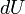 é o aumento infinitesimal da energia interna do sistema,
é o aumento infinitesimal da energia interna do sistema, 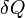 é a quantidade infinitesimal de calor adicionado ao sistema, e
é a quantidade infinitesimal de calor adicionado ao sistema, e 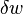 é a quantidade infinitesimal do trabalho realizado pelo sistema. O calor infinitesimal e trabalho são denotados por δ em vez de d, porque, em termos matemáticos, eles não são diferenciais exatas. Em outras palavras, eles não descrevem o estado de todo o sistema. O integral de um diferencial inexacta depende da "via" em particular tomada através do espaço de parâmetros termodinâmicos enquanto que o integrante de um diferencial exato depende apenas os estados iniciais e finais. Se os estados iniciais e finais são os mesmos, então o integrante de um diferencial inexacta pode ou não ser igual a zero, mas o integrante de um diferencial exacta será sempre zero. O caminho tomado por um sistema termodinâmico através do espaço estado é conhecido como um processo termodinâmico.
é a quantidade infinitesimal do trabalho realizado pelo sistema. O calor infinitesimal e trabalho são denotados por δ em vez de d, porque, em termos matemáticos, eles não são diferenciais exatas. Em outras palavras, eles não descrevem o estado de todo o sistema. O integral de um diferencial inexacta depende da "via" em particular tomada através do espaço de parâmetros termodinâmicos enquanto que o integrante de um diferencial exato depende apenas os estados iniciais e finais. Se os estados iniciais e finais são os mesmos, então o integrante de um diferencial inexacta pode ou não ser igual a zero, mas o integrante de um diferencial exacta será sempre zero. O caminho tomado por um sistema termodinâmico através do espaço estado é conhecido como um processo termodinâmico.
Uma expressão da primeira lei pode ser escrito em termos de diferenciais exatas por perceber que o trabalho que um sistema faz é igual às suas pressão vezes a mudança infinitesimal em seu volume. Em outras palavras 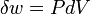 onde
onde 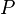 é pressão e
é pressão e 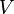 é o volume . Para um processo reversível, a quantidade total de calor adicionado a um sistema pode ser expressa como
é o volume . Para um processo reversível, a quantidade total de calor adicionado a um sistema pode ser expressa como 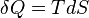 onde
onde 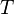 é a temperatura e
é a temperatura e 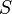 é entropia . Para um processo reversível, a primeira lei pode agora ser reformulada:
é entropia . Para um processo reversível, a primeira lei pode agora ser reformulada:
No caso em que o número de partículas em que o sistema não é necessariamente constante e pode ser de diferentes tipos, a primeira lei está escrito:
onde 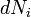 é o (pequeno) número de partículas do tipo I adicionados ao sistema, e
é o (pequeno) número de partículas do tipo I adicionados ao sistema, e 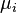 representa a quantidade de energia adicionada ao sistema quando uma partícula do tipo I é adicionado, em que a energia de cada partícula é tal que o volume e a entropia do sistema mantém-se inalterada.
representa a quantidade de energia adicionada ao sistema quando uma partícula do tipo I é adicionado, em que a energia de cada partícula é tal que o volume e a entropia do sistema mantém-se inalterada. 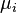 é conhecido como o potencial químico das partículas do tipo I no sistema. A declaração da primeira lei para processos reversíveis, usando diferenciais exatas é agora:
é conhecido como o potencial químico das partículas do tipo I no sistema. A declaração da primeira lei para processos reversíveis, usando diferenciais exatas é agora:
Uma ideia útil da mecânica é que a energia adquirida por uma partícula é igual à força aplicada à partícula multiplicada pelo deslocamento da partícula, enquanto que a força é aplicada. Agora, considere a primeira lei sem o termo de aquecimento: 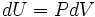 . A pressão P pode ser visto como uma força (e, de facto, tem as unidades de força por unidade de área) enquanto dV é o deslocamento (com unidades de área vezes a distância). Pode-se dizer, no que diz respeito a este período de trabalho, que uma diferença de pressão força uma transferência do volume, e que o produto dos dois (de trabalho) é a quantidade de energia transferida como um resultado do processo.
. A pressão P pode ser visto como uma força (e, de facto, tem as unidades de força por unidade de área) enquanto dV é o deslocamento (com unidades de área vezes a distância). Pode-se dizer, no que diz respeito a este período de trabalho, que uma diferença de pressão força uma transferência do volume, e que o produto dos dois (de trabalho) é a quantidade de energia transferida como um resultado do processo.
É útil para visualizar o termo TdS na mesma luz: No que diz respeito a este termo calor, uma diferença de temperatura força uma transferência de entropia, e o produto dos dois (de calor) é a quantidade de energia transferida como um resultado do processo de . Aqui, a temperatura é conhecida como uma força "generalizada" (ao invés de uma força mecânica efectiva) e a entropia é um deslocamento generalizada.
Do mesmo modo, a diferença do potencial químico entre os grupos de partículas no sistema obriga a uma trasfer de partículas, e o produto correspondente é a quantidade de energia transferida como um resultado do processo. Por exemplo, considere um sistema composto de duas fases: a água líquida e vapor de água. Há uma "força" generalizada de evaporação que conduz moléculas de água para fora do líquido. Há uma "força" generalizada de condensação que acciona as moléculas de vapor para fora do vapor. Somente quando essas duas "forças" (ou potenciais químicos) são iguais haverá equilíbrio, ea transferência líquida será zero.
Os dois parâmetros termodinâmicos que formam um par de f orça-deslocamento generalizada variáveis são denominadas "conjugadas". Os dois pares mais conhecidos são, é claro, pressão-volume e temperatura-entropia.
Tipos de processos termodinâmicos
Caminhos através do espaço de variáveis termodinâmicas são muitas vezes especificado, mantendo certas variáveis termodinâmicas constante. É útil para agrupar estes processos em pares, em que cada variável são mantidas constantes é um membro de um par conjugado.
A par conjugado de pressão-volume está relacionada com a transferência de energia mecânica dinâmica ou como o resultado de trabalho.
- Um processo isobárica ocorre a uma pressão constante. Um exemplo seria ter um pistão móvel num cilindro, de modo que a pressão dentro do cilindro é sempre à pressão atmosférica, embora seja isolada da atmosfera. Em outras palavras, o sistema é ligado de forma dinâmica, por um limite móvel, a um reservatório de pressão constante.
- Um processo isocórica é aquele em que o volume é mantido constante, o que significa que o trabalho realizado pelo sistema será zero. Daqui resulta que, para o sistema simples de duas dimensões, de qualquer energia térmica transferida para o sistema de externamente será absorvida na forma de energia interna. Um processo isocórica também é conhecido como um processo isométrica. Um exemplo seria a de colocar uma lata fechado contendo apenas ar para o fogo. Para uma primeira aproximação, a lata não se expandir, e a única mudança será que o gás ganha energia interna, tal como evidenciado pelo seu aumento de temperatura e pressão. Matematicamente,
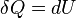 . Pode-se dizer que o sistema é dinamicamente isolados, por um limite rígido, a partir do ambiente
. Pode-se dizer que o sistema é dinamicamente isolados, por um limite rígido, a partir do ambiente
A par conjugado temperatura entropia está preocupado com a transferência de energia térmica, como resultado de aquecimento.
- Um processo isotérmico ocorre a uma temperatura constante. Um exemplo seria a de ter um sistema imersa num grande banho a temperatura constante. Qualquer energia trabalho realizado pelo sistema será perdida para o banho, mas a sua temperatura permanece constante. Em outras palavras, o sistema é ligado termicamente, por um limite termicamente condutora a um reservatório de temperatura constante.
- Um processo isentrópica ocorre a uma entropia constante. Para um processo reversível este é idêntico a um processo adiabático (ver abaixo). Se um sistema tem uma entropia que ainda não atingiu o seu valor máximo de equilíbrio, um processo de arrefecimento pode ser necessário para manter o valor de entropia.
- Um processo adiabático é um processo em que não há energia adicionado ou subtraído do sistema de aquecimento ou de arrefecimento. Para um processo reversível, isto é idêntico a um processo de isentrópica. Pode-se dizer que o sistema está termicamente isolado do seu ambiente e que o seu contorno é um isolante térmico. Se um sistema tem uma entropia que ainda não atingiu o seu valor máximo de equilíbrio, a entropia aumentará mesmo que o sistema é isolado termicamente.
A descrição acima tem todos implicitamente que os limites são também impermeáveis a partículas. Podemos presumir que os limites são rígidas e termicamente isolante, mas são permeáveis a um ou mais tipos de partículas. Considerações semelhantes em seguida, mantenha para o (potencial químico) - (número de partículas) pares conjugados.