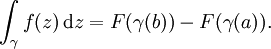Teorema fundamental do cálculo
Informações de fundo
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?
O teorema fundamental do cálculo especifica a relação entre as duas centrais de operações de cálculo , diferenciação e integração .
A primeira parte do teorema, às vezes chamado o primeiro teorema fundamental do cálculo, mostra que um integração indefinido pode ser invertida por uma diferenciação.
A segunda parte, às vezes chamado o segundo teorema fundamental do cálculo, permite calcular a integral definida de uma função usando qualquer um dos seus infinitos antiderivadas. Esta parte do teorema tem aplicações práticas inestimáveis, porque marcadamente simplifica o cálculo de integrais definidas.
A primeira declaração publicada e prova de uma versão restrita do teorema fundamental foi por James Gregory (1638-1675). Isaac Barrow provou a primeira versão completamente geral do teorema, enquanto estudante de Barrow Isaac Newton (1643-1727) completou o desenvolvimento da teoria matemática circundante. Gottfried Leibniz (1646-1716) sistematizaram o conhecimento em um cálculo para as quantidades infinitesimais.
Intuição
Intuitivamente, o teorema indica simplesmente que a soma de variações infinitesimais em uma quantidade ao longo do tempo (ou alguma outra quantidade) somam a mudança líquida na quantidade.
Para compreender esta afirmação, vamos começar com um exemplo. Suponhamos que uma partícula viaja em linha recta com a sua posição dado por x (t) em que t é o tempo e x (t) significa que x é uma função de t. O derivado desta função é igual à variação infinitesimal em quantidade, d x, por variação infinitesimal em tempo, d t (claro, o próprio derivado é dependente do tempo). Vamos definir esta alteração na distância, por mudança no tempo, como a velocidade v da partícula. Em Notação de Leibniz:
Reorganizando a equação, segue-se que:
Pela lógica acima, uma mudança em x ( 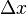 ) É a soma de a alterações infinitesimais d x. Também é igual à soma dos produtos infinitesimais de o derivado e tempo. Esta soma infinita é a integração; Assim, a operação de integração permite a recuperação da função original do seu derivado. Como se pode inferir razoavelmente, esta operação funciona em sentido inverso, como podemos diferenciar o resultado da nossa integrante para recuperar o derivado originais.
) É a soma de a alterações infinitesimais d x. Também é igual à soma dos produtos infinitesimais de o derivado e tempo. Esta soma infinita é a integração; Assim, a operação de integração permite a recuperação da função original do seu derivado. Como se pode inferir razoavelmente, esta operação funciona em sentido inverso, como podemos diferenciar o resultado da nossa integrante para recuperar o derivado originais.
Declarações formais
Há duas partes para o teorema fundamental do cálculo. Frouxamente colocado, as primeira parte trata com o derivado de um antiderivada, enquanto a segunda parte trata da relação entre antiderivadas e integrais definidas .
Primeira parte
Esta parte é por vezes referido como primeiro teorema fundamental do cálculo.
Seja f uma função real contínua definida em um intervalo fechado [a, b]. Seja F a função definida, para todos os x em [a, b], por
Então, F é diferenciável em [a, b], e para cada x em [a, b],
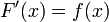 .
.
A operação  é um integral definida com um limite superior variável, e o seu resultado F (x) é um dos muitos infinitamente antiderivadas de f.
é um integral definida com um limite superior variável, e o seu resultado F (x) é um dos muitos infinitamente antiderivadas de f.
Segunda parte
Esta parte é por vezes referido como Segundo Teorema Fundamental do Cálculo.
Seja f uma função real contínua definida em um intervalo fechado [a, b]. Seja F um primitiva de f, que é um dos infinitamente muitas funções de tal modo que, para todos os x em [a, b],
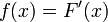 .
.
Em seguida
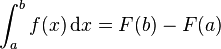 .
.
Corolário
Seja f uma função real definida em um intervalo fechado [a, b]. Seja F uma função tal que, para todo x em [a, b],
Então, para todo x em [a, b],
e
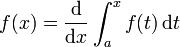 .
.
Exemplos
Como exemplo, suponha que você precisa calcular
Aqui, 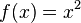 e podemos usar
e podemos usar 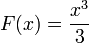 como a antiderivada. Portanto:
como a antiderivada. Portanto:
Ou, de modo mais geral, suponha que você precisa calcular
Aqui, 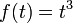 e podemos usar
e podemos usar 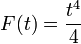 como a antiderivada. Portanto:
como a antiderivada. Portanto:
Mas esse resultado poderia ter sido encontrada mais facilmente como
Prova
Supõe que
Haja dois números x 1 e x 1 + Δ x em [a, b]. Portanto, temos
e
Subtraindo as duas equações dá
Pode ser mostrado que
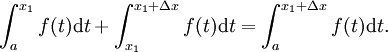
- (A soma das áreas de duas regiões adjacentes é igual à área de ambas as regiões combinadas.)
Manipulando esta equação dá
Substituindo a equação acima em (1) resulta em
De acordo com teorema do valor médio para a integração, existe um c em [x 1, x 1 + x Δ] tal que
 .
.
Substituindo a equação acima em (2) obtemos
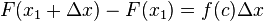 .
.
Dividindo ambos os lados por Δ x dá
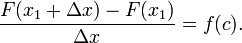
- Note que a expressão no lado esquerdo da equação é a de Newton quociente de diferença para F em x 1.
Tome o limite como x Δ → 0 em ambos os lados da equação.
A expressão do lado esquerdo da equação é a definição do derivado de F em x 1.
Para encontrar o outro limite, usaremos o espremer teorema. O número c está no intervalo [x 1, x 1 + x Δ], então x c 1 ≤ ≤ x 1 + x Δ.
Além disso, 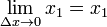 e
e 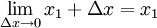 .
.
Portanto, de acordo com o teorema de aperto,
Substituindo em (3), obtemos
A função f é contínua em c, então o limite pode ser tomada dentro da função. Portanto, temos
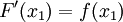 .
.
que completa a prova.
(Leithold et ai, 1996)
Prova alternativa
Esta é uma prova limite por Riemann resume.
Seja f contínua no intervalo [a, b], e seja F uma antiderivada de f. Comece com a quantidade
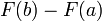 .
.
Haja números
- x 1, ..., x n
tal que
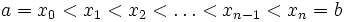 .
.
Segue que
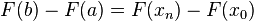 .
.
Agora, podemos adicionar cada F (x i) juntamente com o seu inverso aditivo, de modo a que a quantidade resultante é igual:
A quantidade acima pode ser escrito como a seguinte soma:
Em seguida, vamos empregar o teorema do valor médio. Resumidamente,
Seja F contínua no intervalo fechado [a, b] e diferenciável no intervalo aberto (a, b). Em seguida, existe alguma c em (a, b) de tal modo que
Segue que
A função F é diferenciável no intervalo [a, b]; por conseguinte, também é diferenciável e contínua em cada intervalo de -1 x i. Portanto, de acordo com o teorema do valor médio (acima),
Substituindo a equação acima em (1), obtemos
A suposição implica 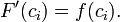 Além disso,
Além disso, 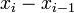 pode ser expresso como
pode ser expresso como 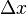 de partição
de partição 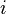 .
.

Observe que estamos descrevendo a área de um retângulo, com os tempos de largura a altura, e estamos adicionando as áreas em conjunto. Cada retângulo, por força da Teorema do Valor Médio, descreve uma aproximação da secção curva que é desenhada sobre. Note também que 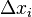 não precisa de ser o mesmo para qualquer valor de
não precisa de ser o mesmo para qualquer valor de 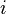 , Ou, em outras palavras, que a largura dos rectângulos podem diferir. O que temos de fazer é aproximar a curva com
, Ou, em outras palavras, que a largura dos rectângulos podem diferir. O que temos de fazer é aproximar a curva com 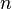 retângulos. Agora, como o tamanho das partições ficar menor e n aumenta, resultando em mais partições para cobrir o espaço, chegaremos mais e mais perto da área real da curva.
retângulos. Agora, como o tamanho das partições ficar menor e n aumenta, resultando em mais partições para cobrir o espaço, chegaremos mais e mais perto da área real da curva.
Ao tomar o limite da expressão como a norma das partições se aproxima de zero, chegamos à Integral de Riemann. Isto é, tomamos o limite como a maior das partições se aproxima de zero em tamanho, de modo que todas as outras partições são menores eo número de partições se aproxima do infinito.
Assim, tomamos o limite em ambos os lados (2). Isto dá-nos
Nem F (b) nem F (a) é dependente || Δ ||, de modo que o limite do lado esquerdo permanece F (b) - F (a).
A expressão no lado direito da equação define uma integral sobre f de a até b. Portanto, obtemos
que completa a prova.
Generalizações
Nós não precisamos assumir a continuidade de f no intervalo todo. Parte I do teorema diz então: Se qualquer f é integrável Lebesgue função em [a, b] e x é um número de 0 a [a, b] tal que f é contínua em x 0, então
é diferenciável para x = x 0 com F '(x 0) = f (x 0). Podemos relaxar as condições de f ainda mais e supor que é apenas localmente integrável. Nesse caso, pode-se concluir que a função F é diferenciável quase todos os lugares e F '(x) = f (x) em quase toda parte. Isso às vezes é conhecido como diferenciação teorema de Lebesgue.
Parte II do teorema é verdadeira para qualquer função integrável Lebesgue f que tem uma antiderivada F (nem todas as funções integráveis fazer, embora).
A versão do teorema de Taylor que expressa o termo de erro como uma integral pode ser visto como uma generalização do teorema fundamental.
Há uma versão do teorema de complexas funções: suponha que U é um conjunto aberto em C ef: U → C é uma função que tem um F antiderivative holomorfa em U. Então para cada curva γ: [a, b] → U, o curva integral pode ser calculado como
O teorema fundamental pode ser generalizado para curvas e superfícies integrais em dimensões superiores e em manifolds .
Uma das declarações mais poderosas nessa direção é Teorema de Stokes.

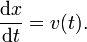
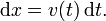
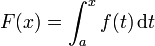
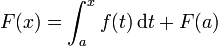
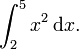
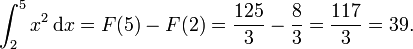
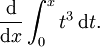
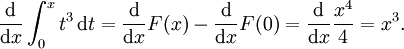
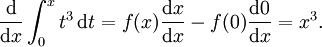
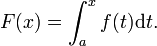
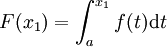
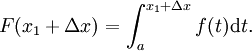
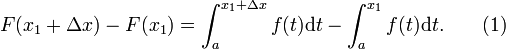

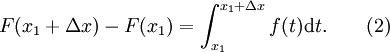
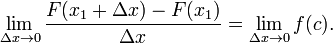
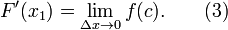
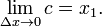
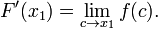
![\ Begin {matriz} F (b) - F (a) & = & F (x_n) \, + \, [- F (x_ {n-1}) \, + \, F (x_ {1} n- )] \, + \, \ ldots \, + \, [- F (x_1) + F (x_1)] \, - \, F (x_0) \, \\ & = & [F (x_n) \, - \, F (x_ {n-1})] \, + \, [F (x_ {n-1}) \, + \, \ ldots \, - \, F (x_1)] \, + \, [ F (x_1) \ - \, F (x_0)] \, \ end {matrix}](../../images/62/6206.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [F (x_i) - F (x_ {} i-1)] \ qquad (1)](../../images/62/6207.png)
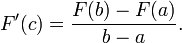
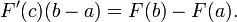
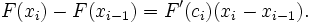
![F (b) - F (a) = \ sum_ {i = 1} ^ N [F '(C_I) (x_i - x_ {} i-1)].](../../images/62/6211.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [f (C_I) (\ Delta x_i)] \ qquad (2)](../../images/62/6215.png)
![\ Lim _ {\ | \ Delta \ | \ to 0} F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ to 0} \ sum_ {i = 1} ^ n [f (C_I) (\ Delta x_i)] \ ,.](../../images/62/6225.png)
![F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ to 0} \ sum_ {i = 1} ^ n [f (C_I) (\ Delta x_i)]](../../images/62/6226.png)