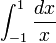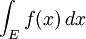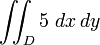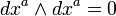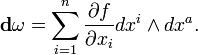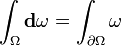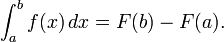Integral
Fundo para as escolas Wikipédia
Esta seleção wikipedia foi escolhido por voluntários que ajudam Crianças SOS da Wikipedia para este Seleção Wikipedia para as escolas. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
- A palavra "integral" (adjetivo) também pode significar: "ser um número inteiro ".
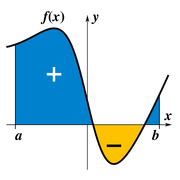
A integração é um conceito central da avançados matemática , especificamente nas áreas de cálculo e análise matemática . Dada uma função f (x) de uma verdadeira x e uma variável intervalo [a, b] da linha real, o integrante
é igual à área de uma região no -plane xy delimitada pela gráfico de f, o eixo x, e a vertical linhas x = a e x = b, com áreas abaixo do eixo x sendo subtraído.
O termo "integral" também pode se referir à noção de antiderivada, uma função F cujo derivado é a função dada f. Neste caso, ele é chamado de integral indefinida, enquanto as integrais discutidos neste artigo são denominados integrais definidas. Alguns autores manter uma distinção entre antiderivadas e integrais indefinidas.
Os princípios de integração foram formuladas por Isaac Newton e Gottfried Leibniz no final do século XVII. Através do teorema fundamental do cálculo , que eles desenvolveram de forma independente, a integração está conectado com diferenciação, e o integral definida de uma função pode ser facilmente calculado uma vez que uma primitiva é conhecido. Integrais e derivados tornaram-se as ferramentas básicas de cálculo , com numerosas aplicações em ciência e engenharia.
Uma definição matemática rigorosa da integral foi dada por Bernhard Riemann . Ele baseia-se numa limitação procedimento que se aproxima da área de uma região curvilínea, quebrando a região em lajes finas verticais. A partir do século XIX, noções mais sofisticadas de integrante começaram a aparecer, onde o tipo de função, bem como o domínio sobre o qual se realiza a integração tem sido generalizada. A A linha integral é definido para as funções de duas ou três variáveis, e o intervalo de integração [a, b] é substituído por uma certa curva de ligação entre dois pontos no plano ou no espaço. Em um integral de superfície, a curva é substituída por uma peça de um superfície no espaço tridimensional. Integrais de formas diferenciais desempenhar um papel fundamental na moderna geometria diferencial . Essas generalizações de integrante primeiro surgiu das necessidades de física , e eles têm um papel importante na formulação de muitas leis físicas, notadamente os de eletrodinâmica. Os conceitos modernos de integração são baseados na teoria matemática conhecida como resumo integração Lebesgue , desenvolvido pela Henri Lebesgue.
História
Pré-cálculo de integração
A integração pode ser rastreada tanto para trás como o antigo Egito, por volta de 1800 aC, com a Moscovo papiro matemático demonstrando conhecimento de uma fórmula para o volume de um piramidal tronco. A técnica sistemática documentada pela primeira vez capaz de integrais determinante é a método de esgotamento de Eudoxus (circa 370 aC), que procurou encontrar áreas e volumes, quebrando-se em um número infinito de formas para que a área ou volume era conhecido. Este método foi adicionalmente desenvolvido e utilizado pela Arquimedes e usadas para calcular as áreas de parábolas e uma aproximação à área de um círculo. Métodos semelhantes foram desenvolvidos de forma independente na China por volta do século 3 dC por Liu Hui, que o usou para encontrar a área do círculo. Este método foi usado mais tarde por Zu Chongzhi para calcular o volume de uma esfera. Algumas idéias do cálculo integral são encontrados no Siddhanta Shiromani, um 12o texto astronomia século pelo matemático indiano Bhaskara II.
Avanços significativos na técnicas como o método da exaustão não começam a aparecer até o século 16 dC. Neste momento, o trabalho de Cavalieri com o seu método dos indivisíveis, e trabalho por Fermat , começou a lançar as bases de cálculo moderno. Novas medidas foram feitas no início do século 17 por Barrow e Torricelli, que forneceu os primeiros sinais de uma conexão entre a integração e diferenciação.
Newton e Leibniz
O grande avanço na integração veio no século 17 com a descoberta independente do teorema fundamental do cálculo por Newton e Leibniz . O teorema demonstra uma conexão entre integração e diferenciação. Esta ligação, combinada com a facilidade comparativa de diferenciação, podem ser exploradas para calcular integrais. Em particular, o teorema fundamental do cálculo permite resolver uma classe muito maior de problemas. De igual importância é a estrutura matemática abrangente que Newton e Leibniz desenvolveram. Dado o nome de cálculo infinitesimal, permitiu análise precisa das funções dentro de domínios contínuos. Este quadro se tornou moderno Cálculo , cuja notação para integrais é tirado diretamente do trabalho de Leibniz.
Formalizando integrais
Enquanto Newton e Leibniz fornecida uma abordagem sistemática para a integração, o seu trabalho não tinha um grau de rigor. Bishop Berkeley memoravelmente atacado infinitesimais como "os fantasmas da quantidade partiu". Cálculo adquiriu uma base mais firme com o desenvolvimento de limites e foi dada uma base adequada por Cauchy na primeira metade do século 19. Integração foi primeiro rigorosamente formalizado, utilizando limites, por Riemann . Apesar de tudo por partes limitada funções contínuas são Riemann integrável em um intervalo limitado, posteriormente, as funções mais gerais foram consideradas, para o qual a definição de Riemann não se aplica, e Lebesgue formulou uma definição diferente de integral, fundada em teoria da medida. Outras definições de integrante, estendendo-se abordagens de Riemann e Lebesgue das, foram propostas.
Notação
Isaac Newton usou uma pequena barra vertical acima de uma variável para indicar integração, ou colocado a variável dentro de uma caixa. A barra vertical foi facilmente confundido com 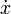 ou
ou 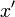 , Que Newton usado para indicar a diferenciação, ea notação caixa era difícil para impressoras de reproduzir, de modo que essas notações não foram amplamente adotadas.
, Que Newton usado para indicar a diferenciação, ea notação caixa era difícil para impressoras de reproduzir, de modo que essas notações não foram amplamente adotadas.
A notação moderna para a integral indefinida foi introduzido por Gottfried Leibniz em 1675 (Burton 1988, p 359;. Leibniz 1899, 154 p.). Adaptou o símbolo integrante, "∫", a partir de um letra S alongada, estando para summa (latim para "soma" ou "total"). A notação moderna para a integral definida, com limites acima e abaixo do sinal de integral, foi usado pela primeira vez por Joseph Fourier em Mémoires da Academia Francesa em torno de 1819-1820, reimpresso em seu livro de 1822 (Cajori 1929, pp 249-250;. Fourier 1822, §231). Em Notação matemática árabe, que é escrito da direita para a esquerda, um símbolo integrante invertido 22px é usado (W3C 2006).
Terminologia e notação
Se uma função tem uma parte integrante, que se diz ser integrável. A função para a qual é calculado o integral é chamado o integrando. A região sobre a qual uma função está sendo integrado é chamado de domínio de integração. Se o integral não tem um domínio de integração, é considerada indefinida (uma com um domínio é considerada definitiva). Em geral, o integrando pode ser uma função de mais de uma variável, e o domínio de integração pode ser uma área, o volume, uma região de elevada dimensão, ou até mesmo um espaço de resumo que não têm uma estrutura geométrica em qualquer sentido usual.
O caso mais simples, o integral de uma função de valor real de uma variável de f x real no intervalo [a, b], é denotada por
O sinal ∫, um "S" alongado, representa integração; a e b são o limite inferior e um limite superior de integração, que define o domínio de integração; f é o integrando, de ser avaliadas quanto x varia ao longo do intervalo [a, b ]; dx e pode ter diferentes interpretações, dependendo da teoria a ser utilizado. Por exemplo, ele pode ser visto como simplesmente uma notação indica que x é o 'dummy' de integração, como um reflexo dos pesos na soma de Riemann, uma medida (em integração de Lebesgue e suas extensões), um infinitesimal (em não análise -padrão) ou como uma quantidade matemática independente: um forma diferencial. Casos mais complicados podem variar a notação ligeiramente.
Introdução
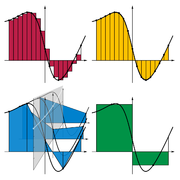
Integrais aparecem em muitas situações práticas. Considere-se uma piscina. Se for rectangular, em seguida, a partir do seu comprimento, largura e profundidade que pode facilmente determinar o volume de água que pode conter (para enchê-lo), a área da sua superfície (a cobri-lo), e o comprimento do seu bordo (a corda-lo). Mas se for oval com um fundo arredondado, todas estas quantidades pedem integrais. Aproximações práticas pode ser suficiente no início, mas eventualmente nós exigimos respostas exatas e rigorosos para tais problemas.

Para começar, considere a curva y = f (x) entre x = 0 e x = 1, com f (x) = x √. Perguntamos:
- O que é a área sob a função f, no intervalo de 0 a 1?
e chamam esta área (ainda desconhecido) a integral de f. A notação para esta integral será
Como uma primeira aproximação, olhar para a unidade quadrada dada pelos lados x = 0 e x = 1 e y = f (0) = 0 e y = f (1) = 1. A sua área é exactamente 1. Como é, o verdadeiro valor do integral tem de ser um pouco menos. Diminuindo a largura dos retângulos de aproximação deve dar um resultado melhor; assim atravessar o intervalo em cinco passos, utilizando os pontos de aproximação 0, 1/5, 2/5, e assim por diante para 1. Montar uma caixa para cada passo utilizando a altura da extremidade direita de cada peça curva, assim √ 1/5, √ 2/5, e assim por diante para √1 = 1. Somando as áreas desses retângulos, obtemos uma melhor aproximação para a integral procurado, ou seja,
Observe que nós estamos tendo uma soma de um número finito de valores da função de f, multiplicados com as diferenças de dois pontos de aproximação subsequentes. Podemos facilmente ver que a aproximação é ainda muito grande. Usando mais etapas produz uma maior aproximação, mas nunca vai ser exato: a substituição dos cinco subintervalos por doze como representado, teremos um valor aproximado para a área de 0,6203, o que é muito pequeno. A ideia-chave é a transição da adição de um número finito de diferenças de pontos de aproximação multiplicados pelos seus respectivos valores da função para usar infinitamente multa, ou passos infinitesimais.
Como para o cálculo real de integrais, o teorema fundamental do cálculo , devido a Newton e Leibniz, é o elo fundamental entre as operações de diferenciação e integração. Aplicado à curva raiz quadrada, f (x) = x 1/2, ele diz para olhar a função relacionada F (x) = 2/3 x 3/2, e simplesmente tomar F (1) - F (0) , onde 0 e 1 são os limites da intervalo [0,1]. (Este é um exemplo de uma regra geral, que para f (x) = x q, sendo q ≠ -1, a função relacionada, a chamada primitiva é F (x) = (x 1 Q) / (q + 1).) Assim, o valor exacto da área sob a curva é calculada como formalmente
A notação
concebe o integral como uma soma ponderada, denotada pelo alongado "S", com os valores da função, f (x), multiplicado por larguras passo infinitesimais, os chamados diferenciais, denotada por dx. O sinal de multiplicação é geralmente omitido.
Historicamente, após o fracasso dos esforços iniciais para interpretar rigorosamente infinitesimais, Riemann integrais definidas formalmente como um limite de somas ponderadas, de modo que o dx sugeriu o limite de uma diferença (ou seja, a largura do intervalo). Deficiências da dependência de Riemann em intervalos ea continuidade motivado definições mais recentes, especialmente a integral de Lebesgue , que se baseia em uma capacidade de estender a idéia de "medida" de maneiras muito mais flexíveis. Assim, a notação
refere-se a uma soma ponderada, em que os valores da função são divididas, com μ medindo o peso a ser atribuído a cada valor. Aqui A indica a região de integração.
Geometria diferencial , com o seu "cálculo em manifolds ", dá a notação familiarizado ainda uma outra interpretação. Agora f (x) dx e tornar-se um forma diferencial, ω = f (x) dx, um novo d operador diferencial, conhecido como o exterior derivado aparece, eo teorema fundamental torna-se o mais geral Teorema de Stokes,
do qual Teorema de Green, o teorema da divergência, eo teorema fundamental do cálculo acompanhamento.
Mais recentemente, infinitesimais reapareceram com rigor, através de inovações modernas, tais como análise não-padrão. Não só estes métodos reivindicar as intuições dos pioneiros, eles também levar a novas matemática.
Embora existam diferenças entre essas concepções de integral, há uma sobreposição considerável. Assim, a área da superfície da piscina oval pode ser tratada como uma elipse geométrica, como uma soma de infinitesimais, como um integral de Riemann, como um Lebesgue, ou como um bloco com uma forma diferencial. O resultado será calculado o mesmo para todos.
Definições formais
Há muitas maneiras de formalmente definindo uma integral, dos quais nem todos são equivalentes. As diferenças existem principalmente para lidar com diferentes casos especiais que não podem ser integrável ao abrigo de outras definições, mas também, ocasionalmente, por razões pedagógicas. As definições mais comumente usados de integral são integrais de Riemann e integrais de Lebesgue.
Integral de Riemann

O integral de Riemann é definido em termos de Somas de Riemann de funções no que diz respeito a partições com a tag de um intervalo. Deixe [a, b] ser um intervalo fechado da linha real; em seguida, uma partição com etiquetas de [a, b] é uma sequência finita
Este particiona o intervalo [a, b] em sub-intervalos i [i x -1, x i], cada um dos quais é "marcado" com um ponto distinto t i ∈ [x i -1, x i]. Vamos Δ i = x i - i x -1 ser a largura do intervalo de sub-i; em seguida, a malha de uma tal partição com etiquetas é a largura da maior sub-intervalo formado pela divisória, max i = 1 ... n Δ i. A soma de Riemann de uma função f, com respeito a uma tal partição marcado for definido como
Assim, cada termo da soma é a área de um rectângulo com a altura igual ao valor da função no ponto distinto do dado sub-intervalo, e a mesma largura como a largura da sub-intervalo. O integral de Riemann de uma função f no intervalo [a, b] é igual a S se:
- Para todos ε> 0 existe δ> 0 tal que, para qualquer partição marcou [a, b] com malha inferior a δ, temos
Quando as balizas dar o máximo (respectivamente, no mínimo) valor de cada intervalo, a soma de Riemann torna-se uma parte superior (respectivamente, inferior) Soma Darboux, sugerindo a estreita ligação entre a integral de Riemann eo Darboux integral.
Lebesgue
O integral de Riemann não é definida por uma vasta gama de funções e situações de importância em aplicações (e de interesse em teoria). Por exemplo, o integral de Riemann pode facilmente integrar densidade para encontrar a massa de uma viga de aço, mas não pode acomodar uma esfera de aço que descansa sobre ele. Isso motiva outras definições, em que uma variedade mais ampla de funções é integrável (Rudin, 1987). A integral de Lebesgue, em particular, alcança grande flexibilidade, direcionando a atenção para os pesos na soma ponderada.
A definição do integral de Lebesgue começa, assim, com um medida, μ. No caso mais simples, o Lebesgue μ (A) de um intervalo A = [a, b] é a sua largura, b - uma, de modo que o integral de Lebesgue concorda com o (adequado) integral de Riemann quando ambos existem. Em casos mais complicados, os conjuntos sendo medidos podem ser altamente fragmentada, sem continuidade e qualquer semelhança com intervalos.
Para explorar essa flexibilidade, integrais de Lebesgue reverter a abordagem à soma ponderada. Como Folland (1984, p. 56) coloca, "Para calcular a integral de Riemann de f, uma partições do domínio [a, b] em subintervalos", enquanto no Lebesgue integral ", uma está em vigor particionar o intervalo de f ".
Uma abordagem comum define o primeiro integrante do função de indicador de um Um conjunto mensurável por:
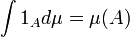 .
.
Isso se estende por linearidade de um mensurável função simples s, que alcança apenas um número finito, n, dos valores não-negativos distintas:
(Onde a imagem de um i sob a função simples s é o valor constante a i). Assim, se E é um conjunto mensurável se define
Então para qualquer não-negativo função mensurável f se define
isto é, o integral da f é definido para ser a supremo de todos os integrais de funções simples que são menos do que ou igual a f. Um geral mensurável função f, é dividido em seus valores positivos e negativos, definindo
Finalmente, f é Lebesgue integrável se
e, em seguida, a integral é definida pela
Quando o espaço medida em que as funções são definidas é também um localmente compacto espaço topológico (como é o caso com os números reais R), mede compatível com a topologia num sentido adequado ( Medidas de radão, dos quais a medida de Lebesgue é um exemplo) e integral com respeito a eles podem ser definidos de forma diferente, a partir dos integrais de funções contínuas com suporte compacto. Mais precisamente, as funções de suporte compacta formar um espaço vector que transporta um naturais topologia, e um (Radon) medida pode ser definida como qualquer contínua linear funcional neste espaço; o valor de uma medida em função de uma forma compacta, em seguida, também é suportada por definição, o integral da função. Uma então começa a expandir a medida (a integral) para funções mais gerais pela continuidade, e define a medida de um conjunto como o integrante da sua função de indicador. Esta é a abordagem adoptada pela Bourbaki (2004) e um certo número de outros autores. Para mais detalhes veja Medidas de radônio.
Outros integrais
Embora os integrais Riemann e Lebesgue são as definições mais importantes do integrante, um número de outros existem, incluindo:
- O Riemann-Stieltjes integral, uma extensão da integral de Riemann.
- O Lebesgue-Stieltjes integral, desenvolvido por Johann Radon, que generaliza o Riemann-Stieltjes e Lebesgue integrais .
- O Daniell integral, que subsume o integral de Lebesgue e Lebesgue-Stieltjes integrante sem a dependência de medidas.
- O Henstock-Kurzweil integral, definido de várias maneiras por Arnaud Denjoy, Oskar Perron, e (mais elegante, como o medidor integrante) Jaroslav Kurzweil, e desenvolvido por Ralph Henstock.
Propriedades de integração
Linearidade
- A colecção de funções Riemann integrável em um intervalo fechado [a, b] forma um espaço vectorial de acordo com as operações de adição e multiplicação pontual por um escalar, e a operação de integração
- é um linear funcional neste espaço vectorial. Assim, em primeiro lugar, a coleção de funções integráveis é fechado sob tomada combinações lineares; e, por outro lado, a integral de uma combinação linear é a combinação linear dos integrais,
- Da mesma forma, o conjunto de reais -valued Lebesgue funções integráveis em um determinado E medida espaço com medida μ é fechado sob tomando combinações lineares e, portanto, formam um espaço vetorial e integral de Lebesgue
- é uma cadeia linear funcional neste espaço vectorial, de modo que
- De modo mais geral, considerar o espaço vectorial de todos funções mensuráveis em um espaço de medida (E μ,), tomando valores em um localmente compacto completo topológico espaço vetorial V sobre um compacto localmente topológica K campo, f: E → V. Em seguida, pode-se definir um mapa integração abstrato atribuindo a cada função f um elemento de V ou o símbolo ∞,
- que seja compatível com as combinações lineares. Nesta situação, a linearidade é válido para o subespaço de funções cujo integral é um elemento de V (ou seja, "finito"). Os casos mais importantes especiais surgem quando K é R, C, ou uma extensão finita do campo Q p de números p-adic, e V é um espaço vectorial de dimensão finita sobre K, e quando K = C e V é um complexo Espaço de Hilbert.
Linearidade, em conjunto com algumas propriedades de continuidade naturais e normalização para uma determinada classe de funções de "simples", pode ser usado para dar uma definição alternativa do integral. Esta é a abordagem de Daniell para o caso de funções reais em um conjunto X, generalizada por Nicolas Bourbaki para funções com valores em um espaço localmente compacto topológica vetor. Ver (Hildebrandt 1953) para uma caracterização axiomática da integral.
Desigualdades para integrais
Uma série de desigualdades gerais segure por Riemann-integráveis funções definidas em um e fechado delimitada intervalo [a, b] e pode ser generalizada para outras noções de integral (de Lebesgue e Daniell).
- Limites superior e inferior. Uma função f integrável em [a, b], é necessariamente delimitada em que intervalo. Assim, há números reais m e M para que m ≤ f (x) ≤ M para todo x em [a, b]. Uma vez que os montantes inferiores e superiores de f em [a, b] são, por conseguinte, limitado por, respectivamente, m (b - a) e M (b - a), segue-se que
- As desigualdades entre funções. Se f (x) ≤ g (x) para cada x [a, b] em seguida, cada um dos montantes superiores e inferiores de f é limitada superiormente pelas somas superiores e inferiores, respectivamente, de g. Assim
- Esta é uma generalização das desigualdades acima, como M (b - a) é o integral da função constante com o valor de M em [a, b].
- Subintervalos. Se [c, d] é um subintervalo de [a, b] e f (x) é não-negativo para todos os x e depois
- Produtos e valores absolutos de funções. Se f e g são duas funções, em seguida, nós pode considerar sua produtos pontuais e poderes, e valores absolutos :
- Se f for Riemann integrável em [a, b] em seguida, o mesmo é verdadeiro para | f | e
- Além disso, se f e g são ambos Riemann integrável então f 2, 2 g, e fg são também Riemann integrável, e
- Essa desigualdade, conhecido como o Desigualdade de Cauchy-Schwarz, desempenha um papel de destaque na Teoria do espaço de Hilbert, onde o lado esquerdo é interpretado como o produto interno de duas funções quadrado-integrável F e G no intervalo [a, b].
- A desigualdade de Hölder. Suponha que p e q são dois números reais, 1 ≤ p, q ≤ ∞ com 1 / p + 1 / q = 1, e f e g são duas funções Riemann-integráveis. Em seguida, o funções | f | p e | g | q também são integráveis ea seguinte A desigualdade de Hölder detém:
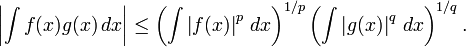
- Para p = q = 2, a desigualdade de Hölder torna-se a desigualdade de Cauchy-Schwarz.
- Desigualdade de Minkowski. Suponha que p ≥ 1 é um número real e f e g são funções Riemann-integráveis. Então | f | p, | g | p e | f + g | p são também Riemann integrável ea seguinte Desigualdade de Minkowski detém:
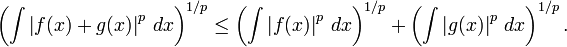
- Um análogo de desigualdade para este Lebesgue é usado na construção de L espaços pág.
Convenções
Nesta secção f é uma de valor real Riemann integrável função . A integral
durante um intervalo [a, b] é definida se a <b. Isto significa que os montantes superiores e inferiores da função f são avaliadas numa partição a = 0 x 1 x ≤ ≤. . . ≤ x n = b cujos valores x i estão a aumentar. Geometricamente, isso significa que a integração ocorre "esquerda para a direita", avaliando f dentro de intervalos [x i, x i 1], onde um intervalo com um índice mais elevado encontra-se ao direito de um com um índice mais baixo. Os valores de a e b, os pontos finais da intervalo, são chamados a limites de integração de f. Integrais também pode ser definida, se a> b;
- Invertendo limites de integração. Se a> b, em seguida, definir
Este, com a = b, implica:
- Integrais sobre intervalos de comprimento zero. Se um é um número real , em seguida,
A primeira convenção é necessária tendo em consideração a tomar integrais sobre subintervalos de [a, b]; a segunda diz que tomou uma integral sobre um intervalo degenerado, ou um ponto, deve ser de zero . Uma das razões para a primeira convenção é que a integrabilidade de f no intervalo [a, b] implica que f é integrável em qualquer subintervalo [c, d], mas em especial os integrais têm a propriedade de que:
- Aditividade de integração em intervalos. Se c é qualquer elemento, [, b a], em seguida,
Com a primeira convenção a relação resultante
é então bem definidos para qualquer permutação cíclica de a, b, e c.
Em vez de ver o acima como convenções, também se pode adotar o ponto de vista de que a integração é realizada em manifolds orientadas somente. Se M é uma variedade M-dimensional orientada tal, e M 'é o mesmo bloco com orientação oposta e ω é uma m -forma, então um tem (veja abaixo a integração de formas diferenciais):
Teorema fundamental do cálculo
O teorema fundamental do cálculo é a afirmação de que a diferenciação e integração são operações inversas: se um função contínua é primeiramente integrada e depois diferenciada, a função original será recuperada. Uma consequência importante, às vezes chamado o segundo teorema fundamental do cálculo, permite computar integrais utilizando um antiderivada da função a ser integrada.
As declarações de teoremas
- Teorema fundamental do cálculo. Seja f uma de valor real integrável função definida em um intervalo fechado [a, b]. Se F é definida para x em [a, b] por
- F é então contínua em [a, b]. Se f é contínua em x em [a, b], então M é diferenciável em x, e F '(x) = f (x).
- Segundo teorema fundamental do cálculo. Seja f uma função integrável reais definidas em um intervalo fechado [a, b]. Se F é uma função tal que F '(x) = f (x) para todos os x em [a, b] (isto é, M é um primitiva de f), então
- Corolário. Se f é uma função contínua em [a, b], então f é integrável em [a, b], e F, definido pela
- é um anti-derivado de f em [a, b]. Além disso,
Extensões
Integrais impróprias
Um "bom" integral de Riemann assume o integrando é definido e finito em um intervalo fechado e limitado, suportadas pelos limites de integração. Uma integral imprópria ocorre quando uma ou mais destas condições não está satisfeita. Em alguns casos, tais integrais podem ser definidas tendo em consideração o limite de uma sequência adequada de Riemann integrais em intervalos cada vez maiores.
Se o intervalo é ilimitado, por exemplo na sua extremidade superior, em seguida, o integral imprópria é o limite como ponto final que vai para infinito.
Se o integrando é apenas definida ou finita sobre um intervalo semi-aberto, por exemplo (a, b], em seguida, novamente um limite pode proporcionar um resultado finito.
Ou seja, a integral imprópria é o limite de integrais adequadas como um ponto final do intervalo da integração aproxima ou um determinado número real , ou ∞, ou -∞. Em casos mais complicados, os limites são necessários em ambas as extremidades, ou em pontos interiores.
Considere-se, por exemplo, a função 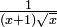 integrada de 0 a ∞ (mostrado à direita). No limite inferior, como x vai para 0 a função vai para ∞, e o limite superior é em si ∞, embora a função vai para 0. Assim, este é um duplamente integral imprópria. Integrado, por exemplo, de 1 a 3, uma soma de Riemann ordinário é suficiente para produzir um resultado de
integrada de 0 a ∞ (mostrado à direita). No limite inferior, como x vai para 0 a função vai para ∞, e o limite superior é em si ∞, embora a função vai para 0. Assim, este é um duplamente integral imprópria. Integrado, por exemplo, de 1 a 3, uma soma de Riemann ordinário é suficiente para produzir um resultado de 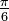 . Para integrar de 1 a ∞, uma soma de Riemann não é possível. No entanto, qualquer finito limite superior, dizer t (com t> 1), dá um resultado bem definido,
. Para integrar de 1 a ∞, uma soma de Riemann não é possível. No entanto, qualquer finito limite superior, dizer t (com t> 1), dá um resultado bem definido, 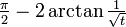 . Isto tem um limite finito como t tende para infinito, nomeadamente
. Isto tem um limite finito como t tende para infinito, nomeadamente  . Da mesma forma, a integral a partir de 1/3 para 1 permite uma soma de Riemann assim, coincidentemente novamente produzindo
. Da mesma forma, a integral a partir de 1/3 para 1 permite uma soma de Riemann assim, coincidentemente novamente produzindo 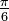 . Substituir 1/3 por um valor positivo arbitrário s (com s <1) é igualmente segura, dando
. Substituir 1/3 por um valor positivo arbitrário s (com s <1) é igualmente segura, dando 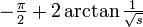 . Isto, também, tem um limite finito como s for igual a zero, ou seja
. Isto, também, tem um limite finito como s for igual a zero, ou seja  . Combinando os limites dos dois fragmentos, o resultado desta integral é inadequada
. Combinando os limites dos dois fragmentos, o resultado desta integral é inadequada
Este processo não é sucesso garantido; um limite pode não existir, ou podem ser ilimitado. Por exemplo, durante o intervalo limitado 0-1 o integral de 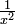 não converge; e ao longo do intervalo de 1 a infinito ∞ o integral de
não converge; e ao longo do intervalo de 1 a infinito ∞ o integral de 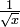 não converge.
não converge.
Também pode acontecer que um integrando é ilimitado a um ponto interior, caso em que o integral deve ser dividida neste ponto, e devem existir os integrais limite de ambos os lados e tem de ser limitada. Assim
Mas o integral semelhante
não pode ser atribuído um valor, desta forma, como os integrais acima e abaixo de zero não convergem de forma independente. (No entanto, ver Cauchy valor do principal.)
Integração múltipla
Integrais podem ser tomadas em relação a outras regiões do que intervalos. Em geral, um integrante ao longo de um conjunto E de uma função f está escrito:
Aqui x não precisa de ser um número real, mas pode ser uma outra quantidade adequada, por exemplo, um vector em R 3 . teorema de Fubini mostra que essas integrais pode ser reescrita como um integrante iterado . Em outras palavras, a integral pode ser calculada integrando uma coordenada de cada vez.
Assim como o integral definida de uma função positiva de uma variável representa aáreada região entre o gráfico da função e ox-axis, ointegral duplade uma função de duas variáveis positivo representa ovolume doda região entre a superfície definida por a função e o plano que contém o seu domínio.(O mesmo volume pode ser obtida através datripla integrante- o integral de uma função em três variáveis - de a função da constantede f(x,y,z) = 1 sobre a região acima mencionada entre a superfície e o plano.) Se o número de variáveis é maior, então a integral representa umhipervolume, um volume de um sólido de mais de três dimensões que não podem ser representadas graficamente.
Por exemplo, o volume doparalelepípedo de lados de 4 x 6 x 5 pode ser obtido de duas maneiras:
- Pelo integral duplo
- da funçãof(x,y) = 5 calculada na regiãoDnaxy-plane que é a base do paralelipípedo.
- Pela integral triplo
- da função constante 1, calculado sobre o próprio paralelepípedo.
Porque é impossível calcular oantiderivada de uma função de mais de uma variável,indefinidaintegrais múltiplas não existem, por isso tais integrais são todosdefinitiva.
Integrais de linha
O conceito de uma integral pode ser alargado a domínios mais gerais de integração, tais como linhas curvas e superfícies. Tais integrais são conhecidos como integrais de linha e integrais de superfície, respectivamente. Estes têm importantes aplicações na física, como quando se lida com campos de vetores.
Uma linha integrante (por vezes chamado um caminho integral ) é um integral, onde a função a ser integrada é avaliada ao longo de uma curva . Vários integrais de linha diferentes estiverem em uso. No caso de uma curva fechada, é também chamado um contorno integrante .
A função a ser integrada pode ser um campo escalar ou um campo vetorial. O valor do integral de linha é a soma dos valores de campo em todos os pontos na curva, ponderado por uma função escalar na curva (geralmente de comprimento de arco ou, para um vetor campo, o produto escalar do vector de campo com um vector diferencial na curva). Essa ponderação distingue a integral de linha de integrais simples definidas em intervalos. Muitas fórmulas simples de física têm análogos contínuos naturais em termos de integrais de linha; por exemplo, o facto de que o trabalho é igual a forçar multiplicado pela distância pode ser expressa (em termos de quantidades vector) como:
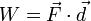 ;
;
que é paralelo com a integral de linha:
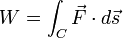 ;
;
que resume os componentes do vetor ao longo de um caminho contínuo e, assim, encontra o trabalho feito em um objeto que se move através de um campo, como um campo elétrico ou gravitacional
Integrais de superfície
Um integral de superfície é um integral definida tomadas ao longo de um superfície (que pode ser uma curva no conjunto espaço); que pode ser pensado como o análogo integrante duplo da linha integral. A função a ser integrada pode ser um campo escalar ou um campo vetorial. O valor do integral de superfície é a soma do campo em todos os pontos na superfície. Isto pode ser conseguido pela divisão da superfície para elementos de superfície, que fornecem o particionamento de somas de Riemann.
Para um exemplo de aplicações de integrais de superfície, considere um campo vetorial v sobre uma superfície S ; isto é, para cada ponto x em S , v ( x ) é um vector. Imagine que temos um fluido que se escoa através de S , de modo a que v ( x ) determina a velocidade do fluido a x . O de fluxo é definida como a quantidade de fluido que flui através de S em quantidade unidade de tempo. Para encontrar o fluxo, nós precisamos de tomar o produto do ponto de v com a unidade de superfície normal a S em cada ponto, o que nos dará um campo escalar, o que podemos integrar sobre a superfície:
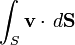 .
.
O fluxo de fluido neste exemplo pode ser a partir de um fluido física, tais como água ou ar, ou a partir do fluxo eléctrico ou magnético. Assim integrais de superfície têm aplicações em física , particularmente com a teoria clássica do eletromagnetismo .
Integrais de formas diferenciais
A forma diferencial é um conceito matemático nas áreas decálculo multivariada,topologia diferencial e tensores.A notação moderna para a forma diferencial, assim como a idéia das formas diferenciais como sendo osprodutos de cunha dederivados exteriores que formam umálgebra exterior, foi introduzido por Élie Cartan.
Nós inicialmente trabalhar em um conjunto aberto em R n . A 0-forma é definida como sendo uma função suave f . Quando integramos uma função f sobre um m - dimensional subespaço S de R n , nós escrevê-lo como
(Os expoentes são índices, não expoentes.) Podemos considerar dx 1 através dx n ser próprios objetos formais, ao invés de etiquetas anexas para fazer integrais olhar como Riemann resume. alternativa, podemos vê-los como covectors, e, portanto, uma medida de "densidade" (daí integrável em um sentido geral). Chamamos a dx 1 , ..., dx n básicos 1- formas .
Nós definimos oproduto cunha, "∧", um operador bilinear "multiplicação" sobre estes elementos, com aalternânciapropriedade que
para todos os índices de um . Note-se que a alternância juntamente com linearidade implica dx b ∧ dx uma = - dx uma ∧ dx b . Isto também assegura que o resultado do produto da cunha tem uma orientação.
Nós definimos o conjunto de todos estes produtos são de base 2- formas , e da mesma forma nós definimos o conjunto de produtos da forma dx uma ∧ dx b ∧ dx c ser básico 3- formas . Um geral K -forma é, em seguida, uma soma ponderada de base k- formas, em que os pesos são as funções lisa f . Juntas, estas formam um espaço vetorial com base k -forms como os vetores de base, e 0-formas (funções lisas) como o campo de escalares. O produto cunha, em seguida, estende-se k -forms de forma natural. Acima de R n na maioria dos n covectors pode ser linearmente independentes, assim, um k- forma com k > n será sempre zero, pela propriedade alternada.
Em adição ao produto de cunha, há também o exterior derivado operador d . Este mapas operador k -forms a ( k +1) -forms. Para um k ω -forma = f dx uma sobre R n , definimos a ação de d por:
com extensão para geralk-forms ocorrendo de forma linear.
Esta abordagem mais geral permite uma abordagem mais natural coordenar-se livre para integração em manifolds . Ele também permite uma generalização natural do teorema fundamental do cálculo , chamado de teorema de Stokes, que podemos afirmar como
onde ω é um geral K -forma, e ∂Ω denota a fronteira da região Ω. Assim, no caso em que ω é uma forma de 0 e Ω é um intervalo de fecho da linha real, isto reduz-se o teorema fundamental do cálculo . No caso em que é um ω-forma 1 e Ω é uma região 2-dimensional no avião, o teorema reduz a teorema de Green. Da mesma forma, usando 2-formas, e 3-formas e Hodge dualidade, podemos chegar a teorema de Stokes ea teorema da divergência. Desta forma, podemos ver que formas diferenciais fornecer uma poderosa visão unificadora da integração.
Os métodos e aplicações
Integrais de computação
A técnica mais básica para calcular integrais de uma variável real é baseado no teorema fundamental do cálculo . Ele prossegue assim:
- Escolha de uma funçãof(x) e um intervalo de [um,b].
- Encontrar uma primitiva def, isto é, uma funçãoFde modo a queF '=f.
- Pelo teorema fundamental do cálculo, desde o integrando e integral não têmsingularidades no caminho da integração,
- Por conseguinte, o valor do integral éF(b) -F(um).
Note-se que a integral não é, na verdade, a antiderivada, mas o teorema fundamental nos permite usar antiderivadas para avaliar integrais definidas.
A etapa é muitas vezes difícil encontrar uma antiderivada de f . Raramente é possível olhar para uma função e anote sua primitiva. Mais frequentemente, é necessário o uso de uma das muitas técnicas que foram desenvolvidas para avaliar integrais. A maioria destas técnicas reescrever uma integral como um diferente que é esperançosamente mais tratável. As técnicas incluem:
- Integração por substituição
- Integração por partes
- Integração por substituição trigonométrica
- Integração por frações parciais
- Integração por fórmulas de redução
Mesmo se estas técnicas falharem, pode ainda ser possível avaliar um determinado integrante. A próxima técnica mais comum é o cálculo de resíduos, enquanto que para integrais nonelementary série de Taylor , por vezes, pode ser usado para encontrar a antiderivada. Há também muitos menos comuns formas de calcular integrais definidas; por exemplo, identidade de Parseval pode ser usada para transformar uma integral sobre uma região retangular em uma soma infinita. Ocasionalmente, uma integral pode ser avaliada por um truque; para um exemplo disso, veja integrante Gaussian.
Cálculos de volumes desólidos de revolução pode ser feito normalmente coma integração de disco oua integração do escudo.
Os resultados específicos que foram trabalhados por várias técnicas são coletados nalista de integrais.
Algoritmos simbólicos
Muitos problemas de matemática, física e engenharia envolvem integração, onde uma fórmula explícita para a integral é desejado. Extenso tabelas de integrais foram compiladas e publicadas ao longo dos anos para esta finalidade. Com a disseminação da informática , muitos profissionais, educadores e estudantes têm se voltado para sistemas de álgebra computacional que são projetados especificamente para realizar tarefas difíceis ou tediosas, incluindo a integração. Integração simbólica apresenta um desafio especial para o desenvolvimento de tais sistemas.
Uma das maiores dificuldades na integração matemática simbólica é que, em muitos casos, uma fórmula fechada para a primitiva de uma função em vez inocente olhando simplesmente não existe. Por exemplo, sabe-se que as primitivas das funções exp ( x 2 ), x x e sin x / x não pode ser expressa sob a forma fechada envolvendo apenas racionais e exponenciais funções, logaritmo , trigonométrica e funções trigonométricas inversas, e as operações de multiplicação e composição; em outras palavras, nenhuma das três funções atribuídas é integrável na funções elementares. teoria de Galois Diferencial fornece critérios gerais que permitem determinar se o anti derivada de uma função primária é elementar. Infelizmente, verifica-se que as funções com expressões fechadas de antiderivadas são a excepção e não a regra. Consequentemente, os sistemas informatizados de álgebra não tem esperança de ser capaz de encontrar uma antiderivada de uma função elementar construído aleatoriamente. Do lado positivo, se os blocos de construção para antiderivadas são fixados com antecedência, pode ser ainda ser possível decidir se a antiderivada de uma determinada função pode ser expressa usando esses blocos e operações de multiplicação e composição, e para encontrar a resposta simbólica quando ela existe. O algoritmo Risch, implementado em Mathematica e os bordo sistemas de álgebra computacional, faz exatamente isso para funções e antiderivadas construídas a partir de funções racionais, radicais, logaritmo e funções exponenciais.
Alguns integrandos especiais ocorrem com freqüência suficiente para justificar um estudo especial. Em particular, pode ser útil dispor de, no conjunto de primitivas, as funções especiais de física (como as funções de Legendre, a função hipergeométrico, a função gama e assim por diante). Estendendo o algoritmo de Risch-Norman para que ele inclui estas funções é possível mas desafiador.
A maioria dos seres humanos não são capazes de integrar tais fórmulas gerais, portanto, em um sentido computadores são mais hábeis em integrar fórmulas altamente complicadas. Muito fórmulas complexas são susceptíveis de ter antiderivadas de forma fechada, assim como muito de uma vantagem faz este presente é uma questão filosófica que está aberto para debate.
Quadratura numérica
As integrais encontradas em um curso básico de cálculo são deliberadamente escolhido para simplicidade; aqueles encontrados em aplicações reais nem sempre são tão confortáveis. Algumas integrais não pode ser encontrado exatamente, alguns exigem funções especiais que são elas próprias um desafio para computar, e outros são tão complexas que encontrar a resposta exata é muito lento. Isso motiva o estudo ea aplicação de métodos numéricos para integrais de aproximação, que usam hoje flutuante aritmética de ponto electrónicos digitais em computadores . Muitas das idéias surgiram muito antes, para cálculos manuais; mas a velocidade de computadores de uso geral como o ENIAC criou uma necessidade de melhorias.
Os objetivos da integração numérica são precisão, confiabilidade, eficiência e generalidade. Métodos sofisticados podem vastamente superam um método ingênuo por todas as quatro medidas (Dahlquist & Björck próximas; Kahaner, Moler & Nash 1989; Stoer & Bulirsch 2002). Considere-se, por exemplo, o integral
que tem a resposta exata 94 / 25 = 3,76. (Na prática normal, a resposta não é conhecido antecipadamente, portanto, uma tarefa importante - não explorado por aqui -. É decidir quando uma aproximação é bom o suficiente) Um "livro de cálculo" abordagem divide o intervalo de integração em, digamos, 16 pedaços iguais, e calcula os valores da função.
Os valores da função espaçados x -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 f(x) 2,22800 2,45663 2,67200 2,32475 0,64400 -,92575 -,94000 -,16963 0,83600 x -1.75 -1.25 -0.75 -0.25 0,25 0,75 1,25 1.75 f(x) 2,33041 2,58562 2,62934 1,64019 -,32444 -1,09159 -,60387 0,31734
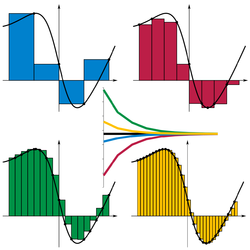
Usando a extremidade esquerda de cada pedaço, o método resume rectângulo 16 valores da função e multiplica pelo largura de passo, h , aqui 0,25, para obter um valor aproximado de 3,94325 para a integral. A precisão não é impressionante, mas o cálculo usa formalmente pedaços de largura infinitesimal, por isso inicialmente isto pode parecer pouco motivo para preocupação. Com efeito, dobrando repetidamente o número de etapas produz eventualmente uma aproximação de 3,76001. No entanto 2 18 são necessárias peças, uma grande despesa computacional para tão pouca precisão; e um alcance de maior precisão pode forçar passos tão pequenos que aritmética de precisão torna-se um obstáculo.
Uma abordagem melhor substitui os topos horizontais dos retângulos com topos inclinados tocar a função nas extremidades de cada peça. Este regra trapézio é quase tão fácil de calcular; que resume todos os valores de função 17, mas os pesos, a primeira e última por uma metade, e de novo multiplica por a largura passo. Isso melhora imediatamente à aproximação de 3,76925, o que é visivelmente mais precisa. Além disso, apenas duas 10 peças são necessários para atingir 3,76 mil, substancialmente menos do que o método de cálculo retângulo para uma precisão comparável.
O método de Romberg se baseia no método trapezoidal com grande efeito. Em primeiro lugar, os comprimentos do passo incremental são reduzidos para metade, dando aproximações trapezoidais denotados por T ( h 0 ), t ( h 1 ), e assim por diante, em que h k1 é a metade h k . Para cada novo tamanho do passo, apenas metade dos novos valores da função precisa ser calculado; os outros transitar do tamanho anterior (como mostrado na tabela acima). Mas a idéia é realmente poderoso para interpolar um polinômio através das aproximações, e extrapolar para T (0). Com este método um numericamente exata responder aqui requer apenas quatro peças (cinco valores de função)! O Lagrange polinomiais interpolação { h k , T ( h k )} k= 0 ... 2 = {(4.00,6.128), (2.00,4.352), (1.00,3.908)} é 3,76 + 0,148 h 2 , produzindo o valor extrapolado 3,76 em h = 0.
Quadratura de Gauss, muitas vezes requer visivelmente menos trabalho para precisão superior. Neste exemplo, ele pode calcular os valores da função em apenas dois x posições, ± 2 / √3 , em seguida, duas vezes cada valor e soma para obter a resposta numericamente exata. A explicação para este sucesso dramático encontra-se em análise de erros, e um pouco de sorte. Um n- método de Gauss ponto é exata para polinômios de grau até 2 n -1. A função neste exemplo é um grau polinomial 3, mais um termo que cancela porque os pontos finais escolhidas são simétricas em torno de zero. (Cancelamento também beneficia o método de Romberg.)
Mudando o intervalo deixou um pouco, para a integral é de -2,25 a 1,75, remove a simetria. No entanto, o método trapezoidal é bastante lento, o método de interpolação polinomial de Romberg é aceitável, e o método de Gauss requer o mínimo de trabalho - se o número de pontos é conhecida de antemão. Como assim, interpolação racional pode usar as mesmas avaliações trapezoidais como o método de Romberg para maior efeito.
Quadrature comparação de custos método Método Trapézio Romberg Racional Gauss Pontos 1048577 257 129 36 Rel. Err. -5,3 × 10-13 -6,3 × 10-15 8,8 × 10-15 3,1 × 10-15 Valor 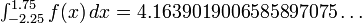
Na prática, cada método tem de utilizar avaliações adicionais para assegurar um limite de erro de uma função desconhecida; isso tende a compensar parte da vantagem do método de Gauss puro, e motiva do popular híbrido Gauss-Kronrod. Simetria ainda pode ser explorada por dividir essa integral em duas faixas, de -2,25 para -1,75 (sem simetria), e de -1,75 para 1,75 (simetria). Mais amplamente, quadratura adaptativa partições uma variedade em peças com base nas propriedades de função, de modo que os pontos de dados estão concentrados onde eles são mais necessários.
Esta breve introdução omite integrais de dimensão superior (por exemplo, área e cálculos de volume), onde as alternativas, tais comointegração Monte Carlo têm grande importância.
Um texto de cálculo é nenhum substituto para a análise numérica, mas o inverso também é verdadeiro. Mesmo o melhor código numérico adaptativo, por vezes, requer um usuário para ajudar com as integrais mais exigentes. Por exemplo, integrais impróprias pode exigir uma mudança de variáveis ou métodos que podem evitar os valores da função infinitas; e propriedades conhecidas como simetria e periodicidade pode constituir uma alavanca fundamental.

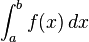
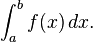
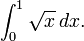
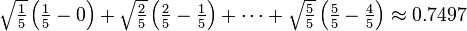
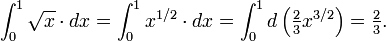
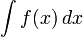
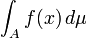
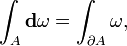
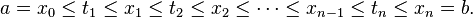
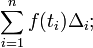
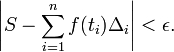
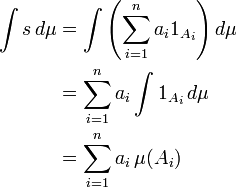
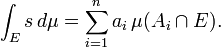
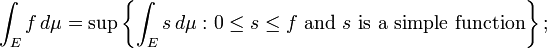

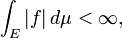
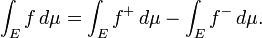
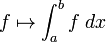
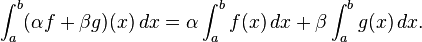
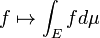
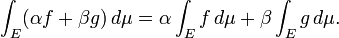
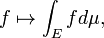
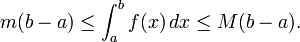
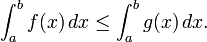
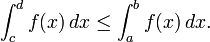
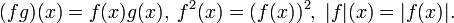
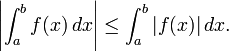
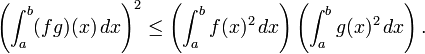
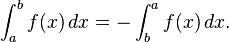
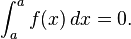
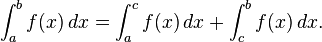
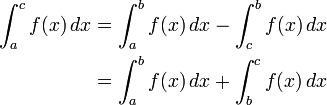
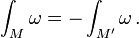
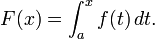
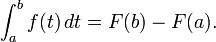
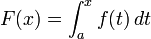

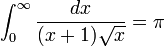
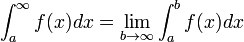
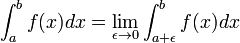
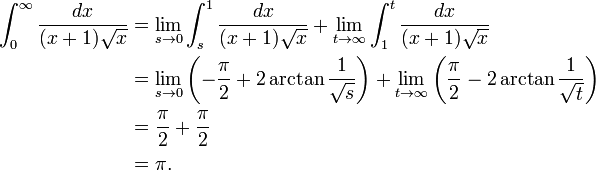
![\ Begin {align} \ int _ {- 1} ^ {1} \ frac {dx} {\ sqrt [3] {x ^ 2}} e {} = \ lim_ {s \ to 0} \ int _ {- 1} ^ {- s} \ frac {dx} {\ sqrt [3] {x ^ 2}} + \ lim_ {t \ to 0} \ int_ {t} ^ {1} \ frac {dx} {\ sqrt [3 ] {x ^ 2}} \\ & {} = \ lim_ {s \ to 0} 3 (1- \ sqrt [3] {s}) + \ lim_ {t \ to 0} 3 (1- \ sqrt [ 3] {t}) \\ & {} = 3 + 3 \\ & {} = 6. \ end {align}](../../images/116/11627.png)