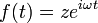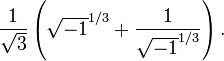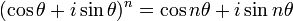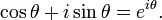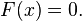Número complexo
Sobre este escolas selecção Wikipedia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...

Em matemática , um número complexo é um número que pode ser formalmente definido como um par ordenado de números reais (a, b), muitas vezes escritas:
onde i 2 = -1.
Os números complexos têm adição, subtração, multiplicação e divisão operações definidas, com comportamentos que são um super rigoroso dos números reais, bem como ter outras propriedades elegantes e úteis. Nomeadamente, os números negativos verdadeiros podem ser obtidas por quadratura números complexos.
Os números complexos foram inventados, quando se descobriu que a resolução de alguns equações cúbicas exigido cálculos intermediários contendo as raízes quadradas de números negativos, mesmo quando as soluções finais foram números reais. Além disso, a partir da teorema fundamental da álgebra, o uso de números complexos como o campo de número de polinomiais equações algébricas significa que as soluções sempre existe. O conjunto de números complexos formam um algebricamente fechado campo, em contraste com o conjunto de números reais, o que não é algebricamente fechado.
Os números complexos são usados em muitos campos diferentes, incluindo aplicações em engenharia , eletromagnetismo , física quântica , matemática aplicada e teoria do caos . Quando o campo subjacente de números para um tipo de matemática é o campo de números complexos, o nome geralmente reflete esse fato. São exemplos análise complexa, matriz complexa , polinomial complexo e álgebra de Lie complexa.
Definições
Notação
Embora outras notações pode ser usado, os números complexos são muitas vezes escrito na forma
em que a e b são números reais , e i é a unidade imaginária , que tem a propriedade de i 2 = -1. O número real a é chamado a parte real do número complexo, e o número real b é a parte imaginária .
Números reais podem ser expressos como números complexos, com a parte imaginária de zero; isto é, o número real a é equivalente ao número complexo a 0 i. Números complexos com parte real que é zero são chamados números imaginários.
Por exemplo, 3 + 2 i é um número complexo, com parte real e parte imaginária 3 2. Se z = a + ib, a parte real (a) é denotado Re (z) ou 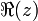 , E a parte imaginária (b) é denotada Im (z) ou
, E a parte imaginária (b) é denotada Im (z) ou 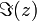 .
.
Em algumas disciplinas (em particular, engenharia elétrica , onde i é um símbolo para corrente), a unidade imaginária i é em vez escrito como j, portanto, os números complexos são por vezes escrito como uma JB +.

f (x) = (x-1 ²) (x -2- i) ² /
(X² + 2 + 2 i). A tonalidade representa o argumento de função, enquanto a saturação representa a magnitude.
O conjunto de todos os números complexos é normalmente indicado por C, ou em blackboard bold por 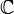 . Os números reais, r, pode ser considerado como um subconjunto de C, considerando cada número real como um complexo de: a = a + 0 i.
. Os números reais, r, pode ser considerado como um subconjunto de C, considerando cada número real como um complexo de: a = a + 0 i.
Igualdade
Dois números complexos são iguais se e somente se suas partes reais são iguais e suas partes imaginárias são iguais. Ou seja, a + bi = c + di se e somente se a = b = c e d.
Operações
Os números complexos são adicionados, subtraídos, multiplicados e divididos por aplicar formalmente a associativa , comutativa e leis distributivas da álgebra, em conjunto com a equação i 2 = -1:
- Adição:
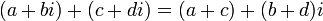
- Subtração:
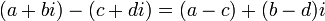
- Multiplicação:
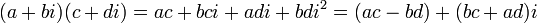
- Divisão:
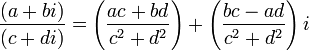
- Adição:
(Divisão de números complexos é ainda definido mais tarde).
O campo de números complexos
Formalmente, os números complexos pode ser definida como pares ordenados de números reais (a, b) em conjunto com as operações de:
Assim definido, os números complexos formam um campo, o campo número complexo, denotado por C (um campo é uma estrutura algébrica em que a adição, subtração, multiplicação e divisão são definidas e satisfazer certas leis algébricas. Por exemplo, os números reais formam um campo).
O número um verdadeiro é identificado com o número complexo (a, 0), e desta forma o campo de números reais R torna-se um subcampo de C. A unidade imaginária i pode, então, ser definido como o número complexo (0, 1), que verifica
Em C, temos:
- identidade aditivo ("zero"): (0, 0)
- identidade multiplicativo ("um"): (1, 0)
- inversa do aditivo (a, b): (- A, - b)
- multiplicativo inverso (recíproco) diferente de zero (a, b):
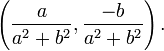
Uma vez que um número complexo a + bi é especificada exclusivamente por um par ordenado (a, b) de números reais, os números complexos são em um-para-um correspondência com os pontos num plano, o chamado plano complexo .
C também pode ser definida como a fecho topológico do números algébricos ou como o fecho algébrico de R, ambas as quais são descritas abaixo.
O plano complexo

 e seu conjugado
e seu conjugado  no plano complexo.
no plano complexo. Um número complexo z pode ser vista como um ponto ou um vector de posição num bidimensional sistema de coordenadas cartesianas, o chamado plano complexo ou Argand diagrama (nome Jean-Robert Argand) - ver figura à direita. O ponto e, portanto, o número complexo z pode ser especificado pelo cartesiana (retangular) coordena. As coordenadas cartesianas do número complexo são a parte real x = Re (z) e do imaginário parte y = Im (z). A representação de um número complexo pelas suas coordenadas cartesianas é chamado a forma cartesiano ou formato retangular ou algébrica do referido número complexo.
Valor absoluto, conjugação e distância
O valor absoluto (ou módulo ou magnitude) de um número complexo 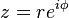 é definido como
é definido como 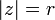 . Algebricamente, se
. Algebricamente, se 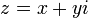 , Então
, Então 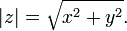
Pode-se verificar facilmente que o valor absoluto tem três propriedades importantes:
 se e apenas se
se e apenas se 
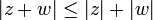 ( da desigualdade do triângulo)
( da desigualdade do triângulo)
para todos os números complexos z e w. Segue-se então, por exemplo, que 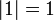 e
e  . Ao definir a função distância
. Ao definir a função distância 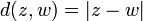 voltamo-nos o conjunto dos números complexos em um espaço métrico e, portanto, podemos falar de limites e continuidade.
voltamo-nos o conjunto dos números complexos em um espaço métrico e, portanto, podemos falar de limites e continuidade.
O conjugado complexo do número complexo 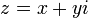 é definido como sendo
é definido como sendo 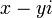 , Como escrito
, Como escrito 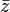 ou
ou 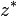 . Como pode ser visto na figura,
. Como pode ser visto na figura, 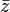 é o "reflexo" de z sobre o eixo real. O seguinte pode ser verificado:
é o "reflexo" de z sobre o eixo real. O seguinte pode ser verificado:
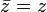 Se e apenas se z é real
Se e apenas se z é real
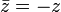 Se e apenas se z é puramente imaginário
Se e apenas se z é puramente imaginário
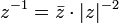 Se z é diferente de zero.
Se z é diferente de zero.
A última fórmula é o método de escolha para calcular o inverso de um número complexo se for dado em coordenadas rectangulares.
Que os deslocamentos de conjugação com todas as operações algébricas (e muitas funções; por exemplo, 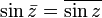 ) Está enraizada na ambiguidade na escolha de i (-1 tem duas raízes quadradas). É importante notar, no entanto, que a função
) Está enraizada na ambiguidade na escolha de i (-1 tem duas raízes quadradas). É importante notar, no entanto, que a função 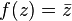 não é complexa-diferenciável (veja função holomorfa).
não é complexa-diferenciável (veja função holomorfa).
Fracções complexas
Podemos dividir um número complexo (a + bi) por outro número complexo (c + di) ≠ 0 em duas maneiras. A primeira maneira já foi implicado: para converter os dois números complexos na forma exponencial, a partir do qual o seu quociente é facilmente derivada. A segunda maneira consiste em expressar a divisão como uma fracção, em seguida, para multiplicar o numerador e denominador pelo conjugado complexo do denominador. O novo denominador é um número real.
Interpretação geométrica das operações com números complexos



Considere um avião . Um ponto é a origem, 0. Outro ponto é a unidade, ou 1.
A soma dos dois pontos A e B é o ponto X = A + B de tal modo que os triângulos com vértices 0, A, B, e X, B, A, estão congruentes.
O produto de dois pontos A e B é o ponto X = AB de tal modo que os vértices de triângulos com 0, 1, A e 0, B, X, são semelhante.
O conjugado complexo de um ponto A é o ponto X = A * tal que os triângulos com vértices 0, 1, A e 0, 1, X, são imagens de espelho um do outro.
Esta interpretação geométrica permite que os problemas de geometria a ser traduzido para álgebra. O problema da construção geométrica do 17-gon é, portanto, traduzida para a análise da equação algébrica x 17 = 1.
Forma polar
Como alternativa para a representação cartesiana z = x + iy, o número complexo z pode ser especificado por coordenadas polares . As coordenadas polares são r = | z | ≥ 0, chamado de valor absoluto ou módulo, e φ = arg (z), chamou o argumento ou o ângulo de z. Para r = 0 qualquer valor de φ descreve o mesmo número. Para se ter uma representação única, uma escolha convencional é definir arg (0) = 0. Para r> 0 o argumento φ é único módulo 2π; isto é, se todos os dois valores do argumento complexo diferem por um valor exacto número inteiro múltiplo de 2π, eles são considerados equivalentes. Para se ter uma representação única, uma escolha convencional é limitar φ para o intervalo (-π, π], ou seja, -π <φ ≤ π. A representação de um número complexo pelas suas coordenadas polares é chamada a forma polar do número complexo .
Conversão de forma polar à forma cartesiana
Conversão da forma cartesiana para a forma polar
(Ver função arg e atan2.)
O valor resultante para φ está na gama (-π, π +];. É negativa para valores negativos de y Se os valores não-negativos, em vez no intervalo [0, 2π) são desejados, adicionar 2π a resultados negativos.
Notação da forma polar
A notação da forma polar como
é chamado de forma trigonométrica. O φ notação cis às vezes é usado como uma abreviação para cos φ + i sin φ. Uso Fórmula de Euler que também pode ser escrito como
que é chamado de forma exponencial.
Multiplicação, divisão, exponenciação, e extração de raiz na forma polar
Multiplicação, divisão, exponenciação, e extração de raiz são muito mais fáceis na forma polar do que na forma cartesiana.
Uso soma e diferença identidades sua possível obter que
e essa
Exponenciação com expoentes inteiros; conforme A fórmula de De Moivre,
Exponenciação com expoentes complexos arbitrários é discutido no artigo sobre exponenciação .
A adição de dois números complexos é apenas a adição de vectores de dois vectores, e a multiplicação por um número complexo fixo pode ser visto como uma rotação simultânea e alongamento.
Multiplicação por i corresponde a uma rotação anti-horário em 90 graus (π / 2 radianos ). O conteúdo geométrica da equação i 2 = -1 é que uma sequência de dois resultados de rotações de 90 graus em grau 180 (π radianos) rotação. Mesmo o fato (-1) · (-1) = 1 dos aritmética podem ser entendido geometricamente como a combinação de dois gira 180 graus.
Todas as raízes de qualquer número, real ou complexo, pode ser encontrado com um simples algoritmo . O n-ésimo raízes são dadas por
para k = 0, 1, 2, ..., N - 1, onde ![\ Sqrt [n] {r}](../../images/145/14548.png) representa o principal n º raiz de r.
representa o principal n º raiz de r.
Algumas propriedades
Representação matriz de números complexos
Embora geralmente não é útil, representações alternativas do campo complexo pode dar alguns insights sobre sua natureza. Uma representação particularmente elegante interpreta cada número complexo como um 2 × 2 da matriz com reais entradas que se estende e gira os pontos do plano. Toda essa matriz tem a forma
em que a e b são números reais. A soma eo produto de duas dessas matrizes é novamente desta forma, ea operação do produto em matrizes desta forma é comutativa . Cada matriz diferente de zero desta forma é invertida, e seu inverso é novamente desta forma. Portanto, as matrizes de esta forma são uma campo, isomorfo para o campo de números complexos. Cada tal matriz pode ser escrita como
o que sugere que nós devemos identificar o real número 1 com a matriz de identidade
e a unidade imaginária i com
uma rotação anti-horário em 90 graus. Note-se que o quadrado desta última matriz é de facto igual ao da matriz 2 x 2 que representa -1.
O quadrado do valor absoluto de um número complexo expresso como uma matriz é igual ao determinante da matriz que.
Se a matriz é visto como uma transformação do plano, em seguida, a transformação gira pontos por meio de um ângulo igual ao argumento do número complexo e escalas por um factor igual ao valor absoluto do número complexo. O conjugado do número complexo z corresponde à transformação que gira através do mesmo ângulo que Z, mas no sentido oposto, e dimensiona, da mesma maneira como Z; isto pode ser representado pela transposição da matriz correspondente a z.
Se os elementos de matriz são eles mesmos números complexos, o que é resultante de álgebra do quaternions. Em outras palavras, esta representação matricial é uma forma de expressar a Cayley-Dickson construção de álgebras.
Deve também ser notado que os dois valores próprios da matriz de 2x2 que representam um número complexo são o próprio número complexo e do seu conjugado.
Espaço vetorial real
C é uma verdadeira bidimensional de espaço vectorial . Ao contrário dos reais, o conjunto dos números complexos não pode ser totalmente ordenados em qualquer forma que seja compatível com as suas operações aritméticas: C não pode ser transformado em um campo ordenada. Mais geralmente, nenhum campo contendo uma raiz quadrada de -1 pode ser encomendado.
Mapas -linear R C → C tem a forma geral
com coeficientes complexos a e b. Apenas o primeiro termo é -linear C, e apenas o primeiro termo é holomorphic; o segundo termo é real-diferenciáveis, mas não satisfaz a Equações de Cauchy-Riemann.
A função
corresponde a rotações combinadas com escala, enquanto que a função
corresponde a reflexões combinados com raspagem.
Soluções de equações polinomiais
A raiz do polinômio p é um número complexo z tal que p (z) = 0. Um resultado surpreendente em análise complexa é que todos os polinômios de grau n com coeficientes reais ou complexos têm raízes exatamente n complexos (contagem múltiplas raízes de acordo com a sua multiplicidade). Isto é conhecido como o teorema fundamental da álgebra, e isso mostra que os números complexos são uma corpo algebricamente fechado.
De facto, o campo do número complexo C é a fecho algébrico do campo do número real, e Cauchy construído o campo de números complexos desta maneira. Ele também pode ser caracterizada como a anel quociente do polinômio anel R [X] sobre a ideal gerado pelo polinômio X ² + 1:
Este é realmente um campo porque X ² + 1 é irredutível, gerando, portanto, uma ideal maximal, em R [X]. A imagem de X neste anel quociente é a unidade imaginária i.
Caracterização algébrica
O domínio C é ( -se ao campo isomorfismo) caracterizado pelos factos seguintes três:
- sua característica é 0
- sua grau de transcendência através da campo principal é a cardinalidade do continuum
- é algebricamente fechado
Consequentemente, C contém muitos subcampos adequados que são isomorfos a C. Outra consequência desta caracterização é que o Grupo de Galois de C sobre os números racionais é enorme, com cardinalidade igual o do conjunto do continuum de energia.
Caracterização como um campo topológico
Como observado acima, a caracterização algébrica de C não consegue captar algumas das suas propriedades mais importantes. Essas propriedades, que sustentam os fundamentos da análise complexa, surgem a partir da topologia de C. As seguintes propriedades caracterizar C como um campo topológico:
- C é um campo.
- C contém um subconjunto de elementos diferentes de zero P satisfatórios:
- P é fechado sob adição, multiplicação e tomando inversas.
- Se X e Y são elementos distintos de P, em seguida, XY ou yx é em P
- Se S é qualquer subconjunto não vazio de P, então S + P = x + P para algum x em C.
- C tem um automorphism involutiva não trivial x → x *, que fixa P e tal que xx * está em P para quaisquer x diferentes de zero em C.
Dadas estas propriedades, pode-se, em seguida, definir uma topologia em C, tendo os conjuntos
como uma base, onde x varia ao longo C, e p varia ao longo do P.
Para ver de que essas propriedades caracterizar C como um campo topológico, nota-se que P ∪ {0} ∪ -P é um ordenado Dedekind-campo completo e, portanto, pode ser identificado com o número verdadeiro R por um isomorfismo campo exclusivo. A última propriedade é facilmente visto implicar que a Grupo de Galois sobre os números reais é de ordem dois, completando a caracterização.
Pontryagin mostrou que a única conectado localmente compacto campos topológicos são R e C. Isto dá uma outra caracterização de C, como um campo topológico, uma vez que C pode ser distinguida de R notando que os números complexos são diferentes de zero ligado, enquanto os números reais diferentes de zero não são.
Análise Complexa
O estudo das funções de uma variável complexa é conhecido como análise complexa e tem um enorme utilidade prática em matemática aplicada , bem como em outros ramos da matemática. Muitas vezes, as provas mais naturais para declarações em análise real ou mesmo a teoria dos números empregar técnicas de análise complexa (ver teorema de número primo para um exemplo). Ao contrário das funções reais que são comumente representados como dois gráficos tridimensionais, funções complexas tem quatro gráficos tridimensionais e podem ser utilmente ilustrado por cor codificação de um três gráfico tridimensional para sugerir quatro dimensões, ou por transformação animar dinâmica da função complexa do plano complexo.
Aplicações
As palavras "reais" e "imaginários" foram significativas quando os números complexos foram usados principalmente como uma ajuda na manipulação de números "reais", com apenas a parte "real", descrevendo diretamente o mundo. Aplicações posteriores, e especialmente a descoberta da mecânica quântica, mostrou que a natureza não tem preferência por números "reais" e suas descrições mais real muitas vezes exigem números complexos, a parte "imaginário" ser tão física como a parte "real".
Teoria de controle
Na teoria de controle , sistemas são muitas vezes transformada a partir da domínio do tempo para o domínio da freqüência usando o Laplace. O sistema pólos e zeros são então analisados no plano complexo. O lugar das raízes, Nyquist enredo, e Técnicas de plotagem Nichols todos fazem uso do plano complexo.
No método lugar geométrico das raízes, é especialmente importante se o pólos e zeros estão nos planos meia esquerda ou direita, ou seja, ter verdadeira parte maior ou menor do que zero. Se um sistema tem pólos que são
- no semi-plano direito, será instável,
- tudo no semi-plano esquerdo, será estável,
- no eixo imaginário, que terá estabilidade marginal.
Se um sistema tem zeros no semi-plano direito, é um sistema de fase nonminimum.
Análise de sinais
Os números complexos são utilizados em análise de sinais e outros campos para obter uma descrição conveniente para sinais variáveis periodicamente. Para dadas funções reais que representam quantidades físicas reais, muitas vezes em termos de senos e co-senos, correspondentes funções complexas são consideradas de que as partes reais são as quantidades originais. Para onda seno de um dado frequência, o valor absoluto | z | z do correspondente é o amplitude e o argumento arg (z) o fase.
Se A análise de Fourier é empregado para escrever um dado sinal de valor real como uma soma de funções periódicas, estas funções periódicas são muitas vezes escritos como funções complexas valorizado da forma
onde representa a ω frequência angular e do número complexo z codifica a fase e amplitude como explicado acima.
Em engenharia elétrica , a Transformada de Fourier é utilizado para analisar variando e tensões correntes. O tratamento de resistores, capacitores, e indutores pode então ser unificados através da introdução, resistências dependentes da freqüência imaginários para os dois últimos e combinando todos os três em um único número complexo chamado a impedância. (Engenheiros elétricos e alguns físicos usam a letra j para a unidade imaginária desde que eu é normalmente reservado para as correntes variadas e podem entrar em conflito com i.) Esta abordagem é chamada cálculo fasorial. Esse uso também é estendido para processamento de sinal digital e processamento de imagens digitais que utilizam versões digitais de análise de Fourier (e Análise Wavelet) para transmitir, comprimir, restaurar e caso contrário processo digitais de áudio sinais, imagens fixas e os sinais de vídeo.
Integrais impróprias
Em áreas aplicadas, os números complexos são frequentemente utilizados para calcular determinado valor de reais integrais impróprias, por meio de funções complexas de valor. Existem vários métodos para fazer isso; ver métodos de integração de contorno.
Mecânica quântica
O campo de número complexo é relevante no formulação matemática da mecânica quântica, onde complexo Espaços de Hilbert fornecer o contexto para uma tal formulação que seja conveniente e talvez o mais padrão. As fórmulas originais de fundação da mecânica quântica - o Schrödinger e equação Heisenberg mecânica matricial - fazer uso de números complexos.
Relatividade
Em especial e relatividade geral , algumas fórmulas para a métrica no o espaço-tempo se tornam mais simples se tivermos a variável tempo para ser imaginário. (Isto já não é padrão.) Os números complexos são essenciais para espinores que são uma generalização do tensores usados na relatividade.
Matemática aplicada
Em equações diferenciais , é comum a primeira a encontrar todos os complexos raízes r do característica de uma equação equação diferencial linear e, em seguida, tentar resolver o sistema em termos de funções de base da forma f (t) = e rt.
Dinâmica de fluidos
Em dinâmica de fluidos, funções complexas são usados para descrever potencial de fluxo em duas dimensões.
Fractals
Certos fractais são traçados no plano complexo por exemplo, conjunto de Mandelbrot e Julia definido.
História
A mais antiga referência fugaz ao quadrado raízes de números negativos talvez ocorreu na obra do grego matemático e inventor Heron de Alexandria, no século 1 dC , quando considerado o volume de um impossível tronco de uma pirâmide , embora os números negativos não foram concebidos no Mundo helênico.
Os números complexos tornou-se mais proeminente no século 16 , quando fechado fórmulas para as raízes de e cúbico quárticas polinômios foram descobertos por matemáticos italianos (ver Niccolo Fontana Tartaglia, Gerolamo Cardano). Ele logo percebeu que estas fórmulas, mesmo se um só estava interessado em soluções reais, por vezes necessária a manipulação de raízes quadradas de números negativos. Por exemplo, a fórmula cúbico de Tartaglia dá a seguinte solução para a equação x ³ - x = 0:
À primeira vista, isso parece absurdo. No entanto cálculos formais com números complexos mostram que a equação z = 3 i tem soluções -i, 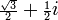 e
e 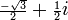 . Substituindo estes por sua vez para
. Substituindo estes por sua vez para 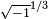 na fórmula cúbico de Tartaglia e simplificando, obtém-se 0, 1 e -1 como as soluções de 3 x - x = 0.
na fórmula cúbico de Tartaglia e simplificando, obtém-se 0, 1 e -1 como as soluções de 3 x - x = 0.
Este foi duplamente preocupante uma vez que nem mesmo os números negativos foram consideradas em terra firme na época. O termo "imaginário" para estas quantidades foi cunhado por René Descartes em 1637 e foi concebido para ser pejorativo (veja número imaginário para uma discussão sobre a "realidade" dos números complexos). Uma outra fonte de confusão foi que a equação 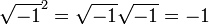 parecia ser caprichosamente incompatível com a identidade algébrica
parecia ser caprichosamente incompatível com a identidade algébrica 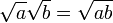 , O que é válido para positivo números reais e b, e que também foi utilizado em cálculos com números complexos com um de a, b positivo e outro negativo. O uso incorreto desta identidade (e da identidade relacionados
, O que é válido para positivo números reais e b, e que também foi utilizado em cálculos com números complexos com um de a, b positivo e outro negativo. O uso incorreto desta identidade (e da identidade relacionados 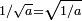 ) No caso em que tanto a como b são negativos, mesmo bedeviled Euler . Esta dificuldade levou à convenção de usar o símbolo especial i no lugar de
) No caso em que tanto a como b são negativos, mesmo bedeviled Euler . Esta dificuldade levou à convenção de usar o símbolo especial i no lugar de 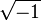 para se proteger contra este erro.
para se proteger contra este erro.
O século 18 viu o trabalho dos Abraham de Moivre e Leonhard Euler . Para Moivre é devido (1730) a fórmula bem conhecida que leva seu nome, A fórmula de de Moivre:
e Euler (1748) Fórmula de Euler análise complexa:
A existência de números complexos não foi completamente aceite até que a interpretação geométrica (ver abaixo) foi descrita pela Caspar Wessel em 1799 ; foi redescoberto vários anos mais tarde e popularizado por Carl Friedrich Gauss , e como resultado, a teoria dos números complexos recebeu uma notável expansão. A idéia da representação gráfica dos números complexos tinha aparecido, no entanto, já em 1685, em De Algebra tractatus de Wallis.
Memórias de Wessel apareceu na revista Proceedings, da Copenhagen Academy para 1799, e é extremamente clara e completa, mesmo em comparação com obras modernas. Ele também considera a esfera, e dá um quaternion teoria a partir do qual ele desenvolve uma trigonometria esférica completa. Em 1804 o Abbé buée veio de forma independente sobre a mesma idéia que Wallis tinha sugerido, que 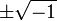 deve representar uma unidade de linha, e o seu negativo, perpendicular ao eixo real. Papel de buée não foi publicado até 1806, ano em que Jean-Robert Argand também emitiu um folheto sobre o mesmo assunto. É para o ensaio de Argand que a base científica para a representação gráfica dos números complexos é agora geralmente referidos. No entanto, em 1831, Gauss descobriu a teoria completamente desconhecido, e em 1832 publicou seu livro de memórias chefe sobre o assunto, trazendo-o, assim, de forma destacada antes que o mundo matemático. Menção também deve ser feita de um excelente pequeno tratado por Mourey (1828), em que as bases para a teoria dos números direcionais são cientificamente estabelecidas. A aceitação geral da teoria não é um pouco devido aos trabalhos de Augustin Louis Cauchy e Niels Henrik Abel, e especialmente o último, que foi o primeiro a usar corajosamente números complexos com um sucesso que é bem conhecido.
deve representar uma unidade de linha, e o seu negativo, perpendicular ao eixo real. Papel de buée não foi publicado até 1806, ano em que Jean-Robert Argand também emitiu um folheto sobre o mesmo assunto. É para o ensaio de Argand que a base científica para a representação gráfica dos números complexos é agora geralmente referidos. No entanto, em 1831, Gauss descobriu a teoria completamente desconhecido, e em 1832 publicou seu livro de memórias chefe sobre o assunto, trazendo-o, assim, de forma destacada antes que o mundo matemático. Menção também deve ser feita de um excelente pequeno tratado por Mourey (1828), em que as bases para a teoria dos números direcionais são cientificamente estabelecidas. A aceitação geral da teoria não é um pouco devido aos trabalhos de Augustin Louis Cauchy e Niels Henrik Abel, e especialmente o último, que foi o primeiro a usar corajosamente números complexos com um sucesso que é bem conhecido.
Os termos comuns usados na teoria são principalmente devido a seus fundadores. Argand chamado 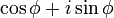 o factor de direcção, e
o factor de direcção, e 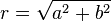 o módulo; Cauchy (1828) chamado
o módulo; Cauchy (1828) chamado 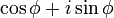 a forma reduzida (l'expressão réduite); Gauss usado para i
a forma reduzida (l'expressão réduite); Gauss usado para i 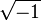 , Introduziu o número complexo prazo para
, Introduziu o número complexo prazo para 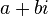 E chamado
E chamado 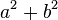 a norma.
a norma.
O coeficiente de direção expressão, muitas vezes utilizados para 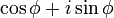 , É devido a Hankel (1867), eo valor absoluto, para o módulo, é devido a Weierstrass.
, É devido a Hankel (1867), eo valor absoluto, para o módulo, é devido a Weierstrass.
Na sequência de Cauchy e Gauss já percorreu um número de contribuintes de alto escalão, de quem o seguinte pode ser especialmente mencionados: Kummer (1844), Leopold Kronecker (1845), Scheffler (1845, 1851, 1880), Bellavitis (1835, 1852), Peacock (1845), e De Morgan (1849). Möbius também deve ser mencionado por suas inúmeras memórias sobre as aplicações geométricas de números complexos, e Dirichlet para a expansão da teoria para incluir números primos, congruencias, reciprocidade, etc., como no caso de números reais.
Um complexo anel ou campo é um conjunto de números complexos que é fechado sob adição, subtração, e multiplicação. Gauss estudou números complexos da forma 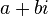 , Onde a e b são integrais, ou racional (e i é uma das duas raízes de
, Onde a e b são integrais, ou racional (e i é uma das duas raízes de  ). Seu aluno, Ferdinand Eisenstein, estudou o tipo
). Seu aluno, Ferdinand Eisenstein, estudou o tipo 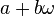 , Onde
, Onde 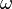 é uma raiz complexa de
é uma raiz complexa de  . Outros tais classes (chamados campos ciclotômicos) de números complexos são derivados da raízes da unidade
. Outros tais classes (chamados campos ciclotômicos) de números complexos são derivados da raízes da unidade 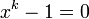 para valores mais elevados de
para valores mais elevados de  . Esta generalização é em grande parte devido à Kummer, que também inventou números ideais, que foram expressas como entidades geométricas por Felix Klein em 1893. A teoria geral dos campos foi criado por Évariste Galois, que estudou os campos gerados pelas raízes de qualquer equação polinomial
. Esta generalização é em grande parte devido à Kummer, que também inventou números ideais, que foram expressas como entidades geométricas por Felix Klein em 1893. A teoria geral dos campos foi criado por Évariste Galois, que estudou os campos gerados pelas raízes de qualquer equação polinomial
Os escritores final (de 1884) sobre a teoria geral incluem Weierstrass, Schwarz, Richard Dedekind, Otto Hölder, Bonaventure Berloty, Henri Poincaré, Estudo Eduard, e Alexander MacFarlane.
A definição formalmente correto usando pares de números reais foi dado no século 19 .



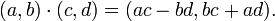
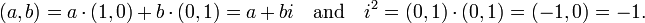
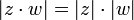
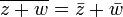
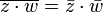
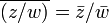
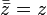
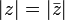
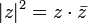
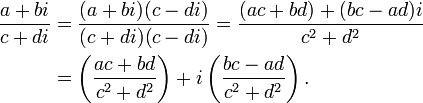
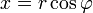

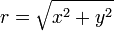
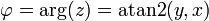
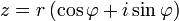
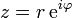

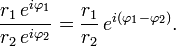
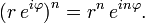
![\ Sqrt [n] {re ^ {i \ varphi}} = \ sqrt [n] {r} \ e ^ {i \ left (\ frac {\ varphi + 2k \ pi} {n} \ right)}](../../images/145/14547.png)
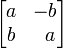
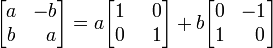
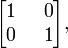


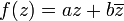
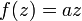
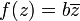
![\ Mathbb {C} = \ mathbb {R} [X] / (X ^ 2 + 1). \,](../../images/145/14557.png)